基于深度学习网络的异步电动机故障识别
2023-01-30王彪戴毓
王彪, 戴毓
(湖南石油化工职业技术学院,机电工程学院, 湖南,岳阳 414000)
0 引言
异步电动机也称为感应电动机,运行效率低是其一个显著的特点,并且,该电机的成本较低、组成结构不复杂,因此,其多用于粉碎机、压缩机等方面。定子和转子是异步电动机的主要部件,两者之间仅存在较小的间隙,如果电动机的工作环境和运行条件较为复杂和恶劣,对于异步电动机的运行可靠性和稳定性会造成较大影响,严重则会导致异步电动机发生机械故障,降低机电设备的使用寿命,并且影响工业生产。因此,识别异步电动机运行故障是保证工业生产、延长异步电动机的使用寿命的重要手段[1]。深度学习网络(DNN)是一种应用较为广泛的多层无监督神经网络学习方法,具有无监督训练的特点,在目标识别领域中具有良好的应用效果。
针对异步电动机故障识别问题,郑晓亮等[2]研究基于谐波分析的异步电动机故障识别方法,该方法通过对采集的电流信号实行去噪和频谱分析后,获取其高次谐波,将归一化后的谐波和劣化标准作比对,完成故障识别;其在识别过程中,抗噪性能较差;林志芳[3]研究基于CCF-HTLS算法的异步电动机故障识别方法,该方法对采集的电流信号实行预处理后,为提升识别精度,采用逆同步旋转消除基波后,通过相关函数技术对电流中的高斯有色噪声实行处理后,完成识别,但是该方法的故障频率偏移较高。因此,本文提出基于深度学习网络的异步电动机故障识别方法,准确完成异步电动机故障识别。
1 基于深度学习网络的异步电动机故障识别方法
1.1 异步电动机故障特征提取
1.1.1 异步电动机故障特征提取的降噪自编码网络
本文针对异步电动机故障识别需求,采用深度学习网络进行故障识别,采用降噪自编码网络(DAE)结构模型完成。由于该网络是深度学习网络中的典型网络,对于数据中的分布式特征提取具有显著的优势。异步电动机在故障识别过程中,则需依据传感器采集到的异步电动机故障信号数据完成,因此,本文采用DAE模型对异步电动机运行数据实行特征提取,该模型的结构如图1所示。

图1 降噪自编码网络结构
DAE模型能够获取异步电动机运行数据中的分布式特征,并且能够刻画数据中的高层特征,该刻画是通过低层特征组合完成。整个模型可分为两个部分,分别是编码和解码,编码的主要作用是对输入模型中的传感器采集的异步电动机运行数据实行编码;解码的主要作用是获取数据中有效的、没有噪声干扰的、能够描述异步电动机运行状态的数据,以此保证特征提取的可靠性。
设{x1,…,xm,…,xM}为传感器采集的异步电动机运行数据[4],将其作为DAE的输入,其中,M表示数据总量,m表示第m个数据;模型的输出用{z1,…,zm,…,zM}表示。模型的损失函数计算公式为
(1)
DAE模型在进行数据编码过程中,输入的数据是上一个自编码结构的编码层的结果,则编码层输出数据的计算公式为
(2)
DAE模型在解码过程中,对ym实行重构[5],以此获取没有噪声的数据zm,重构公式为
zm=sg(W′ym+d)
(3)
式中,sg和g均表示函数,前者为响应,后者为激活;连接权重用W′表示。
结合上述公式可知,DAE模型在学习训练过程中,无需依据其他参数和标签,依据输入数据和重构数据之间的误差即可获取编码结构的W和b。
为提升DAE模型对于异步电动机运行数据中分布式特征的提取效果,在DAE模型的L(xm,zm)中引入稀疏性惩罚因子λ,对其实行优化形成稀疏DAE模型,该模型的L(xm,zm)计算公式为
(4)
优化后的稀疏DAE模型具有显著的聚类能力,能够充分获取并利用采集的异步电动机运行数据中的有效数据,并提取数据中描述异步电动机运行状态的分布式特征,为故障识别提供可靠依据。
1.1.2 特征提取的稀疏DAE模型优化
依据上述1.1.1小节形成稀疏DAE模型后,为了提升稀疏DAE模型的表达能力,进一步保证特征提取效果,采用依次堆叠的方式对DAE模型实行处理,依次获取深度网络结构,即为叠降噪自编码器(SDAE)[6-7],SDAE通过预训练和微调两个部分,完成异步电动机故障特征提取,其结构如图2所示。

图2 叠降噪自编码器结构
DAE模型经过堆叠处理后,通过贪婪训练获取异步电动机故障特征提取结果。并且,为实现SDAE整体最优,需对带有异步电动机运行状态标签的数据样本进行监督训练,以此完成SDAE的微调,文中采用BP算法实现。
1.2 异步电动机故障识别实现
依据SDAE完成异步电动机运行状态特征提取后,将提取的分布式特征结果输入多响应线性回归模型中,该模型对该特征实行集成决策后,完成异步电动机故障识别[8-9]。

(5)
式(5)中,PCi(x(m))表示Ci对x(m)决策的概率,P(x(m))表示列向量,其维数为一个c×L,该向量的计算公式为
(6)
多响应线性回归模型在进行异步电动机故障识别时,能够将包含异步电动机故障类别c的分类问题实行转化,形成包含c个异步电动机故障类别回归问题。
将上述获取的异步电动运行特征x(m)属于故障类yj的PCi(x(m))结果作为输入特征,以此构建多响应线性回归模型[9]。通过该模型对故障识别问题实行转换,形成对应于故障类别yj的回归问题;以此,判断异步电动机的故障结果。如果输出的异步电动机故障类别标签位于个体中,其结果等于1。反之结果等于0[10]。因此,异步电动机的故障类别yj计算公式为
(7)
式中,LRj[ ]表示线性回归函数,α表示模型参数。
求解式(7),求解结果即为异步电动机被决策为LRj[x(m)]的类,并且,计算结果的最大值即为异步电动机故障类别识别结果,其公式为
(8)
2 测试结果与分析
采用型号为Y280S-2,额定功率功率为15 kW,额定电压为220 V,电流为5 A,额定转速为500(r/min)的三相异步电动机作为实例测试对象,并构建实验台,模拟三相异步电动机在运行时的5种故障情况,故障1至故障5分别为应匝间短路、相间短路、电机损坏、转轴磨损、端盖损坏。
采用本文方法在进行异步电动机故障识别时,需先确定深度网络模型的最佳隐含层数量和神经元数量。在不同隐含层数量和不同神经元数量下,本文方法对异步电动机的故障识别结果,如图3、图4所示。

图3 隐含层层数对识别准确准确率的影响
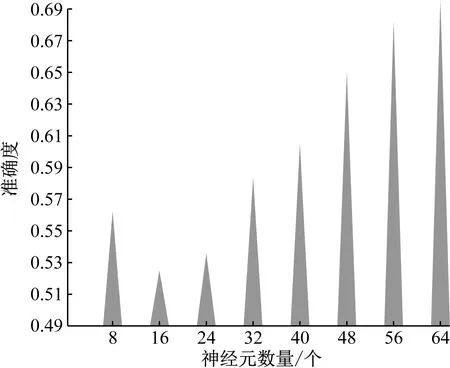
图4 神经元数量对识别准确率的影响
根据图3、图4的测试结果可知:随着隐含层层数和神经元数量的逐渐增加,本文方法对异步电动机的故障识别准确率也逐渐提高,当层数达到5层以上后,准确率的变化幅度逐渐降低,准确率结果达到0.96左右;并且,神经元的数量达到56个以后,准确率的变化幅度较小,其准确率结果达到0.69左右。因此,结合实际应用需求,在保证故障识别可靠性、且降低运行复杂程度的前提下,确定隐含层数量为5,神经元数量为64,用于后续实验中。
为验证本文方法的特征提取性能,将本文方法的特征提取结果与文献[2]的基于谐波分析的异步电动机故障诊断方法和文献[3]的基于CCF-HTLS算法的异步电动机故障识别方法提取的特征结果作对比,结果如表1所示。

表1 3种方法的对比结果 单位:ms
根据表1的测试结果可知:本文方法在测试集上的分类正确率为95.88%,并且寻优时间为1 939 ms,2种对比方法的测试集分类正确率均低于本文方法,并且寻优时间明显多于本文方法,说明本文方法可快速、有效完成故障特征提取和寻优。
为验证本文方法故障识别的有效性,对比3种方法在不同信噪比情况下的故障识别结果,如图5所示。信噪比越高表示噪声越小。

图5 3种方法的识别对比结果
分析图5的测试结果可知:随着信噪比的逐渐减小,3种方法的识别准确率均产生不同程度的下降。但是本文方法在信噪比范围在0~-15 dB内时,依旧可保证较高的识别率,但是两种对比方法只在信噪比在5~15 dB范围内的识别率在80%左右,在信噪比范围在0~-15 dB内时识别率却大幅度下降。因此说明本文方法具备较好的抗噪性能以及较高的稳定性。
为判断本文方法的识别优劣,选用故障频率偏移指标作为衡量标准,测试3种方法针对5种故障的故障频率偏移,结果如图6所示。

图6 3种方法的故障频率偏移结果
根据图6的测试结果可知:本文方法的最高故障频率偏移为0.058 Hz,最低故障频率偏移为0.012 Hz,2种对比方法的故障频率偏移则显著高于本文方法,说明本文方法的识别性能优于两种对比方法,可在故障频率偏移较小的情况下完成故障的准确识别。
3 总结
为了准确、实时识别异步电动机故障,本文提出了深度学习网络的异步电动机故障识别方法,该方法采用2个步骤完成,分别是异步电动机故障特征提取和异步电动机故障识别。测试结果表明:本文所提方法的应用性能良好,能够有效提取异步电动机运行数据中的分布式特征,精准识别异步电动机故障,并且抗噪性能较好,故障偏移结果较小。
