算筹之筹——从计算之物看计算之变

陈凯 上海市位育中学

《周易·系辞》说：“天一、地二、天三、地四、天五、地六、天七、地八、天九、地十；天数五，地数五，五位相得而各有合。天数二十有五，地数三十，凡天地之数五十有五。”周易所说的这种取自然数中前5个奇数和前5个偶数相加和为55的情形，大概是古人觉得55这个数字有着非同一般的寓意。实际上，其他数列的运算中也常能见到55，如连续取5个相连的三角形数3、6、10、15、21的和是55，1、2、3、4、5的平方数之和也是55，斐波那契数列的第10项也是55。这些运算或许可以给算法教学带来些许趣味。

有学者认为要从计算工具使用的角度，来揣摩古人对于数的理解。[1]例如，简单地摆放2根算筹，自然而然就会在中间形成1个空位，这就是天一地二说法的由来。笔者由此想到，古人在使用算筹来计数时，表示每一位数字最多用5根算筹，为了表示6，就需要用一根方向不同的算筹代表5根算筹。图1所示就是一种纵式的算筹摆放样式，当数字超过5时，就用一根横放的算筹代表5。如果用10根算筹摆放成55，那么无论是十位数加1，还是个位数加1，都会使算筹的摆放形态发生重大的变化，这或许是55的另一个特殊之处吧。

图1 纵式算筹摆放样式

一般人大概不太会注意到，算筹加1运算有其奇特之处，在5向6变化过程中，对于纵向摆放的算筹，事实上并非满5发生变化，而是满6才发生变化，当纵向算筹满6时，需要将纵向的5根算筹换为1根横向算筹，同时留下1根纵向的算筹。而在9向10变化的过程中，对于所有算筹，也可以看成是满6发生变化，当在4根纵向算筹和1根横向算筹的基础上再加上1根算筹，就需要将所有纵向算筹和1根横向算筹全部清空并进位。横式算筹摆放方法如图2所示，如果将数字5用摆成横向的1根算筹来表示，就会和横式算筹摆放样式中数字1所使用的图样发生混淆。可见，算筹样式的成型，与编码的唯一性有关。

图2 横式算筹摆放样式

用算筹做加法，一般采用两种方法，其一是逐个增加算筹并实施算筹满6时的变化，其二是采用算筹歌诀做快速的变化。笔者未查阅到完整的算筹歌诀，但因为珠算实际就是从算筹演化而来，因此，珠算口诀直接就可以用于算筹，如“六上一去五进一”的口诀，对算筹的使用，就是指当已有数字存在上筹（纵式中的横杠或横式中的竖杠，借用珠算中上珠的称谓，暂且称作上筹）的时候，为了加上数字6，就需要移除上筹，再添加上1根算筹，同时进位添加1根算筹。很显然，这就是一种算法。这种算法很适合于人来使用，而且，根据算筹的计算原理发明出算盘之后，采用这样的算法会使得计算速度有极大的提高。但对于某个完全自动化运转的装置来说，采用这样的算法却是徒增麻烦。可见，哪一种算法更适用，与可用和被使用计算之物有关。

● 逻辑与映射

将算筹的变化和用计算机模拟算筹的变化这两件事联系在一起，就能发现，实现“如何变”的方法是极其丰富的。算法之变和人们可借助的计算之物有着密切的关联，这里的“物”指的既可能是物质实体，也可能是一种虚拟物，

例如，可以利用if语句编写简单的程序，将数字转化为算筹的摆放样式，为简便起见，这里暂且只考虑输入一位数的情况。方法一如图3所示，程序中用“|”代表1根算筹，用“____”代表1根上筹，程序中“ ”的作用是回车换行，目的是用上下两行符号拼接成一个类似算筹摆放的图样。为后续行文方便将此方法称为方法一，这种方法体现出一种映射关系，即对于输入的数字符号，一定有其对应的输出的算筹摆放样式。

图3 一种将数字转化为算筹摆放样式的程序代码

如果将变量x视作某物，将分支结构的语句也视作某物，若在头脑中将语句与变量之间的协同变化比拟成某实体装置的变化，则想象出来的场景很可能是会有很大差异的。例如，可以想象变量x是一个带有某种属性的不动的物体，而分支结构的机械装置则会获取其属性状态并给出相对应的输出；或者，变量x是一个运动着的物体，由某个类似流水线的装置将其载入到某个判别装置中……这样的想象能让人发现头脑对于虚拟之物的利用是超越物质实体的，在想象过程中，判别装置的行为好像一个黑箱，其内部究竟是如何工作的，则是更难想象出来的事情。

● 数据存储与查表

另一种实现方法是将算筹所有的摆放样式都存放于列表中，然后将输入的数字作为索引号，从列表中调取出摆放样式。这里将其称为方法二（如图4）。

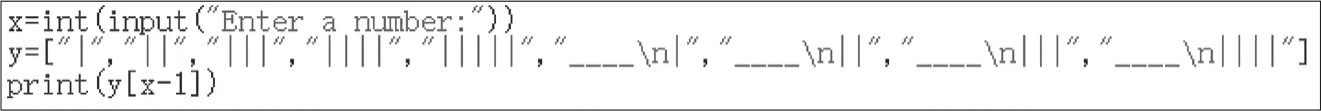
图4 从列表调取算筹摆放样式

这些存储在列表中的图样很容易存储到其他存储器中，这样就容易实现数据的共享，在一定程度上体现出存储数据的意义。类似的方法有时会在计算机的算力有限时使用，如一些单片机在进行比较复杂的函数计算时，为了加快计算时间，就会采用数学计算和查表结合的方法来得到函数计算结果。[2]

可以想象某个机械装置根据用户输入的特定序号，到存储空间中选取出相应的图样。想象中的工作场景显然和方法一是有很大区别的。

● 模式与自动化

不妨将先前的程序代码与图5所示的方法三的程序代码做一个比较。由于算筹图样在增加的过程中有一定的规律，所以，可以通过数字的比较来判断是否满6，由此确定是否要添加1根上筹，而其他纵向摆放的算筹都可以自动化批量生成。虽然说这三种方法都自动化地实现了数字转换为算筹摆放样式的工作，但方法三这个自动化装置的内部构造本身存在着某种自动化，方法一和方法二的自动化是针对使用者来说的，而方法三的自动化是针对装置的制造者来说的，如果方法三的自动化装置是一个实体装置，其设计和制造的难度显然是要高于前者的，相对前者，它还要实现构造上的自动化，具有一定程度的元自动化的特征。

图5 使用分支结构实现数字转化为算筹摆放样式的程序代码

用数字乘上字符串是Python中特有的方法，如果使用其他程序语言，就需要采用循环结构的语句来批量按数字生成纵向的算筹图样。如果将Python语言视作虚拟物，那么这种物具有其他程序语言所不具备的特征，王荣良老师提出，算法的学习需要体现计算模型的构造过程，学生需要用具体编程语言来表达算法，这不是单纯用流程图能替代的。[3]笔者从计算之物能力切入进行思考，也能得到同样的结论。

这里有一个有趣的问题，如果是由人来摆放算筹，那么此人头脑中的过程，是更接近于方法一、方法二还是方法三呢？设想某人初学算筹，在开始阶段，大概是必须要记得满6就将5根算筹换成1根上筹，这就需要简单的逻辑判别，比较接近于方法三的程序代码中分支结构判断的行为，如果此人使用算筹已经非常熟练，那么估计头脑中就会建立起牢固的数字和算筹摆放样式的对应关系，则更接近方法一和方法二代码的行为方式。

甚至于可以单纯使用数学模型来替代分支结构的逻辑判断，程序代码如图6所示。

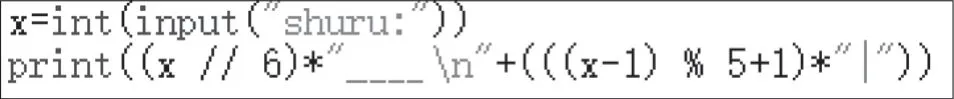
图6 采用数学模型实现数字转化为算筹摆放样式的程序代码

这种方法距离人的头脑的行为方式就非常远了，如果不是有意要利用数学，人们的头脑几乎很少用这样的方式来解决日常性的问题。假设有某个实施判别动作的机械装置，如果这个机械装置内部是借助数学运算来进行决策的，那么人的头脑是很难想象出这种数学运算是如何与装置内部物质实体的变化相关联的。这就说明，计算机程序中的数学公式已然成为一种可用于计算的虚拟物，它和数学课堂里的数学公式的意义是有所不同的。同时，计算机之所以具有当前的计算能力，和底层的数学模型是密切相关的，人们之所以很难发现这些底层数学模型是如何工作的，是因为人们所接触的系统，是由底层模型一层层虚拟出来的某种计算模型。

● 计算模型的能力和易构性

某些计算模型对实现算筹摆放样式生成相当有用。例如，可以借助字符串重写模型来实现将数字转换为算筹摆放样式的功能，程序代码如图7所示。这种方法相当于是将数字所对应的算筹全部摆放到桌面上，然后将其中6根算筹替换成1根算筹和1根代表着5根算筹的上筹。这种方法显然很不符合人的思维习惯，但对于一个具有替换功能的装置来说——如果的确有的话，实现起来却相当简单。但这样具有替换功能的装置却是不太容易制造出来的，虽然Python中有replace函数可用，但本质上，是因为首先有了Python这种图灵完备的计算装置，然后才在此基础上编写出replace函数。所以说，虽然字符串重写模型很容易实现算筹样式变化，但这个模型本身却是不容易构造出来的。而其他多种计算模型，如元胞自动机、Tag系统等，在实现算筹摆放样式的模拟上都比较困难，而如图灵机、时序数字电路这样的计算模型在实现时就相对容易一些。有意思的是，人们可以用一种计算模型来模拟另一种计算模型，如用元胞自动机来模拟图灵机，然后用图灵机来模拟算筹摆放样式。

图7 用字符串替换的方法实现数字转化为算筹摆放样式的程序代码

Python中的replace函数将替换功能内部的复杂性掩盖了起来，替换的实现并非自然而然的。设想一下，如果现实世界中存在某种神奇的自然之物，可以实现符号编码的匹配和替换，那么人们或许就会直接利用这种东西来实施自动化的计算，并且演化出各种基于匹配和替换的算法了。对计算的实现而言，人思维中的自然的变化和现实世界中自然的变化是很不相同的，人需要利用自然界中的自然之物的变化，去构造出一种能够模仿人的思维变化的东西。庄子说，“圣人者，原天地之美而达万物之理，是故至人无为，大圣不作，观于天地之谓也”，前半句很有道理，后半句却值得商榷，假设人脑所构造的计算模型无法由实际的计算装置开展直观地运算，那么人在通达万物之理的路途上就会遇到很大的阻碍。