航空摄影测量双像解析定位精度分析
2023-01-29冯建龙
冯建龙
(吉林省第二地质调查所,吉林 吉林 132013)
0.引言
在航空摄影测量中,通过一个双像立体像对,利用其重叠范围区域的同名像点,我们可以恢复出在参考坐标系下,左像片、右像片在拍摄时的方位以及同名射线的方向,同名射线对对相交,由同名射线的交点可以确定出地面点的空间坐标。根据立体像对上获得的已知数据确定地面点空间坐标的过程中,会有很多的误差产生,从而使计算得到的地面点空间坐标与其真实的空间坐标产生偏差,影响地面点空间坐标的精度确定[2]。
本文中,我们主要采用解析摄影测量的后方-前方交会法和相对定向—绝对定向法两种定位方法。同时,在前方交会过程中采用三种投影系数计算方法来确定地面点坐标并分别评定其精度,然后将精度评定结果与相对定向—绝对定向法的精度对比,从而来完成双像摄影测量定位精度分析工作。
1.双像解析空间前方交会
假设在空中有两个摄影点S1、S2,对地面进行摄影获得一个立体像对如图1所示,D-XYZ是地面摄影测量坐标系,S1-U1V1W1为左像片的像空间辅助坐标系,S2-U2V2W2为右像片的像空间辅助坐标系,两个像空间辅助坐标的三个坐标轴分别与D-XYZ的三个坐标轴平行。设地面点A在地面摄影测量坐标系D-XYZ下的坐标为(X,Y,Z),地面点A在左像片的像空间辅助坐标系下的坐标为(U1,V11,W1),在右像片的像空间辅助坐标系下的坐标为(U2,V21,W2)。地面点A在该立体像对左、右像片上的构像为a1、a2,像点a1、a2在各自像片的像平面坐标系下的坐标分别为(x1,y1,-f)、(x2,y2,-f),在像辅助坐标系下的坐标分别为(u1,v1,w1)、(u2,v2,w2),根据空间坐标系转换关系可得像空间坐标和像空间辅助坐标之间的关系式,如式(1)所示:
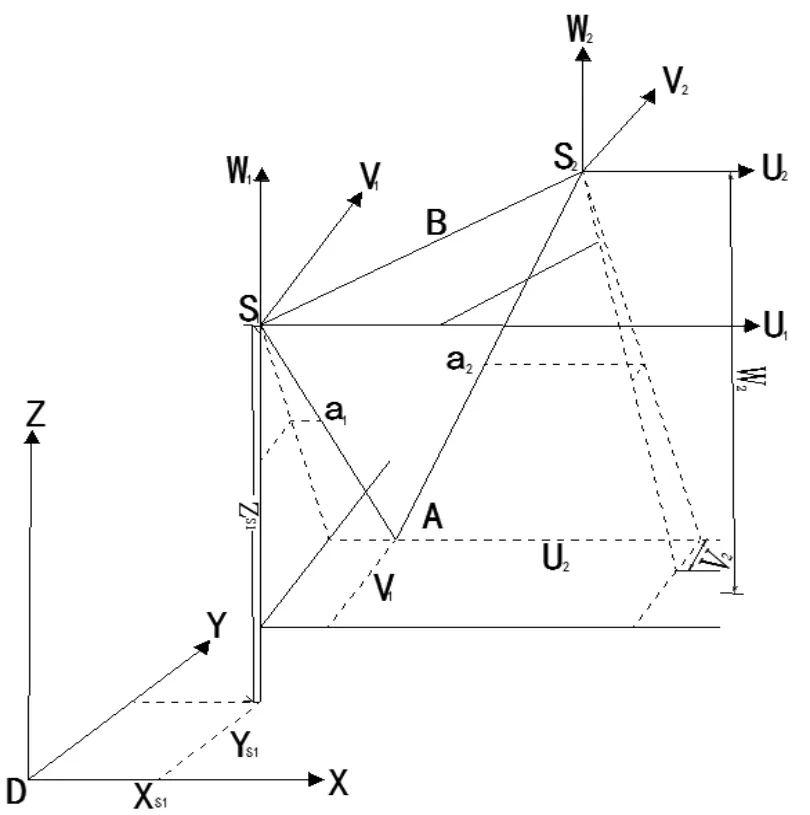
图1 立体像对空间前方交会
式(1)中,R1、R2分别为左右像片的旋转矩阵。
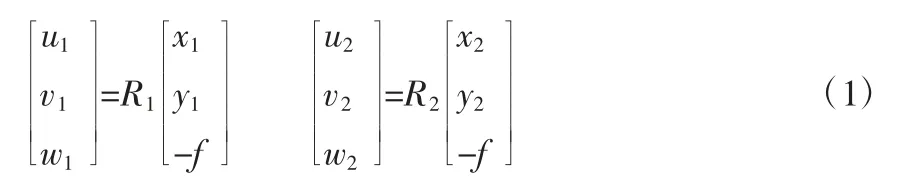
双像解析摄影测量,是通过解析计算的方法来分析处理一个空间立体像对的影像信息,从而来获得地面点的空间位置[4]。利用双像解析的空间后方-前方交会法来解算地面点的空间位置,其具体步骤如下。
1.1.1 野外像片的控制测量
一个空间立体像对如图2所示,在左、右像片重叠区域的四个角上,找到四个明显的地物点来作为空间立体像对的控制点。同时,在野外判读出这四个明显地物点的实际地面位置,并做出相应的地面标志,在像片上准确地刺出控制点位置,并在像片的背面加注和说明。然后,在野外采用普通的测量方法分别计算得到四个控制点在地面测量坐标,并通过坐标转换关系式转化为地面摄影测量坐标(X,Y,Z)。
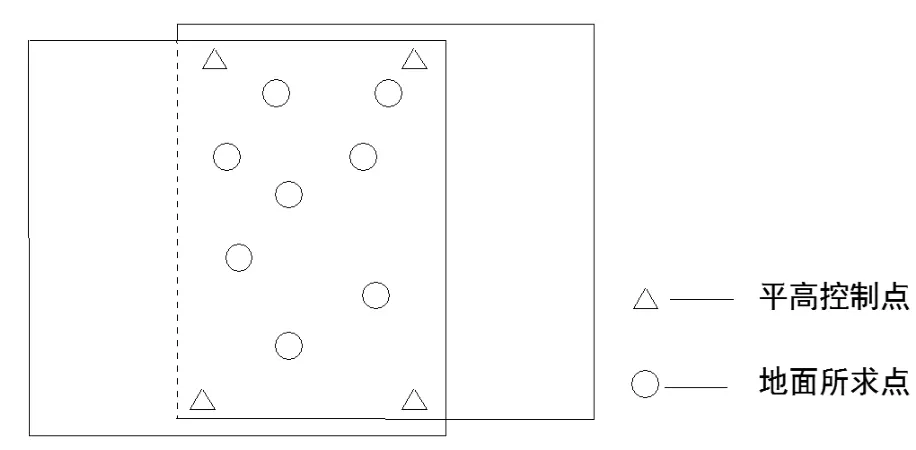
图2 立体像对的控制点和待求点
1.1.2 量测像点坐标
利用立体坐标量测仪将立体像对进行定向归心后,测出立体像对重叠区域的四个控制点的像点坐标以及所有待求点的像点坐标。
1.1.3 单像空间后方交会计算像对左、右像片的外方位元素
利用控制点在像方坐标系下的像点坐标和对应的在物方坐标系下的坐标,通过单像空间后方交会的计算方法,可以分别计算左、右像片各自对应的六个外方位角元素[5]Xs、Ys、Zs、φ、w、k。
1.1.4 空间前方交会解算待定点的地面坐标
根据立体像对左、右像片各自的外方位角元素计算左、右像片的方向余弦,组成各自的像空间坐标系和像空间辅助坐标系之间转换的旋转矩阵R1、R2。然后根据左、右像片待求点的像空间坐标,通过坐标转换关系式逐点解算各个待求点的像空间辅助坐标,并根据外方位元素计算立体像对的摄影基线B的三个坐标分量Bu、Bv、Bw,以及左、右像片的投影系数N1、N2。利用左、右像片计算得到的投影系数N1、N2,通过前方交会基本关系式,计算待求点地面点分别在左、右像片的像空间辅助坐标系下的坐标(U1,V11,W)1和(U2,V21,W2)。最后,根据立体像对计算地面点坐标的空间前方交会基本关系式,计算出待定点对应的地面坐标。
2.立体模型解析法绝对定向
立体像对相对定向的过程仅仅是恢复了在摄影时左、右像片的相对位置,因此建立起来的相对定向模型是一个以相对定向过程中选定的像空间辅助坐标系作为基准的立体模型,而且整个模型的比例尺也是未知的。要确定模型点在地面摄影测量坐标系下的地面坐标,还需要把立体模型中模型点在像空间辅助坐标系下的坐标转换为地面摄影测量坐标系下的坐标(X,Y,Z)。这一工作的实现,需要借助地面摄影测量坐标为已知值的地面控制点,叫作立体模型的绝对定向。
绝对定向基本关系式,如式(2)所示:
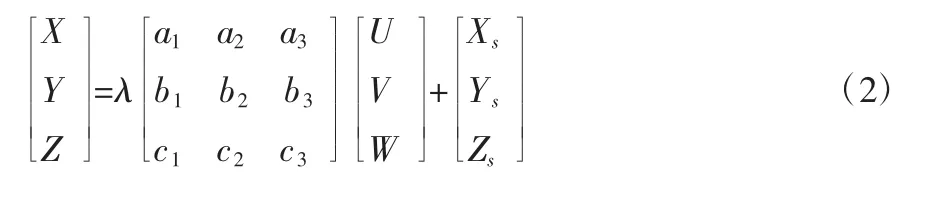
式(2)中,(X,Y,Z)为控制点的地面摄影测量坐标;(U,V,W)为模型点的像空间辅助坐标;λ为模型比例尺缩放系数;Xs、Ys、Zs为坐标原点的平移量。通过式(2),我们可以实现模型点的像空间辅助坐标和地面摄影测量坐标的转换,转换前后图形的几何形状是相似的,所以这个变换过程又称为空间相似变换。绝对定向基本关系式中的旋转矩阵中的各个元素,是通过两个坐标转换轴系的三个角元素φ、w、k计算得到。所以绝对定向基本关系式中包含七个绝对定向元素,即模型比例尺缩放系数λ;坐标轴三个角元素φ、w、k;坐标原点在三个方向上的坐标值Xs、Ys、Zs。解析法绝对定向的过程,就是利用已知地面摄影测量坐标的控制点,通过绝对定向关系式,解求上述中的七个绝对定向元素。
双像解析相对定向—绝对定向法解算模型点的地面摄影测量坐标的过程如下:
(1)通过连续像对相对定向元素的误差方程式或者单独相对的相对定向元素的误差方程式,解算相对定向模型中的五个相对定向元素;
(2)根据相对定向元素可以求得左、右像片的旋转矩阵R1、R2,通过前方交会可以求得模型点在相对定向模型的像空间辅助坐标系下的坐标;
(3)利用已知地面摄影测量坐标的控制点,将其重心化,按照求解绝对定向元素的误差方程式,解算出七个绝对定向元素;
(4)按照绝对定向基本关系式,将所有的待定点在相对定向模型中的模型点坐标重心化后,代入绝对定向基本关系式中,求解得到待定点经过重心化后的地面摄影测量坐标,然后根据地面摄影测量坐标系的重心坐标,解算得到待定点真正的地面摄影测量坐标。
3.航空摄影测量双像解析定位精度分析实例
3.1 原始数据
(1)左像片:01-157.tif;右像片:01-156.tif,如图3所示。

图3 已知数据
(2)地面GCP(控制点)标识文件:01-156_50mic.jpg;左、右像片的八个框标点的框标坐标、像主点框标坐标及像主距文件:rc30.cmr;六个同名像点的地面摄影测量坐标文件:hammer.ctl。
3.2 内定向
目前已有的数据中,我们有像片上八个框标点的框标坐标,再对像片上对应的框标点进行量测得到其像素坐标,便可通过最小二乘平差的方法求得仿射变换关系式中的各项系数。最小二乘平差求解仿射变换六个系数的实现过程,本文以MATLAB编程实现解算像素点在像平面坐标系中的坐标值如表1所示。
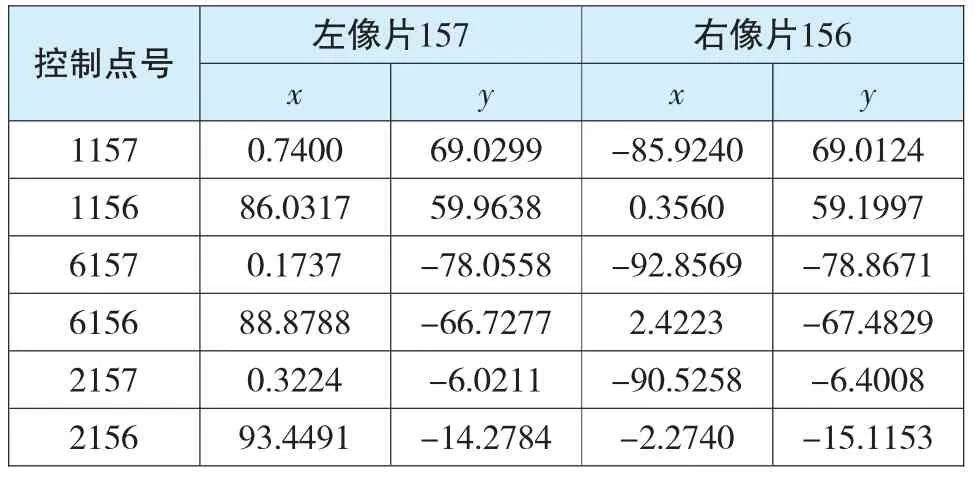
表1 像主点的像平面坐标 单位:mm
打开地面GCP(控制点)标识文件01-156_50mic.jpg,在图片中找到相应控制点的大致位置,再用电脑自带的画图软件打开左像片01-157.tif,将像片放大找到该控制点的位置,记录下控制点对应的像素坐标。以控制点1157为例如图4所示,在左像片上寻找控制点1157的像素坐标。用同样的方法可以找出左像片上所有控制点的像素坐标。右像片上各个控制点的像素坐标量测的方法和左像片相同。将各个控制点的像素坐标代入仿射变换公式中,便可求得该控制点的框标坐标。左像片和右像片控制点的框标坐标求解方法相同。像平面坐标系的原点为像主点,像主点坐标为:x=-0.004 mm,y=-0.008 mm。将控制点的框标坐标减去像主点坐标,即为控制点的像平面坐标系下的像平面坐标如表2所示。
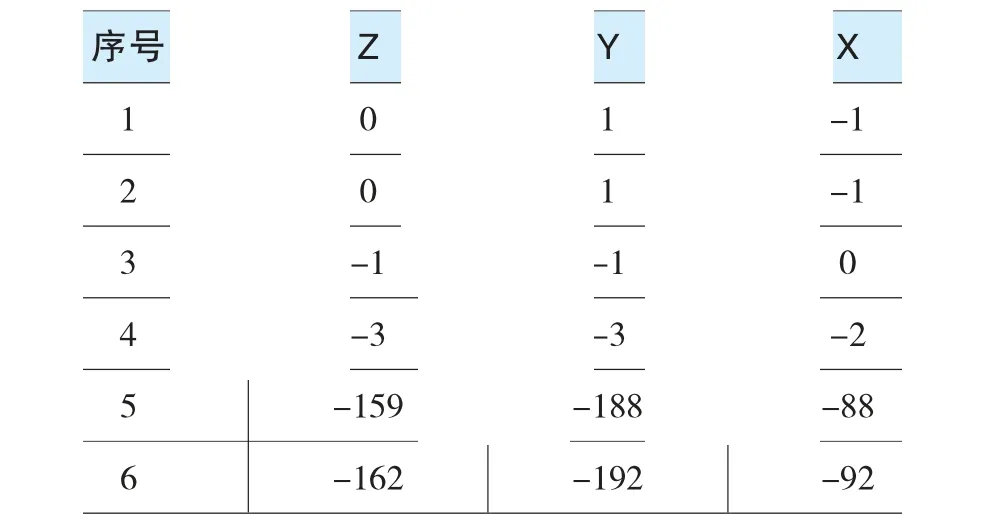
表2 模型滑坡变形值 单位:mm
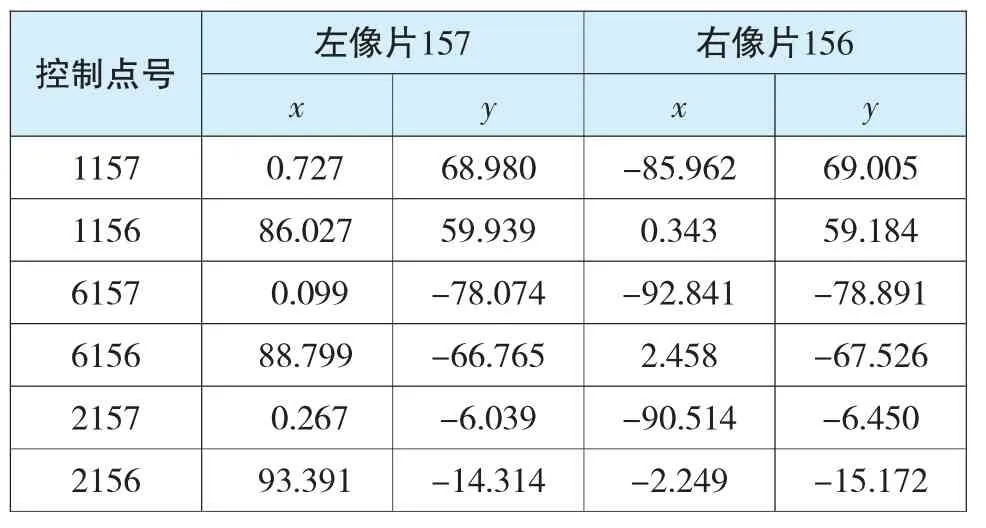
表2 控制点在像片上的像平面坐标 单位:mm

图4 量测控制点的像素坐标
3.3 后方交会及前方交会精度统计
在计算外方位元素时,采用迭代求解与最小二乘平差的方法,使得外方位元素逐渐收敛于理论值,计算左右像片的外方位元素如表3所示。

表3 左、右像片的外方位元素 单位:m
3.3.1 按照三种不同投影方法计算地面点坐标
投影系数公式如式(3)、式(4)、式(5)所示:
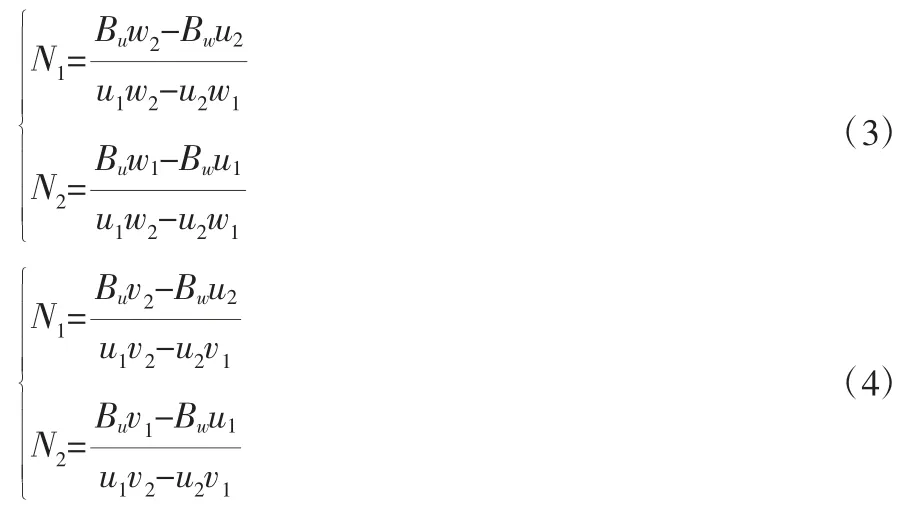

式(3)中,N1、N2为左、右像片投影系数;Bu、Bv、Bw为摄影基线三个方向上的分量;u、v、w为左、右像片在像空间辅助坐标系下的坐标。按照投影系数三个公式计算地面点坐标如表4所示。

表4 三种投影精度对比表 单位:m
根据三种投影系数计算控制点地面摄影测量坐标的精度分析结果,将三种投影系数计算方法计算得到的控制点地面摄影测量坐标的平面中误差mxy、Z方向中误差mz以及总的中误差m,分别比较:
(1)前两二种投影系数计算方法计算得到的控制点地面摄影测量坐标的精度较高,且第一种投影系数计算方法的精度优于第二种投影系数计算方法;
(2)第三种投影系数计算方法计算得到的控制点的地面摄影测量坐标的精度,在三种计算方法中精度最低,且其精度远低于前两种;
(3)绝对定向与相对定向精度评定
本文中,假设模型点2157、2156两点的地面摄影测量坐标未知,通过绝对定向基本关系式解算出它们的地面摄影测量坐标,然后与它们真实的地面摄影测量坐标比较,从而来评定精度。评定计算式如式(6)、式(7)、式(8)所示:
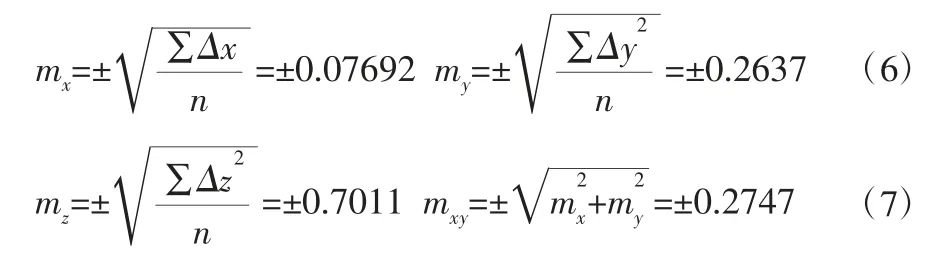

3.3.2 两者精度分析与结论
根据后方交会—前方交会三种投影系数方法以及相对定向-绝对定向方法计算控制点地面摄影测量坐标的精度结果,将计算得到的控制点地面摄影测量坐标的平面中误差mxy、Z方向中误差mz以及总的中误差m,分别比较:
(1)运用后方交会—前方交会方法进行双像解析的定位精度与空间后方交会精度及空间前方交会中左、右像片像点投影系数的计算公式有关。通过实验验证:第一种和第二种投影系数计算方法定位精度较高,第三种投影系数计算方法定位精度很低。
(2)运用相对定向—绝对定向方法进行双像解析的定位精度和相对定向及绝对定向的精度有关。通过实验可知:相对定向-绝对定向方法的定位精度较高。
(3)由实验结果可知:后方交会—前方交会定位方法中第一种和第二种投影系数计算方法的定位精度与相对定向—绝对定向方法定位精度相当,都比较高,而第三种投影系数计算方法的定位精度远低于前二者。
4.结束语
本论文通过两种确定地面点坐标的方法,即空间后方交会—前方交会和相对定向—绝对定向两种方法,来确定立体像对重叠区域的同名像点对应地面点的空间坐标。通过实例验证了每一种定位方法的优缺点与适用条件,为航测双像解析定位提供参考意见。
