一种基于地轴投影的二维重力匹配方法

毛 宁，李 安，许江宁，覃方君，李京书

（1.海军工程大学电气工程学院，武汉 430033；2.海军工程大学作战运筹与规划系，武汉 430033）

当前，适用于水下航行器的导航定位手段主要有惯性导航、水声定位导航、惯性/重力匹配组合导航以及惯性/地磁匹配导航等[1]，其中惯性/重力匹配组合导航技术利用地球重力场的空间分布，通过设计稳定的匹配算法，可以有效抑制惯性导航系统随时间累积的误差，满足水下航行器长航时、高隐蔽性的航行要求。因此，重力辅助惯性导航技术是目前水下载体自主导航的重要研究方向，也是水下定位、导航与授时（Positioning,Navigation and Timing,PNT）体系建设的重要组成部分[2]。

惯性/重力匹配组合导航系统主要包括惯性导航系统、重力仪、重力基准图（即重力异常背景场）以及匹配算法四部分，其中匹配算法是重力匹配导航中的一项关键技术，用于实现重力匹配以修正惯性导航系统随时间累积的误差。

目前重力匹配导航算法的研究主要有两类：一类是基于滤波技术的单点迭代匹配算法，如SITAN[3]、粒子滤波算法[4]等；另一类是基于相关极值的序列迭代匹配算法，如TERCOM、ICCP 等。另外还有多种算法联合匹配导航技术[5]；基于智能优化算法[6,7]、机器学习算法[8]等的重力匹配导航技术。

国内外学者对于重力匹配导航算法的研究，大多从20 世纪90 年代开始。Han 等提出了一种滤波递归和轨迹相似变换相结合的匹配算法，首先利用点群滤波进行初匹配，然后再通过相似性变换进行二次匹配，结果表明经度和纬度误差的标准差均优于1′[9]。Liu 等通过在Walsh-Hadamard 核函数中引入Hadamard 变换过程，提出了一种基于多尺度搜索和Hadamard 变换差分的重力匹配导航算法，仿真结果表明该算法对测量次数、测量精度和匹配面积的要求较低，40 个测量样本点的匹配精度优于1′，且具有较高的匹配成功率和匹配效率[10]。蔡体菁等将相关极值匹配过程分为了粗匹配和精确搜索两部分，提出了一种两步式相关极值重力匹配算法，通过将重力背景图细化为0.06′×0.06′，仿真结果显示定位误差优于0.5′[11]。欧阳明达等通过在SITAN 算法中引入抗差估计方法，改善了算法在粗差探测上的不足，仿真实验达到了优于1海里的导航精度[12]。李晓平等利用15 条船载实测数据分析了重力仪测量误差和惯导误差对匹配精度的影响，并验证了所提匹配影响因素的平衡关系和匹配误差模型的有效性[13]。

有效匹配是指在一次序列匹配中，所有匹配点的位置误差均在设定的安全范围ΔPm内，则有效匹配率是指在n次序列匹配中，有效匹配所占的比例，是序列匹配方法中一个重要的指标，误匹配的概念则与有效匹配相反[14]。针对一维匹配中容易出现误匹配从而造成可靠性不高的问题，文献[14]根据傅里叶变换具有的平移不变性，利用归一化功率谱作为相关性测度，建立载体航迹与重力异常背景图之间的联系，提出了一种“载体特定航迹+重力异常背景场”的二维重力匹配方法；文献[15]将图像匹配的思路引入重力匹配导航中，通过将重力异常数据转换为0～255 之间的灰度值，利用两幅重力二维图像中同一种纹理特征之间的关联度实现二维匹配。但上述二维匹配方法均需要引入额外的限制条件，降低了适用性。

由于重力仪测量误差的存在，重力匹配算法在搜索等值点时搜索阈值Δg的设定是十分重要的，Δg设置过大会增加算法误匹配的概率，设置过小则可能无法找到有效的等值点。另外，大多数重力匹配算法是利用重力异常值的大小进行匹配，即重力背景场和匹配过程中均使用重力大小的一维数据，且研究重点主要集中在匹配算法的优化和改进上。因此，当前大多数重力匹配算法在重力异常变化明显的区域有较好的匹配结果，但在重力信息变化较为平缓的区域，其匹配误差较大，甚至出现误匹配，使得重力匹配技术的应用受到了较大限制[13]。

因此，本文提出一种基于地轴投影的二维重力匹配方法，该方法首先将重力异常信息沿地球自转轴进行分解，建立二维重力异常数据库，然后根据惯导提供的纬度信息将重力仪测得的重力异常信息进行分解，并利用分解后的重力信息进行二维匹配导航，最后根据迭代最近等值线（Iterative Closest Contour Point,ICCP）和地形轮廓匹配（Terrain Contour Matching,TERCOM）算法，设计了二维重力匹配的V-ICCP 和V-TERCOM 算法，并对所提方法有效性进行了验证。

1 基于地轴投影的重力二维分解

基于地轴投影就是将重力标量数据沿着地球自转轴方向进行二维分解，如图1 所示，图中g为重力异常信息，通过将g二维分解，一部分分量是重力向地球自转轴方向投影，记为gω，剩余分量根据重力矢量三角形分解确定，记grest。接下来分别阐述当前重力矢量测量的难点以及基于地球自转轴方向二维分解重力信息的优势。

图1 二维重力分解示意图Fig.1 Schematic diagram of 2D gravity decomposition

1.1 重力矢量测量的难点

矢量重力仪直接测量载体系下三轴重力分量，当载体处于时变的复杂运动时，载体系基准未知，不利于重力矢量监测与比较，通常将加速度计所测载体系三轴重力分量通过姿态旋转矩阵，表征在已知的参考基准内。当前，无论是平台式重力仪还是捷联式重力仪均将当地地理坐标系作为重力矢量的参考基准，确定基准的过程即是姿态求解过程[16]。

文献[17]指出1"的姿态误差即可引起6～8 mGal的水平扰动，如式(1)所示，取g=10 m/s2，按照姿态误差为1"得到重力水平分量的测量误差为5 mGal。即重力信息在水平方向分解的信息量太少，极易被淹没在由姿态误差引起的测量噪声中。

因此将当地地理坐标系作为重力矢量测量的姿态基准时，绝大多数重力信息被分解到垂向，仅有极少量的重力信息分解到水平向，且这极少量的重力水平分量很容易被淹没在测量噪声或者姿态误差引起的测量噪声中，故这种“水平”“垂向”的分解方式使得重力矢量信息的矢量可观测性很差。

1.2 基于地轴投影的优势

根据上述分析，本文提出了一种基于地球自转轴指向的重力二维分解方法，将重力向地球自转轴进行投影，除了赤道和极区附近，其他区域均能够保证重力在地球自转轴方向和剩余分量均有足够的重力信息。与文献[14][15]中二维重力匹配方法不同的是，本文所提基于地轴投影的方法充分考虑了重力异常数据的特征，可以在不增加额外限制条件的情况下实现二维重力匹配，提高有效匹配率。

利用重力信息分解后在水平方向的信噪比大小，分析基于地球自转轴重力二维分解方法的优势。取g=10 m/s2，在纬度为45 °的位置附近对重力进行分解，假定垂线偏差为3"，姿态误差是幅值为1"的随机噪声。式(2)为本文所提方法在水平方向的信噪比，式(3)为传统以当地地理系为基准，在水平方向的信噪比。可以看到，本文所提方法不仅增加了该水平方向的信号强度，同时降低了该方向的噪声强度，信噪比由约12 dB 提高到约106 dB。

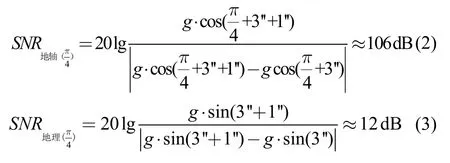
本文所提方法中，地球自转轴指向可通过惯性元件自主确定，相比地理坐标系，从机理上惯性元件能够更准确地给出该基准与载体系的投影关系。另外，重力向地球自转轴方向投影时，投影角度可看作是纬度的余弦，即得到的重力二维分解数据具有纬度标签，尽管该纬度是近似的纬度，但可看作带有纬度标签的重力场窄带，特别有利于水下重力匹配导航的应用需求，相比重力匹配导航广域重力场图而言，这一优势缩小了匹配空间，提高了重力场的实用性。

选择某海域进行等值点搜索仿真实验，重力异常基准图选择美国斯克里普斯海洋研究所Sandwell 团队发布的卫星测高反演重力异常数据[18]，分辨率为1′ × 1′，精度3 mGal。在不考虑重力仪测量误差的情况下，选择点A（122.4250°E,35.2075°N,4 mGal）作为基准点进行等值点搜索。如图2 所示，在传统重力异常基准图g中搜索得到了20 个等值点。如图3 所示，将重力基准图按照本文所提方法分解为gx和gy，然后搜索位置A 分解后的等值点，分别得到6 个和2 个等值点，并通过分析等值点的位置坐标，最终得到有效等值点为图中箭头指向的2 个。

图2 传统重力异常背景图g 中等值点搜索结果Fig.2 Search results of equivalence points in g

图3 重力二维分解后等值点搜索结果Fig.3 Search results of equivalence points in gx and gy

通过上述分析可以得到，本文所提方法可以有效剔除纬度与真实位置点纬度相差较大的等值点，缩小了等值点的范围，有利于提高算法的可靠性。

2 二维重力匹配算法

利用第一节所述重力分解方法，构建二维重力匹配的TERCOM 算法和ICCP 算法模型。首先分别介绍了两种算法的传统模型，阐述了这两种序列迭代匹配方法容易出现误匹配的问题，并针对此问题建立了两种算法的二维匹配模型，设计了V-ICCP 和V-TERCOM 算法。

本文提出的二维匹配算法在等值点的搜索方法上与一般的序列匹配算法保持一致，所不同的是，利用本文所提方法将重力异常沿地球自转轴进行分解后，重力二维分解数据可看作带有纬度标签的重力场窄带，分解后的二维重力信息进行等值点搜索时会受到纬度信息的约束，即需要在分解后的两个维度均满足重力分解条件。

因此，按照本文所提方法进行等值点搜索时会同时受到两个维度重力异常大小的约束，而用一维序列迭代匹配方法进行等值点搜索时只有重力异常大小的约束，故该算法在一定程度上缩小了等值点的搜索范围，同时也限制了误匹配发生的概率，提高了算法的有效匹配率。

2.1 TERCOM 算法模型

TERCOM 算法是利用惯导指示航迹，在重力背景场中寻找一条重力异常值与实测重力异常值相关程度最高的路径。记惯导指示航迹上实测重力异常值构成的点集为Gm=，在重力背景场中搜索与惯导指示航迹等长度的一系列重力异常点集Gs=（一般根据惯导指示航迹进行平移和旋转搜索），然后计算轨迹M和S之间的相关程度。一般利用互相关（COR）、平均绝对差（MAD）或均方差（MSD）来判断轨迹间的相关程度，其计算方法如下所示。

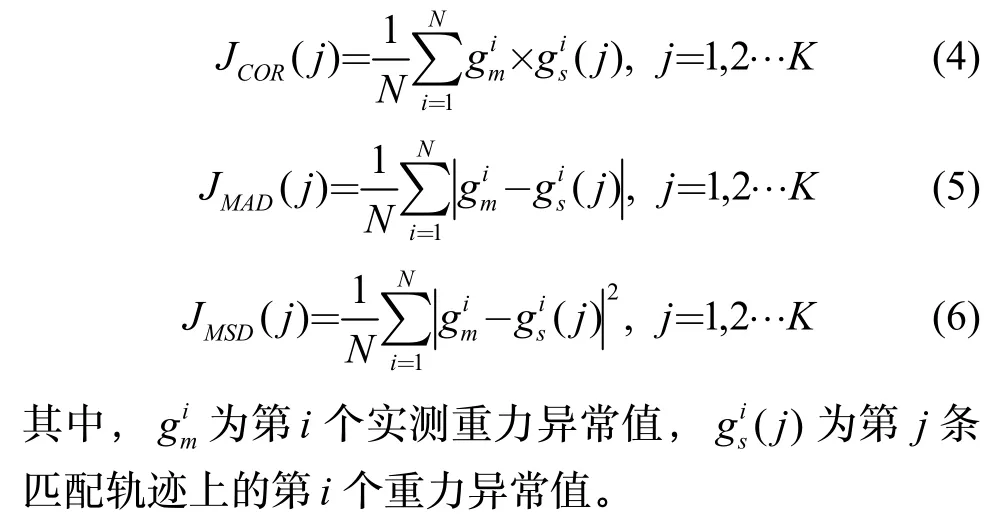
最佳匹配路径就是使性能指标JCOR最大，或者使性能指标JMAD、JMSD最小的轨迹。在TERCOM 算法实际使用过程中，均方差JMSD的精度较高，一般可作为评估匹配重力异常剖面与实测重力异常剖面相关程度的指标。

为避免因搜索计算量过大影响算法的实时性，TERCOM 算法通过分析惯导输出数据，利用瑞利分布得到惯导指示航迹点的位置误差范围（即置信区间），然后根据重力仪的测量精度设定等值点搜索阈值Δg，在置信区间内搜索所有满足的等值点。

根据上述分析可知，TERCOM 算法中搜索阈值Δgi的设置会影响匹配精度，设置过大会使其误匹配发生的概率增加，而设置过小则会影响算法找到有效匹配点。

与 TERCOM 算法不同的是，本文所提的V-TERCOM 算法利用沿地球自转轴分解的重力异常信息进行匹配，该算法在搜索等值点时，必须同时在Ex和Ey两个方向满足设定的阈值Δgx和Δgy，增加了限制条件，限制了等值点搜索的范围，V-TERCOM的算法流程如表1 所示。

表1 V-TERCOM 算法流程Tab.1 Algorithm procedure of V-TERCOM

2.2 ICCP 算法模型

ICCP 算法是一种在重力匹配技术中应用较多的算法，如图4 所示，其根据惯导指示航迹点的量测重力值，在等值线Ci上搜索距离最近的等值点，并利用这些等值线点构成估计航迹（即1 次迭代轨迹），然后计算估计航迹Y1与惯导指示航迹PINS之间的刚性变换参数（平移T和旋转R(θ)），再利用T和R(θ)对PINS进行刚性变换得到新的估计航迹，然后将作为新的惯导航迹进行反复迭代，直至满足终止条件。

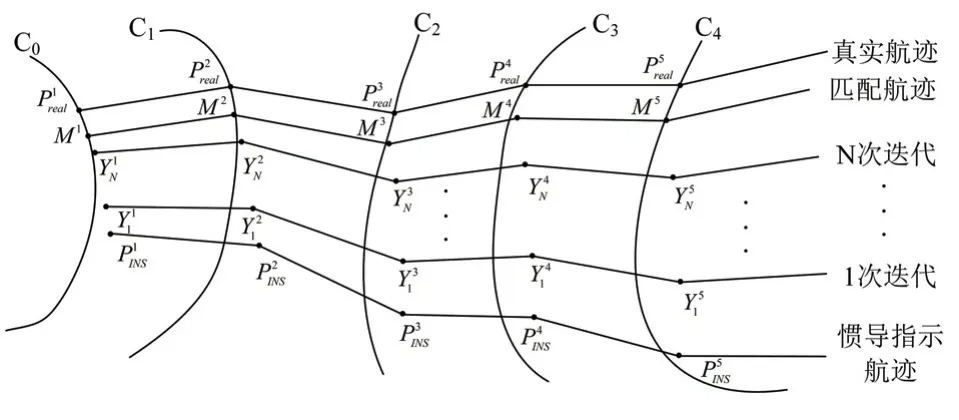
图4 ICCP 算法基本原理Fig.4 Basic principles of ICCP algorithm

常见的ICCP 算法终止条件有：①T和R(θ)的绝对值小于设定阈值Tth和R(θth)；② 相邻两次迭代之间T和R(θ)的增量小于设定阈值ΔT和Δθ；③相邻两次迭代得到的估计航迹点间的距离小于设定门限值。

根据上述分析可知，传统的ICCP 算法在搜索等值点的时候，需要考虑重力异常测量精度的影响，因此在实际应用中，并不是在等值线Ci上搜索重力异常等值点，而是在以等值线Ci为中心，以2Δg为带宽的重力异常等值带上搜索距离最近的等值点，如图5 所示。

图5 ICCP 算法等值点搜索范围Fig.5 Search area of equivalent points in ICCP algorithm

因此，对于ICCP 算法来说，搜索阈值Δg的确定是非常重要的，设置过大会增加误匹配的概率，还会造成计算量的增大，而设置过小算法则可能无法找到有效匹配点，从而无法得到匹配航迹。

针对此问题，本文提出了V-ICCP 算法，该算法将重力异常信息沿地轴进行分解，分别在水平和垂直两个维度上对重力异常等值点进行限制，如图6 所示。

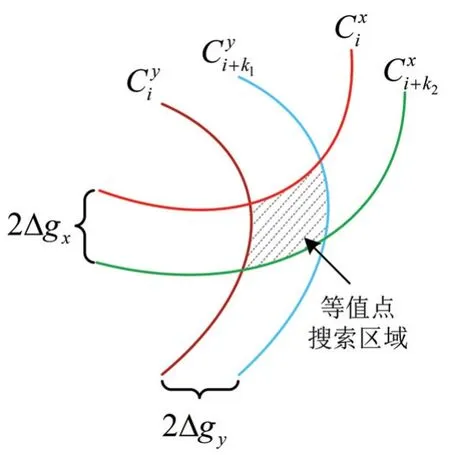
图6 V-ICCP 算法等值点搜索范围Fig.6 Search area of equivalent points in V-ICCP algorithm

与传统ICCP 算法在以2Δg为带宽的重力异常等值带上搜索等值点相比，V-ICCP 算法在搜索等值点时，需要同时满足分别以2Δgx和2Δgy为带宽的重力异常等值带，即搜索区域为这两个等值带重合的区域，在一定程度上缩小了等值点的搜索范围，同时也限制了误匹配发生的概率，提高了搜索效率，V-ICCP 的算法流程如表2 所示。

表2 V-ICCP 算法流程Tab.2 Algorithm procedure of V-ICCP

3 试验验证与分析

选择某海域进行等值点搜索仿真实验，重力异常基准图选择美国斯克里普斯海洋研究所Sandwell 团队发布的卫星测高反演重力异常数据[18]，分辨率为1′ × 1 ′，精度3 mGal，如图7 所示。

图7 重力异常背景图Fig.7 Gravity anomaly background

3.1 实验设计

如图8 所示，通过仿真得到3 条水下载体航行路线。根据图8 中3 条航迹对应的重力异常变化曲线可以看到，航迹上重力异常信息的变化程度依次为：航迹1＜航迹2＜航迹3。按照本文所提方法将重力异常背景分解为gx和gy，如图9 所示。

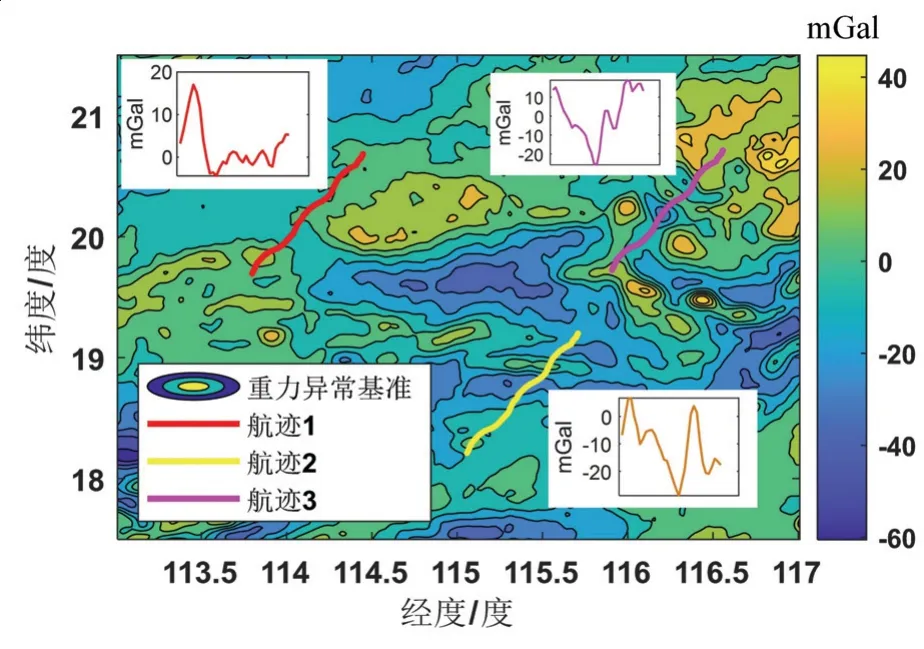
图8 仿真航迹及其重力异常Fig.8 Simulated paths and gravity anomaly

图9 重力二维分解结果Fig.9 Gravity 2D decomposition results

为了分析算法在惯性导航系统具有较大初始位置漂移情况下的有效性，本文仿真了3 条初始水平定位误差为6 海里的惯导航迹，如图10 所示，真实航迹和惯导航迹的具体参数见表3。另外，重力仪量测值由真实航迹上的重力异常加上标准差为3 mGal 的随机误差得到。

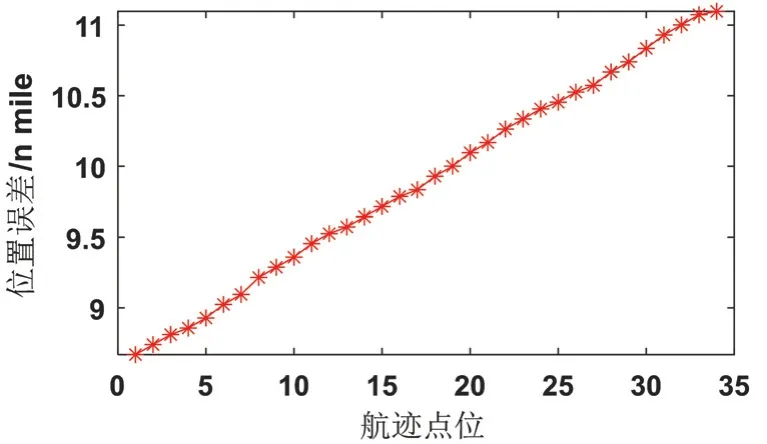
图10 惯导航迹误差Fig.10 Path error of SINS

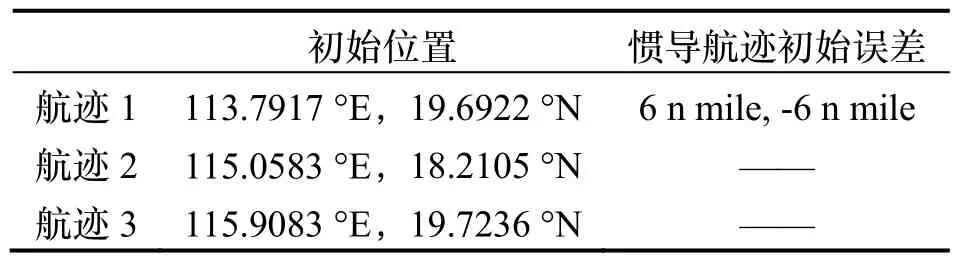
表3 仿真航迹参数Tab.3 Simulated paths and their parameters

3.2 结果分析

对不同的航迹分别利用传统ICCP、改进ICCP[19]、TERCOM 算法以及本文提出的V-ICCP、V-TERCOM算法进行匹配实验，为验证所提算法的匹配精度和可靠性，每条航迹均进行1000 次的匹配仿真实验，每次匹配除重力仪量测值外，其余条件均保持一致。

考虑到当前全球海洋重力异常基准图分辨率（1′ × 1 ′）、海洋重力仪测量精度（约1 mGal），以及水下航行器航行安全需求，本文将匹配航迹上所有点的平均误差小于1 个格网的匹配结果认为是有效匹配，存在大于1 个格网的匹配结果认为是误匹配。另外，匹配结果中匹配点误差的标准差可以用来分析匹配结果的稳定性，该值越小说明匹配结果中每个匹配点的误差水平越接近，出现某一匹配点误差很大的情况越小，即匹配航迹越稳定。

航迹1 匹配结果统计如图11 所示，可以看到在1000 次匹配实验中，传统ICCP、改进ICCP、V-ICCP、TERCOM、V-TERCOM 五种算法有效匹配个数分别为：442、439、577、248、281，即ICCP 算法的有效匹配率由44.2%提高至57.7%，TERCOM 算法的有效匹配率由24.8%提高至28.1%，提高了匹配率的同时算法保持了较好的稳定性。

图11 航迹1 匹配结果统计Fig.11 Matching results statistics of path 1

航迹2 匹配结果统计如图12 所示，可以看到在1000 次匹配实验中，传统ICCP、改进ICCP、V-ICCP、TERCOM、V-TERCOM 四种算法有效匹配个数分别为：782、801、934、282、303，即ICCP 算法的有效匹配率由78.3%提高至93.4%，TERCOM 算法的有效匹配率基本保持不变，提高了匹配率的同时算法保持了较好的稳定性。

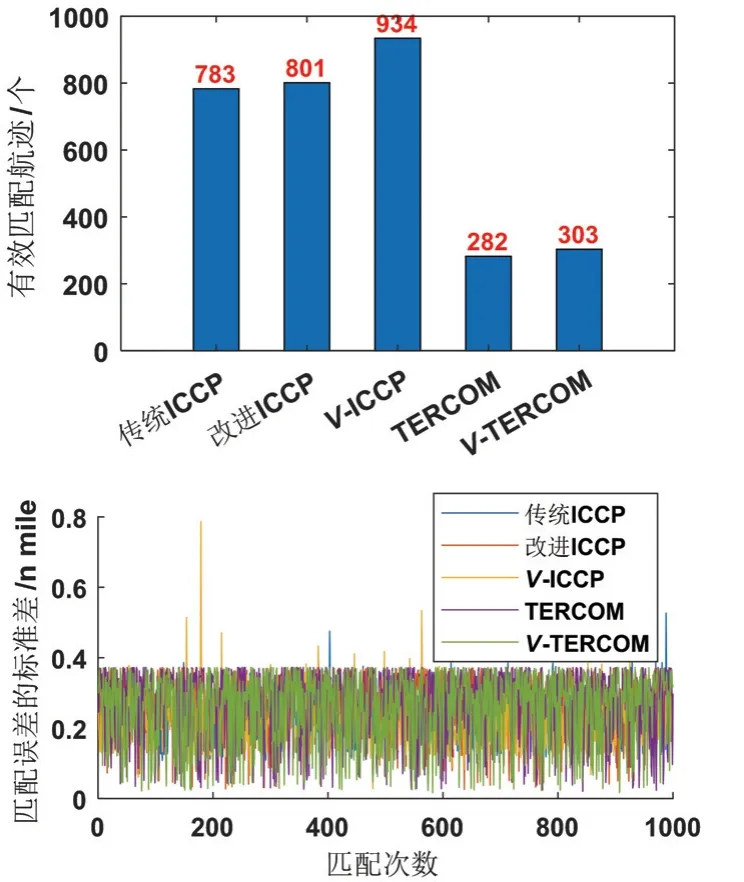
图12 航迹2 匹配结果统计Fig.12 Matching results statistics of path 2

航迹3 匹配结果统计如图13 所示，可以看到在1000 次匹配实验中，传统ICCP、改进ICCP、V-ICCP、TERCOM、V-TERCOM 四种算法有效匹配个数分别为：848、860、937、294、300，即ICCP 算法的有效匹配率由84.8%提高至93.7%，TERCOM 算法的有效匹配率基本保持不变。

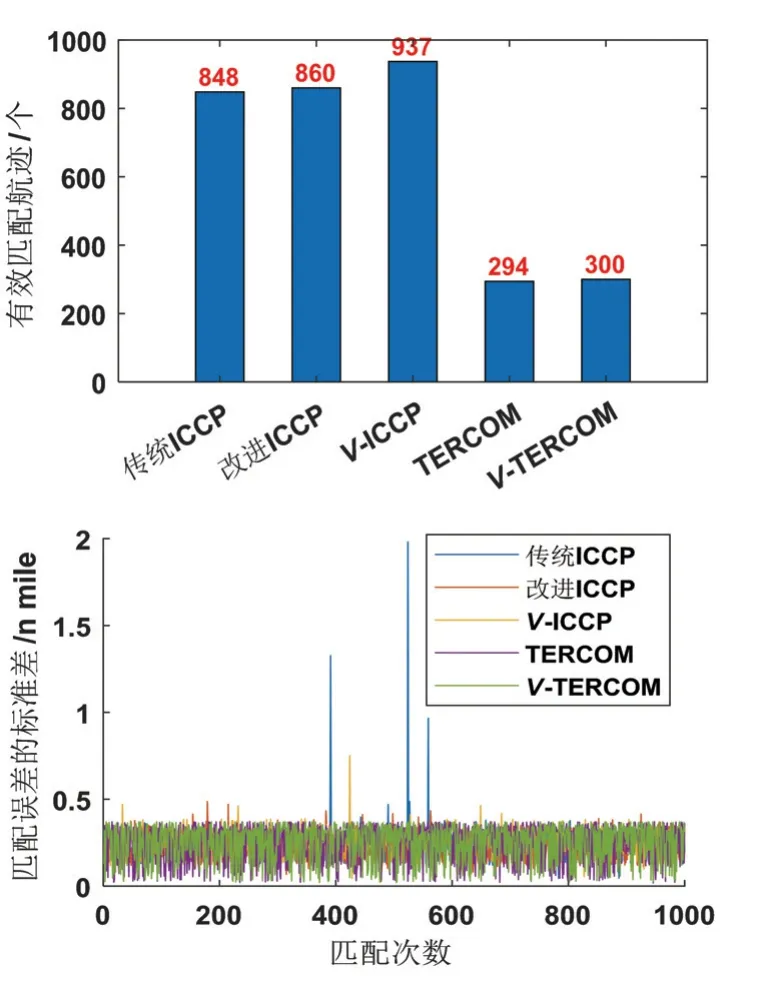
图13 航迹3 匹配结果统计Fig.13 Matching results statistics of path 3

结合图11-13 可以看到，随着航迹上重力异常变化程度的增加，不同算法对应的有效匹配率均相应增大，并且本文所提方法均不同程度地增大了算法的有效匹配率。

4 结论

本文提出了一种基于地轴投影的二维重力匹配导航方法，通过建立二维重力异常数据库，利用惯导提供的纬度信息将重力仪测得的重力异常信息进行分解，提出了二维重力匹配的V-ICCP 和V-TERCOM 算法。试验结果表明，在重力异常变化程度不同的背景区域，V-ICCP 算法的有效匹配率较ICCP 分别提高了13.5%、15.1%和 8.9%，平均提高 10%以上。而TERCOM 算法受限于轨迹重力异常值的序列一致性，容易在某匹配点出现较大误差造成有效匹配率低[20]，因此本文所提V-TERCOM 算法的改善效果有限。总的来说，本文所提方法实现了不增加限制条件基础上的二维重力匹配，并提高了匹配精度和可靠性，为重力匹配问题提供了一种新的思路，在工程实际中有较好的应用价值。

此外，该方法并不限于应用在TERCOM 和ICCP两种序列匹配算法中，事实上，该方法可以广泛应用于大多数序列匹配和单点匹配算法中，这也是接下来需要重点关注的研究内容。