火灾对钢筋混凝土简支梁破坏形式的影响

张峥

(山东建筑大学 土木工程学院，济南 250101)

0 引 言

在火灾等高温作用后，建筑构件的材料性能和内部应力状况会发生变化，从而导致整体结构力学性能降低，严重影响建筑物的安全性。但是，经历火灾的建筑一般不会被立即拆除，而是希望经过修复加固后继续投入使用，因此研究火灾后钢筋混凝土简支梁的破坏形式具有重要意义。钢筋混凝土梁的火灾试验成本过高且伴随许多不可预计的危险，因此本文采用简化计算公式分析火灾后钢筋混凝土梁的破坏形式，为火灾高温后的结构安全鉴定和加固设计提供参考。

目前，国内外相关学者对常温和高温后钢筋混凝土梁开展一系列实验研究，并取得一定的研究成果。徐玉野等[1]进行高温后钢筋混凝土简支梁静载试验，探讨受火时间、剪跨比等参数对火灾作用后梁受剪承载力的影响规律。许清风等[2]对三面受火的受弯试件进行试验，研究保护层厚度和截面尺寸对试件火灾后剩余承载力的影响。ELLINGWOOD等[3]对钢筋混凝土简支梁进行抗火试验，发现混凝土对温度的变化不敏感，并据此建立火灾后钢筋混凝土梁的数学模型。张大长等[4]分析RC、PC构件材料的高温性能，提出火灾后钢筋的强度折减公式。徐彧等[5]在考虑温度和冷却条件的影响下对混凝土进行强度试验，建立高温作用后混凝土强度的数学公式。梁兴文等[6]根据梁剪压区混凝土的压剪强度准则和斜截面平衡条件，建立梁斜截面受剪承载力数学公式。杨建平等[7]通过合理假定提出一种钢筋混凝土受弯构件高温承载力的简化计算方法。

部分学者研究火灾后钢筋混凝土梁的力学性能。张威振[8]对火灾作用后的钢筋混凝土梁进行试验，建立梁三面受火场理论计算模型，探讨升温时间和配筋率对高温后梁剩余承载力的影响。廖艳芬等[9]利用Ansys模拟三面受火时钢筋混凝土梁构件的内部传热和变形过程，得到构件应力变化和结构变形随火灾发展的规律。姜封国等[10]对构件的三面受火瞬态温度场进行计算，验证三面受火温度场简化计算的可行性，并在此基础上提出一种火灾后梁剩余承载力的计算方法。LIN等[11]开发一种非线性有限元分析程序，研究不同钢筋类型和混凝土保护层厚度的FRP筋混凝土梁的耐火性能，发现FRP筋混凝土梁耐火性能随混凝土保护层厚度的增加而提高。

钢筋混凝土梁应用广泛,但针对三面受火钢筋混凝土梁的研究较少，因此本文以三面受火钢筋混凝土梁为例，采用Abaqus软件模拟钢筋混凝土简支梁截面的温度场，对梁截面的300、500和800 ℃等温线进行等效截面简化，利用高温后梁承载力简化公式，分析混凝土保护层厚度和混凝土强度对高温后钢筋混凝土简支梁破坏形式的影响。

1 钢筋混凝土梁简化分析过程

1.1 建模分析

采用有限元软件Abaqus对截面尺寸250 mm×400 mm的钢筋混凝土梁建立三面受火温度场模型，梁尺寸和截面配筋示意见图1。

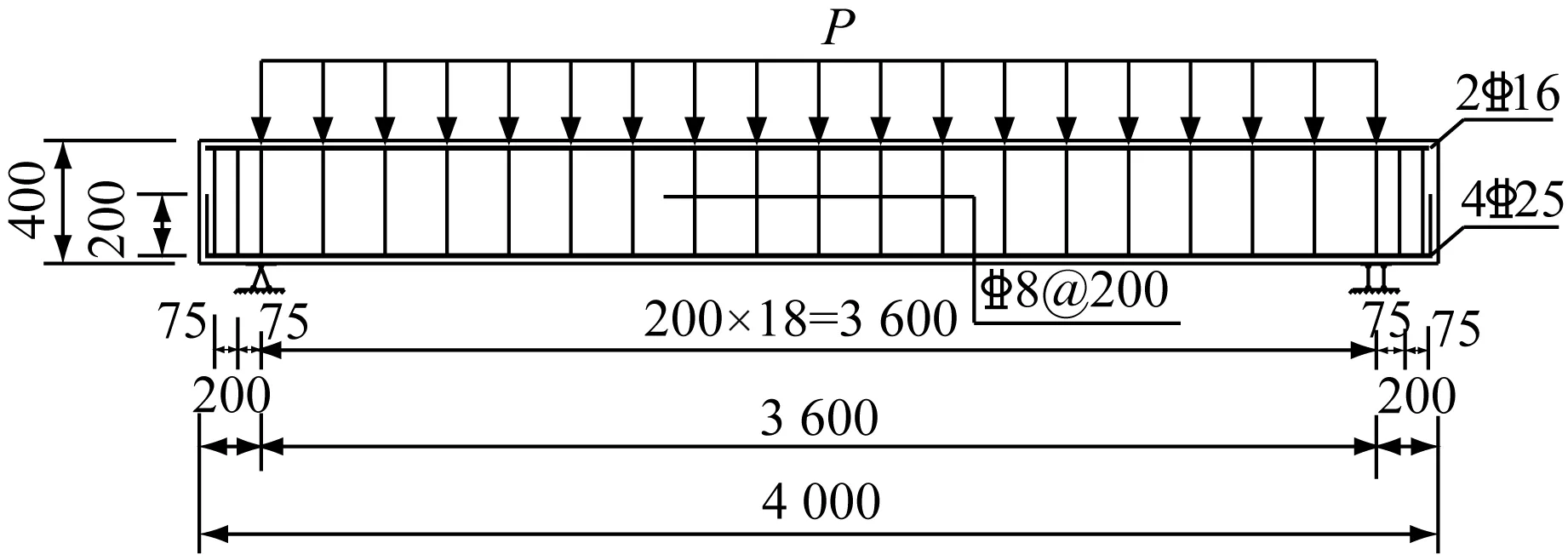
(a)梁尺寸

1.2 温度场模型的建立及分析

在火灾作用下，钢筋混凝土梁进行非线性瞬态传热，因此传热分析采用能量平衡方程和傅里叶定律，

(1)

根据文献[11]，混凝土和钢材的热传导系数λ、比热容c、密度ρ等热工参数均采用欧洲规范。混凝土选择为实体、匀质截面类型，钢筋设定为桁架截面类型。受火面采用第三类边界条件，其对流换热系数取25 W/(m·℃)；非受火面采用第一类边界条件，其对流换热系数取9 W/(m·℃)。

采用结构化网格划分技术，网格尺寸设定为20 mm。在保证网格划分、节点编号不变的基础上，采用8节点线性传热实体单元DC3D8模拟混凝土，采用2节点传热连接单元DC1D2模拟钢筋，钢筋和混凝土之间采用Tie约束。

所有钢筋混凝土梁均采用三面受火形式，初始环境温度定义为20 ℃，采用ISO 834标准升温曲线[12]，持续加热时间为3 h。温度场模拟模型见图2。

(a)网格划分

1.2.1 温度场的截取和验证

火灾环境对钢筋混凝土梁沿长度方向的作用不大，不考虑钢筋传热[13]时对构件进行温度场计算，可将三维热传导问题简化为二维平面热传导问题。每隔5 min取一次载荷作用处的梁截面(NT11)温度图，不同受火时间的截面温度分布云图见图3。

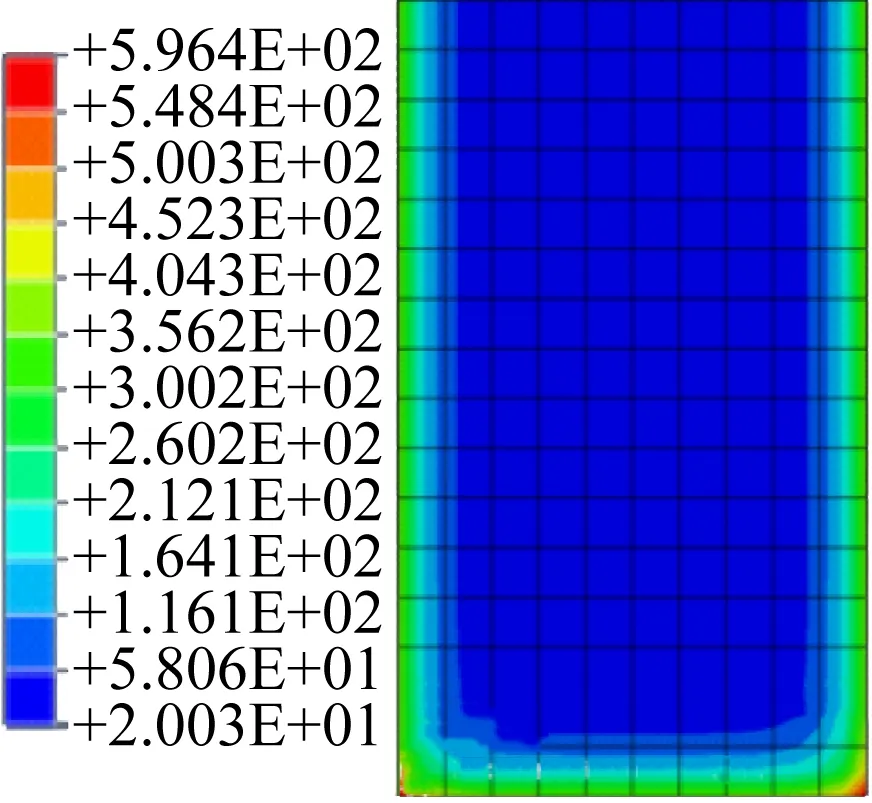
(a)受火600 s

为计算火灾高温作用后钢筋混凝土梁的极限承载力，选取左侧2根受拉钢筋(纵筋a和b)、左侧受压钢筋(纵筋c)和多个箍筋分布位置作为参考点，得到不同时刻钢筋温度的变化曲线，见图4。对比试验实测温度和参考点模拟温度，两者吻合较好，证明采用Abqus模型模拟火灾后温度场的可靠性。

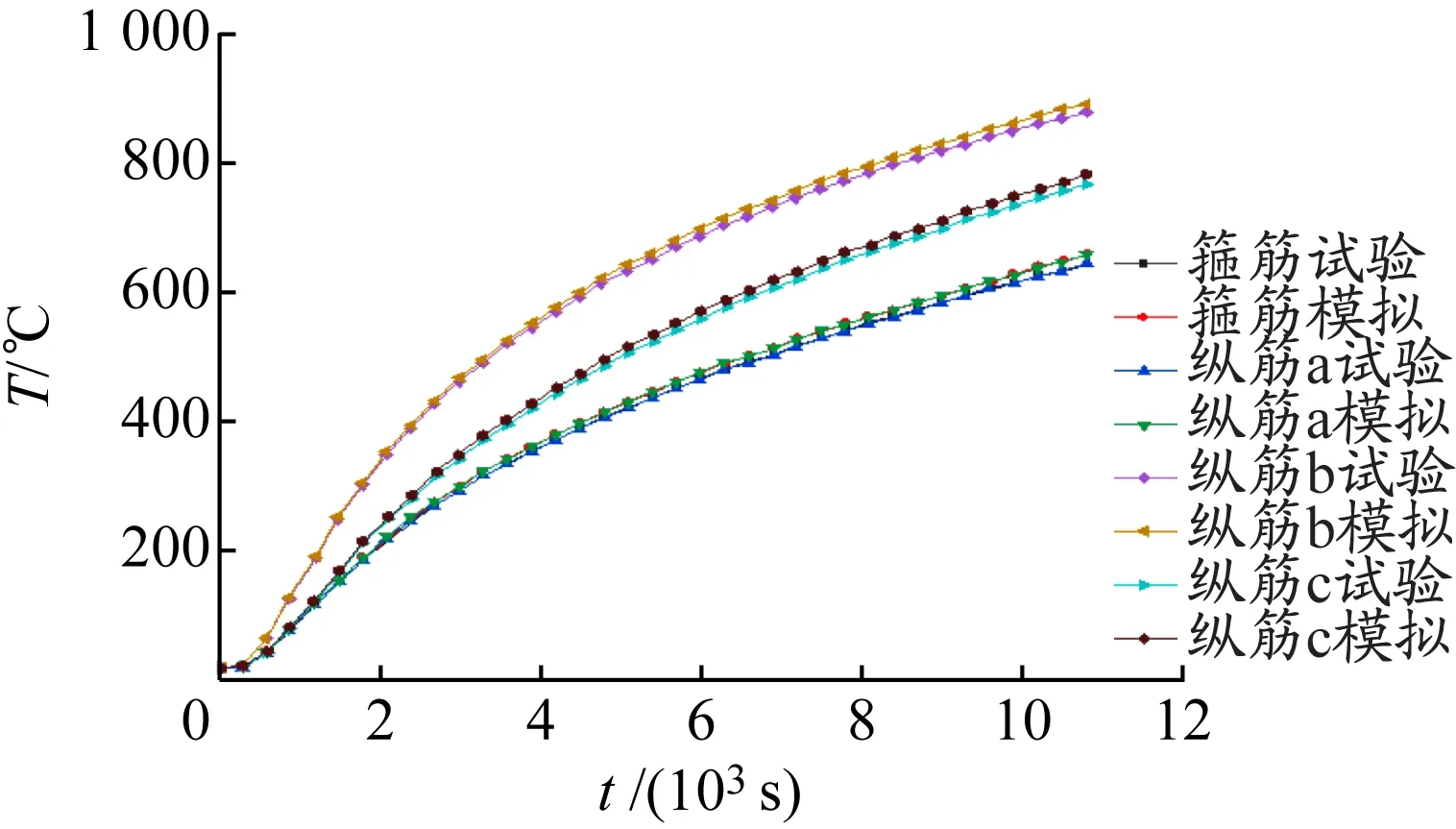
图 4 钢筋温升曲线

1.2.2 等温截面的简化

采用Abaqus分析三面受火梁温度场，确定不同受火时间梁截面的300、500和800 ℃等温线，并采用等效截面法对构件进行简化。当构件三面受火时，在自然降温情况下，截面简化计算规则为：温度300 ℃及以下的部分，取其截面的所有面积；温度高于300 ℃不超过500 ℃的部分，取其面积的0.7倍；温度高于500 ℃不超过800 ℃的部分，取其面积的0.3倍；温度高于800 ℃的部分，其截面面积可忽略不计。梁的等温截面简化示意见图5。

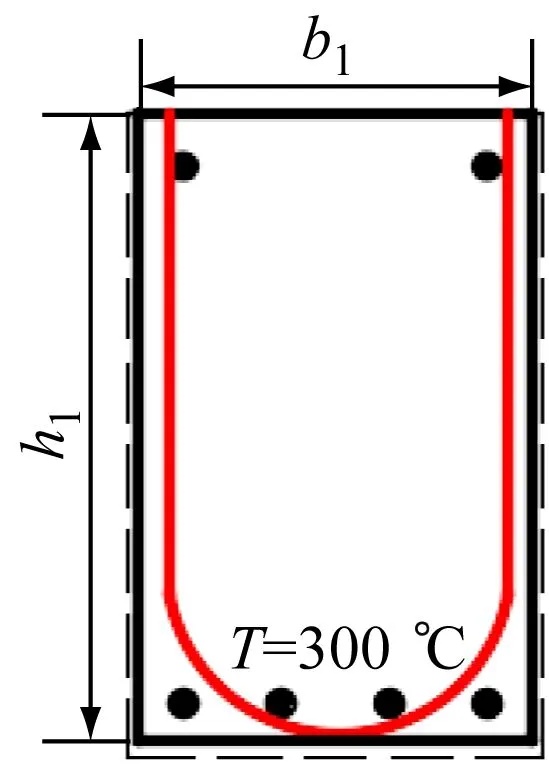
(a)受火时间600 s

1.3 高温后结构的力学性能

1.3.1 高温后钢筋的力学性能

(2)

式中：fy,T为高温后的钢筋强度标准值；fy为常温下钢筋的强度标准值；T为温度,℃。

1.3.2 高温后混凝土的力学性能

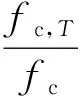
(3)

式中：fc,T为高温后混凝土的强度标准值；fc为常温下混凝土的强度标准值。

1.4 极限承载力计算公式

1.4.1 常温下极限承载力计算公式

构件极限受剪承载力计算选用文献[7]中的斜截面受剪极限承载力公式

(4)

式中：λ为计算截面的剪跨比；b为截面宽度，mm；h0为截面有效高度，mm；Asv为截面配置在同一截面内箍筋各肢的全部截面面积和，mm2；S为截面沿构件长度方向的箍筋间距，mm。

极限受弯承载力采用《混凝土结构设计规范》[15]中正截面受弯承载力的1.1倍，即

(5)

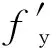
1.4.2 高温后极限承载力计算公式

高温作用使混凝土和钢筋的强度均受到不同程度的劣化，因此在计算高温后钢筋混凝土梁承载力时，应考虑混凝土强度和钢筋强度的折减。根据文献[13]和[16]，高温后受剪极限承载力简化计算公式为

(6)

式中：b1为等效截面宽度，mm；h1为等效截面有效高度，mm。

借鉴文献[14]，高温后受弯极限承载力(弯矩)

(7)

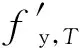
2 计算验证

2.1 试验现象验证

根据文献[14]中的试验，对相同尺寸配筋的钢筋混凝土梁分别进行常温极限载荷试验和经历火灾作用后直接加载试验，试验梁长度为4 m，截面尺寸为250 mm×400 mm，混凝土强度等级为C30，混凝土保护层厚度为25 mm，钢筋强度等级HRB400，均布载荷(见图1)。试验结果表明：在常温下分级加载，试件的最大均布载荷P为163.8 kN时，对应承受的弯矩为265.5 kN·m，破坏形式为剪切破坏；火灾作用2 h后，施加的最大均布载荷为149.9 kN，对应的弯矩为142.8 kN·m，最后的破坏形式为弯曲破坏。

利用式(4)和(5)，可以计算得到该梁在常温下的极限承载力V=271.6 kN、弯矩M=284.15 kN·m。利用式(2)～(7)，可以计算得到受热时间为2 h时梁的极限承载力VT=205.5 kN、弯矩MT=135.94 kN·m。

梁在常温下发生受剪破坏，在高温后发生弯曲破坏，理论计算结果与试验现象吻合，说明上述公式可以较准确地反映试件的承载力极限值。

2.2 高温后钢筋混凝土梁的破坏模式变化规律

为探究梁在高温后的破坏变化规律，每5 min取一次等温简化截面，每5 min进行一次极限受剪承载力与极限受弯承载力计算，结果见表1。可知，随着受火时间增加(温度升高)，梁的极限受弯承载力和极限受剪承载力逐渐下降。

高温火灾作用后梁不同受火时间的理论极限承载力与施加载荷的比值α随时间t的变化曲线见图6。由此可知，经历火灾高温作用后，梁的极限承载力明显下降，即火灾高温作用导致梁承载能力劣化。常温下(即t=0时)梁具有明显的剪切破坏特征，而受火作用后的梁发生弯曲破坏，理论计算与试验得到的破坏形式相吻合。为方便探索破坏规律，将弯曲破坏主导和剪切破坏主导的临界点,即曲线的交点定义为ζ点。

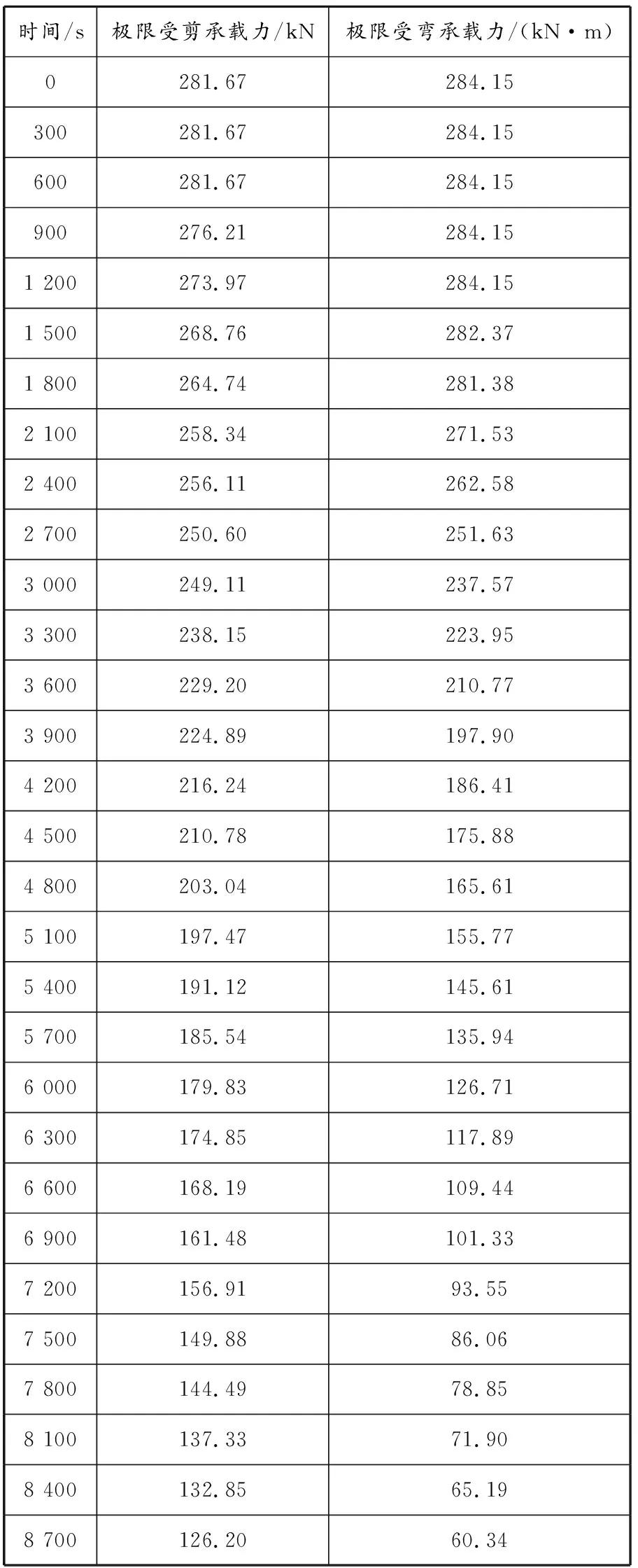
表 1 不同受火时间梁的极限承载力

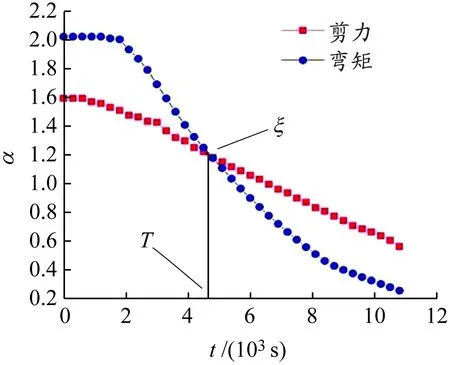
图 6 梁受火破坏的α-t曲线

3 理论分析

3.1 混凝土保护层厚度的影响

根据混凝土保护层厚度不同，设计6根试件，探究其破坏模式变化规律，混凝土强度等级取C30，试件的保护层厚度c分别为25、30、35、40、45和50 mm，不同混凝土保护层厚度试件的α-t曲线见图7。随着保护层厚度的增加，临界点ζ明显滞后。

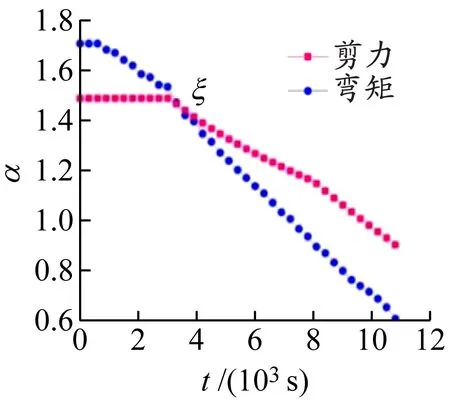
(a)c=25 mm

3.2 混凝土强度等级的影响

根据混凝土强度等级不同，设计4根试件探究其破坏模式变化规律，混凝土保护层厚度为40 mm，试件的混凝土强度等级分别为C35、C40、C45、C50。不同混凝土强度试件的α-t曲线见图8。混凝土强度等级会极大影响试件的破坏模式，随着混凝土强度增大，临界点ζ急剧延后。

4 结 论

采用有限元软件Abaqus对高温后钢筋混凝土简支梁进行模拟，通过截面温度图确定简化计算截面，结合钢筋混凝土梁高温后的简化计算公式，计算得到构件在高温后不同时刻的理论极限承载力。分析高温后钢筋混凝土梁理论计算极限承载力与施加载荷的比值，对比计算结果与试验结果，得到火灾过程中钢筋混凝土简支梁的破坏模式变化规律，主要结论如下：

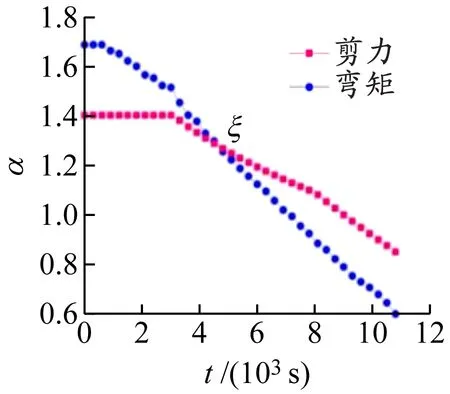
(a)C35

(1)本文建立的有限元模型能较好地模拟高温中钢筋混凝土梁的破坏特征，相关参数设置可以为类似有限元模拟提供参考。

(2)本文提出的钢筋混凝土梁高温后的简化计算公式简便，计算结果与试验结果误差较小，可以为高温中钢筋混凝土梁承载力提供参考。

(3)随着混凝土保护层厚度和混凝土强度等级的增加，构件受剪破坏和受弯破坏变化的临界点ζ发生明显滞后，其中混凝土强度等级对临界点ζ滞后的影响尤为明显。