FFT幅相联合的快速高精度频率估计方法

马罗文，刘宁，胡心语，倪丽花

（1.中国人民解放军95865部队，北京 102200；2.中国人民解放军32802部队，北京 100082；3.电子科技大学，四川 成都 611731）

0 引言

在雷达［1-3］、通信［4-5］、声呐［6］等领域对信号频率进行快速、准确的测量具有重要意义。目前，常用的频率估计算法按照工作原理可以分为：计数法、相位法、快速傅里叶变换算法、子空间分解类算法等。其中，单频信号［7］的估计问题一般采用计数法和相位法；而多频信号估计问题一般采用的方法为子空间分解类算法和快速傅里叶变换算法。子空间分解类算法［8-9］中典型代表为多重信号分类（Multiple Signal Classification，MUSIC）算法［10］和旋转不变技术估计信号参数（Estimating Signal Parameter Via Rotational Invariance Techniques，ESPRIT）算法［11］，此类子空间分解算法具有较高的估计精度，但由于需要搜索幅度谱峰值位置或特征值分解导致计算量相对较大。快速傅里叶变换算法［12］只能对有限点序列进行处理，会造成能量泄露，同时存在栅栏效应，当信号频谱峰值谱线不能与主瓣的中心重合时，信号真实频率落于主瓣内的两根谱线之间，便会产生较大的频率测量误差［13-16］。

由于快速傅里叶变换的幅度谱频率搜索间隔与信号采样数或快速傅里叶变换的长度成反比，为了降低快速傅里叶变换法幅度谱频率搜索间隔的量化误差对频率测量精度的影响，常采用填零的方法增加信号采样数或快速傅里叶变换的长度。但是，快速傅里叶变换的计算量与信号采样数或快速傅里叶变换长度成正比，这种提高测频精度的方法也会使频率测量的计算量成倍地增加，导致其难以应用于实时性要求较高的场景。

高精度和实时性要求的矛盾一直都是频率估计在高速全数字解调器中应用的瓶颈。因此，研究一种既保证高精度，又满足低计算量的频率估计算法，具有重要的应用前景［17］。本文提出同时利用信号采样的快速傅里叶变换的幅度谱峰值位置和频率搜索间隔量化误差校正值确定信号频率的方法，能实现高精度快速测频的目的。

1 信号模型

暂不考虑噪声时，单频复谐波信号表示为

式中：A为复正信号的幅度；f0为频率，Hz；θ0为初相，rad。在不做特殊说明的情况下，本文基于该信号展开算法理论推导与实验分析。

经过N点采样后的离散信号表示为

对x(n)进行N点快速傅里叶变换，得到

幅度最大值处的离散频率索引值为m，根据X[k]幅度最大值处的位置m可以得到信号频率的估计值为由于栅栏效应的存在，当信号频谱峰值谱线不能与主瓣的中心重合时，信号真实频率落于主瓣内的两根谱线之间，便会产生较大的频率测量误差。

因此，本文利用信号相位信息，消除了传统方法仅使用幅度信息受到的搜索间隔的限制，提出了FFT幅相联合的快速高精度频率估计方法。

2 FFT幅相联合的高精度频率估计方法

首先对前N-1个信号采样x(n)，n=0，1，2，…，N-2，采用快速傅里叶变换，得到频谱序列y1(k)，为

然后经过一位滑窗平移得到后N-1个信号采样x(n)，n=1，2，…，N-1，并对其采用快速傅里叶变换，得到频谱序列y2(k)，为

由于频谱序列y1(k)和y2(k)是对具有相同频率的采样信号进行FFT运算得到的，那么y1(k)和y2(k)幅度谱的峰值位置相同。根据频谱序列y1(k)和y2(k)，得到幅度谱z(k)为

根据式（6），信号频率估计值所对应的序列号，即幅度谱的谱峰位置m为

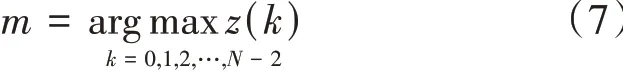
根据式（3），式（4）和式（5）在幅度谱的谱峰位置m处的比值为

FFT幅相联合的高精度频率估计f0为

式中：angle表示复数的相位角。

由式（9）可知，利用了频谱序列y1(m)和y2(m)的相位差对频率进行估计，频率的估计结果不再受限于频率搜索间隔的量化误差，从而实现高精度频率估计。

3 FFT幅相联合的快速高精度频率估计方法

根据式（4）和式（5）可知，为了求解y1(k)与y2(k)，需要进行两次N-1点FFT变换，对此，提出FFT幅相联合的快速高精度频率估计方法，利用迭代，仅需要一次FFT变换求解y1(k)，然后通过对y1(k)进行简单的加法和乘法迭代运算就可以得到y2(k)，避免了FFT变换重复计算的问题可实现快速高精度频率估计。

由式（4）和式（5）得

式中：v为信号采样的尾首样本差。

根据频谱序列y1(k)和信号采样的尾首样本差v，即可快速得到幅度谱z(k)为

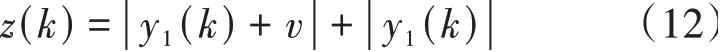
由式（7）知信号频率估计值所对应的序列号m。

进一步利用频谱序列y1(k)和y1(k)+v在幅度谱峰位置m处的相位差，消除FFT算法受限于量化间隔的影响。根据式（8）和式（10），在幅度谱的谱峰位置m处，可以得到

频率搜索间隔的量化误差校正值u为

得到FFT幅相联合的快速高精度频率估计f0为

上述算法流程图如图1所示。

图1 FFT幅相联合快速高精度算法流程图Fig.1 Flow chart of fast high precision algorithm based on FFT amplitude and phase combination

综上，FFT幅相联合的快速高精度频率估计算法，一方面通过使用滑窗迭代算法，只需要进行一次FFT变换就可以得到频谱序列y1(k)和y2(k)，减少了冗余计算；另一方面，利用幅度谱峰y1(m)和y1(m)+v的相位差对频率搜索间隔量化误差进行校正，达到了高精度快速测频的目的。

4 计算复杂度分析

为了求解y1(k)与y2(k)，需要进行2次N-1点FFT变换，计算复杂度为

由式（10）可知，通过一次FFT变换求解y1(k)，然后对y1(k)进行简单的加法和乘法迭代运算就可以得到y2(k)，从而避免了FFT变换重复计算的问题，因此，与传统FFT算法相比，本文所提的FFT幅相联合的快速高精度频率估计算法的计算复杂度节省了O((N-1)log(N-1)-2)，从而实现快速高精度频率估计。

5 仿真结果与分析

为了验证FFT幅相联合的快速高精度频率估计算法的性能，进行多次蒙特卡洛仿真实验，并与经典的FFT算法进行比较。测量信号频率时，FFT算法只利用幅度谱的谱峰位置测量信号频率，FFT幅相联合的快速高精度频率估计算法不仅利用了幅度谱的谱峰位置，还利用了频率搜索间隔的量化误差校正值。

仿真过程中，信号采样数分四种情况，即N=32，64，128，256，信号采样中包括归一化频率（相对于采样频率）等于0.2140，信噪比为18 dB的信号，以及归一化频率等于0.1070、干信比为11 dB的干扰。

当N=32，64，128，256时，频谱序列y1(k)和y2(k)的幅度谱及其相位如图2至图5所示。可见，频谱序列y1(k)和y2(k)的幅度谱y1，y2的谱峰位置相同，验证了通过式（6）估计谱峰位置是合理的；且随着采样点数增加，这一个特征越明显。

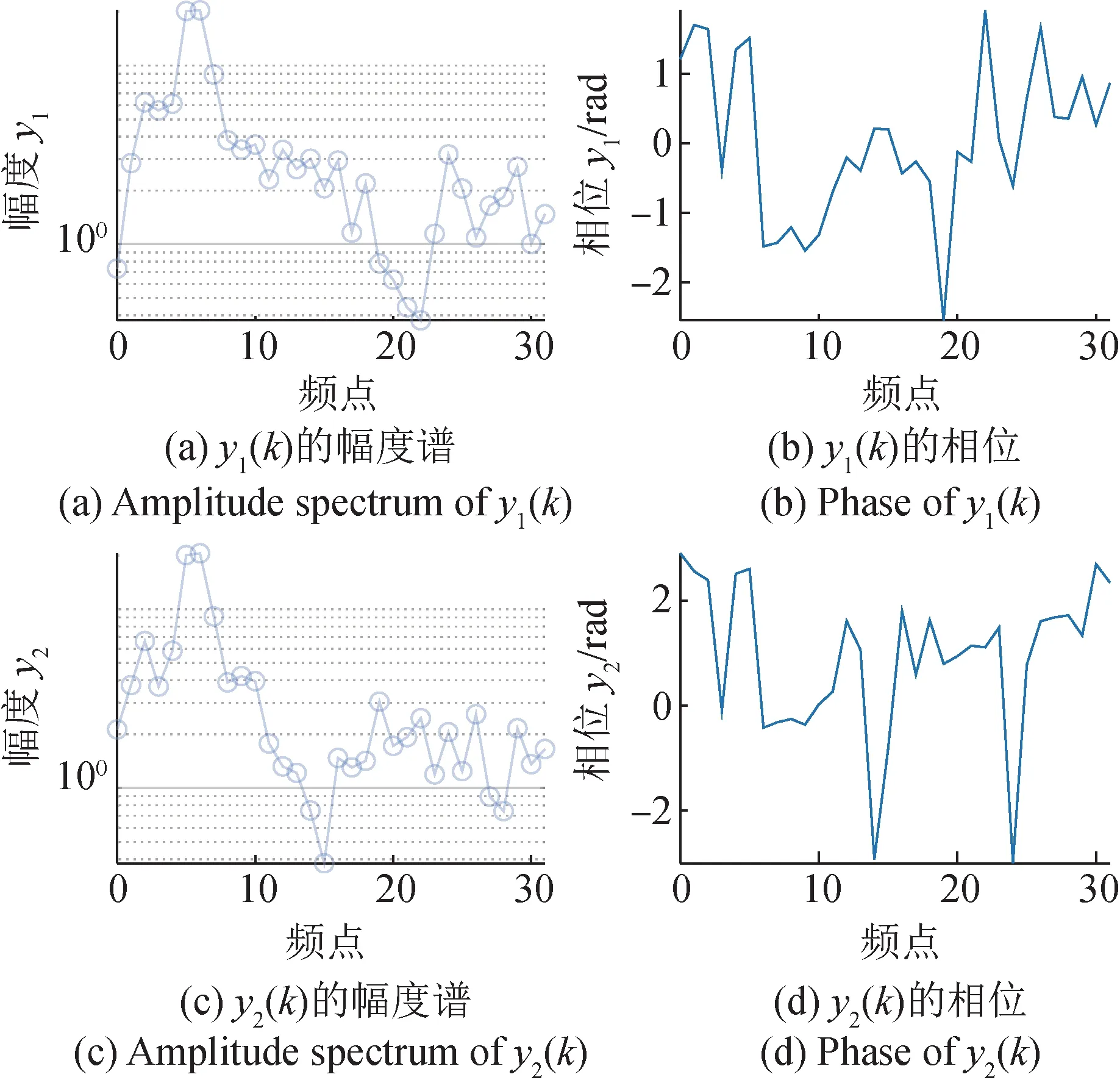
图2 N=32时，y1(k)和y2(k)的幅度谱及相位Fig.2 Amplitude spectrums and phases of y1(k)and y2(k) for N=32

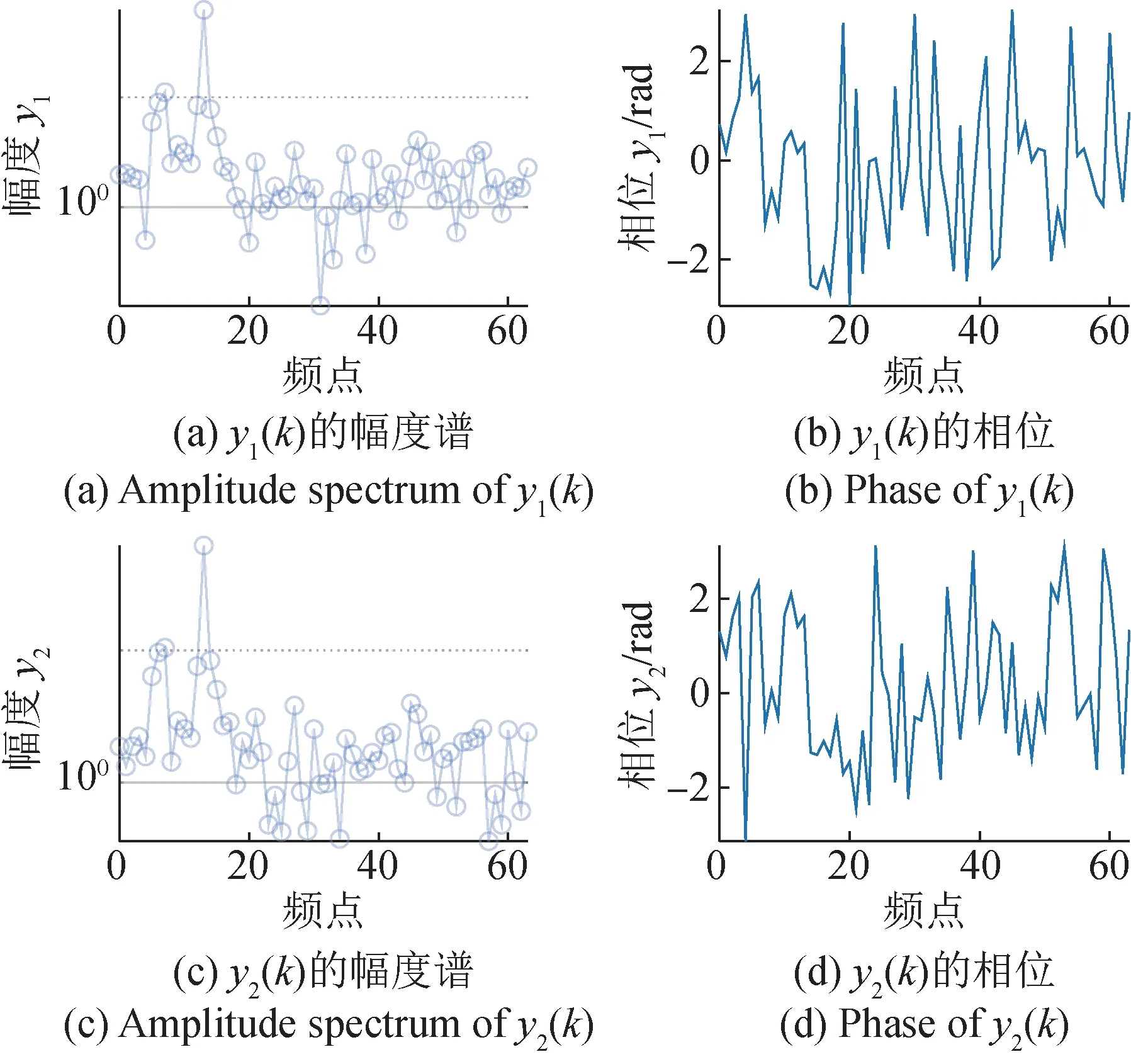
图3 N=64时，y1(k)和y2(k)的幅度谱及相位Fig.3 Amplitude spectrums and phases of y1(k)r and y2(k) for N=64

图5 N=256时，y1(k)和y2(k)的幅度谱及相位Fig.5 Amplitude spectrums and phases of y1(k)and y2(k) for N=256

当N= 32，64，128，256时，FFT算法与FFT幅相联合的快速高精度频率估计算法的信号归一化测频均方根误差的累计概率分布函数（CDF）如图6所示。可见，FFT幅相联合的快速高精度频率估计算法在信号采样数N= 32时的CDF接近FFT算法在信号采样数N= 256时的CDF，达到了高精度测频的目的。

图4 N=128时，y1(k)和y2(k)的幅度谱及相位Fig.4 Amplitude spectrums and phases of y1(k)and y2(k) for N=128

图6 不同采样数，FFT算法与FFT幅相联合快速算法的归一化测频误差的CDF及局部图Fig.6 CDFs of normalized frequency measurement error of FFT algorithm and fast FFT amplitude and phase combination algorithm with different sampling numbers

由仿真结果可见，不同采样数下，FFT算法的信号归一化测频均方根误差分别为0.0091，0.0044，0.0023和0.0011；FFT幅相联合的快速高精度频率估计算法的信号归一化测频均方根误差分别为0.0014，0.0007，0.0003和0.0002。可以得出，与FFT算法相比，利用同样的采样信号，当N=32，64，128，256时，FFT幅相联合的快速高精度频率估计算法的归一化均方根误差分别降低了84.15%，84.57%，85.24%和84.73%，FFT幅相联合的快速高精度频率估计算法在信号采样数N=32时的测频精度接近FFT算法在信号采样数N=256时的测频精度，达到了高精度测频的目的。

6 结论

本文提出了一种FFT幅相联合的快速高精度频率估计算法，一方面，只需要进行一次FFT变换就可以得到两个频谱序列，从而减少了冗余计算；另一方面，利用两个频谱序列的相位差对频率搜索间隔量化误差进行校正，达到了高精度快速测频的目的。实验结果和分析表明，由于同时利用了幅度谱的谱峰位置与频率搜索间隔的量化误差校正值，该算法在信号采样数N=32时的测频精度接近FFT算法在信号采样数N=256时的测频精度，适用于需要快速、高精度测频的应用场合。未来的研究还可以利用更多的频谱序列，进一步提高频率估计的精度。