横向异种类型混合桥面设计方法

戴昌源

[上海市政工程设计研究总院（集团）有限公司，上海市200092]

0 引 言

在多车道桥梁中，不同车道行驶的车辆类型与轴重有较大差异。以目前较为普遍的双向6车道为例，根据杭州湾大桥一个月的动态称重（WIM）数据，轴重超过48 t的车辆中有58%行驶在慢车道，中间车道此类车辆占比41.4%，而内侧车道仅占0.6%；文献[1]给出了青马大桥12 a的WIM数据，统计数据表明中间车道车流量最大，内侧和外侧车道车流相当，高峰时段单位时间内通过外侧车道的车辆总轴重是中间车道的3倍，是内侧车道的约10倍。外侧车道在重载车辆的反复作用下是疲劳破坏较为严重的区域。文献[2]对南京长江三桥运营近20 a时间后正交异性钢桥面产生的疲劳裂缝进行统计，共发现998处疲劳裂缝，其中有57%分布在慢车道范围内。

相比正交异性钢桥面，研究表明超高性能混凝土（UHPC）华夫板和超高性能混凝土（UHPC）组合板的疲劳性能较为优异[3-5]，在重车道（亦可包括中间车道）采用疲劳性能更优的UHPC华夫板和UHPC组合板，在快车道（亦可包括中间车道）仍采用传统的正交异性钢桥面，组合成混合桥面形式，在满足桥面承载、传力以及疲劳性能要求的同时，可以有效降低结构自重、提升结构材料的利用效率。两种不同类型的桥面连接的位置可设置一个接缝构造以使两种不同种类的桥面可以更好地协同受力。

目前国内外的规范中对桥面的设计方法仅针对同一种桥面类型，较少有对不同种桥面混合后设计计算方法的规定。在混合桥面中两种不同类型的桥面的各方向抗弯刚度等参数有较大不同，荷载作用下内力的分配以及等效后的有效宽度等设计参数不同于单一类型的桥面。为了明确混合桥面各部分协同受力机理，采用梁格模型对混合桥面进行了变参分析，分析了接缝、桥面各部分承担荷载比例与有效宽度的影响因素，并拟合了上述二者的计算公式，并基于此提出了混合桥面的设计方法。

1 参数化分析模型

限于篇幅，这里以采用UHPC华夫板的混合桥面为例进行参数化分析，分析模型构造如图1所示，虚线为划分梁格的位置。由于参数化分析需对大量的模型进行分析并提取结果分析整理，为了提高分析效率与稳定性，采用ANSYS参数化建模语言APDL建立混合桥面梁格模型，将桥面跨度、华夫板纵横肋间距和板厚、接缝T肋高度等设为可变参数，便于批量生成分析模型，模型纵梁一般断面如图2所示。

图1 华夫板混合桥面模型（单位：mm）

图2 梁格模型纵梁断面

加载工况如图3所示，分为正弯矩加载和负弯矩加载两种情况。

图3 加载工况（单位：mm）

2 各部分承担荷载比例

2.1 参数取值

参数的取值如表1所示，参数的默认取值为跨度4 m、横肋间距540 mm、纵肋间距500 mm、板厚210 mm、纵向接缝T肋高度400 mm，每次仅变化一个参数的取值，除变化参数外的其余参数按照默认值取，总计58个模型。

表1 参数取值

2.2 分析结果与回归分析

分析结果表明，当荷载作用于华夫板部分时荷载主要由纵向接缝部分和华夫板部分承担，只有很少比例传递到正交异性钢板部分（1%左右）。同样，当荷载作用于正交异性钢板部分时只有很少比例传递到华夫板部分。这是由于正交异性钢板纵向抗弯刚度远大于横向抗弯刚度导致。因此当荷载作用在正交异性钢板上时可按现行规范规定的方法对正交异性钢板进行第二体系设计，而荷载作用于华夫板部分时需要明确华夫板部分与纵向接缝部分各自承担的荷载大小才能进行第二体系设计。篇幅所限，给出了两个影响较为显著的因素：横梁间距和桥面板跨度对接缝部分承担荷载比例的影响，如图4、图5所示。

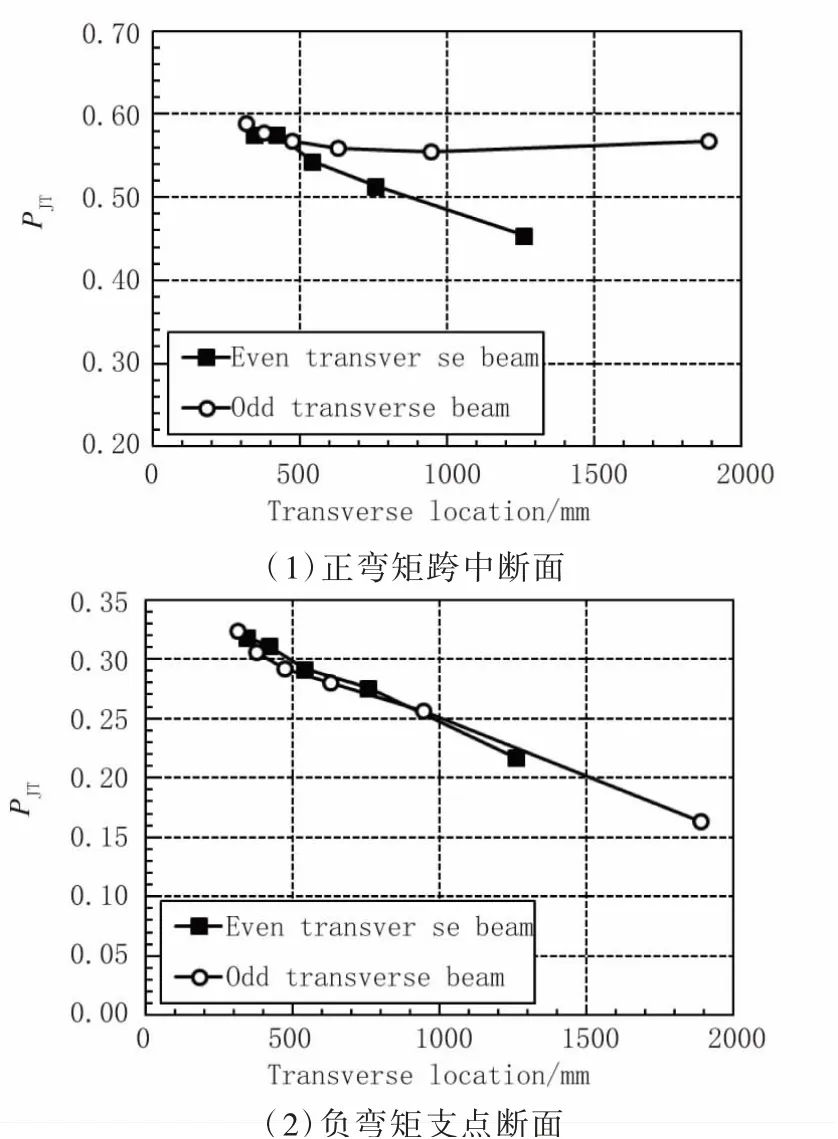
图4 接缝所承担荷载比例随横梁间距的变化规律（单位：mm）

从图4可以看出，随着横肋间距的增加，纵向接缝承担的荷载比例降低，华夫板部分承担的荷载比例上升，这是由于横肋间距增加导致单位长度华夫板横向弯曲刚度降低。图5表明纵向接缝承担荷载比例随桥面板跨度的增加而增加，而华夫板承担荷载的比例逐渐减小。

图5 接缝所承担荷载比例随桥面板跨度的变化规律（单位：mm）

采用多项式拟合的方法对上述分析数据进行回归分析。采用接缝与华夫板部分的抗弯惯性矩之比β=Ijt/Iwf、跨度L、横向单位宽度抗弯惯性矩J=Iwfl/b三个参数作为回归分析的变量。同时考虑上述参数的二次项和常数项C，共计有10个变量。表达如式（1）：得到纵向接缝承担荷载的比例PJT的计算公式，正弯矩区如式（2）所示，负弯矩区如式（3）所示（单位：m）。华夫板部分承担的荷载比例可通过1-PJT计算得到。

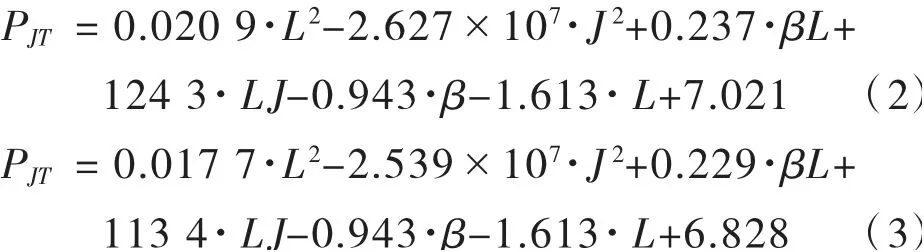
3 桥面板有效宽度

有效宽度的概念可以极大的简化板构件的设计，使其可以按照梁构件的设计方法进行设计。本节将基于前述58组梁格模型探讨混合桥面华夫板部分在活载作用下的横向和纵向有效宽度的影响因素和简化计算公式。首先对桥面板有效宽度we做如下定义：

其中：S为梁格模型中一根华夫板纵梁的截面的宽度；Mi为梁格模型中第i根华夫板纵梁的弯矩；n为华夫板纵梁的根数；Mmax为华夫板纵梁弯矩的最大值。

通过上述参数分析结果可以得到华夫板部分的有效宽度与两个主要影响参数：横梁间距和桥面跨度之间的变化关系，如图6和图7所示。可以看出对于正弯矩断面，华夫板部分的有效宽度随横梁间距的增加先增加后减小，而对于负弯矩断面则呈单调递减的趋势。当跨径增加时华夫板部分有效宽度逐渐增加，但增加速率逐渐减小。

图6 横向有效宽度随横梁间距的变化规律（单位：mm）

图7 横向有效宽度随桥面板跨度的变化规律（单位：mm）

对分析数据进行拟合，得到华夫板部分桥面有效宽度的计算公式，正弯矩区如式（5）所示，负弯矩区如式（6）所示（单位：m）。

4 混合桥面设计方法

综上，可以归纳出混合桥面进行第二体系设计的设计思路，如图8所示。总体分为两步，首先确定第二体系的设计荷载，恒载按照传统求解连续梁弯矩的方法即可得到，活载设计值的计算可通首先确定车辆荷载作用下整个桥面断面的第二体系总弯矩，再通过前述荷载比例计算公式计算华夫板各部分承担荷载的比例即可得到混合桥面各部分的活载内力设计值。最后进行断面的第二体系承载能力验算，计算断面的有效宽度，此后即可按照现行规范的设计方法对混合桥面各主要组成部分进行设计。这里虽然以UHPC华夫板混合桥面为例，但此方法同样适用于其他横向由两种类型桥面构成的混合桥面的设计。

图8 混合桥面设计流程

5 结 语

本文以UHPC华夫板混合桥面为例通过参数化梁格模型分析了桥面板跨度、横、纵肋间距、接缝T肋高度、桥面板厚度等参数对混合桥面各部分承担荷载比例和华夫板有效宽度的影响。

（1）通过回归分析得到了UHPC华夫板混合桥面中各部分承担荷载比例和华夫板有效宽度的计算公式。

（2）提出了一种对横向由两种类型桥面构成的混合桥面的设计方法。