基于在线极限学习机的配电网无功电压控制

王元元，孙名妤，司君诚，张双乐，蔡言斌

（国网山东省电力公司东营供电公司，山东 东营 257506）

0 引言

配电网无功优化是通过控制无功设备的无功出力实现无功潮流的最优分布，从而减少系统有功损耗和提升系统电压水平［1-3］。传统无功优化计算依赖于配电网设备无功-电压特性以及电网的网络拓扑结构，当电网结构或者运行场景发生变化时可能导致系统优化不收敛的现象。特别是新型电力系统框架下，电网中存在大量柔性可控资源，此时电网无功优化问题由于控制变量的增多变得更加复杂，传统无功优化算法由于其求解过程对初始值敏感等特点，在处理复杂电网的无功优化问题时，容易陷入局部最优解，造成在线无功优化控制的困难和不足。

随着人工智能技术的发展，数据挖掘以及深度学习技术在各个领域的应用不断涌现。配电网电压、电流等运行数据反映了配电网在不同场景下内部元件间的本质的耦合关系，从数据的角度挖掘电网网络结构、运行状态以及控制策略之间的内在联系，从而提高新型电力系统运行的稳定性和可靠性具有重要作用［4-5］。数据挖掘技术在配电网负荷预测、分布式电源发电预测等领域具有广泛应用［6-7］，通过分析历史数据的演变过程，挖掘负荷、分布式电源时序功率的变化规律及其对配电网控制的影响，利用机器学习方法从海量数据中发现数据之间的高维隐层关系［8-9］。

近年来，数据挖掘技术在无功电压控制也有一些尝试，文献［10］利用日前无功负荷预测指导无功潮流调度，实现无功优化的目的，但该方法主要依赖精准的负荷预测且无功策略调度考虑略显不足。文献［11］基于遗传算法和支持向量机构建无功优化模型，利用遗传算法和支持向量基的特点满足无功优化计算和控制策略的制定。文献［12］提出一种基于负荷和无功优化策略匹配的无功电压控制方法，利用实时负荷和历史负荷的高相似度，选取历史优化方案的最优策略，但是在无功优化策略和负荷间的关系偏保守。文献［13］提出一种基于数据驱动的无功优化方法，借助数据挖掘技术提取电网特征数据并利用神经网络建立无功优化策略与电网运行特征的非线性映射关系。文献［14］提出图卷积神经网络的无功优化策略，对于海量数据之间的特征关联具有较好的拟合效果。文献［15］提出了一种基于数据驱动和深度置信网络的配电网无功优化方法，通过构造高维随机矩阵利用历史数据训练无功策略与系统运行场景的内在联系。文献［16］提出了含光伏的配电网无精准无功电压控制方法，构建网架节点注入功率与电压的关系，构建无功优化模型。

极限学习机（Extreme Learning Machine，ELM）是新加坡南洋理工大学黄广斌教授提出了一种前馈神经网络，其具有非线性拟合能力强，过程简单等特点。文献［17］将ELM 应用在回归预测和多类分类中，ELM 可以较精准的逼近目标连续函数，同时可以对数据不相交的区域进行分类。文献［18］提出一种基于DPSO-MKELM 的风机齿轮箱故障诊断系统，利用不同尺度小波核函数叠加极限学习机构造故障诊断模型，提高分类的精度和收敛速度。文献［19］提出一种基于在线极限学习机（Online Sequential Extreme Learning Machine，OS-ELM）的超短期负荷预测模型，借助OS-ELM的在线机制实现对短期负荷的准确预测，并利用其计算速度快的特点实现在线应用。文献［20］提出一种云计算和OS-ELM 相结合的负荷预测方法，采用云计算实时处理海量高维数据，借助OS-ELM 的在线机制，随实时数据进行自我进化，利用OS-ELM的计算能力实现优异的并行性能。

针对配电网无功优化过程中的信息不全难以精准建模等问题，提出了一种基于数据驱动的在线极限学习机的配电网无功优化方法。利用在线极限学习机对配网无功优化进行分析，通过蒙特卡洛构造系统状态和对应无功优化策略的数据集，借助在线极限学习机对系统进行理解和学习，通过学习和理解配网系统特征和无功优化策略之间的关系，建立基于在线极限学习机的无功优化模型。基于IEEE-33 节点主动配电网进行算例测试，结果显示本文方法的有效性和准确性。

1 ELM

1.1 ELM网络模型

ELM 是基于单隐含层前馈神经网络构建（Single Hidden Layer Feedforward Neural Network，SLFN）的机器学习方法，在训练过程中其随机选取输入层权重和隐藏层偏置，利用广义逆矩阵理论最小化损失函数求解输出层权重，其中损失函数由训练误差项和输出层权重范数的正则项构成。即使随机生成隐藏层节点，ELM 仍保持SLFN 的通用逼近能力，具有训练参数少、学习速度快、泛化能力强等优点。其原理如图1所示。

图1 ELM结构

ELM 模型在训练阶段采用随机的输入层权值和偏差而不是基于梯度的下降算法，通过随机选择隐藏节点、随机确定隐层权重参数和偏差，以解析计算的方式确定输出层权值。当任意的输入样本{(xp,yp)}（p=1，2，…，N）确定之后，具有隐藏层节点和激活函数的ELM模型可以表示为

式 中 ：xp∈Rn,xp=[xp1,xp2,...,xpn]T；yp∈Rm，yp=[yp1,yp2,...,ypm]T）；h(x)为激活函数；wp是输入层和隐藏层之间的权重系数；βp是用来连接隐藏层和输出层的权重系数；bp为隐含层的阈值。

ELM 训练SLFN 分为随机特征映射和线性参数求解两个阶段。

1）随机特征映射。

随机初始化隐藏层参数，采用非线性映射作为激活函数，将输入数据映射到新的特征空间。与现有传统支持向量机等算法不同，ELM 中的非线性映射函数可以是任何非线性分段连续函数，隐藏层节点参数w、b由任意连续概率分布随机生成，而不是经过训练确定，因此，其与传统神经网络相比在效率方面占很大优势。

2）线性参数求解。

ELM 学习第二阶段的目标是求解输出层的权值β。基于现有训练样本集，其用Hβ与样本标签Y求最小化平方差作为评价训练误差，从而得到具有拟合效果更佳的输出层权重β。即通过最小化近似平方差的方法对连接隐藏层和输出层的权重β进行求解，目标函数如式（2）所示。

式中：H是隐藏层的输出矩阵；Y是训练数据的目标矩阵；β=[β1,β2,...,βR]T为隐含层与输出层之间的连接权重。

对于含R个隐含层和N个样本的ELM模型表示如下：

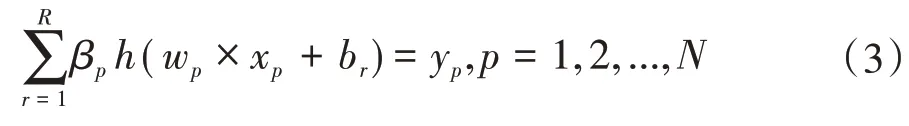
式中：Y=[y1,y2,...,ym]T为神经网络的输出；矩阵H为ELM 的隐含层输出矩阵；H+为矩阵H的Moore-Penrose广义逆矩阵。

1.2 在线序列极限学习机

OS-ELM 和标准基线学习机之间的区别在于引入在线机制不断更新输出层权重β，β更新方式随着样本数量的不同而不同，其更新方式主要分为两类：多样本更新和单样本更新。当第k批样本为多样本时，β更新迭代方式可表示为

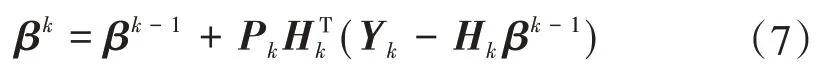
式中：Pk为H的转置与H乘积的逆，初始值P0为

Pk的更新方式为

当第k批样本为单样本时，β更新迭代方式可表示为

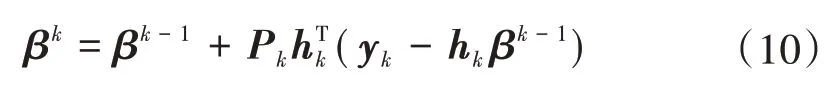
Pk的更新方式为

OS-ELM 利用新数据不断优化和更新模型参数，在历史训练数据有限的情况下，通过不断搜集系统运行数据进行模型的优化和迭代。当新数据到来，模型只需对新数据进行迭代处理，由此大大减小模型在更新过程中的数据处理量，算法能够自我更新和进化。因此，OS-ELM 在建模和优化速度和泛化能力上具有更多优势，其训练过程如图2所示。

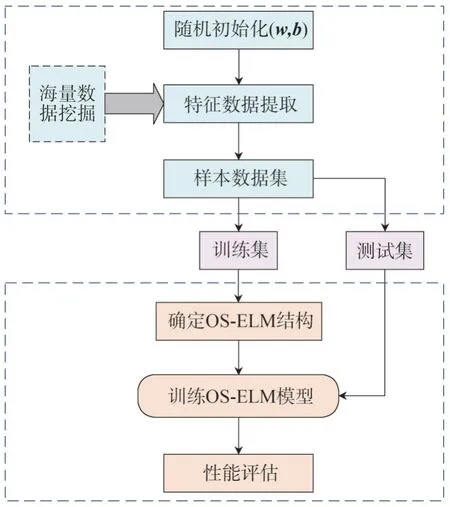
图2 OS-ELM训练过程

2 基于在线极限学习机的配电网无功优化

2.1 配电网的无功优化模型

基于数据驱动的无功优化的关键是构建配电网运行状态和对应无功调度策略的参数控制集。无功优化模型是构建在线无功优化策略的基础，通过不同运行场景下配电网无功优化，获得各运行场景下的无功控制策略，建立配电网运行场景与无功控制策略的数集，并以此作为数据驱动策略的输入和输出进行训练，获得数据驱动无功优化模型。本文以传统无功优化为基础，通过蒙特卡洛方法构建不同运行场景下的无功优化策略来获得配电网无功电压控制的数据集，以此来进行模型参数训练。

无功优化的目标函数如式（12）所示，其包含有功网损和节点电压越限惩罚项，有功网损为系统最优时配电网各支路损耗之和，节点电压越限惩罚能够保证配电网运行时节点电压在合格范围内。

式中：rij为支路ij的电阻值；Iij(t)为t时刻支路ij的电流；M为配网线路集合；Ui、Uimax、Uimin分别为节点i的电压幅值及其上下限值；λ为节点电压越界的惩罚因子；Uilim为节点i电压越限时的设定值；NPQ为配电网中的PQ节点集合。

同时，无功优化模型包含系统运行的各类约束条件，主要有等式约束和不等式约束。

1）潮流等式约束。

式中：Pi和Qi分别为节点i注入的有功功率和无功功率；Gij和Bij分别为节点i和j之间的电导和电纳；θ为节点i和j之间的电压相位差。

2）电网运行参数不等式约束。

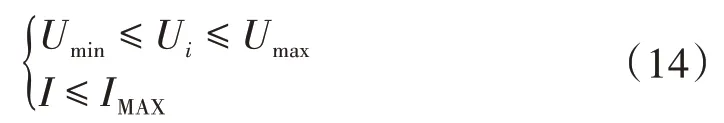
式中：IMAX为支路通过的最大电流值；Umin和Umax分别为节点i电压所允许的上下限。

3）无功设备控制不等式约束。

式中：QDG.i.min和QDG.i.max分别为节点i上连接的DG 无功出力的上下限；Qsvc.i.min和Qsvc.i.max为节点i上连接的静止无功补偿器出力上下限；Tmin和Tmax分别为有载调压变压器分接头的最低档和最高档位；Cmin和Cmax分别为节点i处电容器投切组数。

2.2 基于OS-ELM的配电网无功优化模型

从函数的非线性映射的角度分析，数据驱动无功优化关键在于构建配电网的运行状态和无功配置策略之间的映射关系。通过OS-ELM 对系统状态和无功策略之间的关系进行理解学习，对于系统的实时运行状态，将特征数据作为网络的输入，最终通过已经训练好得网络得出对应状态的无功补偿策略。配电网的运行特征数据较多，通过潮流计算能判定某些特征数据之间存在的联系。数据驱动无功优化的模型如图3所示，可表示为

图3 配电网无功优化模型

式中：g(·)为网络模型；S为P、U对应场景下的无功优化策略。

无功优化模型的核心是通过构建的数据集进行网络的训练，无功优化框架主要包含以下步骤：

1）数据的提取和预处理。确定电网的拓扑结构，提取各节点的历史负荷、分布式能源发电及相应的电网设备参数，构建配电网运行数据库。

2）基于配电网运行数据库，使用优化算法对配电网历史运行场景进行无功优化计算，得到对应的无功优化策略，构建OS-ELM 无功优化策略样本库。

3）训练OS-ELM。将样本数据分为训练集和测试集，训练集用来确定OS-ELM 的网络参数，测试集用来评估OS-ELM 的性能。考虑到输入数据差异过大，容易造成网络精度降低，采用离差标准化法将输入的特征数据映射到区间［0，1］中

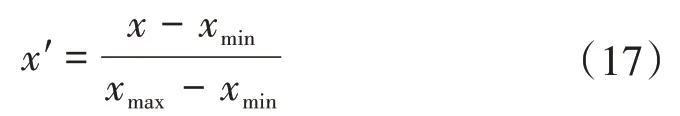
式中：x为归一化前的变量；x′为归一化后的变量；xmax为变量的最大值；xmin为变量的最小值。

归一化后选取合适的激活函数，根据样本的输入和输出训练网络，通过预测值和实际值之间的误差来修正网络的参数。经过数据迭代最终确定OS-ELM 的输出层权重，得到在线无功优化模型。

4）在线应用阶段。当电网实时数据到来时可以提取电网的特征数据，利用训练好的OS-ELM模型直接得出对应的无功优化策略。

3 算例分析

3.1 算例设置

为了验证本文方法的有效性和合理性，以IEEE 33 节点系统为仿真系统进行验证，系统如图4 所示。节点0 是平衡节点，光伏出力结合山东某光伏电站的实际数据进行概率密度分析，得到对应的beta 分布形状参数为a=0.686 9，b=2.132 0；风电服从双参数威布尔分布，风电的有功出力的形状参数为k=1.637，c=5.218；SVC 的容量为300 kVA，分别安装在14、30 号节点位置；电容器容量为200 kVA，分组投切，最多投放四组，安装在6 号节点位置；变压器变比范围0.9～1.1，分级步长为0.012 5。

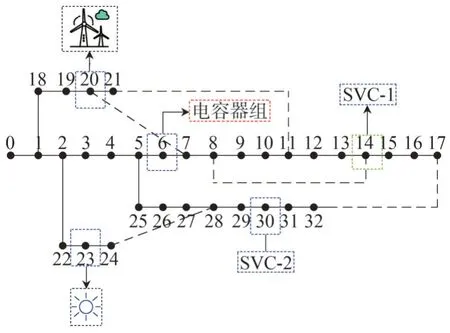
图4 IEEE 33节点算例

3.2 数据集的构建

基于OS-ELM 的配电网优化模型的关键之一就是数据集的构建。通过分析影响无功功率、负荷、和电压分布的数据源，将负荷功率、光伏发电出力、风力发电出力3 种数据集构成无功优化的输入特征集，神经网络的输入集为35 维；通过改进粒子群算法计算每种场景下的无功优化策略，以此作为神经网络的输出集，由此构造数据集进行训练。本文结合某地配电网1 年内的负荷变化规律，根据蒙特卡洛算法进行均匀抽样，得出配电网运行场景采用改进粒子群算法对每一个运行场景进行优化，得出对应的无功最佳策略。表1 给出了4 种运行场景的具体情况。

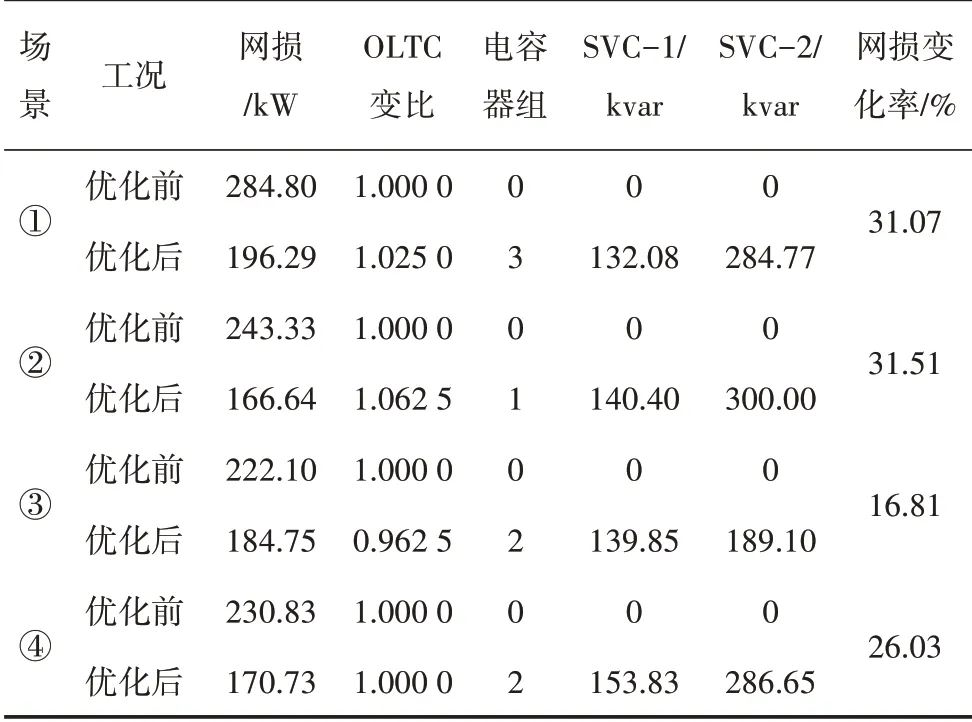
表1 4种随机场景下优化前后对比

由表1 可知构造无功优化策略集的算法具有较好的优化效果，在4 种随机场景下有功网损分别下降31.07%、31.51%、16.81%、26.03%。针对4 种运行场景，加入无功补偿装置前后电压的变化如图5 所示，4 种场景下系统电压较优化前合格率提升较好。

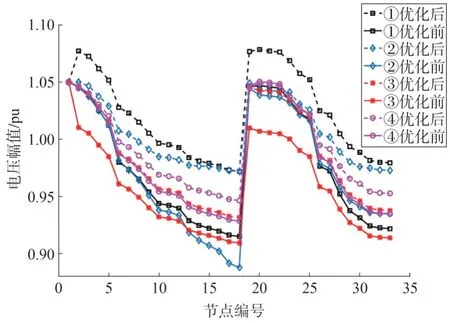
图5 4种场景下优化前后电压变化

3.3 OS-ELM的训练

为了验证在线无功优化的准确性和合理性，将测试1 080 组数据中的960 组为作为训练数据，120组作为测试数据，以此来验证在线无功优化的准确性。图6 给出了OS-ELM 测试对比，均方误差和拟合优度的对比如表2 所示。由图6 可知数据驱动方法能够准确地描述配电网运行参数与无功优化策略间的对应关系，控制变量的参数变动和实际无功优化结果几乎一致。不同运行场景运行下各控制变量的对比误差如表3所示。

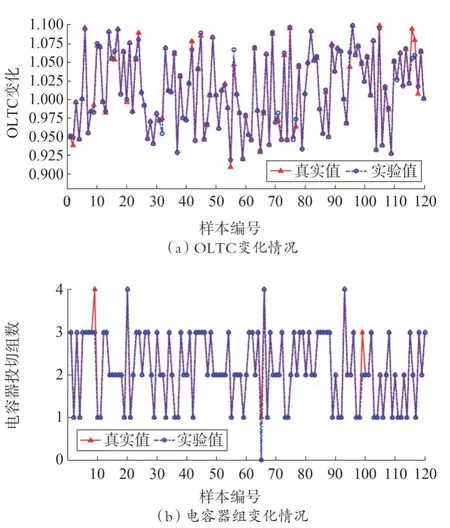
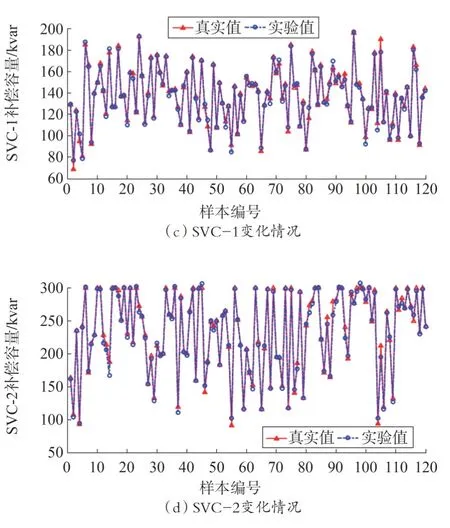
图6 测试集数据优化效果对比

表2 测试集误差

3.4 无功优化效果对比

为验证所提方法的优化效果，基于粒子群算法构建模型训练基准数据，利用本文算法分别和BP神经网络、支持向量机和径向基函数神经网络构建无功优化模型，并以网络损耗Closs和电压总偏差Uloss为参考值进行优化结果对比分析。利用蒙特卡洛方法选取电网运行的24 种场景，利用上述方法分别构建无功优化模型进行对比，计算在不同方法下的网络损耗率Closs和电压总偏差率Uloss，如式（18）和式（19）所示，结果对比图7 和图8 所示。

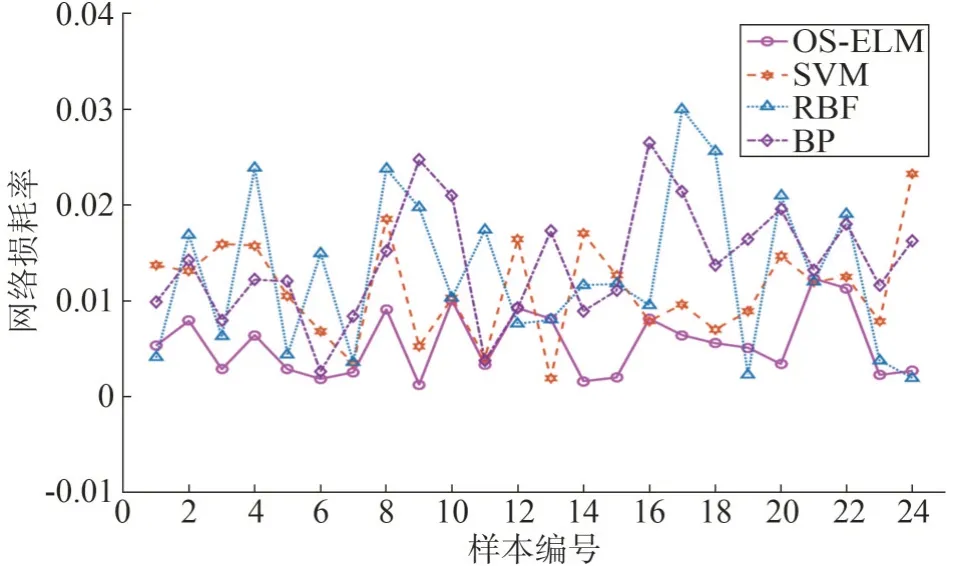
图7 不同算法对应的网络损耗率

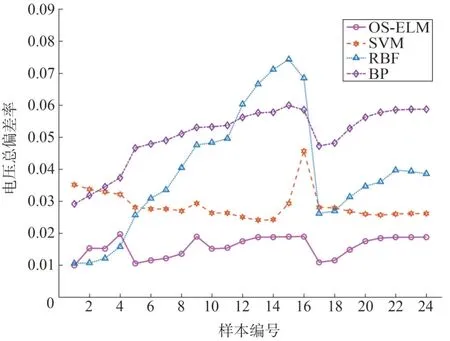
图8 不同算法对应的电压总偏差率

式中：CT、UT分别为本文所提方法或对比方法对应的网络损耗、电压总偏移量；CP、UP分别为基准的网络损耗和总电压偏差量。

从图7和图8可以看出，相对于径向基函数神经网络等构建的无功优化模型，本文方法在网络损耗率和电压偏差率两方面具有明显的优势，其平均误差分别为0.55%和1.58%，不同方法间网络损耗和电压偏差平均值对比如表3 所示。上述实验表明OSELM 模型的优化结果是合理和有效的，且表现出良好的学习和理解能力。

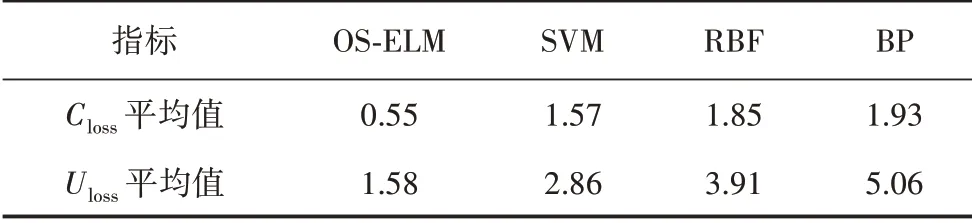
表3 Closs和Uloss的平均值 单位：%

在线无功优化的关键是计算速度和性能的稳定，对于传统方法和神经网络方法在无功优化计算的耗时进行分析，其中OS-ELM 耗时0.028 s，SVM 耗时0.052 s，RBF 耗时0.082 s，BP 耗时0.125 s。传统方法计算速度主要受制于潮流计算和启发式算法的寻优过程，对于机器学习方法，主要分为两个阶段，第一阶段是离线训练阶段，第二阶段在线应用，因此在线应用时由于其基于离线的训练，因此优化时间较短。

进一步分析本文方法作用下无功控制策略控制变量的变化情况，同样以粒子群优化结果为基准进行比较，不同场景下控制参数的误差以及平均误差如表4所示，图9给出了不同场景下不用方法的控制变量误差对比。由表4 个可以看出，本文提出的基于OS-ELM 无功优化方法对于控制变量的调整最接近于最优状态，其误差的平均值最小。

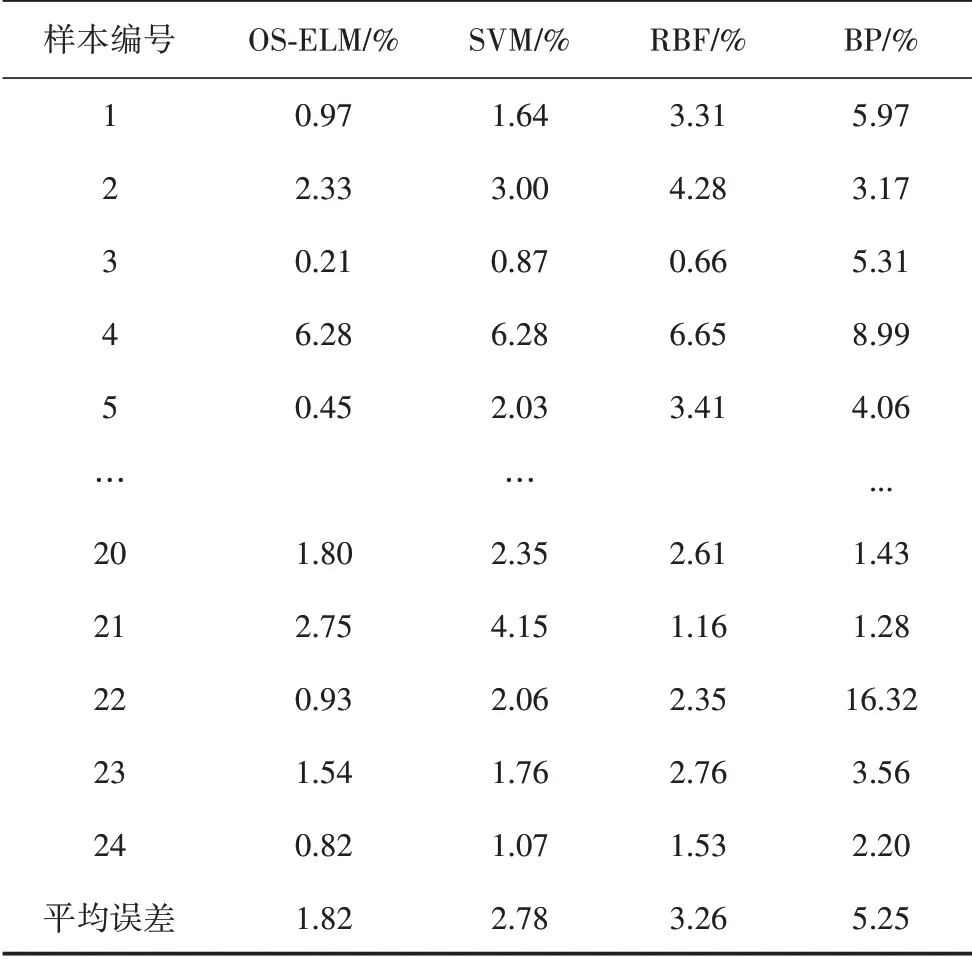
表4 不同优化方法的SVC-1的平均相对误差

图9 不同算法结果的相对误差

4 结语

随着大量柔性可控资源的接入其运行和控制无法准确预测，由此给配电网的无功电压控制带来困难。提出一种基于数据驱动的配电网无功电压优化方法，利用在线极限学习机的非线性映射能力描述配电网系统运行状态与无功设备控制策略间的映射关系。在无需指导配电网网络架构以及无功优化物理建模的基础上，充分利用配电网历史运行数据，实现配电网的无功优化，提高系统电压无功控制能力以及无功电压的主动控制能力。最后，通过仿真算法验证了本文方法的有效性和准确性，利用数据驱动方法能够实现无功电压控制的精细化管理。