双幅变孔径筛面物料抛掷运动机理与优化

宋宝成，江海深，田祖织

1江苏安全技术职业学院 江苏徐州 221000

2中国矿业大学化工学院 江苏徐州 221116

3国家煤加工与洁净化工程技术研究中心 江苏徐州 221116

4中国矿业大学机电工程学院 江苏徐州 221116

振动筛是重要的矿物加工装备，广泛应用于各类选矿作业[1-2]。振动筛分工艺过程大多基于物料抛掷运动理论，采用抛掷指数衡量筛面上物料实现抛掷运动的能力[3]。Xiao J Z 等人[4]建立了一种具有摆动轨迹振动筛的抛掷指数分布函数，分析了颗粒落点位置的影响，认为抛掷指数是决定筛分效率的直接因素。Yin Z J 等人[5]在推导椭圆筛抛掷指数的基础上分析了抛掷指数与物料运动速度的关系，认为合理的抛掷指数有助于物料输送过程中的松散分层。刘德洋等人[6]推导了采用附加气室空气弹簧隔振的振动筛抛掷指数，通过改变振动频率与振幅实现了抛掷指数的调节。

双幅变孔径筛面采用刚柔耦合的方式，兼顾刚性筛面与柔性材料筛面的优点。振动过程中，相邻筛杆具有不同的振幅，可以获得筛孔孔径的周期性变化，对典型的堵孔现象能够实现有效预防[7]。然而双幅变孔径筛面的几何结构与振动方式较为复杂，传统筛面的物料抛掷机理对其不再适用。为此，本文在建立双幅变孔径筛面颗粒受力模型的基础上，得到了其抛掷指数分布函数；对其筛分过程进行了数值模拟，以筛分效率为指标，分别采用 GA、LRGA 与 GRNN 神经网络结合的方法对抛掷指数各因素进行优化，以得到理想的抛掷指数分布，为相关产品的设计研发提供参考。

1 物料抛掷机理分析

双幅变孔径筛面结构如图 1 所示。普通筛杆与筛框固连，与增强筛杆交替布置。增强筛杆末端通过橡胶块与筛框柔性连结。在约束槽作用下，在x方向，增强筛杆振幅A2x与普通筛杆振幅A1x相同。

图1 筛面结构与孔径变化Fig.1 Structure of screen surface and variation of aperture

当筛杆质量m、橡胶块刚度k与激振频率ω满足时[7]，在y方向，增强筛杆与普通筛杆振动同相，且振幅A2y＞A1y，孔径dt产生周期性变化：

式中：b0为相邻筛杆中心间距；r为筛杆半径。

如图 2 所示，以颗粒质心为局部坐标系O xpyp原点，yp为接触点法向，xp为接触点切向。全局坐标y指向竖直方向，x由入料端指向出料端。令普通筛杆与增强筛杆振动方向角分别为α1与α2，当xp与x的夹角与αi(i=1，2) 一致时 (如图 2(a) 中xp')，筛杆对颗粒的支撑力N与振动方向垂直，筛面振动将无法得到N为 0 的平衡条件[8]，此处为颗粒被筛面振动作用抛起的左极限位置。当xp与重力方向一致时 (如图 2(a) 中xp″)，筛杆对颗粒的支撑力N始终为 0，筛面振动对颗粒将不再产生作用，此处为颗粒被筛面振动作用抛起的右极限位置。将yp与y的夹角δ i称为颗粒筛杆间的接触偏角，所以抛掷指数存在的条件为δi∈(0，αi+0.5π)，其中i=1，2。

图2 双幅变孔径筛面颗粒受力模型Fig.2 Force model of particle on double-amplitude variable-aperture screen

对满足δi∈(0，αi+0.5π)(i=1，2) 的颗粒，颗粒受力情况如图 2(b) 所示。分别建立xp与yp方向平衡方程为

式中：Ai为筛杆振幅。

令抛始角为φsi，由颗粒抛掷运动临界条件N=0[8]可得

由此可知，振动强度Asi与抛掷指数AVi分别为

可见，由于A2x=A1x且A2y＞A1y，所以增强筛杆具有更大的振动强度 (Ks2＞Ks1)，且Ks1与Ks2均为定值，不随颗粒与筛杆接触位置的改变而改变。而抛掷指数与颗粒、筛杆间的接触位置有关，在 (0，α i+0.5π) 范围内，随δi单调递减。将δi=90°时的抛掷指数称为顶点抛掷指数，由式 (6) 可知，使得相同δi条件下KV2＞KV1。

由于A2x=A1x，A2y＞A2y，所以，即增强筛杆的有效抛掷范围大于普通筛杆。分别对α i、Ksi求偏导，由于Ksi大于 1[10]，可得

因此，对于普通筛杆与增强筛杆，振动方向角αi与振动强度Ksi越大，那么筛杆能够使颗粒抛离筛面的有效抛掷范围越大。

2 筛分数值模拟与参数优化

2.1 筛分数值模拟

图3 所示为 EDEM 环境下双幅变孔径筛面离散元数值模拟模型。考虑到筛面宽度主要影响处理量，对筛分效率影响甚微，故筛面模型采用大长宽比参数 (1 010 mm×90 mm) 以提高数值模拟效率[11]。初始孔径d=10 mm。利用颗粒填充技术模拟实际物料的复杂外形，以 0.6 kg/s 速率持续给料 (粒度小于d与大于d的物料比为 2∶3)，模拟单位面积处理量为 23.76 t/(h·m2) 的筛分过程；采用网格单元组 (Grid Bin Group) 获取筛下物与筛上物的动态成分，直至获得稳定的筛分效率η。物料密度为 1 300 kg/m3，筛杆密度为 7 800 kg/m3，其他物性参数如表 1 所列。

图3 双幅变孔径筛面离散元数值模拟Fig.3 Discrete element numerical simulation on doubleamplitude variable-aperture screen

表1 筛分数值模拟参数Tab.1 Parameters of screening numerical simulation

由式 (5)、(6) 可知，当激振频率固定时，影响双幅变孔径筛面物料抛掷效果的因素包括Aix与Aiy。在A1y与A2y协同作用下孔径发生变化，为了便于分析该协同关系对筛分效果的影响，引入孔径最大变化率ξ。由式 (1) 可知

取r=5 mm，b0=20 mm，进而可将筛分效果影响因素简化为筛杆水平方向振幅 (因素A)、普通筛杆竖直方向振幅 (因素B) 及孔径最大变化率 (因素C)。取振动频率为 16.67 Hz，因素A、B分别具有 2.5、3.0、3.5、4.0、4.5 这 5 个水平值，因素C的 5 个水平值依次为 0.5、1.0、1.5、2.0、2.5。表 2 所列为相应正交试验 (序号 1～25) 及补充因素水平组合 (序号 26～31) 数值模拟所得结果。

表2 数值模拟结果Tab.2 Numerical simulation results

表3 所列为极差分析结果，因素A、B、C在相应的水平值范围内对指标η的影响显著性由大到小依次为C、A、B，孔径最大变化率对筛分效率影响最大。最佳因素水平组合为A3-B4-C4，该条件下 (序号 26) 的数值模拟结果为 92.724%，高于其他条件所得指标，证明了极差分析结果的可靠性。同时可以发现，指标η随因素A、B、C均呈现先增大后减小的趋势，适中的孔径最大变化率有利于提高筛分效率。

表3 极差分析结果Tab.3 Range analysis results

2.2 抛掷指数参数优化

取因素A、B、C为网络输入，指标η为网络输出，对数值模拟结果进行归一化处理后，以序号 1～26 数据为训练样本，以序号 27～31 数据为检验样本，采用 GRNN 神经网络进行数据拟合，流程如图 4 所示。分别采用 GA 与 LRGA[12]对 spread 进行优化，并对所得优化的 GRNN 神经网络进行参数寻优，以得到指标η最大值对应的因素A、B、C值。

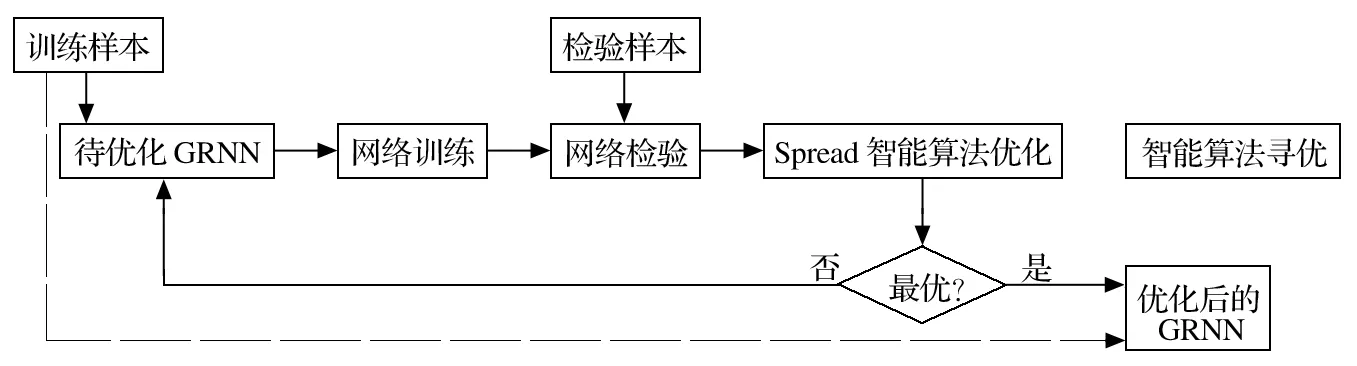
图4 拟合与寻优流程Fig.4 Process flow of fitness and optimization

图5 所示为分别采用相同算法参数 (种群规模，30；交叉概率，0.9；变异概率，0.01；进化代数，30) 的 GA 与 LRGA 进行 10 次拟合寻优所得结果。可以发现，采用 GA 所得结果较为离散，不能满足优化需要；采用 LRGA 所得结果更为稳定，可信度更高。对 LRGA 所得寻优结果进行反归一化处理，并以此参数进行数值模拟验证，得到筛杆水平方向振幅Aix为 3.78 mm、普通筛杆竖直方向振幅A1y为 3.92 mm、孔径最大变化率ξ为 2.1% 时，筛分效率为 93.576%，高于极差分析所得最佳结果。

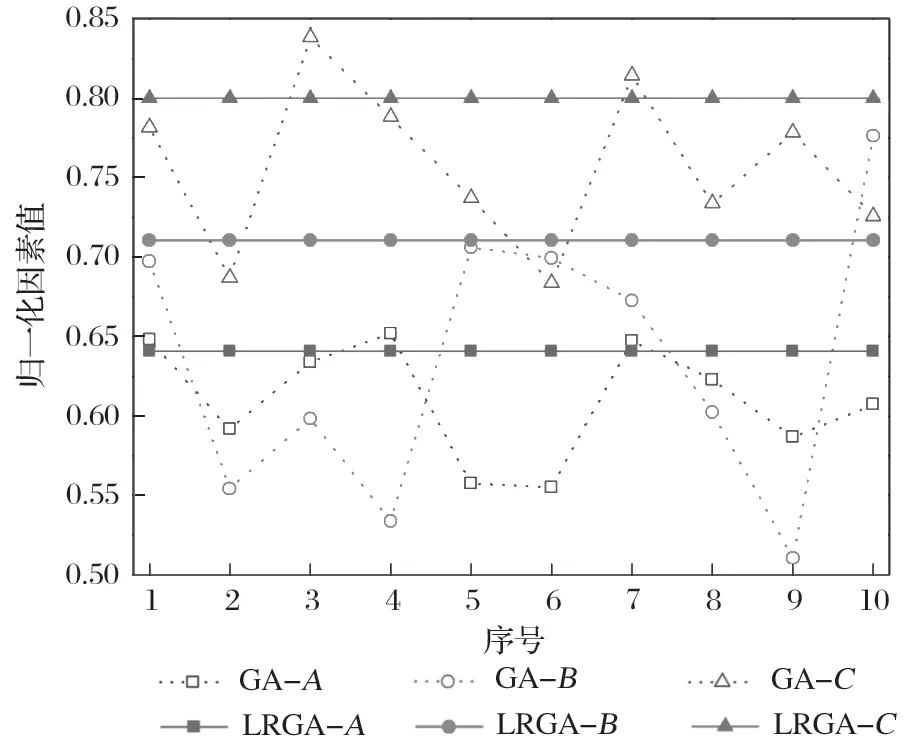
图5 寻优结果Fig.5 Optimization results

由式 (10) 可知，此时增强筛杆竖直方向振幅A2y为 6.83 mm，进而计算可得：普通筛杆振幅A1=5.45 mm，振动方向角α1=46.04°，增强筛杆振幅A2=7.81 mm，振动方向角α2=61.04°，普通筛杆、增强筛杆抛掷指数存在条件分别为δ1∈ (0，136.04°)，δ2∈(0，151.04°)。代入式 (5)、(6) 可得振动强度Ks1=6.089，Ks2=8.725，并得到筛杆抛掷指数分布优化结果：

图6 抛掷指数分布曲线Fig.6 Throwing index distribution curve

3 结论

(1) 普通筛杆与增强筛杆的振动强度均为定值，且增强筛杆振动强度较大。当颗粒筛杆间的接触偏角δi∈(0，αi+0.5π) 时，抛掷指数存在，其值随δi单调递减。

(2) 双幅变孔径筛面筛杆有效抛掷范围与振动方向角α i、振动强度Ksi正相关，增强筛杆的有效抛掷范围大于普通筛杆。

(3) 抛掷强度的影响因素中，ξ对筛分效果影响最为显著。当Aix=3.78 mm、A1y=3.92 mm、ξ=2.1% 时，可以获得最高的筛分效率为 93.576%。

(4) 最佳抛掷指数分布条件下，普通筛杆与增强筛杆的顶点抛掷指数分别为 4.38 与 7.63，有效抛掷范围分别为 (0，128.69°) 与 (0，147.52°)。