基于一种两侧独立驱动全驱轮式底盘的转向性能分析

张明松 ，胡亚朋

（三峡大学机械与动力学院，湖北 宜昌 443002）

随着科技的不断进步，人们不断研究各种大型机械辅助完成公路、桥梁、建筑、地下工程、抢险等重大工程项目。改革开放以来，我国在基础设施建设方面的投资不断加大，在这些基础设施建设中往往需要特种机械车辆的辅助。这为工程机械车辆技术研发的突破提供了有利条件。本文所研究的两侧独立驱动全驱轮式底盘采用两侧电机独立驱动模式，接下来将对底盘的合理性进行研究。

1 底盘转向运动学分析

差速率即两侧独立驱动全驱轮式底盘的两侧车轮的差速程度。当底盘转向时，差速率e计算公式[1]为：

两侧独立驱动全驱轮式底盘转向过程中，前后轴应该有同一个转向中心，并且绕着各自的圆周作纯滚动。假设在某时刻，底盘以瞬时转向半径R1绕瞬时圆心点O转向，其车速及半径关系[2]为：

式中，B为两侧车轮的中心距离，单位为m；ΔV为两侧驱动轮轮速之差，单位为m/s；V1为左侧瞬时轮速，单位为m/s；V2为右侧瞬时轮速，单位为m/s。

2 底盘转向动力学分析

二自由度动力学模型：两侧独立驱动全驱轮式底盘在行驶过程中，横摆运动与侧向运动相互影响，故二自由度动力学模型更符合两侧独立驱动全驱轮式底盘的实际运动情况[3]。考虑到本研究的研究模型没有转向机构，故不考虑前轮转向角的影响，根据经典力学理论及轮胎受力情况[4]，建立二自由度转向动力学模型，如图1所示。

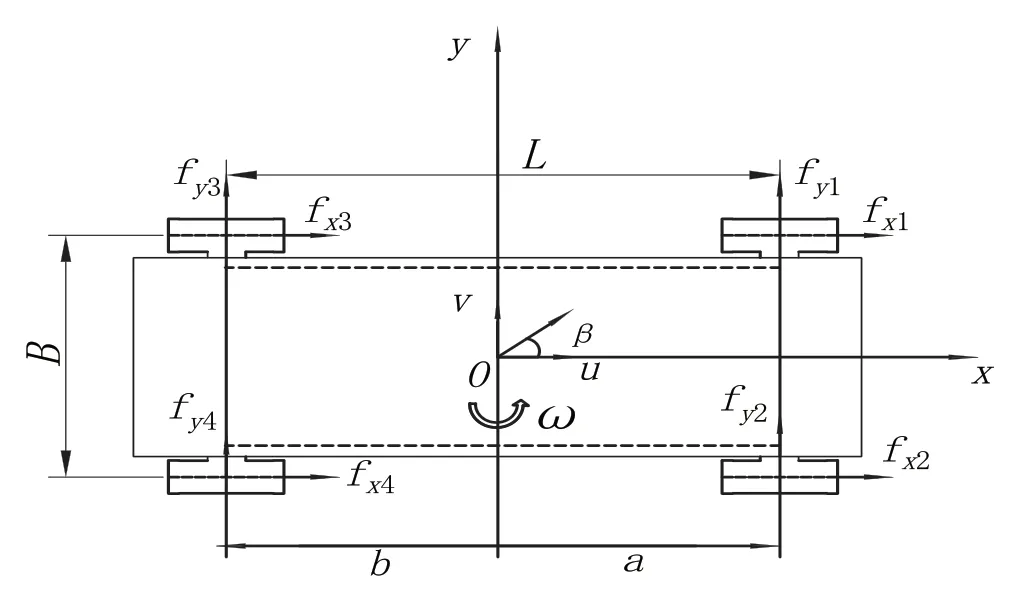
图1 二自由度转向动力学模型

侧向运动微分方程为：

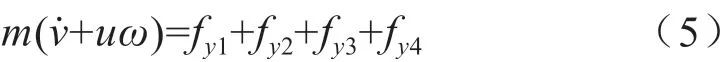
横摆运动微分方程为：

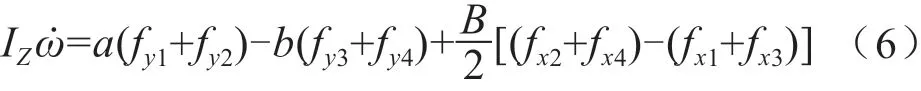
其中，m为整车质量，a和b分别为前后轴到质心的距离，L为前后轴之间的距离，IZ为整车绕Z轴的转动惯量，u和v分别为车辆的纵向和侧向速度，ω为车辆的横摆角速度，fxi为轮胎受到的纵向力，fyi为轮胎受到的侧向力，i=1，2，3，4。

底盘在进行转向时，主要受到两种形式的转向阻力，即地面变形阻力和转向阻力矩[5]。计算地面变形阻力的方法可参照直线行驶时地面变形阻力的计算方法，设内外车轮受到的地面变形阻力分别为f1和f2。则f1=f2=0.5f G。

在转向过程中，由于内外侧车轮的转速不同，地面对轮胎产生的摩擦力也不同[6]。轮胎将受到更大的阻力，所以需要取内外侧电机功率差更大的值，而不同的转向半径需要电机输出的功率及底盘消耗的功率也不相同。研究转向半径与功率差值之间的关系，可对转向系统的性能进行优化并为转向过程控制提供理论依据。接下来对两种情况下底盘转向时轮胎的受力情况进行分析。

2.1 原地中心转向

原地中心转向时，两侧电机处于驱动状态。两侧电机工作状态为：输出的转矩和转速大小相等，方向相反。此时转向半径在0~B/2之间。实现该类转向的机械传动系统是十分复杂的，而且系统本身控制比较复杂[7]。采用电机驱动可灵活实现正反转并精确控制电机转速及转矩，实现底盘自身灵活运动。底盘转向时轮胎的受力情况如图2所示。

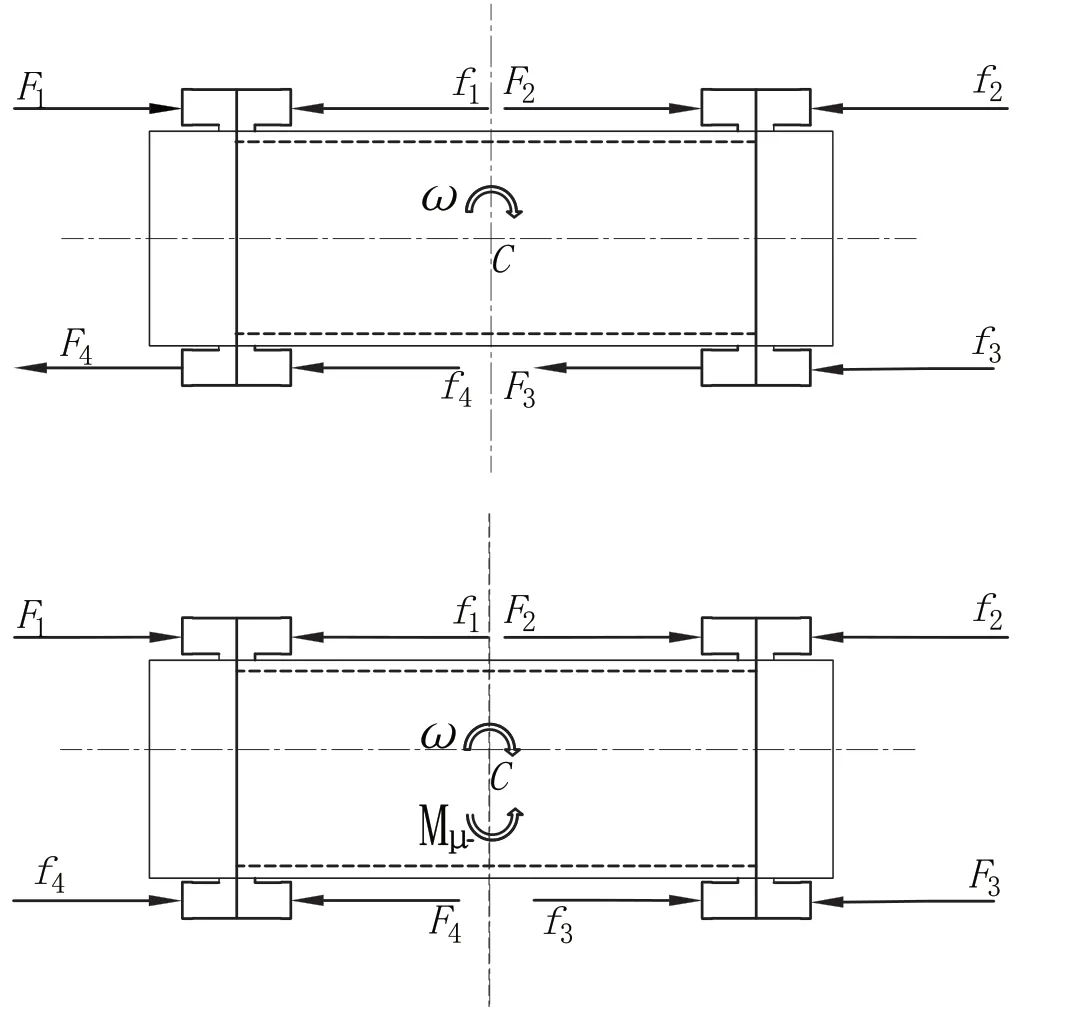
图2 底盘转向时轮胎的受力分析

根据匀速转向的条件可推出：

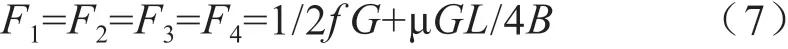
此时内外侧车轮受到的驱动力的大小相等，当转向半径R=0时，车轮受到的转向阻力矩最大，此时内外侧电机输出的扭矩相对其他转向过程电机输出的扭矩更大。中心转向可以减少底盘转向时的占地面积，使底盘转向更加灵活。

2.2 车身外一点转向

当底盘以车身外一点转向时，轮胎的受力分析如图3所示。外侧电机输出电动转矩，内侧电机工作在发电机状态，产生制动转矩[8]。相应的外侧车轮受到驱动力F1和F2，由于前后轮之间用链传动连接，故前后轮受到的驱动力大小相等。内侧受到制动力F3和F4，同理F3=F4。根据底盘匀速转向的条件，可以得到：

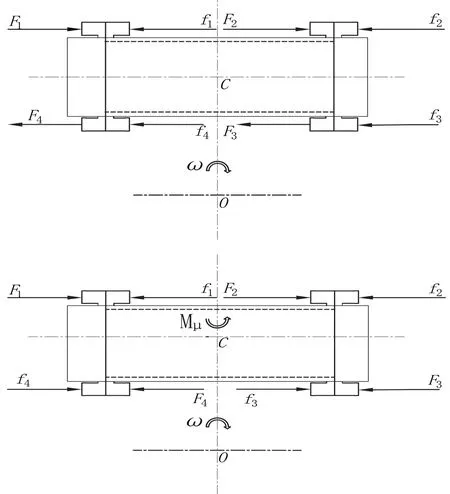
图3 底盘以车身外一点转向时轮胎的受力分析

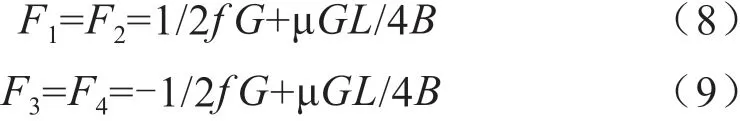
3 建立底盘模型

在现在产品的研发过程中，通常先利用计算机仿真软件对汽车的整体和零部件进行建模仿真，这使得在研发的初期阶段能够及时发现设计中存在的问题，修改零部件参数并调整控制策略。因此，接下来本文将利用计算机仿真技术对双侧电驱动车辆的整车转向动力学性能进行建模和仿真[9]。

3.1 底盘参数

通过上文对底盘进行动力学及运动学理论分析后，得到其运动方程，基于理论公式，通过Carsim软件搭建底盘仿真模型，具体的结构参数如表1所示。

表1 底盘结构参数

3.2 Carsim建模

通过Carsim交互式仿真平台，对底盘结构参数进行设置，具体情况如图4所示。设置道路工况为双移线，如图5所示。

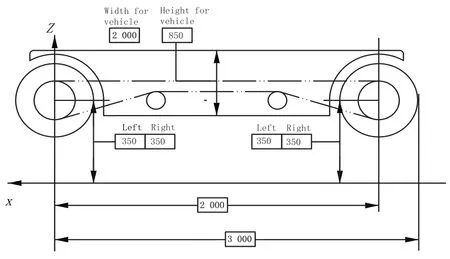
图4 底盘结构参数

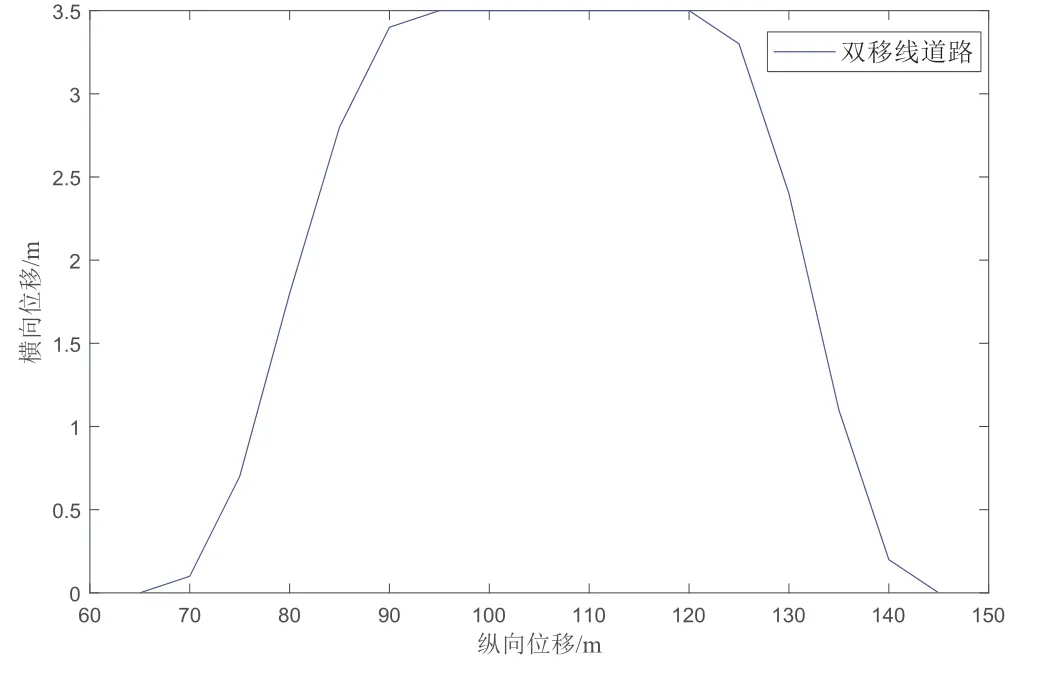
图5 双移线道路

4 仿真分析

为了分析前面所建立的底盘模型的操纵稳定性能，根据国家标准对模型进行双移线试验以及转弯半径试验，并进行模拟仿真，根据仿真结果对整车操纵稳定性进行评价[10]。结合所设计的车辆参数，确定本车的试验车速为10 km/h、25 km/h、40 km/h，试验道路附着系数为0.85，对本车进行双移线试验。

4.1 横摆角速度

通过双移线仿真试验测得车辆在10 km/h、25 km/h、40 km/h的车速下行驶时的横摆角速度对比情况，如图6所示。由图6可知车速为10 km/h时，底盘在转弯时的横摆角速度最大值为20 rad/s，此时底盘的侧向加速度为0.25 g。车速为25 km/h时，底盘通过双移线时的最大横摆角速度为32 rad/s，此时底盘的侧向加速度最大值为0.43 g。当底盘以40 km/h行驶时，底盘通过双移线时的最大横摆角速度为38 rad/s，此时底盘的侧向加速度为0.8 g，超出预设范围，底盘的稳定性变差，会导致车轮侧滑，最终造成侧翻。因此可以得出，该底盘最高车速在小于25 km/h时，其操纵稳定性能可控制在较理想的范围内。

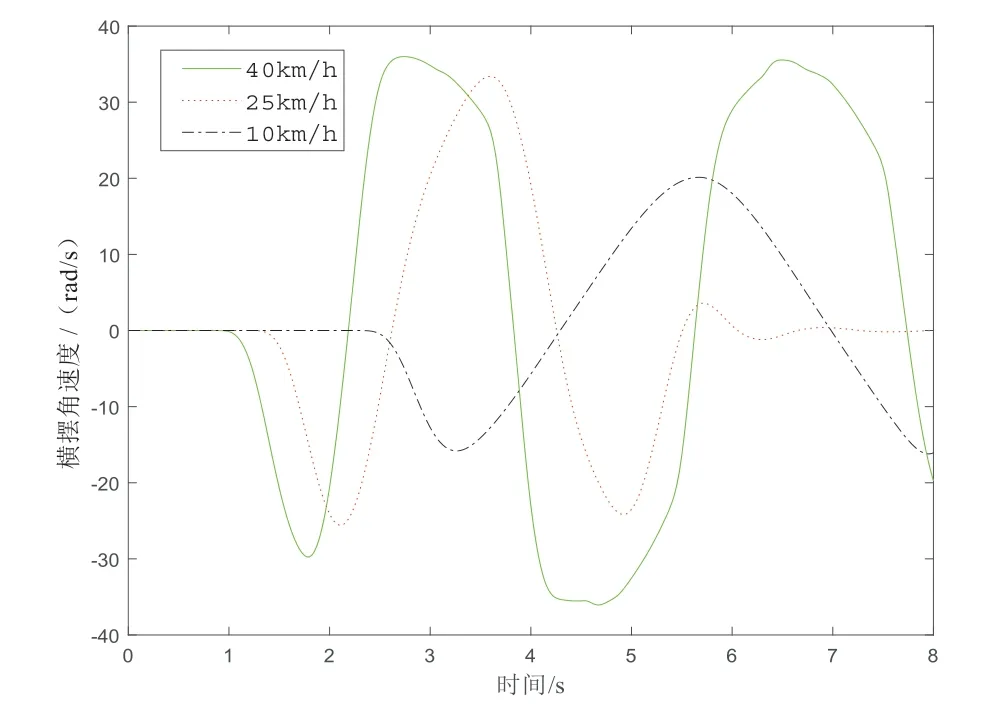
图6 横摆角速度对比图

4.2 转弯半径

最小转弯半径试验，即当底盘两侧车轮按照一定差速率行驶时，随着车速增加，在保证底盘不发生侧滑的前提下，所能通过的最小转弯半径。最小转弯半径越小，底盘行驶时的机动性能越好。车辆由开始加速至最大稳定车速25 km/h时，车辆通过的转弯半径及侧向加速度对比如图7、图8所示。

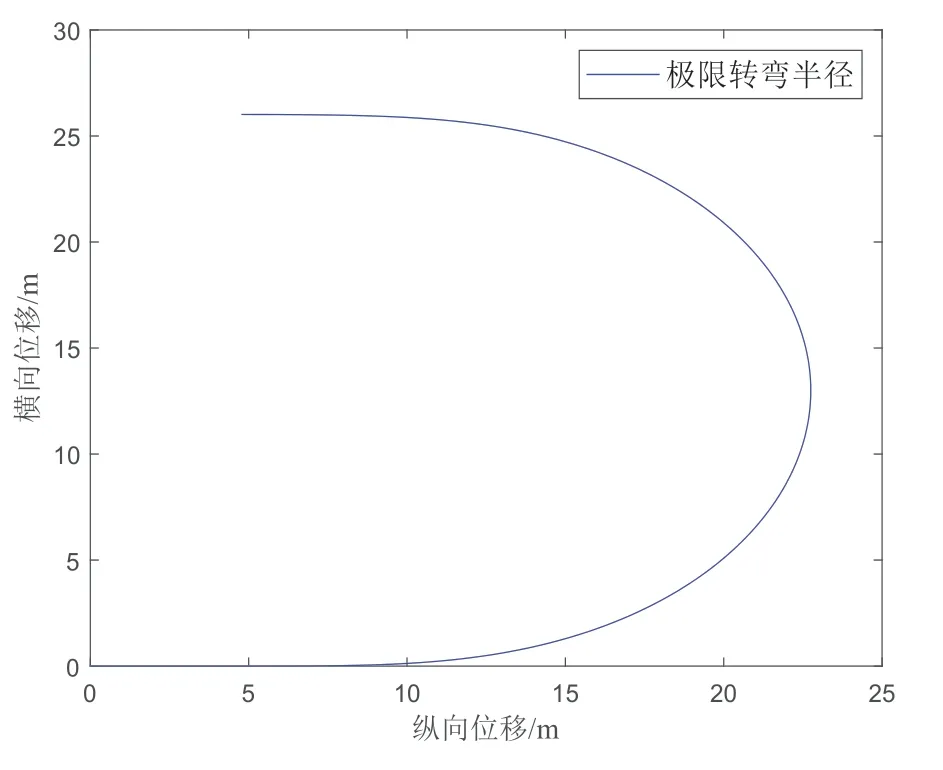
图7 转弯半径

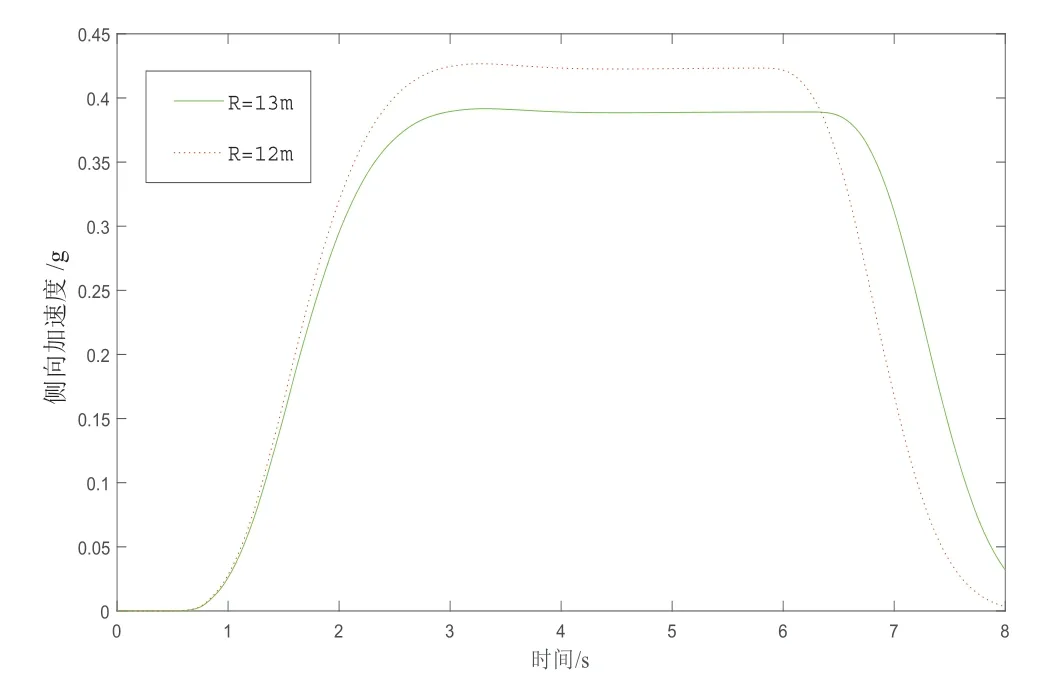
图8 侧向加速度对比

由图8可知，当底盘的转弯半径R＞13 m时，底盘通过此半径的侧向加速度小于0.4 g，当底盘的转弯半径R＜13 m时，侧向加速度大于0.4 g，此时轮胎与地面将产生滑移，因而根据工程车辆底盘设计要求，此底盘的最小转弯半径不应小于13 m。

5 结论

本文以二自由度两侧独立驱动全驱轮式底盘为研究对象，建立了底盘的动力学及运动学理论模型，并对底盘的参数进行设计，通过Carsim仿真软件对底盘的合理性进行验证。分析得到以下结论：

1）底盘的行驶稳定性受速度、质心高度、转弯半径等因素影响，其中速度和转弯半径变化对底盘的稳定性影响较大。当底盘速度大于设定值25 km/h时，底盘在双移线试验中的侧向加速度大于0.4 g，底盘的稳定性变差。

2）当转弯半径R＜13 m时，轮胎与地面将产生滑移，导致底盘侧滑。故该底盘的最高车速不应超过25 km/h，以最高车速行驶时，转弯半径不应小于

13 m。