基于一类新的直觉模糊熵的供应商选择决策法

刘婉贞

(长沙职业技术学院基础课教学部，湖南 长沙 410217)

0 引言

随着模糊集在各个领域的成功应用，很多新的拓展的模糊集相继被提出，如直觉模糊集、犹豫模糊集、图像模糊集和q阶模糊集等[1-4]。直觉模糊集通过引入非隶属度参数，可以考察决策者对待事物进行评价的3个方面：支持、反对和中立，克服了扎德教授所提出的经典的模糊集只能给出是与否两方面的不足。直觉模糊集的概念最早由Atanassov[5]提出，后经众多学者的研究，现已经成为决策领域中一个重要的研究内容，并且被成功应用到诸如经济管理、图像分割、医疗诊断等领域[6-8]。

熵是信息论中重要的概念，可以度量数据信息的不确定程度。近年来，熵的概念被引入到模糊决策中，例如熵权法是一种非常出名的属性权重确定方法。自从Burillo等[9]将熵的概念引入到直觉模糊集并提出直觉模糊熵的概念以来，吸引了很多学者致力于直觉模糊熵的构造以及基于熵的多属性决策法的研究与应用。如Verma等[10]构造了一类基于指数函数的直觉模糊熵公式，并发展了基于熵的决策方法；魏翠萍等[11]构造了基于三角函数的直觉模糊熵公式，并通过比较分析描述了熵的有效性。还有更多的学者对直觉模糊熵进行了相关研究[12-13]。

饲料行业是一个关系国计民生的重要行业，处在整个行业供应链的中间，既影响种植业，也影响养殖业。最近几年，饲料行业面临产能过剩、产品同质化严重和原材料成本越来越高的处境，要保持行业的竞争力，饲料企业需要更加重视在供应链管理理念下的供应商选择问题，以达到降本增效的目的。

饲料企业供应商评选包含多个难以量化的定性指标，是一个模糊多属性决策问题。直觉模糊集可以较好地刻画定性属性，为此，本文研究基于直觉模糊信息的饲料供应商选择问题。本文将首先构造一类新的直觉模糊熵，然后发展基于熵的属性权重确定方法，最后提出基于新的熵的直觉模糊多属性决策方法，并通过饲料供应商选择算例说明决策方法的有效性和可行性。

1 直觉模糊熵概述

首先回顾一些直觉模糊的基本概念、运算法则等[5，9]，然后给出新的直觉模糊熵的计算公式。

定义1:设T为一给定的集合，则定义在T上的一个直觉模糊集A具有如下表示形式：

A={|ti∈T}

式中:uA:Ta[0，1]和vA:Ta[0，1]分别为A的隶属度(满意度)和非隶属度(不满意度)函数，且它们满足如下性质：对任意的t∈T，有0≤uA(tj)+vA(tj)≤1成立。特别的，当T中只有一个元素，则A简记为，并被称为直觉模糊数或直觉模糊值。

定义2:设A={|ti∈T}和B={|ti∈T}，为2个任意的直觉模糊集，则直觉模糊集的运算法则定义为：

①A⊆B⟺uA(ti)≤uB(ti)，vA(ti)≥vB(xi)，∀ti∈T；

②A=B⟺A⊆B和B⊆A；

③AC={|ti∈T}。

定义3:称映射E:IFS(X)→[0，1]为直觉模糊熵，若其满足如下条件：

(C1)E(A)=0当且仅当A为分明集；

(C2)E(A)=1当且仅当uA(ti)=vA(ti)，∀ti∈T；

(C3)E(A)=E(AC)；

(C4)对于∀xi∈X，若(i)当uB(ti)≤vB(ti)，且uA(ti)≤uB(ti)，vA(ti)≥vB(ti)时；

或者(ii)当uB(ti)≥vB(ti)且uA(ti)≥uB(ti)，vA(ti)≤vB(ti)时；都有E(A)≤E(B)。

下面将构造一个新的直觉模糊熵公式。

设T={t1，t2，…，tn}且A={|ti∈T}为任意的直觉模糊集，我们构造如下函数：

则有下面的定理成立。

定理1:由上式定义的直觉模糊集A={|ti∈T}的函数E(A)是一个直觉模糊熵。

证明:只需要证明该式满足定义3中的条件(C1～C4)，显然0≤E(A)≤1恒成立。

对于条件(C3)，由于AC={|ti∈T}和式①有

先分别对f(x，y)关于x和y求偏导数，得到

和

2 基于新的模糊熵的直觉模糊多属性决策算法

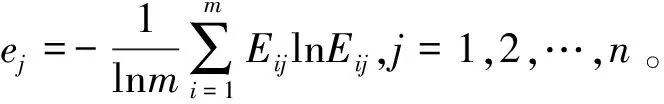
下面给出直觉模糊多属性决策方法。

基于TOPSIS的思想，本文将提出一种基于相似度的直觉模糊多属性决策法。

步骤1:根据步骤1)-3)计算属性权重；

步骤3：分别计算Ai与正、负理想点的Hamming距离d(Ai，A*)和d(Ai，A-)如下。

步骤5：按照相对贴近度Ci越大方案越优的原则对备选方案进行排序和择优。

3 算例分析

选取饲料供应商评价问题作为算例来考察新的直觉模糊决策法的有效性和可行性。设某饲料企业为更好地平抑物价，降低企业成本，提高利润，扩大企业规模，拟对某饲料进行长期采购，由于合同数额较大，合同期较长，因而需要对供应商进行认真筛选，经过历史经验和前期调查，最终确定了4家备选的原材料供应商，分别记为A1、A2、A3和A4，在供应商评价指标选择方面，经过企业领导层讨论，选取如下5个评价指标：o1：质量；o2：价格；o3：准时交货率；o4：交货期和o5：资信度。

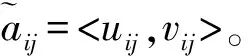
表1 饲料供应商直觉模糊决策信息表

下面将利用本文提出的决策算法对备选饲料企业供应商进行排序和择优。

步骤1：利用上述公式确定属性权重向量为：w=(0.237 8，0.192 2，0.188 7，0.198 3，0.183 0);

步骤3：计算Ai与正、负理想点的Hamming距离d(Ai，A*)和d(Ai，A-)，得结果如下：

d(A1，A*)=0.171 1，d(A2，A*)=0.182 1，d(A3，A*)=0.178 8，d(A4，A*)=0.171 4，

d(A1，A-)=0.552 7，d(A2，A-)=0.525 6，d(A3，A-)=0.554 6，d(A4，A-)=0.570 3。

步骤4：计算第i个方案的贴近度Ci：

C1=0.763 6，C2=0.742 7，C3=0.756 2，C4=0.768 9。

步骤5：按照Ci从大到小排序，得到供应商的排序结果为A4>A1>A3>A2，A4为最佳备选供应商。

4 结语

供应商选择问题包含着多个难以量化的定性评价指标，精确数难以刻画，为此本文发展了基于直觉模糊数的供应商选择模型的多属性决策方法。本文构造了一类新的直觉模糊熵，它可以较好地刻画直觉模糊集的模糊性和不确定程度。同时发展了基于熵的属性权重法和直觉模糊决策法。本文所提出的新的熵测度可以进一步应用到图像处理、模式识别和医疗诊断等领域，新的决策方法还可应用到应急管理决策、风险项目投资等领域，进而为决策者进行决策时提供参考。