自动驾驶车辆对混合交通流的平衡影响研究

王 锋

(甘肃新陆港科技有限公司，兰州 730050)

随着人工智能技术及汽车电子化技术的发展，车辆自动驾驶技术越发成熟，并推动了自动驾驶车辆的快速发展，为缓解交通拥堵带来了新的研究方向。一方面，自动驾驶车辆在路径选择上更加可控，能根据系统算法受中央统一调控；另一方面，由于机器的反应时间更短，且自动驾驶车辆可以同智能基础设施之间进行信息传递，提高道路通行能力[1]。在道路交通网络普及的过程中，自动驾驶车辆会同现有的人工驾驶车辆共存在交通系统内，因此研究自动驾驶车辆对自动-人工混合交通系统出行效率的影响，有利于深入了解自动驾驶车辆对传统道路交通系统的作用。

在现有研究中，国内外学者主要从微观和宏观两方面针对自动-人工混合交通系统展开讨论。

从微观角度来看，已有研究主要采用跟驰模型、元胞自动机模型、深度学习等[2，3]多种研究方法，从多个角度来揭示混合交通系统内各因素之间的相互作用，如Peng等[4]考虑无信号控制的交叉口场景，利用少量具有通信功能的自动驾驶汽车之间的协同控制，同时对人工驾驶车辆进行引导，达到提高混合交通系统出行效率的目的；侯培国等[5]结合跟驰模型和元胞自动机理论，对传统人工驾驶与自动驾驶车辆的混合交通场景进行了建模分析，结果表明自动驾驶车辆比例的增加有利于缓解交通流局部拥堵；Ding等[6]根据车辆的真实跟驰数据，针对包括了人工驾驶车辆在内的混合交通系统，构建了一种改进的Elman神经网络模型实现协同跟车；郝威等[7]考虑车辆的跟随行为，给出了不同出行需求和自动驾驶渗透率下的车辆管理策略，并将其扩展到多车道场景；张林青等[8]利用交通仿真软件对混合交通系统进行了模拟研究，结果表明自动驾驶车辆比例在平峰和高峰状态下对路网交通效率具有不同的影响。

在宏观方面，相关学者更关注混合交通系统内的交通分布状态，以期通过确定不同的交通流分配准则来实现交通流量的均衡分配，如郭宇奇等[9]基于动态图混杂自动机与改进的元胞传输模型相结合的方法，构建了宏观交通流模型来讨论交通路网参数对系统的影响；张传琪等[10]针对不同车辆类型设计了不同的成本函数，并通过奖励机制鼓励出行者乘坐自动驾驶车辆以降低交通拥堵；Sala等[11]针对高速公路这一场景构建了一个广义宏观模型估计车辆排队长度，对混合交通系统进行规划管理；刘诗序等[12]对自动驾驶环境下车辆的路径选择和停车选择方案进行了研究，同时对车辆载人状态和空载状态下交通流之间的相互影响进行了阐述分析。

综上可知，现有研究较少从宏观层面对混合交通系统进行分析，且不同车辆类型的路径选择机制，以及自动驾驶车辆比例增加对混合交通系统的影响也鲜有文献具体阐述。因此，本文针对自动-人工混合交通系统，把从出发点到目的地考虑为固定出行需求，再对车辆的宏观出行行为进行研究分析。

1 问题描述

为阐述自动驾驶车辆加入城市交通网络后对现有人工驾驶车辆出行者路径选择的影响，以及对整个混合交通系统的宏观作用，本文以自动驾驶车辆和人工驾驶车辆为研究对象，探讨不同自动驾驶车辆比例对混合交通系统出行效率的作用。在自动-人工混合交通系统内，自动驾驶车辆受中央统一调控，以系统最优原则进行路径选择；人工驾驶车辆则由出行者进行控制，以用户均衡原则进行路径选择。本文假设单起讫点(origin-destination，OD)间的出行需求是已知并固定的，且在交通网络系统中同时存在自动驾驶车辆和人工驾驶车辆两类出行者。

2 模型建立

2.1 道路网络表示

本文用G(N,A)表示由有限个节点组成的交通网络，其中N表示节点集合，A表示有向线段集合。a为路网中的一条有向线段，xs为路段a上的交通流量，a∈A。W表示OD对集合，w∈W。Krs为OD对w间的可行路径集合，k为一条具体的可行路径且k∈Kw。fw,k为OD对w间路径k上的交通流量。自动驾驶车辆出行者和人工驾驶车辆出行者的出行需求分别表示为

对w间的总出行需求为

路段a上的交通流量为自动驾驶车辆及人工驾驶车辆两类出行者的路段流量之和，其计算公式为

(1)

OD对w间路径k上的交通流量为自动驾驶车辆及人工驾驶车辆两类出行者的径流量之和，其计算公式为

(2)

2.2 人工驾驶车辆模型

人工驾驶车辆由出行者进行操控，在出行过程中，该类出行者一般以个人出行时间最短为路径选择原则，路段a上的出行时间与该路段上的交通流量xa有关。式(3)为美国联邦公路局(Bureau of Public Road，BPR)建议计算路段出行时间的函数：

(3)

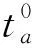
人工驾驶车辆的用户均衡模型如下：

(1) 目标函数为

(4)

(2) 约束条件为

(5)

(6)

(7)

2.3 自动驾驶车辆模型

自动驾驶车辆由中央系统进行统一调控，以系统最优原则进行路径选择，该原则下路段a上的出行成本以边际成本计算，其计算公式为

(8)

自动驾驶车辆的系统最优模型如下：

(1) 目标函数为

(9)

(2) 约束条件为

(10)

(11)

(12)

3 数值仿真与实验

仿真路网拓扑结构如图1所示，路网基本属性如表1所示。由图1可知，节点1、节点4为起讫点，节点2、节点3表示途经路段的节点，路段上标注的数字分别为路段编号、零流阻抗以及路段通行能力。OD对1～4的总交通需求量为3 000 veh·h-1。

图1 仿真路网拓扑结构

表1 路网基本属性

不同自动驾驶车辆比例下的路段流量如表2所示，由表2可知自动驾驶车辆比例分别为10%、50%、90%下不同类别出行者在各个路段上的流量分布情况。当自动驾驶车辆比例为10%时，自动驾驶车辆出行者全部分布在路段1、路段3和路段5，即路径2，人工驾驶车辆出行者则主要分布在路径1和路径3；当自动驾驶车辆比例为50%时，自动驾驶车辆出行者的数量增加，该类出行者主要分布在路径2和路径3，而人工驾驶车辆出行者继续分布在路径1和路径3；当自动驾驶车辆比例增加至90%时，人工驾驶车辆出行者的数量减少，并仅分布在路径1，而自动驾驶车辆出行者则分布在所有路径上。

表2 不同自动驾驶车辆比例下的路段流量

自动驾驶车辆比例对人均出行时间的影响如图2所示。由图2可知，随着自动驾驶车辆比例的增加，人工驾驶车辆出行者及总体出行者的人均出行时间整体呈下降的趋势，而自动驾驶车辆出行者的人均出行时间呈突增与降低交替出现的趋势。在混合交通系统内，自动驾驶车辆以系统最优原则进行路径选择，通过牺牲部分该类出行者的时间使系统出行效率更高，因此对于该类出行者来说，自动驾驶车辆比例的增加并不能使人均出行时间持续降低。对人工驾驶车辆出行者及总体出行者来说，自动驾驶车辆出行者在混合交通系统内的占比越高，系统的出行效率越高，相应的人均出行时间就越低。但当自动驾驶车辆比例超过60%之后，人工驾驶车辆出行者及总体出行者的人均出行时间基本不再发生显著变化。

图2 自动驾驶车辆比例对人均出行时间的影响

自动驾驶车辆比例对路径流量的影响如图3所示。由图3可知，路径3的流量在自动驾驶车辆比例由10%增加至20%时有较大的降低，之后随着自动驾驶车辆比例的增加呈细微变化；随着自动驾驶车辆比例的增加，路径1的流量在逐渐降低之后呈稳定状态，而路径2的流量在逐渐增加之后呈稳定状态。

图3 自动驾驶车辆比例对路径流量的影响

自动驾驶车辆比例对总体出行时间的影响是指随着其比例的增加，路径1上的流量逐渐向路 径2 转移，即路段2上的流量分散到路段3和路 段5，路网中流量分布状态发生变化，出行时间进而发生改变。

为保证结果的无偏性，设定自动驾驶车辆比例为50%，再改变系统内的输入参数总出行需求，出行需求对人均出行时间的影响如图4所示。随着系统内总出行需求的增加，人均出行时间呈指数增长；在总出行需求不超过2 000 veh·h-1时，系统内的人均出行时间不超过20 min，此时交通网络系统处于畅通状态；当总出行需求为3 000 veh·h-1时，人均出行时间约为30 min，此时交通网络系统处于畅通向拥堵转换的过渡阶段；当总出行需求超过3 000 veh·h-1时，人均出行时间显著增加，超过60 min，此时交通网络系统处于拥堵状态。

图4 出行需求对人均出行时间的影响

4 结论

为探究自动驾驶车辆进入城市交通网络后给人工驾驶车辆和交通系统带来的影响，本文以自动驾驶车辆和人工驾驶车辆为研究对象，构建了自动-人工混合交通网络均衡模型，并通过数值仿真试验验证了该模型的正确性和有效性，得出以下结论：

(1) 在混合交通系统内，人工驾驶车辆出行者和总体出行者的人均出行时间整体上是随自动驾驶车辆比例的增加而减少的，而自动驾驶车辆出行者的人均出行时间不随自动驾驶车辆比例的增加而持续减少。

(2) 自动驾驶车辆比例的变化会影响路网中交通流的分配，进而改变混合交通路网中的各路段、路径上的流量分布状态，最终达到优化路网出行效率的目的。

(3) 在固定的自动驾驶车辆比例下，不同出行需求对应着交通路网中的不同路况状态，人均出行时间与系统内的总出行需求呈正相关。

综上所述，在混合交通网络系统中，自动驾驶车辆能提升整个交通系统的出行效率。建议未来道路交通网络发展自动驾驶车辆时，在道路较为拥堵的状态下进行更系统的研究，综合考虑自动驾驶车辆比例这一因素对混合交通系统的影响，并以实际路网进行验证和分析。