基于反步法的多移载工装协同作业编队控制策略

刘禹铭， 赵 勇， 董正建， 王 平， 姬煜琦

(1. 上海交通大学 上海市复杂薄板结构数字化制造重点实验室，上海 200240;2. 上海飞机制造有限公司航空制造技术研究所，上海 201324)

飞机大部件装配作为飞机部装的核心环节，安全高效的部件运输以及自动化高精度的工装对接是整体工作完成的重要保障[1].但是传统的固定平台装配导致工厂场地利用率低，整体装配过程灵活性低，并且装配设备的成本较高，若使用移载工装进行协同装配，则能让工厂的场地利用率和装配效率提高[2].目前大多采用物流作业小车作为作业的移载工装，但是其运动精度较低.当各移载工装由于误差原因导致实际运动位姿偏离期望运动位姿时，多移载工装易使搬运件产生较大内力进而影响装配结果和产品最终的服役性能.

合理的编队控制器能够有效降低队列偏差所导致的作业过程中的内力.由于作业环境的扰动和移载工装的运动误差影响，由多移载工装组成的多智能体系统鲁棒性和稳定性较低，并且具有非线性的特点，而反步法适用于非线性不确定系统的控制，其采取分布式的控制器策略，对多智能体中的每个子系统设计运动控制器[3].Tian等[4]提出了干扰情况下二阶多智能系统的反步法控制方法.Liu等[5]在经典的反步法基础之上，提出有限时间触发方法，减小了通信负担.Xue等[6]则利用滑模控制将状态观测与反步法进行结合，设计了一种自适应反步滑模控制方法.

期望运动状态和实际运动状态是反步法控制策略下的核心变量.对于多智能体的期望运动状态设计依赖于编队方法的设计，目前常用的编队方法主要包括领航跟随法[7]、人工势场法[8]、基于行为控制法[9]、虚拟结构法[10]和虚拟领航者法[11].而其中能够保持队列刚性结构的方法主要为领航跟随法和虚拟结构法.领航跟随法将多机器人作业过程中的编队问题转化为领航机器人和跟随机器人的期望角度与距离之间的关系问题.虚拟结构法的主要理念是将多机器人的队形假设为虚拟的刚性结构进行控制规律设计.该编队方法下整体队形轻便，形成稳定队列的收敛时间快，但系统稳定性难以保证，鲁棒性和灵活性较差[12].基于多移载工装进行协同装配时的刚性队列要求和不同工厂环境下模块化装配的需要，将虚拟结构法和虚拟领航者法相结合，以虚拟结构的参考点作为虚拟领航者进行作业运动规划.常用的运动规划算法有人工势场法[13]、A*算法[14]、遗传算法[15]、粒子群优化算法[16]等.人工势场法的运动规划兼容编队控制和避障规划的要求，且具有计算量小、规划路径平滑易于设计轨迹追踪器的优点，被广泛运用于工程实践中.编队控制的另一个重要环节是实际运动状态的估计，通过测量设备的定位与滤波算法的结合，实时校正估计实际位置.而针对移动机器人的定位领域，基于粒子滤波算法进行定位最为广泛.粒子滤波以其具有多模态、统计特征随机分布的特性，适用于位姿估计和实时目标追踪.但是粒子滤波过程中重采样会导致粒子退化的问题，针对这一问题，赵国旗等[17]将模糊理论引入粒子滤波来防止重采样中出现的多模态失效的问题.Li等[18]针对粒子滤波结合引入基于库尔贝克-莱布勒散度(Kullback-Leibler Divergence, KLD)进行采样的方法，有效解决了粒子退化问题.

本文以反步法作为编队控制策略的基础，将虚拟结构法和虚拟领航者法相结合，通过改进的人工势场法和纯轨迹跟踪法设计虚拟领航者的期望运动位姿，解决了路径规划陷入局部最优的问题，进一步根据队形几何关系推导得到实际跟随者的期望运动位姿.结合雷达测量设备和自适应蒙特卡洛定位(Adaptive Monte Carlo Localization, AMCL)算法估计实际运动位姿，降低了每个移载工装的定位误差值，基于跟随误差设计了队形控制器，完成了队列的协同作业控制.

1 基于反步法的编队控制器设计

1.1 结合虚拟结构法和虚拟领航者法的队形设计

在协同搬运机翼的过程中，移载工装需要保持编队队形的刚性结构，以减小队形变形所产生的误差进而降低内力.编队结构的队列模型如图1所示.

图1 虚拟领航者引领下的刚性结构队形Fig.1 Rigid structure formation guided by virtual navigator

考虑以期望队形的几何中心作为编队参考点，在该位置添加一台同类型的虚拟移载工装，即虚拟领航者.实际的移载工装作为跟随者，进行整体的编队控制，领航跟随的关系如图2所示.其中，C为小车质心，w为角速度.

图2 领航者与跟随者编队位姿误差分析Fig.2 Pose error analysis of leader and follower formation

假设领航者机器人i在全局坐标系中对应的坐标为(xi,yi)，则由图示的几何关系可以得到全局坐标的变换关系：

(1)

(2)

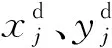
由式(1)与(2)可以得到移载工装期望位姿以及实际位姿.将两式相减，得到误差的相应关系式并将其对时间求导，进一步获得误差关于时间的微分方程，从而根据队列的运动误差，设计队形控制器.

(3)

(4)

1.2 基于反步法的跟随者队形控制器设计

针对编队中各个跟随者产生的运动误差，设计基于反步法的分布式队形控制器.反步法应用于非线性系统的一般形式为

(5)

式中：fx(x)和gx(x)为与输入变量x相关的函数；ux(x)为输入控制量.根据已得到的误差动态微分方程，将xe、ye两项误差值看作队形控制器的子系统，并递归寻找对应的虚拟控制，对于两项输入控制vj和wj，当选取vj作为虚拟控制输入时：

(6)

(7)

当ye=0时，V1≤0，则xe在有限时间收敛至0.对于下一个子系统微分方程的虚拟控制量wj，设计取值为

(8)

(9)

2 移载工装的运动轨迹规划与运动状态估计

2.1 基于改进人工势场法的避障路线设计

从整体队列控制器的设计过程可知，期望的运动状态和实际的运动状态的求取是控制的两大关键.期望的运动状态需要满足避障、运动平滑、对不同作业环境规划适应性强的要求，而求取实际的运动状态需要满足实时性强、精度高的要求，通过两者决定的运动误差来设计可用的队列控制器.整体的设计流程图如图3所示.

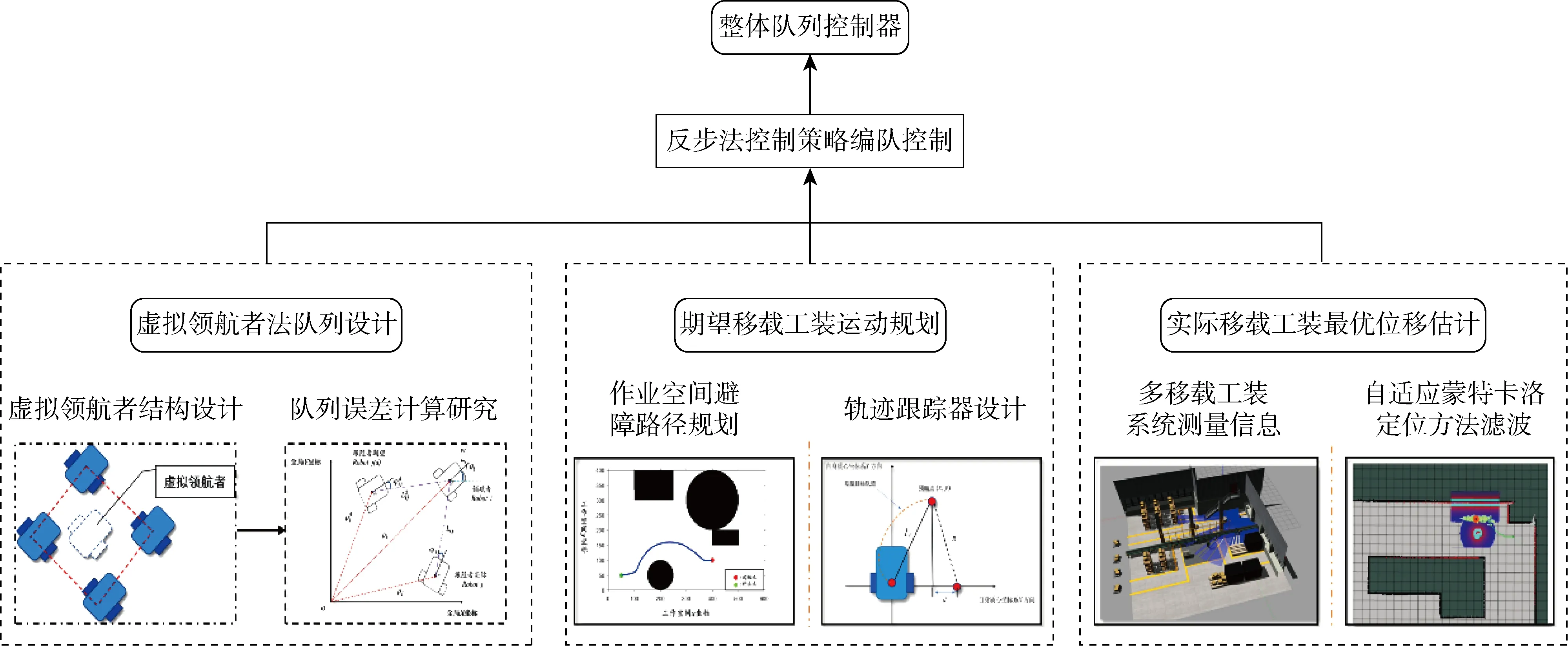
图3 整体编队控制器设计流程图Fig.3 Designed flow chart of overall formation controller

根据编队控制器的设计流程，首先进行虚拟领航者的期望运动路径设计.基于实际工作环境扫描得到多移载工装的作业空间，在作业空间中引入人工势场，障碍物周围分布斥力场，目标点周围分布引力场，使得被控对象在合力作用下自主移动.设定移载工装所在位置为q(x0,y0)，目标点位置为g(xend,yend)，定义目标距离函数为ρ(q,g)，q为起始点，g为目标点.在传统的人工势场中常用的引力与斥力场函数为

(10)

(11)

式中：η、ξ为选取的引力系数与斥力系数；ρ(q)为移载工装距离障碍物最近点的距离；q0为基于移载工装自身尺寸以及队形等要素所决定的安全距离.而斥力场仅在针对移载工装定义的安全距离内生效，以达到更短的避障路线规划.由于虚拟领航者位于队列几何中心，所以选取几何外接圆半径为安全距离的参考基准，能简洁地处理编队避障的问题，路径规划的场地适应性和实时性都能满足要求.

图4 结合模拟退火法的人工势场法算法流程图Fig.4 Algorithm steps of APF method in combination with simulated annealing

使用上述介绍的改进人工势场法，当虚拟领航者陷入局部最优导致运动震荡时，通过搜索下一路径点进行跳出，如图5所示.

图5(c)与5(f)中的箭头符号象征人工势场中的势场矢量，而图5(d)中的U为合势场的大小，没有对应的单位.可以看出，采用模拟退火法使得被控移载工装在全局坐标系中跳出了局部最优点，重新规划路径，最终到达了目标点.

图5 模拟退火法逃出局部最优示意图Fig.5 Diagram of escaping from local optimum by simulated annealing

2.2 移载工装预期轨迹的追踪控制器设计

使用改进人工势场法规划虚拟领航者的避障路径之后，需要设计对应的轨迹追踪控制器保障移载工装的循迹作业.设计轨迹跟踪器需要先构建移载工装的运动学模型.实际作业环境下的移载工装的运动可忽略竖直方向上的运动，因此将被控对象的运动空间设计成二维平面.基于实际工况，在控制移载工装的过程中，根据已有移载工装的实际参数和控制变量，输入对应的移载工装角速度和线速度，并将移载工装简化为图6所示的差速轮驱动模型，图中：XL和YL为小车以质心C所建立的坐标系X轴与Y轴；r为小车差速轮半径；2Ra为小车的宽度；p为小车车轮车轴的中心点，D为小车质心C离轮轴中心的距离.

根据图6建立的运动学模型，假定移载工装为差速轮，其对应整体工装的控制量为[vw]T，即运动速度v和决定方向的角速度w.而相对应的状态变量为[xyθ]T，即全局坐标系下的x和y以及行驶方向与X轴正半轴的夹角.在图6中，移载工装的质心在平面坐标系下的速度为vc，其在X,Y上的分量为vxc与vyc，则通过速度分解：

图6 移载工装简化的运动学模型示意图Fig.6 Schematic of simplified kinematic model of transfer tooling

vxccosθ+vycsinθ=v

(12)

通过简化模型几何关系可以得到差速轮模型的移载工装运动方程，写作整体系统方程形式:

(13)

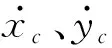
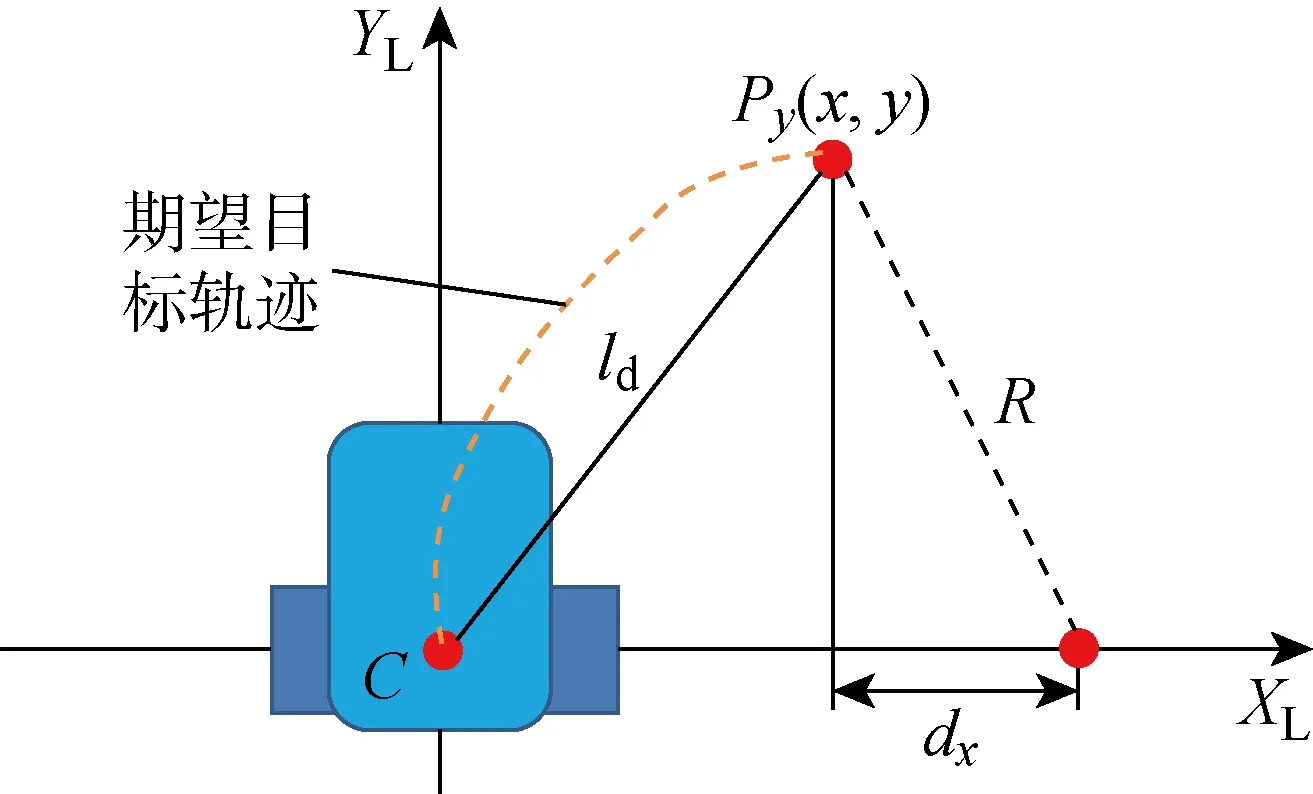
图7 纯轨迹跟踪法的几何关系示意图Fig.7 Geometric relationship schematic of pure pursuit tracking method

根据图7的几何关系可得距离方程：

(14)

并得到相关曲率的表达式和角速度控制方程：

(15)

通过选取较为平缓的速度和合适的预瞄距离来选取相关的输入控制量，从而确保对运动轨迹较好的追踪效果，并得到虚拟领航者的规划运动状态，根据提出的队形结构的几何关系变化，进一步计算跟随者的期望运动状态.

2.3 基于自适应蒙特卡洛算法的位姿估计

移载工装的实际位姿是队形偏差计算的另一个关键元素.若直接采用测量设备进行定位获取实际位姿，传感器的误差会直接影响定位的结果，进而导致队形偏差计算失准.而结合滤波算法修正观测变量的定位方法可以提高实际运动状态的观测精度，解决定位精度不够的问题.本文构建移载工装的实时定位框架，采用自适应蒙特卡洛定位算法进行实际位姿估计.

蒙特卡洛定位(Monte Carlo Localization, MCL)算法是一种适用于室内较小地图情况下的全局定位算法.该算法基于概率进行定位计算，使用粒子表征移载工装所处位置的概率大小，初始时刻粒子平均分布在全局地图上，在移载工装运动作业时，粒子与移载工装同步运动，并根据移载工装的位姿筛选出与移载工装运动状态一致的粒子.在一段时间后粒子完成收敛时，当前粒子即表征移载工装的真实位姿估计，若粒子收敛后表征的位姿是错误的，该算法无法做到纠偏和恢复.当粒子数目较少时，丢失真实位姿附近的粒子的情况常有发生.而AMCL算法的引入有效地规避了这一问题.自适应蒙特卡洛定位算法是蒙特卡洛定位算法的一种改进.AMCL通过KLD重采样的方法注入了新的随机粒子，减小粒子运算量的同时，避免移载工装“绑架问题”的出现.

首先针对移载工装的运动状态和观测状态进行建模，其状态方程为

(16)

(17)

(18)

而移载工装的运动状态的后验可靠性估计为

(19)

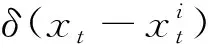
(20)

式中：Mχ为粒子集的数目阈值；k′为非空粒子状态空间的个数；ε与β分别为真实分布与预估分布的最大误差与正态分布的分位数.根据KLD采样的流程可以看出，当粒子对整体地图覆盖程度高时，采样的粒子集数目降低，可以减小实时定位过程中的运算量；而粒子对地图覆盖程度较低时，粒子数目提高，在误差协方差较低的情况下通过随机引入粒子的方法防止重采样过程中粒子退化的问题.如图8所示，AMCL算法运用于移载工装全局定位并最终收敛，收敛粒子表征移载工装的估计位姿.

图8 AMCL算法的定位收敛过程Fig.8 Location convergence process of AMCL algorithm

本文通过融合移载工装的里程计与激光雷达的传感器信息，将移载工装运动模型和观测模型代入AMCL算法，提出合理的粒子提议分布来逼近移载工装的位姿，其具体估计流程架构如图9所示.

图9 AMCL算法运用于移载工装协同作业的定位流程Fig.9 Positioning process of AMCL algorithm applied to collaborative operation of mobile robot

3 仿真验证

3.1 仿真环境搭建以及参数设计

通过在ROS-Gazebo中建立与现场环境相关的实际地图和差速轮移载工装模型，并进一步将实际地图二值化，得到如图10所示的场景图，将规划的路径点与控制信号发送给移载工装进行编队位移控制.并在ROS中构建在该场景下多移载工装的仿真模型.

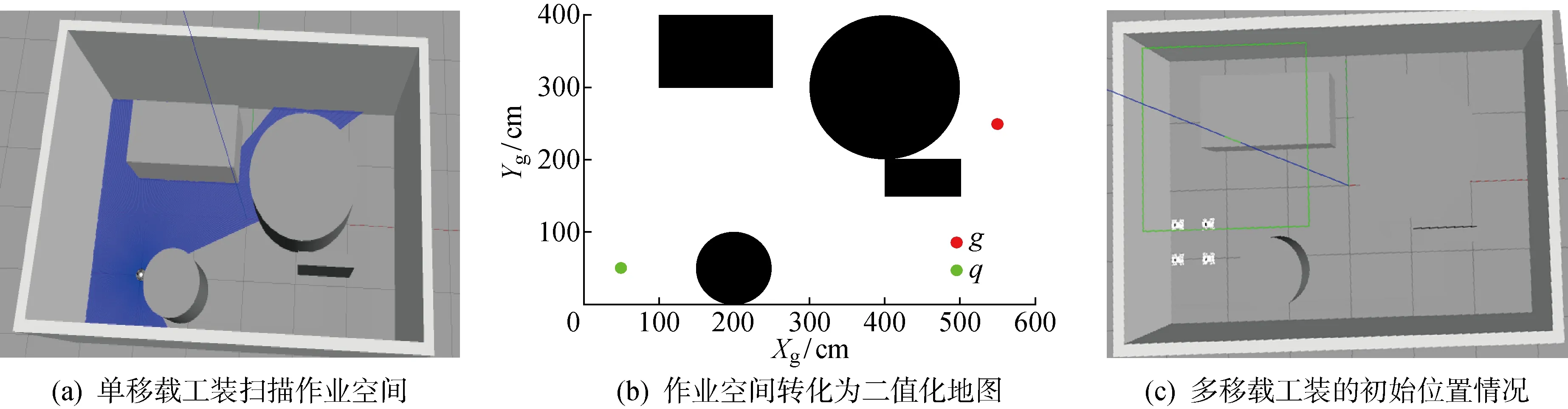
图10 仿真作业空间建模Fig.10 Construction of workspace simulation environment

根据搭建好的二值地图，通过改进人工势场法来规划虚拟领航者和跟随者的期望路径.其中载工装的具体参数以及队列期望距离如表1所示，导航方式为激光定位与第一构建，并得到相应的虚拟结构刚性队列的几何中心路径图.

表1 移载工装技术参数Tab.1 Technical parameter of transfer tooling

在移载工装的运动空间中建立引力、斥力场，选取的引力系数η=1/70，斥力系数ξ=8/7，虚拟领航者与作业空间中障碍物的安全距离根据队列距离与自身尺寸设置为35 cm.作业空间内的总体引力场、斥力场以及总势场如图11所示，图中：Urep为作业空间内的斥力；Uatt为作业空间内的引力.

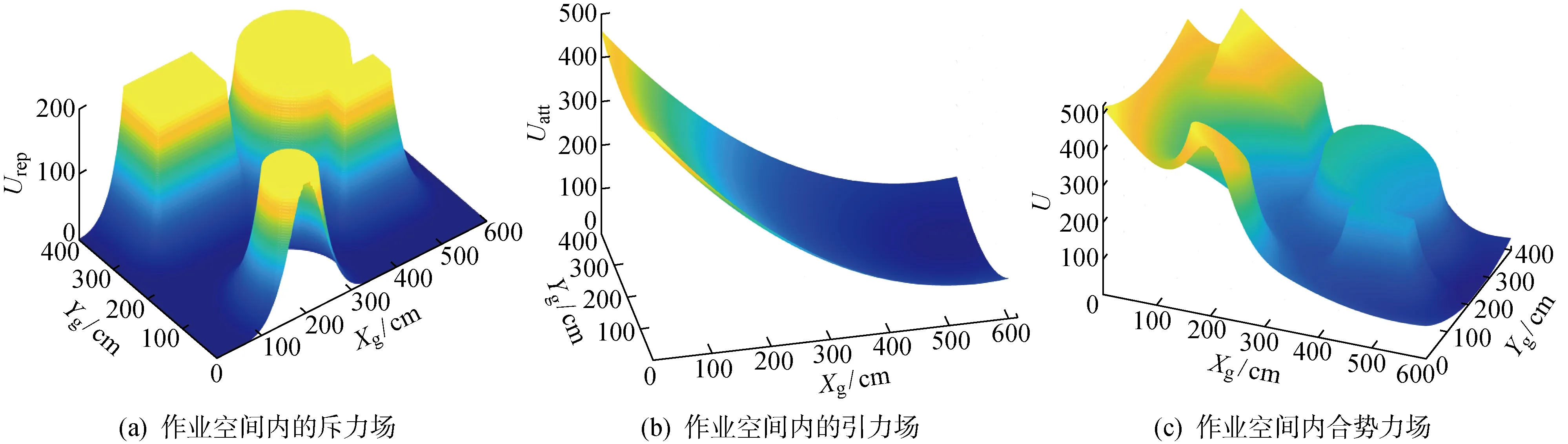
图11 移载工装作业空间内势场变化图Fig.11 Variation diagram of potential field in workspace of multiple mobile robots

通过给定参数的移载工装，在Simulink中建立符合标准的基于差速轮驱动的移载工装运动模型，并对期望轨迹通过纯跟踪法进行追踪，得到虚拟领航者相应的期望速度与角速度如图12所示，其中设定预瞄距离下限值为5 cm.

图12 差速轮移载工装运动模型Fig.12 Motion model of differential wheel transfer tooling

对于整体的测量系统，采用车载激光雷达的出厂误差作为测量误差，结合实时控制的运动方程产生的误差进行滤波从而对实际位姿与运动状态进行估计与修正.其中距离测量误差的初始提议分布为N(μ1，σ1) (μ1为均值，σ1为方差)，角度测量误差的初始提议分布为N(μ2，σ2) (μ2为均值，σ2为方差)，均假设为高斯分布，协方差与均值由表1参考获得.得到实际跟随者移载工装的状态变量最优值后，再通过反步法设定的控制策略，进行队列的纠偏仿真.

3.2 仿真结果分析

在进行避障路径规划中使用传统人工势场法，即不引入模拟退火法逃离局部最优点时，在目标点靠近障碍物的过程里，移载工装会陷入势场中的局部最优点而小距离震荡，最终无法到达目标点.移载工装在势场中停滞情况与整体路径如图13所示.

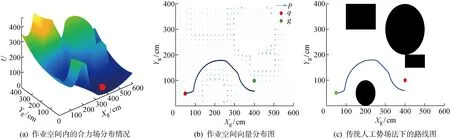
图13 传统人工势场法下失败的路径规划Fig.13 Failed path planning in traditional artificial potential field method

结合模拟退火法对陷入局部最优的情况进行了改进.设定停滞震荡的距离判定范围为3 cm，并进行模拟退火法进行跳脱，其改进后路线如图14所示.

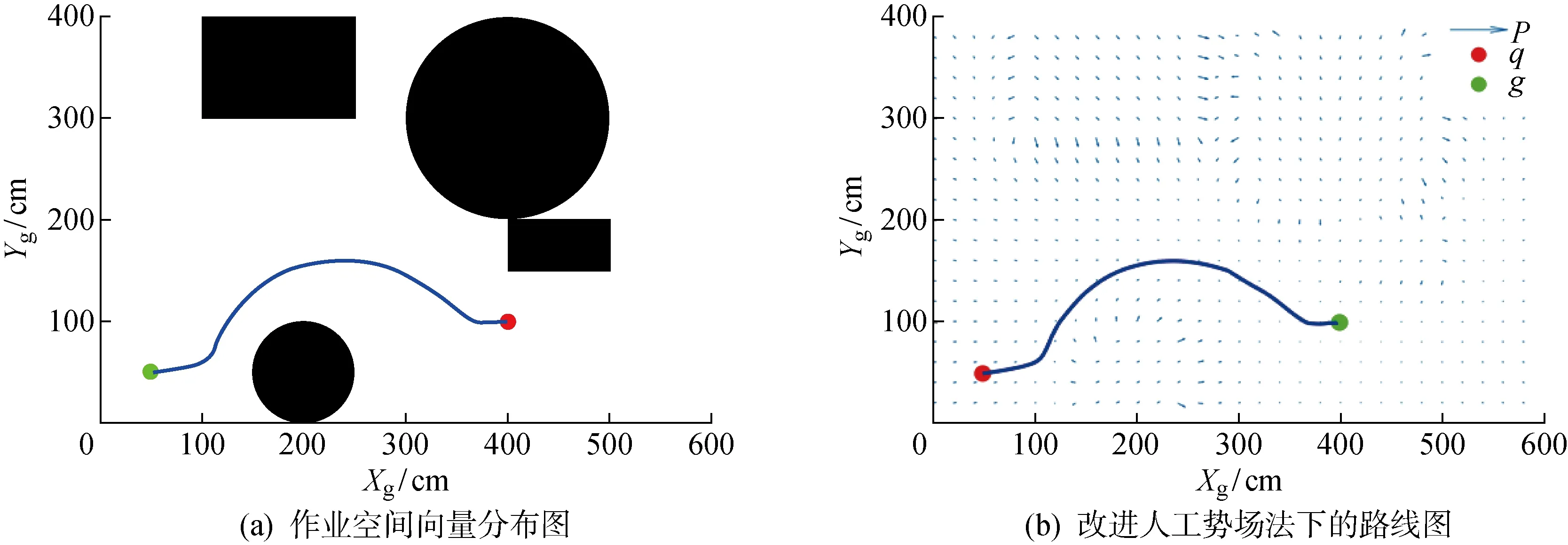
图14 改进人工势场法成功规划目标路径Fig.14 Target path planed by improved artificial potential field method

设定预定路径之后，使目标小车模型对路径进行了轨迹追踪，保持领航者速度10 cm/s匀速行驶进行编队控制，通过计算得到的输入控制量如图15所示，图中：T为控制时间.

图15 虚拟领航者输入运动变量Fig.15 Input movement variables of virtual pilot

确定系统输入控制量后，使用Simulink搭建的移载工装纯轨迹跟踪法模型进行轨迹追踪仿真，得到图16所示的追踪效果和对应误差图像，图中E为移载工装跟踪运动误差.仿真结果表明，输入控制的角速度变化较平缓，追踪偏差逐渐收敛于2.2 cm以内，满足追踪的需求.

图16 纯轨迹跟踪下的期望轨迹与误差Fig.16 Desired trajectory and error in pure trajectory tracking

在仿真环境中读取移载工装的实际位姿，以激光雷达作为测量设备.根据蒙特卡洛定位以及自适应蒙特卡洛定位方法估计移载工装的实际位姿，并与直接使用激光雷达测量的方法进行对比，结果如图17所示，图中：Eθ为角度追踪误差；Edis为距离跟踪误差.对比可得，使用自适应蒙特卡洛定位的方法可以将角度误差降低到0.01° 以下，比直接使用测量设备的0.5° 测量误差有较大降低.距离方面也将误差收敛在0.8 cm以内，两者的误差协方差系数也相较于MCL定位算法和直接使用测量设备进行定位的误差协方差系数小.

图17 自适应蒙特卡洛定位方法误差与其他方法误差对比Fig.17 Comparison of error of adaptive Monte Carlo localization method and other methods

利用反步法设计的控制策略对整体队形进行保持.对于反步法中k1和k2参数的选取，由于4台实际跟随者关于虚拟领航者几何对称，基于误差的控制策略可选取相同参数，所以k1和k2参数只需要对单台跟随者进行设计，引入表征控制效果的指标：

(21)

式中：Δx、Δy及Δθ为实际运动与期望运动的误差值；α为比例系数，取60，并将符合收敛的参数域中的指标进行归一化：

(22)

式中：Si为第i台移载工装的评价指标归一化结果；si为第i台评价指标结果；S为多移载工装评价指标之和.通过仿真得到不同参数变化情况下，移载工装在跟随过程中的评价指标变化情况，如图18所示，并选取指标极大值位置的参数值为[1.02, 1.47]，即反步法中的控制参数[k1,k2], 红点为极大值.

图18 反步法控制效果与参数选取关系Fig.18 Relationship between backstepping control effect and parameter selection

图19 跟随者理想运动轨迹设计Fig.19 Ideal movement trajectory design of follower

表2 跟随机器人三方向追踪时间Tab.2 Track time in three directions of robot follower

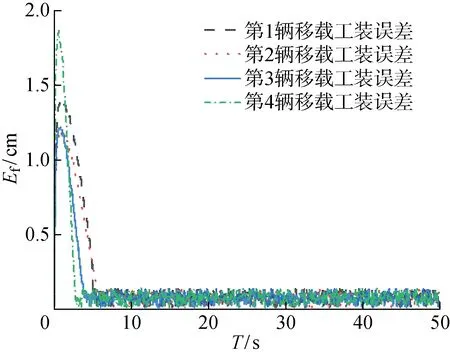
图20 跟随者误差指标随时间变化曲线Fig.20 Follower error metric versus time

可以看出，在控制量有一定的扰动下，移载工装依然能够在6.2 s内收敛到期望的位姿，达到整体的编队要求.

4 结语

针对多移载工装协同作业的控制问题，提出了一种基于反步法的多移载工装协同作业编队控制策略.建立了移载工装的运动学模型，提出了基于改进人工势场法和纯轨迹追踪法的期望运动状态规划方法，以及基于自适应蒙特卡洛定位的实际运动状态估计方法，与直接使用测量设备相比，角度误差由 0.5° 降低至 0.01°，位置误差由2 cm降低至 0.8 cm，精度提高.构建了仿真模型进行验证，队形误差在6.2 s内达到收敛，满足多移载工装协同作业的条件.