一种V2X环境下基于改进卡尔曼滤波的CACC数据精度提高方法

赵红专，卢宁宁，陈建鹏，展 新，许恩永

(1. 桂林电子科技大学 建筑与交通工程学院，广西 桂林 541004；2. 东风柳州汽车有限公司 商用车技术中心，广西 柳州 545000)

0 引 言

典型弯道区域因驾驶员视距受限和曲线线性特殊性，车辆间需要通过信息进行频繁的交互以获得各自可靠信息和可信服务，实现有效协同。统计表明，弯曲、起伏路段发生的交通事故中，三分之二以上的事故发生在弯道区域；相关资料表明[1]，弯道区域的事故发生率是其他路段的两倍以上，其机动车事故死亡人数约占总机动车事故死亡人数的四分之一。

V2X (vehicle to everything, V2X)通过车载传感器设备检测前车行驶状态的信息，并将前方车辆行驶过程中的速度、加速度、位置等信息传递给本车，为CACC (cooperative adaptive cruise control, CACC)车队中车车信息传递和信息交互提供技术支撑。车辆通过V2X技术实现车车互联通信[2]，以便能够有效获取道路周边信息和车辆实时驾驶数据，从而提高道路吞吐量和交通安全，提高驾驶员的舒适性。弯道中行驶的车辆因各种因素无法保持车道行驶，从而偏离车道，引发车辆碰撞[3-5]；CACC系统通过多种传感器感知周围车辆的行驶状态和路况[6]，为本车获取前方车辆实时行驶数据提供技术支持，有效减少车辆间的行驶安全距离，为车路协同控制提供保障。

CACC车辆间进行信息频繁交互过程中，会存在通讯延迟和信息交互不可信等问题。笔者团队[7]为解决交通动态条件下信息交互的可信性问题，提出了一种基于车辆信息物理系统的车辆自组织机制的新信任模型，该信任模型可以提高车辆交互安全和驾驶安全。但是信息在数据传输的过程中，仍存在环境噪声、系统误差、数据传输的可靠性等使传感器获取的数据存在噪声[8]等不利因素，进而影响CACC车队的安全行驶。

目前关于CACC车队行驶特性的研究较多，如车辆跟驰、车辆渗透率等方面研究，很少关于车辆在弯道的行驶状态的研究，目前研究也没有考虑获取的数据精度对车辆行驶的影响。笔者根据车载设备获取的前方车辆信息通过V2X技术传递给本车，在此过程中采用基于速度方位角变化的改进卡尔曼滤波算法处理此数据，以提高车辆行驶的数据精度。

1 CACC车辆的弯道行驶特性

研究CACC车辆的行驶状态有利于车辆遇到突发状况时起到预警作用。ZHU Meixin等[9]建立了前方碰撞预警系统，该系统通过车头时距估计距离和速度的变化，以便驾驶员在行驶过程中遇到突发状况时及时地做出反应；Z. CHEN等[10]通过判定CACC车队中前方车辆的3种情况，即基于位置的前方车辆、基于距离的前方车辆、基于位置和距离的前方车辆，提高了车辆的识别精度和距离；C. M. HUANG等[11]通过研究碰撞预警中车辆速度变化、曲线道路状况、GPS(global positioning system，GPS)引起的位置中断，提出了一种基于矢量的碰撞系统，试图解决上述挑战和实现有效预警；ZHANG Ruifeng等[12]提出了一种基于加速度的车辆碰撞预警算法，以提高碰撞检测的准确性。上述的研究均基于已有的数据或通过传感器测得数据进行验证分析，没有对数据是否存在噪声做详细处理，具有理想化。

CACC车队在行驶过程中通过雷达或传感器实时获取周围环境(道路、建筑、行人、车辆等)和运行控制中端等信息，决定自身的行驶路径、加速度和速度等因素[13]。通过分析CACC车队在弯道行驶的轨迹，以车辆间几何关系为基础分析车队的弯道行驶状态。

选取CACC车队中某一车辆i为坐标原点建立直角坐标系，平行于车辆行驶方向为x轴，如图1。

图1 CACC车辆在弯道行驶中坐标系的建立Fig. 1 Establishment of coordinate system of CACC vehicles driving on curves

根据微积分原理，将车辆在行使过程中的轨迹分割成多个线段(例如0.01 s内的行驶轨迹)，则这些线段可以近似看作直线。通过车辆安装的雷达传感器测量前车相对本车的方位角和距离，再通过三角函数得出车辆间的几何关系，进而预测前方车辆相对自车的坐标位置：

(1)

式中：f(xi+1，yi+1)为目标车辆相对自车的坐标；αi为自车到目标车辆坐标系方位角；Li为车辆间直线距离。

根据递归思想，目标车辆k相对自车k-1的坐标为：

(2)

式中：f(xk,yk)为第k辆车相对第k-1 辆车的坐标；αk为第k辆车相对第k-1 辆车的位置方位角；Lk为第k辆车与第k-1 辆车之间的直线距离。

做垂直于车辆速度行驶方向的垂线，两车之间的垂线相交于O′点，对应的夹角为θi(图1)，对应的半径设为:

(3)

根据自车和目标车辆的速度矢量关系，得到：

(4)

式中：θi=βi=φ+φ0。

根据三角函数关系可知：

(5)

根据三角函数关系，当αi，φ，φ0，βi足够小时，可以得到近似值：

(6)

(7)

|α0|=φ0

(8)

车辆在弯道行驶的几何特性可得：

(9)

车辆之间通过θi进行位置判断，车辆行驶过程中t-1时刻横向变化为：

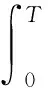
(10)

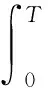
(11)

xer,t=xk,t-xreal,k-1,t

(12)

式中：xreal,k-1,t为两车之间的纵向真实距离；xev,k-1,t为两车之间的期望距离；xk,t为第k辆车在t时刻相对于自车k-1的横向坐标；xk-1,t-1为第k-1辆车在t-1 时刻相对于自车k-2的横向坐标；vk-1,t-1为第k-1 辆车在t-1时刻的速度；T为t-1到t时刻的时间间隔；xer,t为两车之间的间距误差。

2 改进卡尔曼滤波算法

通过分析车辆在弯道行驶的几何关系，在原有卡尔曼滤波基础上考虑了车辆速度方位角的变化，将车辆行驶过程中的变化与改进卡尔曼滤波算法相结合，使改进的卡尔曼滤波算法适用于弯道行驶的CACC车辆，进而提高中低速环境下CACC车辆在弯道行驶的数据精度，保障车辆在弯道行驶的稳定性和驾驶员舒适性。

2.1 数据处理方法概述

CACC车队在行驶过程中通过传感器获取周围车辆行驶信息并通过V2X技术将获取的信息传递给本车，获取的信息包括车辆间的距离和车辆行驶速度、加速度、车辆周围行驶环境等特性。但车辆响应、传感器、信息传递延误等因素使获取的数据存在噪声，为了提高CACC数据精度，需要对数据进行滤波处理。

目前车辆状态信息估计研究方法主要为卡尔曼滤波算法及其各种改进算法。据调查发现[14-15]，卡尔曼滤波算法广泛应用于评估交通密度，使之获得比原始数据更高的精度；同时在车辆跟踪方面，卡尔曼滤波通过此刻获取的数据对下一刻进行预测和减少长期跟踪带来的误差问题[16]。卡尔曼滤波算法是一种最优化的递归数字处理的算法，不仅是一般的滤波器，更像是一种观测器，具有较高的精度。

2.2 基于速度方位角的改进卡尔曼滤波算法

车辆在弯道行驶过程中速度方位角和传感器获取的车辆横向坐标为xk,t，根据式(10)和式(12)可得：

xk,t=xk-1,t-1+(1-cosθ)vk-1,t-1T

(13)

车辆在t-1时刻到t时刻的加速度为ak,t-1，则车辆在间隔T时刻的位置、速度为：

(14)

(15)

式中：加速度ak,t-1由自车加速度uk,t-1和随机加速度wk,t-1两部分组成；uk,t-1、wk,t-1分别符合标准正态分布，协方差矩阵分别为Q，R。

ak,t-1=uk,t-1+wk,t-1

(16)

式中：uk,t-1表示CACC车辆在t-1时刻自身产生的加速度，该值在T时刻内可以看作是一个常量，在此过程中会产生过程误差wk,t-1；wk,t-1为外力产生的干扰加速度。

CACC车队行驶状态如图2。设采样时刻k处车辆运动的状态方程为：

(17)

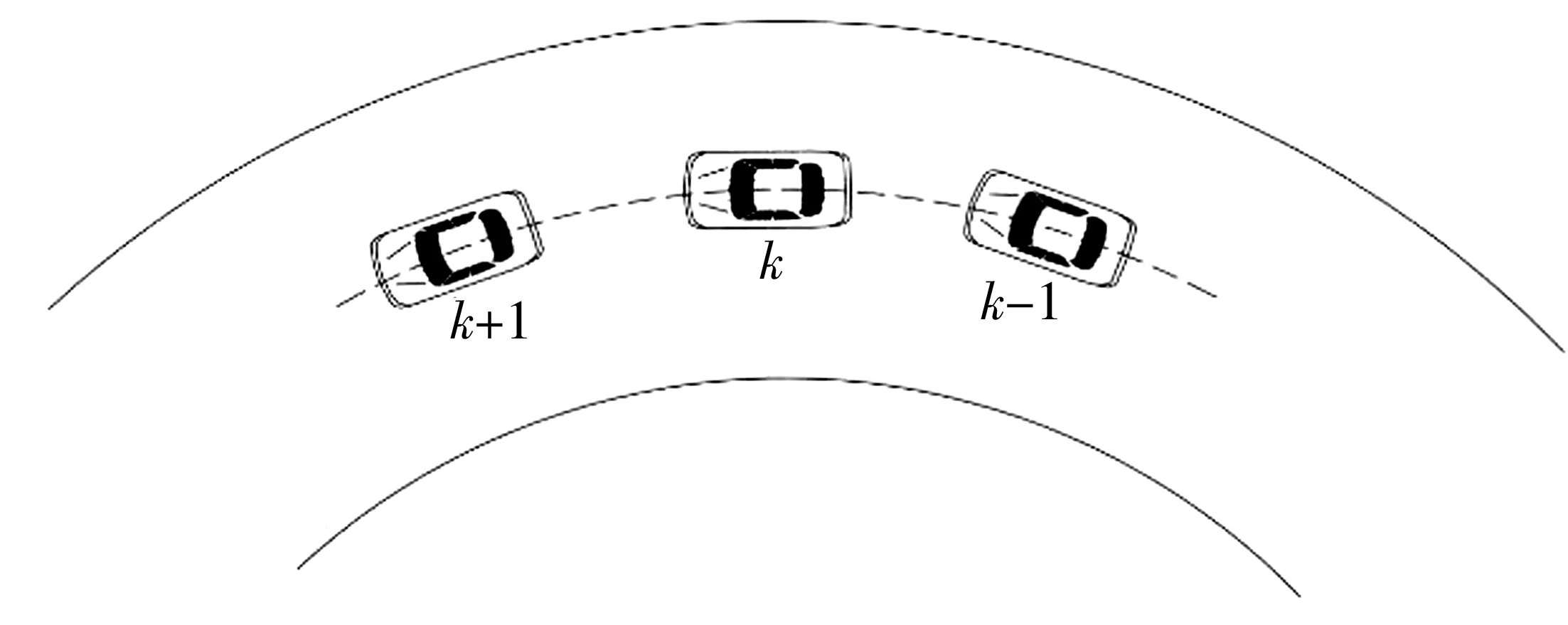
图2 CACC车队行驶状态Fig. 2 Driving status of CACC fleet

观测方程：

(18)

车辆状态空间模型为：

yt=Φxt-1+But-1+Γwt-1

(19)

xreal,t=xt-1+xt-1Tcosθ

(20)

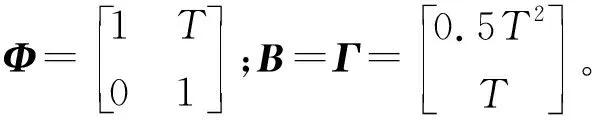
故根据车辆速度方位角θ建立的改进卡尔曼滤波模型得出：

1)先验状态预测方程：

(21)

2)先验误差协方差：

(22)

式中：

3)经计算化简得卡尔曼滤波增益方程：

(23)

4)后验状态更新方程：

(24)

5)更新误差协方差方程：

(25)

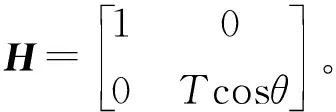
3 实验验证

为提高CACC车辆在弯道的行驶安全性和舒适度，在保证数据可信的情况下，将获取的数据经过改进卡尔曼滤波后模拟CACC车辆在弯道行驶的过程，进而分析车辆间行驶数据经过有无改进卡尔曼滤波后对车辆行驶速度、加速度等状态的影响。

3.1 数值仿真参数设置

V2X环境下CACC车辆在行驶过程中，通过改进卡尔曼滤波算法处理CACC车辆自身传感器获取前方车辆的速度、加速度、车辆间的距离等数据。设计数值仿真实验时，考虑到CACC车辆在行驶过程中，车车之间信息传递存在通讯延迟，文献[17]研究端到端通信延迟为20 ms，故此次仿真过程中将CACC车辆通讯延迟设置为20 ms。根据弯道限速和文献[18]仿真工况，仿真实验场景设置为车辆在中低速情况下行驶，车辆在初始时刻设置40 km/h的行驶速度，以a=sin(0.3t)模拟车辆在弯道中不断变化的加速度，m/s2，具体参数设置如表1。

表1 交通仿真中参数取值Table 1 Parameters value in traffic simulation

3.2 数值仿真结果分析

由于通过车载传感器获取的数据存在噪声，所以在仿真过程中采用传统卡尔曼滤波和笔者建立的改进卡尔曼滤波算法处理的数据与真实值xreal进行比较。主要分析CACC车辆在弯道行驶过程中有何变化，进而判断改进卡尔曼滤波算法是否提高数据精度。为易于判断车辆行驶过程中横向位移的变化和改进卡尔曼滤波处理数据噪声是否有效，选取部分时间内的车辆横向位移变化进行分析。

通过对比改进前后卡尔曼滤波对车辆行驶横向位移的影响，进而判断改进后的卡尔曼滤波对车辆行驶是否有影响。从图3可知，真实值、滤波前、滤波后相对平缓，没有较大的变动，但是滤波后的数值更接近真实值；而图4中，滤波前的数值在真实值附近上下波动，波动范围较大，滤波后的数值接近于真实值，具有较好的滤波效果。

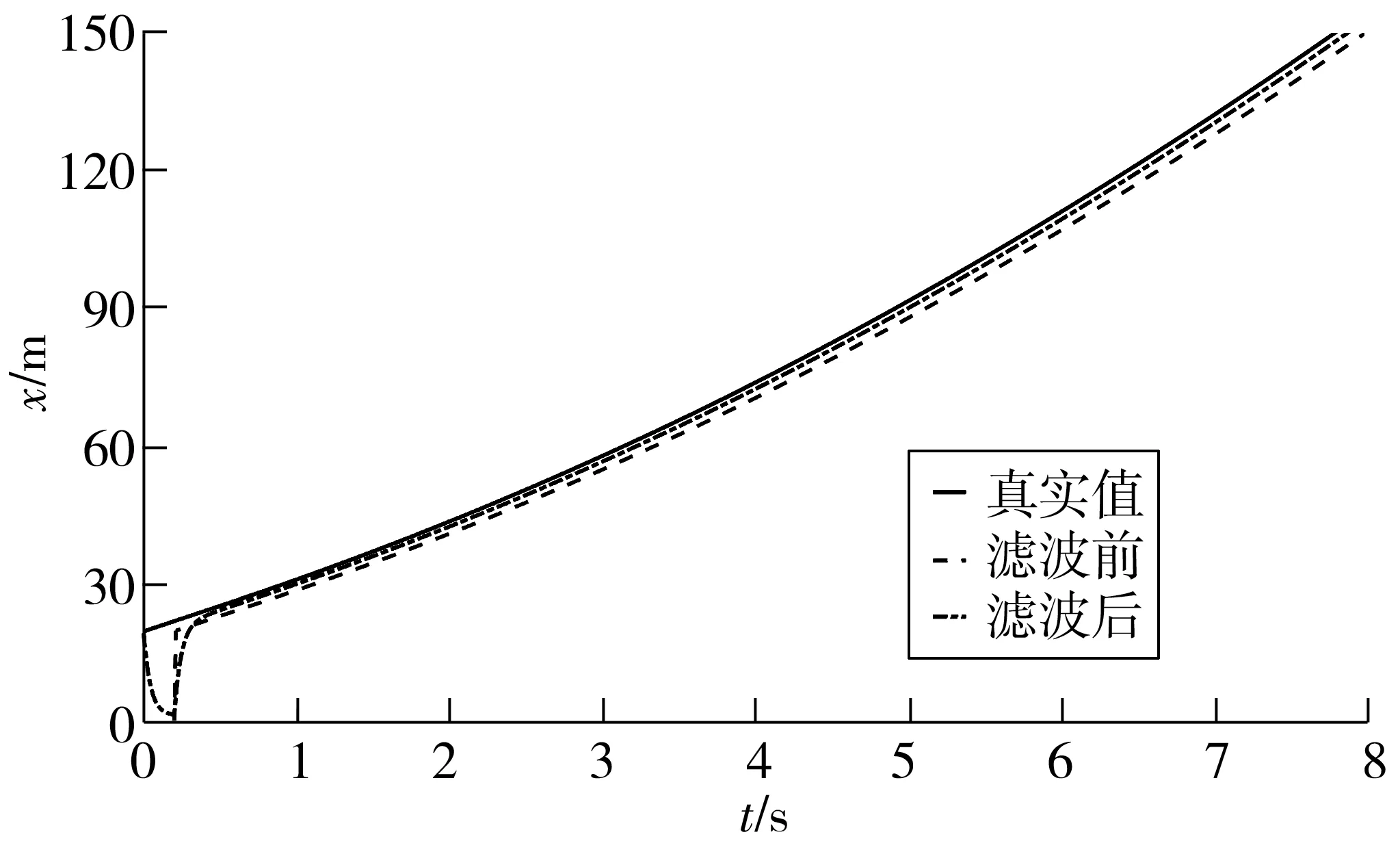
图3 卡尔曼滤波后车辆行驶横向位移曲线变化Fig. 3 Variation of vehicle lateral displacement curve after Kalman filtering

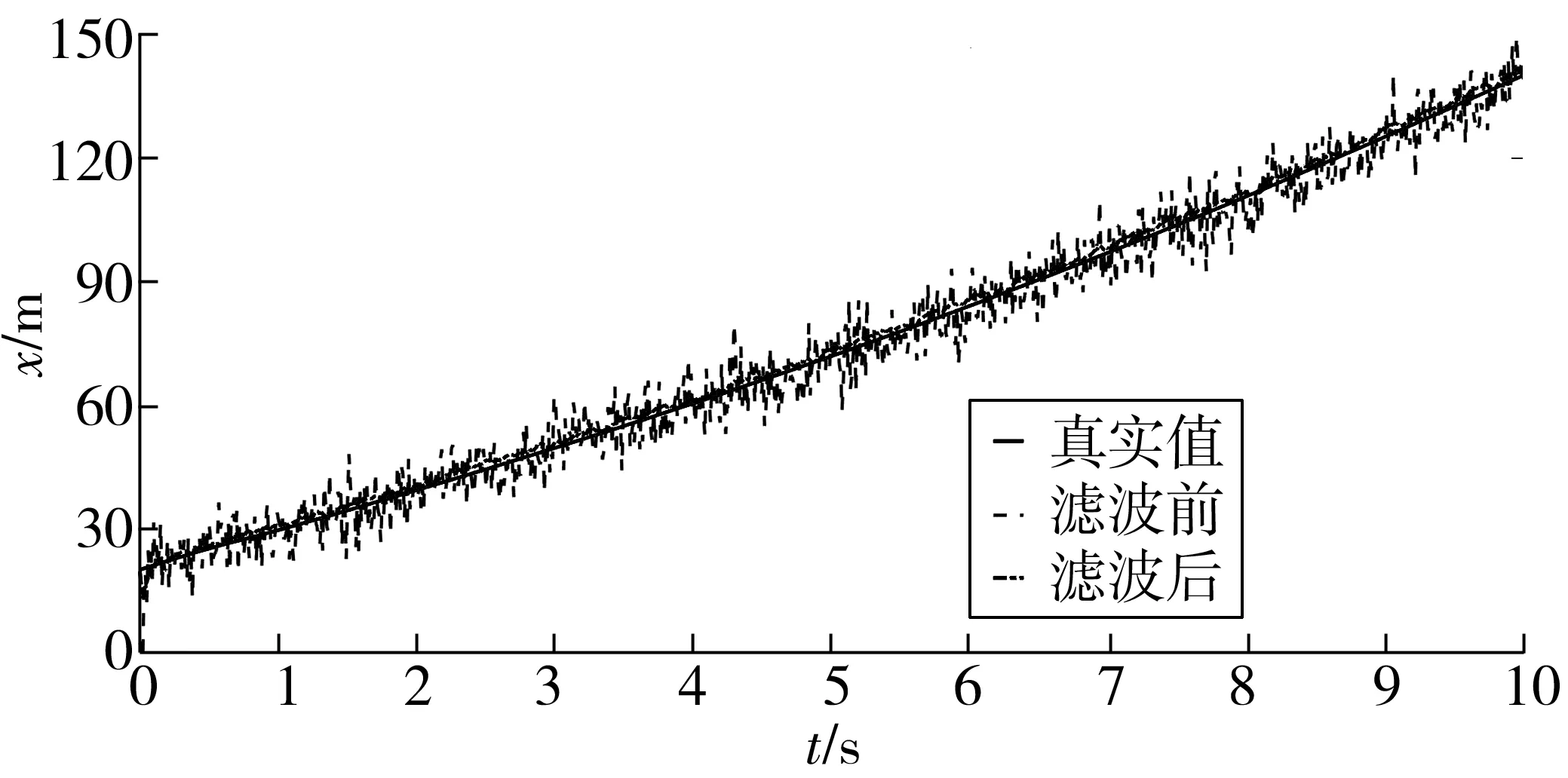
图4 改进卡尔曼滤波后车辆行驶横向位移变化曲线Fig. 4 Variation curve of vehicle lateral displacement after improved Kalman filtering

采用均方误差(mean squared error，MSE)和均方根误差(root mean squared error, RMSE)对数据经过有无改进卡尔曼滤波后的精度进行评价。

(26)

(27)

通过式(26)、式(27)计算的数据结果如表2。

采用MSE和RMSE评价数据精度是否有提高，通过对比有无改进卡尔曼滤波处理测量值，其相对应的提高值如表2。由表2可知，改进卡尔曼滤波算法使车辆行驶数据更加精确，更接近理想值。

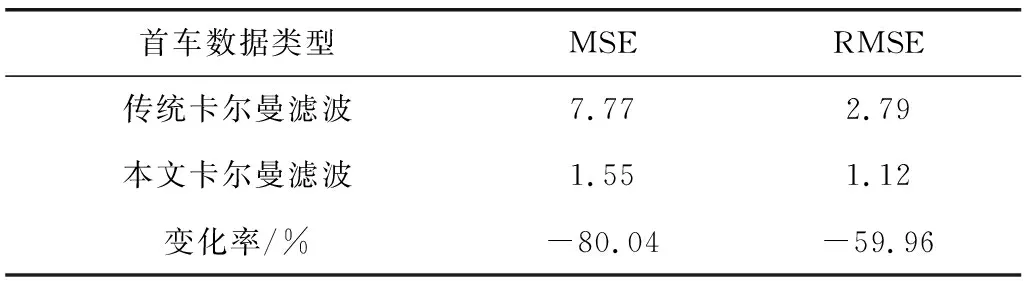
表2 有无改进卡尔曼滤波算法数值分析Table 2 Numerical analysis of improved Kalman filtering algorithm

将滤波后的数据带入CACC车辆行驶轨迹预测算法中，通过对比CACC车辆的加速度、速度变化，分析有无改进卡尔曼滤波对车辆行驶状态的影响。图5反映了车辆在行驶过程中不同滤波方法处理后的数据带入CACC车辆中加速度的变化。

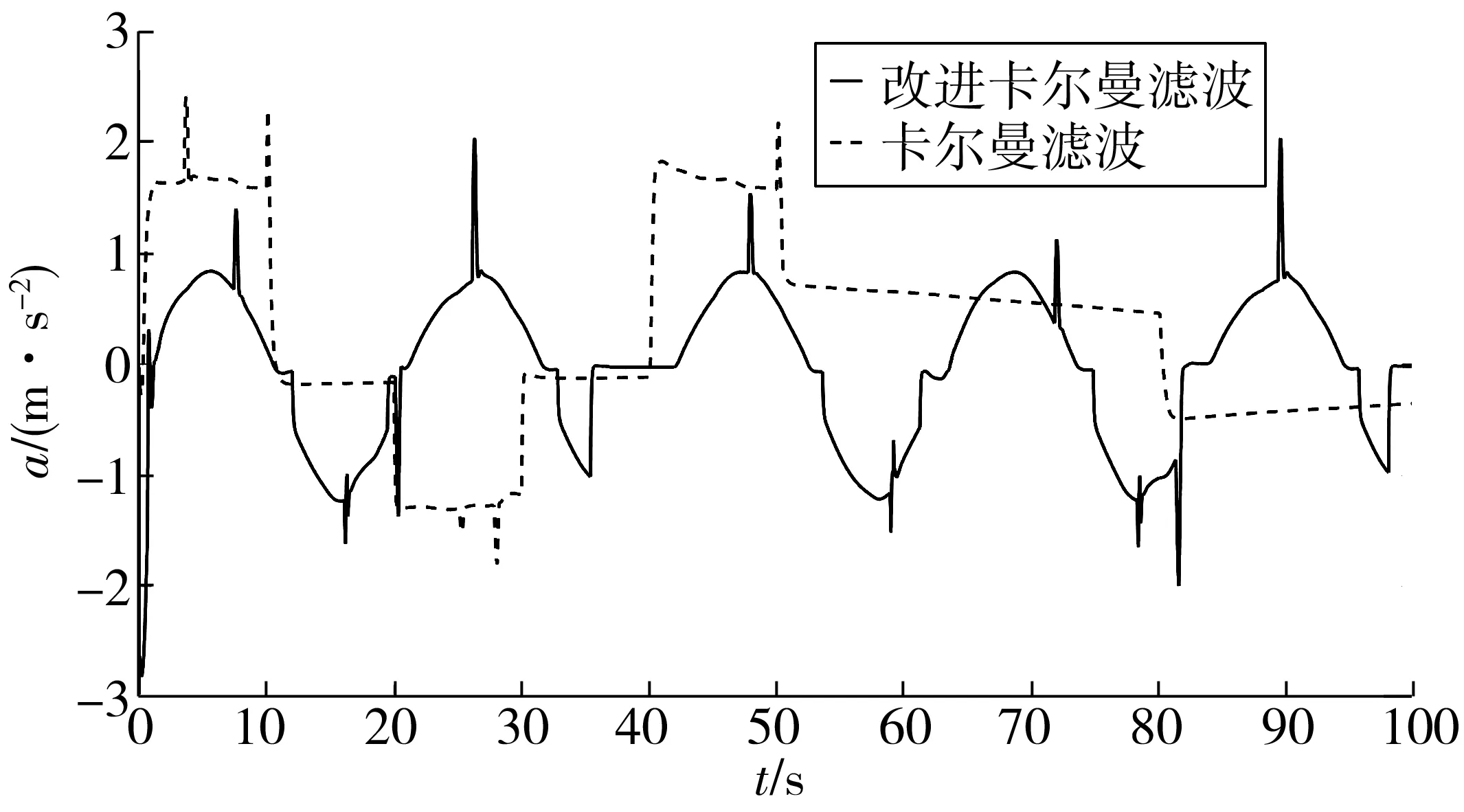
图5 车辆加速度对比曲线Fig. 5 Comparison curve of vehicle acceleration

通过表1中设置的加速度参数可知，改进后的卡尔曼滤波更符合正弦曲线的变化，而卡尔曼滤波后的加速度变化在某一时间点趋于稳定，没有产生较大的波动，故对应的速度为均加/减速行驶。通过对比分析车辆加速度数值变化可知，未经改进卡尔曼滤波算法处理数据带入系统后其加速度波动较大，经过改进卡尔曼滤波算法处理后的数据带入系统后其加速度较稳定，其车辆加速度主要在-2～2 m/s2内变化，保证了驾驶员和乘客的舒适性。

图6为车辆速度对比曲线。

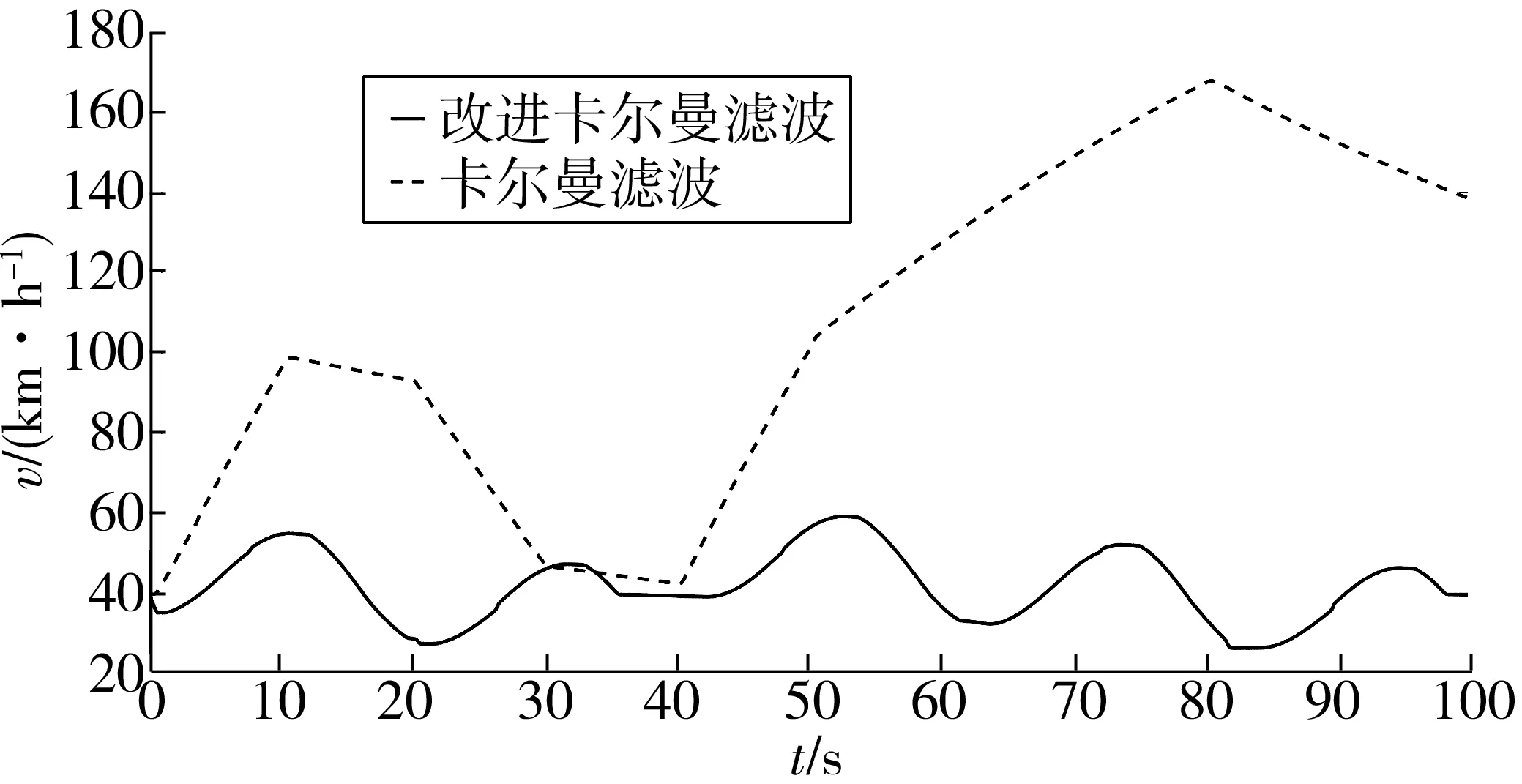
图6 车辆速度对比曲线Fig. 6 Comparison curve of vehicle speed

根据微积分定理，加速度是速度对时间的一阶导数，所以图6和图5的变化趋势一致，即速度变化曲线(图6)与加速度变化曲线(图5)相对应。在 40 s 后两种速度大小差距越来越大，两种方法处理的数据带入CACC系统中的速度变化如此大，其原因如下：首先，图5中经卡尔曼滤波后的加速度几乎为定值变化，而经改进卡尔曼滤波后的加速度几乎在区间内进行波动且变化规律符合设定的加速度变化曲线；其次，车辆在弯道行驶过程中速度方位角在不断变化，间接证明笔者建立的基于速度方位角的改进卡尔曼滤波算法对弯道行驶的车辆有效；最后，由图6可知，车辆行驶速度通过卡尔曼滤波处理后，其波动范围较大且车辆速度在不断增加，究其原因可能车辆响应存在噪音，产生误差，车车之间的通讯延迟、道路崎岖变化也是极有可能造成较大范围的波动。改进后的卡尔曼滤波速度变化较平稳，同加速度变化曲线较一致，具有规律性和较好的稳定性、舒适性。

经过仿真实验分析，改进卡尔曼滤波算法使车辆行驶具有较好的稳定性，提高驾乘人员的舒适性。改进卡尔曼滤波算法处理后的数据其位移更接近真实值，使数据更加准确；其加速度和速度浮动范围相比改进前卡尔曼滤波算法较小，从而说明了改进卡尔曼滤波后数据应用到车辆行驶过程中在同等时间内速度变化波动较小，保证了车辆在弯道行驶的平稳性，更有利于驾驶人和乘客乘坐舒适性。

4 结 语

通过研究CACC车辆在弯道行驶过程中传感器获取车辆信息存在噪声对车辆行驶产生误差的问题，利用改进卡尔曼滤波算法对传感器获取的数据进行处理，并使用CarSim和Simulink对该算法进行仿真，在仿真过程中将有无改进卡尔曼滤波算法对车辆行驶状态的影响进行对比。仿真结果表明，经改进卡尔曼滤波处理后的数据具有更高的精度和驾乘人员舒适性，更接近于车辆在弯道行驶的真实情况。研究结果为车辆在弯道行驶过程中提供一种数据处理方法和参考依据。

接下来研究如何将该算法应用于实车和分析该数据在实车验证过程中出现的情况，同时研究CACC车队在弯道行驶过程中如何保持巡航等情况和基于CACC数据精度的车辆模型预测控制轨迹在不同工况下的行驶状态。