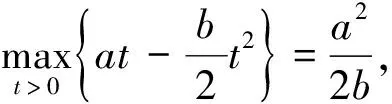一类带p(x)-双调和算子的Kirchhoff型方程解的存在性①

余颖，储昌木，何忠菊

贵州民族大学 数据科学与信息工程学院， 贵阳550025

设Ω⊂RN(N≥3)是具有光滑边界∂Ω的有界域，考虑一类带p(x)-双调和算子的Kirchhoff型方程

(1)

近年来，涉及p(x)-拉普拉斯算子的椭圆方程及变分方法的研究， 受到了许多学者的关注[1-8].特别地，文献[1]研究了涉及凹凸非线性项的p(x)-双调和方程

(2)

针对q(x)，r(x)和p(x)满足不同的条件，分别应用强制弱下半连续性、Ekeland’s变分原理及山路引理等变分方法获得了方程(2)非平凡弱解的存在性. 然而，关于带p(x)-双调和算子的Kirchhoff型方程的研究结果相对较少[9-11].受以上文献的启发，本文讨论方程(1)非平凡弱解的存在性.

(3)

则方程(1)至少有一个非平凡弱解.

1 预备知识

令

Lp(x)对应的范数为

Wk，p(x)(Ω)={u∈Lp(x)(Ω)：Dγu∈Lp(x)(Ω)，|γ|≤k}k=1，2，…

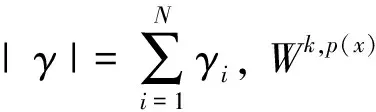
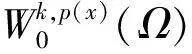
其范数为

‖u‖X=‖u‖1，p(x)+‖u‖2，p(x)

令

由文献[12]知，在X中‖‖与‖‖X等价，X是可分的自反Banach空间.

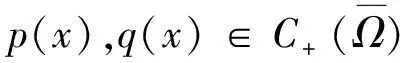
若‖u‖≤1，则有‖u‖p+≤ρ(u)≤‖u‖p-； ‖u‖=0当且当ρ(u)=0.

且满足：

(i)ψ′(u)是连续且有界的严格单调算子；

(iii)ψ′(u)是同胚的.

定义1如果对任意的v∈X， 有

则称u∈X为方程(1)的弱解.显然，方程(1)的弱解与泛函

的临界点等价.

2 主要结果的证明

在证明主要结果前，先证明泛函J满足(PS)c条件.

证设{un}⊂X为J的(PS)c序列，即

J(un)→cn→∞

(4)

且在X*中J′(un)→0(n→∞). 其中X*是X的对偶空间.

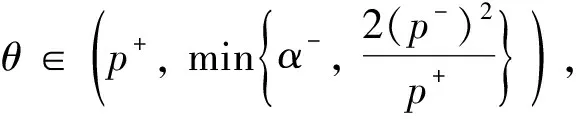
(5)

由p->1知， {un}在X中有界.

接下来证明在X中un→u.由于X是自反Banach空间，且{un}在X中有界，所以存在子列(仍用{un}表示)和u∈X，使得当n→∞时，

(6)

由(6)式和Hölder不等式可知，当n→∞时，

(7)

类似地，当n→∞时，

因此

(8)

由(4)式可知， 〈J′(un)，un-u〉→0， 即

综上所述， 可得

(9)

因为{un}在X中有界，所以存在子列(仍用{un}表示)和u∈X，使得当n→∞时，

由(6)式和Hölder不等式，对任意v∈X， 有

(10)

因为

且当n→∞时，〈J′(un)，v〉→0，故

因此

根据变分法基本原理[16]可得

f(x)|u(x)|α(x)-2u(x)-g(x)|u(x)|β(x)-2u(x)=0 a.e.x∈Ω

又因为f(x)，g(x)>0，所以u=0.因此

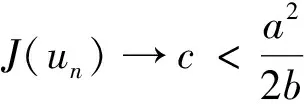
(11)

由(9)式可得

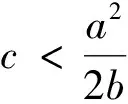
下面验证泛函J满足山路引理.

引理2当定理1的条件成立时，泛函J具有如下山路几何结构：

(i) 存在ρ，δ>0，使得对任意u∈X且‖u‖=ρ，有J(u)≥δ>0；

(ii) 存在w∈X满足‖w‖>ρ且J(w)<0.

证由紧嵌入XLα(x)(Ω)知，存在C>0，使得|u|α(x)≤C‖u‖.

设‖u‖=ρ<1，则

注意到p+<2p-且p+<α-，故存在ρ，δ>0，使得对任意u∈X且‖u‖=ρ，有J(u)≥δ>0.

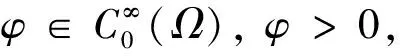
由(3)式可得，当t→+∞时，有J(tφ)→-∞.则当t>1足够大时，令w=tφ， 使得‖w‖>ρ且J(w)<0.

定理1的证明由引理2知，J具有山路几何结构.定义

Γ={ξ∈C([0， 1]，X)：ξ(0)=0，ξ(1)=w}