一种基于节点影响力的重叠社区发现算法

姚 越，程晓辉

（北京劳动保障职业学院，北京 100029）

复杂网络是复杂系统的高度抽象，可以用节点和边构建的图模型表示，其中社区结构性表达的是网络中节点的聚合群体特性，该特性的挖掘即社区发现[1]是通过节点与邻居节点间的紧密联系程度进行社区聚类，同一社区彼此紧密连接而不同社区节点联系相对较弱[2]。社区发现对理解复杂网络系统的功能和组织至关重要[3]。

经典的重叠社区发现算法是Gregory[4]提出的COPRA 算法，该算法是一个多标签传播算法，操作简单且执行较高效，但在更新标签中存在传播随机性和结果鲁棒性差的问题。Ma 等[5]在COPRA 的基础上提出了COPRAPC 算法，该算法通过聚类系数限制每个节点拥有的标签数量。张静宜[6]提出了基于节点PR 值和优化Jaccard 相似性指标的DSLPA，改善了SLPA 标签传播随机性的问题。王林等[7]提出以LeaderRank 重要性排序算法作为SLPA 算法节点标签更新顺序的依据，获得了更稳定的重叠社区生成结果。郭峰等[8]以DOCNet 算法框架，在初始节点选取和节点隶属度计算2 个方面寻求改进，提出了改进的重叠社区发现算法DOCLLE。陈晶等[9]提出基于COPRA 改进的OCKELP多标签传播算法，融合k-shell 解决了COPRA 选择初始节点随机性的问题。贾慧娟等[10]提出的COPRA-S 算法，以边缘节点为中心的桥梁节点群内进行标签传播，以此提升发现重叠社区的速度。不同研究者针对标签传播的随机性进行改进，但在标签传播中均没有充分考虑节点的属性信息及节点间关联影响，对于COPRA随机性和鲁棒性的改进仍是一个开放性问题，本文提出了一种基于节点影响力的标签传播算法NI-COPRA（Node Influence based-Community Overlap Propagation Algorithm），通过对节点重要性的量化解决标签传播过程中选择初始节点的随机性，利用节点影响力的度量改善标签传播过程中选取邻居节点标签的随机性，以挖掘更加稳定的重叠社区。

1 相关知识

1.1 COPRA 算法

COPRA 算法是较经典的多标签传播算法，COPRA中定义每个节点最多属于v 个社区，每个标签隶属系数为b（c，u）表示节点u 从属社区c 的强度，每个节点可以有多个标签。算法初始，节点用自身标号作为标签，隶属系数为1，随机选取1 个初始节点，在邻居节点间进行标签传播和更新，在标签更新的过程中，通过设置v 值筛选出隶属系数大于1/v 的标签，通过多次迭代发现重叠社区。隶属系数的计算方式如式（1）所示

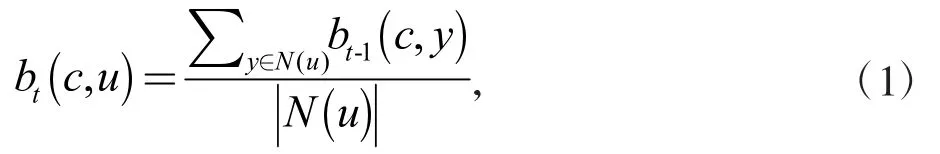
式中：N（u）为节点u 的邻居节点集合；bt-1（c，y）为上次迭代节点u 的邻居节点标签信息。

1.2 网络嵌入学习

网络嵌入是用低维的连续特征表示网络原有的高维离散特征，其目的是为获取网络结构数据之间的相似性并改善稀疏性。近年来，众多网络嵌入方法应用于社区发现，并取得了一定研究成果。如DeepWalk[11]首次采用自然语言处理中的模型与社交网络领域的网络结构结合，较贴切地表示了网络拓扑结构。Node2vec模型[12]改进了DeepWalk 节点游走的方式，将广度优先遍历和深度优先遍历引入到随机游走中，较好地反映了网络真实结构，且具有较高的灵活性和普适性。Line[13]考虑了节点1 阶和2 阶相似性，实验结果表明，该模型适用于规模较大网络中可应对传统梯度下降方法的限制。文献[12]中实验结果显示，在多标签分类任务上，Node2vec 取得了比Deepwalk 和LINE 算法较好的划分效果。本文采用Node2vec 模型遍历网络结构并生成节点序列，通过Skip-gram 模型训练目标节点序列得到节点的低维向量表示。

2 NI-COPRA 算法设计

COPRA 算法在初始节点的选择及标签传播时存在随机性的问题，本文所提NI-COPRA 算法，首先采用基于信息熵的节点重要性排序算法确定节点更新顺序，其次在融合节点重要性与节点相似性的基础上，提出1 种计算节点影响力的方法定义隶属系数进行标签传播，以发现准确稳定的重叠社区。

2.1 融合重要性与相似性的节点影响力

本文提出NI-COPRA 算法中节点通过邻居节点的综合影响力选择标签，节点影响力是将节点重要性与相似性进行融合，应用在隶属系数中进行标签传播，获得更准确稳定的重叠社区。

2.1.1 节点重要性度量

现有研究中具有众多的节点重要性度量方法，例如节点度、中心度、介数中心性及vote 算法等。信息熵[14]以特定信息的出现概率量化来间接表达信息的价值，文献[14]以信息熵的角度度量复杂网络中的关键节点识别，不仅在信息属性的准确度量有很好的效果且在计算性能与其他一些经典排序算法相比，获得了较好性能。本文提出了基于信息熵的EnRenew[15]重要性算法，从局部范围开始最终获得网络的重要性排序，在选取了初始最大信息熵的节点之后，通过多阶步长的邻居节点迭代削弱传播能力获得最终网络的节点排序。相比于传统排序算法仅用节点1 阶信息，节点的熵可以衡量节点的多阶局部信息，从而使得后续迭代选取关键节点更加有效。受到文献[13]的启发，本文提出的算法使用2 阶步长迭代。节点初始重要性公式如式（2）所示

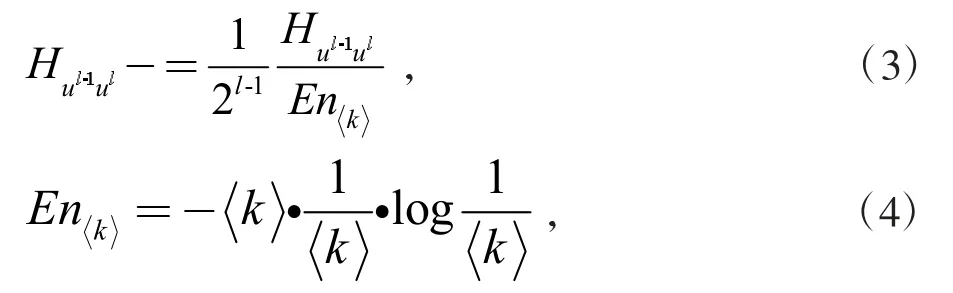
式中：ul为节点ν 通过l 步长达到的节点集合，例如ul是节点ν 的一阶邻居集合；k 为网络中平均度，当k 为整数时，En＜k＞可以看作是k 正则图中任意一个节点的信息熵。

2.1.2 节点相似性度量

本文中对于节点相似性的量化是通过节点嵌入学习而获得的。首先，基于Node2vec 模型遍历网络拓扑结构生成节点序列，通过Skip-gram 训练目标节点序列得到节点低维向量表示，最后利用余弦相似度计算节点间的相似值。

Node2vec 模型中提出1 种有偏的随机游走算法，可同时满足节点之间的同质性与结构相似性。给定一个源节点μ，假设随机游走的步长为固定长度L，从源节点μ 开始，使用式（5）生成邻居序列

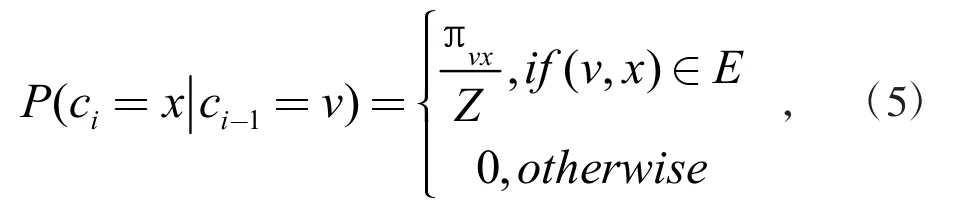
式中：ci为随机游走中的第i 个节点；Z 为归一化因子，πνx为节点ν 到节点x 转移概率；πνx=αpq（t，x）·ωνx，α 为p、q 参数确定的带偏置搜索算子。具体游走过程如图1所示，p 控制访问ν 后返回t 的概率，q 控制图中未发现部分的概率。当p＞max（q，l）时，采样不会回溯；当p＜max（q，l）时，采样会更倾向于返回上1 个节点。当q＜1 时，采样会倾向遍历远离t 的节点，即深度优先遍历；当q＞1时，采样会倾向遍历周围的节点，即广度优先遍历。

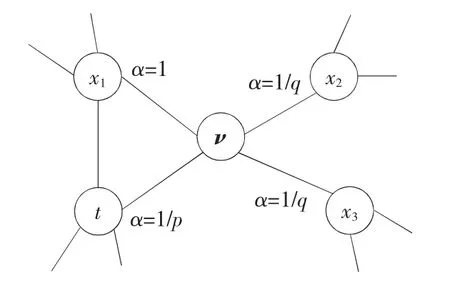
图1 随机游走过程示意图

Skip-gram 是一种语言模型，该模型能够极大化单词出现在上下文中的概率。其是使用1 个单词来预测句子。模型优化目标函数如式（6）所示

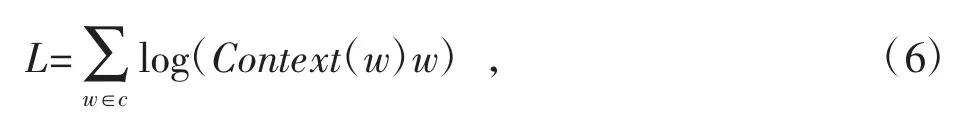
式中：w 为当前词；c 为类似自然语言的语料库；Context（w）为词的上下文。在本文中，该语料库为网络中节点随机游走后产生的线性序列。

该模型是由输入层、隐含层和输出层组成。输入层和隐含层之间的权重矩阵为W1，隐含层和输出层之间的权重矩阵为W2。如式（7）所示

通过Skip-gram 嵌入得到节点的特征向量，用余弦相似度计算作为节点间相似性的度量标准，节点相似性公式如式（8）所示

2.1.3 节点影响力计算

标签传播过程中，NI-COPRA 算法充分考虑节点自身，及其邻居节点在网络中的不同重要性与动态相关性，结合节点重要性与节点间相似性度量量化邻居节点的综合影响力，进一步应用在隶属系数计算中使得节点标签的更新更为合理。邻居节点v 对节点u 的影响力定义如式（9）所示

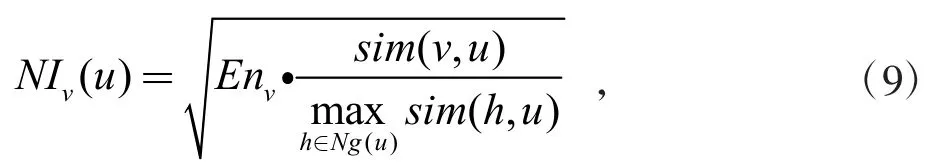
式中：Ng（u）为节点u 的邻居节点集合。

2.2 基于节点影响力的NI-COPRA 算法

2.2.1 算法节点更新策略

（1）在标签传播过程中，节点接收到来自邻居节点的主标签组成标签集合，es（c，b）表示为c 社区，b 为隶属系数

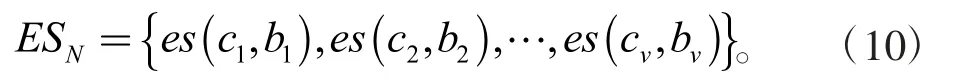
（2）标签传播过程中考虑邻居节点的影响力，计算更新标签后节点u 对社区c 的隶属系数

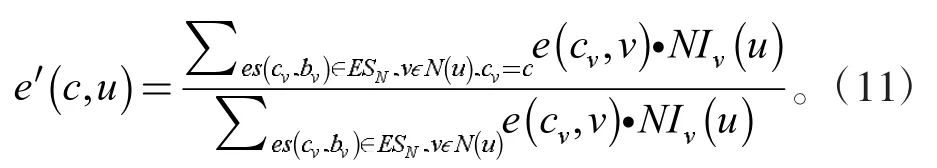
（3）对剩余标签的归属系数进行归一化

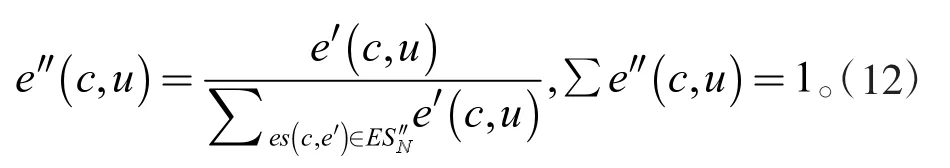
2.2.2 基于节点影响力的重叠社区NI-COPRA 算法实现

NI-COPRA 算法的具体算法步骤如下所述。

（1）节点重要性和影响力计算。初始化时将网络中每个节点主标签设置为节点ID 号，隶属系数均设置为1。利用节点重要性得到每个节点信息熵S 并按升序排列得到序列E，通过Node2vec 模型生成节点序列，然后使用Skip-gram 训练得到节点特征向量，利用余弦相似度公式（8）得到节点间的相似性值。利用式（9）计算网络拓扑结构中的每个节点与邻居节点的节点影响力值。

（2）标签传播。节点u 邻居节点将主标签（隶属系数最大的标签）传递给节点u，主标签形成集合ES。利用式（11）更新标签隶属系数形成标签集合，删除隶属系数小于，形成新的标签集合。利用式（12）归一化生成新的标签集合ESu，该集合中隶属系数最大的标签作为主标签Lu。

2 实验结果与分析

为了验证本文提出的NI-COPRA 算法的有效性，与COPRA 算法、LPANNI 算法[16]进行对比。本文实验所有算法均采用Python3 实现，基本配置CPU 为Intel（R）Core（TM）I7-8700 CPU @ 3.20 GHz，内存为32 GB。

2.1 评价指标

2.1.1 标准互信息NMI

NMI 函数的取值为[0，1]，其取值越大表示与标准结果越接近，NMI 评价指标如式（13）所示：

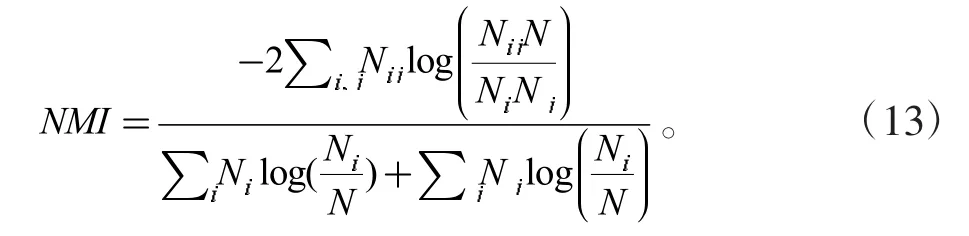
2.1.2 扩展模块度EQ

使用扩展模块度（EQ）[17]作为重叠社区的评价指标。其公式如式（14）所示

式中：m 为网络中连边总数；Qi、Qj为节点νi、νj所属的社区个数，Aij为网络邻接矩阵中的元素；ki、kj分别为节点νi、νj的度；Cy为第y 个社区包含的节点集合。EQ函数的取值为[0，1]，其取值越大，表示社区划分的结果越有效。

2.2 实验数据集

2.2.1 真实网络数据集。

本文采用6 个真实网络数据集，其中3 个小规模数据集，分别是cora 引文网络数据集、wiki 数据集及CA-GrQc 科学合作网络数据集，另外包括3 个中等规模数据集，分别是优良保密协议网络PGP 数据集、condmat 科学论文作者的协作网络数据集及cit-hepph高能物理现象引文网络数据集。表1展示了数据集的具体信息。

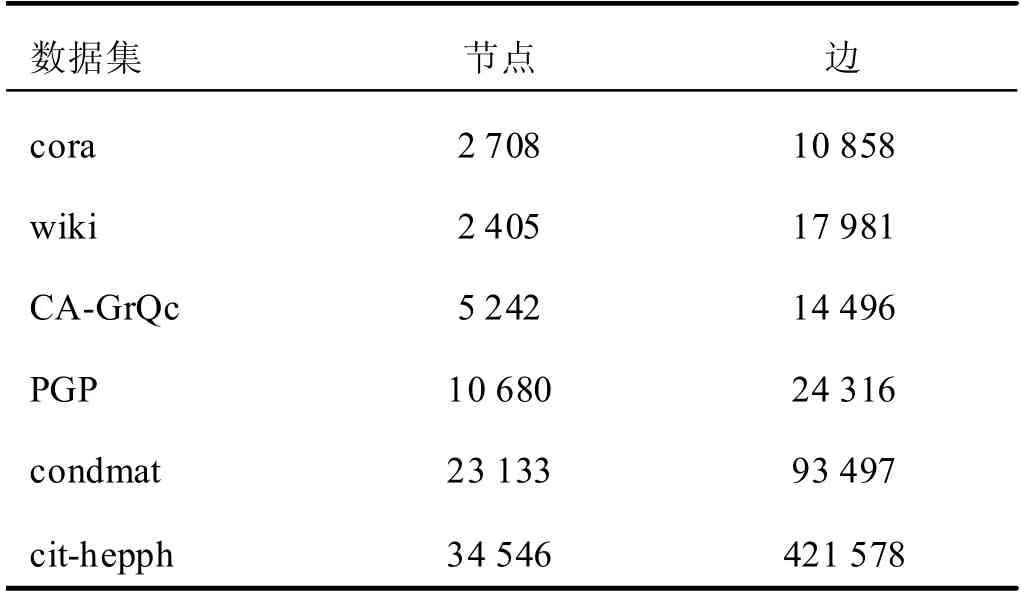
表1 真实网络数据集

2.2.2 人工生成网络数据集。

本文使用LFR 基准发生器生成参数指定分布的人工生成网络，om 代表重叠节点所属社区个数，om 从2 到8 生成了7 个不同的网络数据集，LFR 基准网络中参数的具体信息见表2。

表2 LFR 基准网络数据集

2.3 实验过程与结果分析

本文实验验证了节点重要性排序算法与社区发现效果，其中节点重要性是通过SIR 模型进行传播实验对比，社区发现有效性是通过EQ 模块度评价指标及NMI 标准化互信息指标进行验证。

2.3.1 重要性算法验证

本文采用SIR 模型验证排序算法，选择初始感染节点拟合病毒的传播过程，一段时间后感染节点的规模衡量初始感染节点传播影响力。图2是本文所提的重要性算法与degree 算法、vote 算法及k-shell 算法进行传播实验对比。

图2 各算法在不同时间t 下的F（t）变化情况

在相同传播时间t 下，先到达稳定状态且F（t）值较大表明网络中的影响规模越大，传播速度越快。

2.3.2 社区发现准确性验证

（1）模块度EQ 实验结果分析。为了验证本文NI-COPRA 算法社区划分结果的有效性，该算法将COPRA 算法及LPANNI 算法作为对比实验，重叠社区发现结果用EQ 指标进行评价。出于对实验效果与有效性的考虑，参数p 和q 分别取0.25 和4，Skip-gram 模型随机游走序列长度设置为80，窗口大小设置为5，向量维度设置为128，最大迭代次数T 设置为100，COPRA 算法中参数V 取值2～10，在每个数据集上均取最佳参数值，COPRA 算法运行10 次取平均EQ 值，LPANNI 算法及本文算法是稳定的社区发现算法取运行一次的EQ 值。实验结果见表3。

表3 真实网络数据集重叠模块度EQ 值比较

表3展示了各算法在6 个真实网络数据集上EQ值。NI-COPRA 划分的重叠社区模块化度量值EQ 是明显高于COPRA 算法和LPANNI 算法的。本文算法在小规模数据集和中等规模数据集上，都发挥了很好的优势。

（2）NMI 实验结果分析。在人工生成网络G 上，将对比实验COPRA 算法在7 个数据集上取平均NMI 值，LPANNI 算法和本文NI-COPRA 稳定算法取1 次运行的NMI 值，最终NMI 的评价对比结果如图3所示。

图3展示了各算法在人工生成网络7 个数据集上NMI 值。由图3可知，对于具有复杂重叠社区的网络，NI-COPRA 在复杂重叠社区发现中表现优良，准确性和稳定性都比之前的标签传播算法有了很大改进。

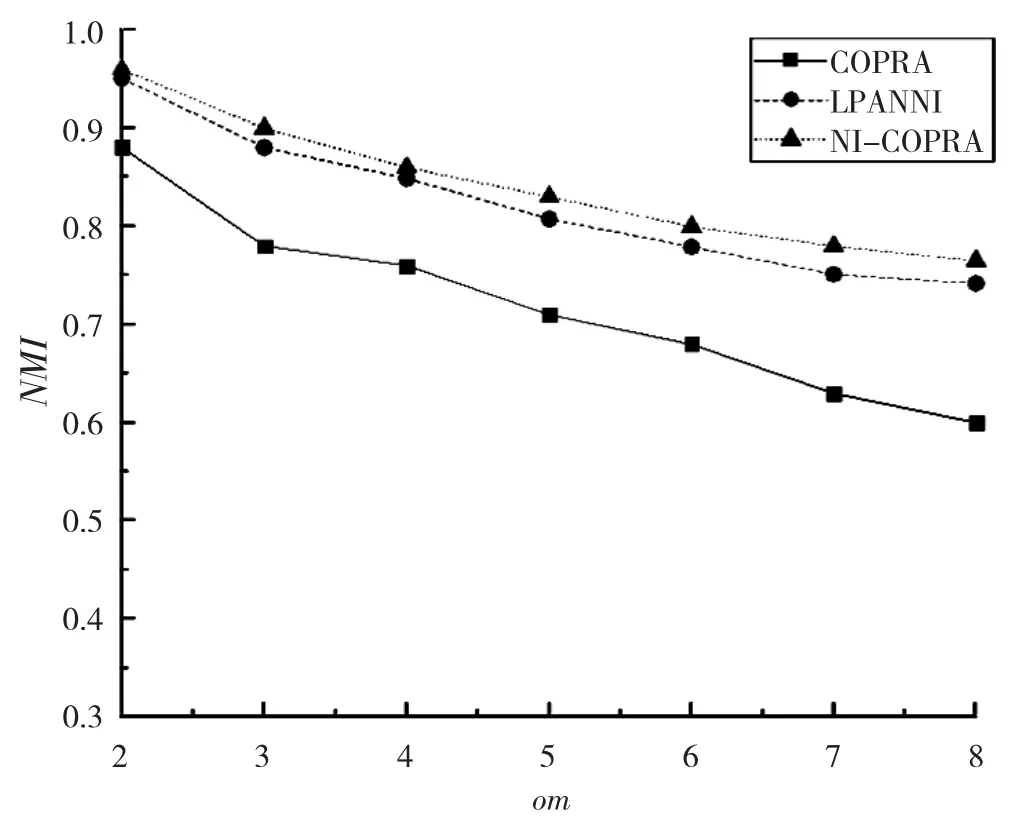
图3 人工生成网络不同om 精度下NMI 值对比

4 结束语

本文在COPRA 算法基础上，主要针对其标签传播过程中存在随机性及发现重叠社区稳定性差的问题，提出了1 种基于节点影响力的重叠社区发现算法NI-COPRA。首先，通过信息熵量化节点的个体价值，进行重要性度量以确定节点标签更新顺序；其次，引入节点影响力进行标签选择，利用节点重要性与相似性融合确定影响力，更新社区隶属系数并进行标签传播，在迭代更新中，以稳定的节点标签确定归属的社区。在真实网络和人工生成网络上验证了本文算法的有效性。在今后将进一步优化算法，引入到有向加权网络中及动态重叠网络中，满足如今更多的复杂网络结构需要。