核设施退役数字仿真中人员行走最优路径研究

古 强，寇骄子，李文涛

（中核四川环保工程有限责任公司，四川 广元 628017）

全球已有140 多座核电反应堆永久关闭，开始或等待退役。在运行的反应堆中，有部分也已超出设计寿期。除核电反应堆外，一些国家还有大量的遗留军用核设施需要退役，这些工作均面临不同程度的难题和挑战，尤其是在退役策略选择、辐射安全和成本预算方面存在很大的不确定性，需要大量的准备工作，以达到方案最优化。

消除这种不确定性的有效方法之一是利用仿真技术。利用仿真技术可为退役策略和方案的选定、操作顺序的优化、退役废物数量的估算和形状的判断、辐射剂量的估计以及退役操作前人员的培训等多项工作提供有效的支持，使整个退役过程从放射性废物产生到成本尽量低等多个方面真正符合合理可行原则。

近年来，我国对于核设施退役监管要求越来越严。同时，加大了核设施退役投入，并在部分退役技术方面取得了一定的突破。但在具体的退役实践经验还较为欠缺，对于在退役活动中操作人员的安全和健康的保障具体措施的研究应用还较少。因此，本课题是对核设施数字化仿真中人员行走的最优路径进行研究，基于推导计算出的辐射场分布，按照在相同工作时间，人体受照剂量的累计值最低，采用A-Star 算法进行两点间最优路径的计算，将最优路径转换为数字化仿真模型中的寻路模型进行呈现，这是在核设施数字化仿真退役中一次重要的尝试，将为核设施真实退役提供重要参考。

1 基本理论模型

图论研究中的一个经典算法是最短路径算法，即在图中找到2 个结点之间最短的路径。

计算最短路径的算法即“最短路径算法”。常用最短路径算法包括：迪杰斯特拉算法，即Dijkstra 算法；SPFA 算法Bellman-Ford 算法，即队列优化算法；弗洛伊德算法（Floyd）Floyd-Warshall 算法；Johnson 算法；A-Star 算法。

本项目主要采用A-Star 算法进行研究。该算法是基于启发式搜索，即在状态空间中对每个搜索的位置进行评估，以确定最好的位置，再从这个位置搜索直至到达目标。这样省略了搜索大量没有作用的路径，使得效率得到了提升。在启发式搜索中，位置的估价是极其重要的方面，不同的估价可能到达不同的效果，其缺点是在长路径上的速度呈现几何级数地提升。

2 项目数据源

本项研究以待退役核设施为原型，采用3dMax、Unity 等三维仿真工具和平台，对待退役核设施的主要建筑、设备、管线等进行了三维模型构建。同时，利用蒙特卡洛程序对辐射场进行计算，基于有限的辐射场数据，采用神经网络插值的方法重构了辐射场。采用虚拟现实技术的核辐射可视化方法，将辐射场与设施叠加，用以分析和处理辐射信息，解决实时对辐射场进行渲染呈现的问题，并以多种图形化的方式直观地显示核辐射剂量场的分布情况。

采用栅格路径对设施内部空间进行了分隔。栅格路径是搜索算法基于栅格地图得到的一个栅格序列（数组），是本项目研究在路径算法的实践之一。栅格法的使用与障碍物栅格的生成，进而将实际三维仿真地图转换为栅格地图，栅格路径无法直接应用于实际地图中，需要将其进行处理，将栅格路径转换为直角坐标系下的路径。在项目研究中，将核设施内部的空间按照标准的大小进行栅格绘制，形成了地理栅格内部空间结构，用于与辐射场进行耦合计算，采用A-Star 算法进行路径寻址，最终找到最优路径。

3 A-Star 启发式搜索在辐射场寻址中的应用

3.1 A-Star 启发式搜索研究

设从A 点移动到B 点，但是这两点之间被一堵墙（不可走区域）隔开，首先把搜索区域简化为了二维数组，数组的每一项代表一个格子栅格被定义成2 个状态，即可走（walkable）和不可走（unwalkable）。通过计算出从A 到B 需要走过哪些节点，就找到了路径。一旦路径找到了，便可以从一个节点的中心移动到另一个节点的中心，直至到达目的地。

A-Star 算法核心公式就是F 值的计算

F=G+H，

式中：F 为总移动代价；G 为开始点到当前节点的移动代价；H 为当前节点到结束点的预估移动代价。

3.1.1 G 值的计算

假设当前A 节点，邻近有8 个格子可走（上、下、左、右、右上、右下、左上、左下），当往上、下、左、右这4个格子走时，移动代价为10；当往左上、左下、右上、右下这4 个格子走时，移动代价为14。（等腰直角三角形勾股定理：斜边2=2×直角边2）。

基本公式为

G=移动代价。

根据环境应用的需要，G 值的计算可以进行拓展。如加上栅格不同辐射场量因素对寻路的影响，可以给不同栅格赋予不同代价因子，来体现出G 值的差异。由于辐射场估算已经给每一个栅格赋予了辐射场值，可以利用该数值转换为代价因子，在移动代价相同情况下，低场量的G 值更低，算法就会倾向选择G 值更小的低场量栅格。

拓展公式为

G=移动代价×代价因子。

3.1.2 H 值的计算

19世纪，赫尔曼·闵可夫斯基创造了曼哈顿距离（Manhattan Distance）一词，其是一种几何用语。在几何度量空间里，用于标明在标准坐标系上2 个点的绝对轴距的总和，即两点在南北方向上的距离加上在东西方向上的距离之和。

二维平面两点a（x1，y1）与b（x2，y2）间的曼哈顿距离为

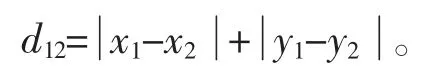
n 维空间点a（x11，x12，…x1n）与b（x21，x22…x2n）的曼哈顿距离为

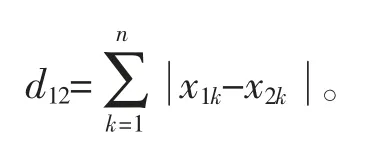
A-Star 算法之所以被认为是具有启发策略的算法，在于其可通过预估H 值，降低走弯路的可能性，更容易找到一条更短的路径。其他不具有启发策略的算法，没有做预估处理，只是穷举出所有可通行路径，然后从中挑选一条最短的路径。这也是A-Star 算法效率更高的原因。

3.1.3 开始搜索

开放列表（open list）用于记录所有可考虑选择的格子。

封闭列表（close list）用于记录所有不再考虑的格子。

（1）算法开始，首先搜索A 相邻的所有可能的移动位置，每个节点左上角的值G 表示该点到A 的距离，这里的H 就取其到B 的曼哈顿距离。最后，还要计算一个F 值，F=H+G。

（2）此时的起点A，将其加入由节点组成的开放列表之中，开放列表即是一个待检查的节点列表。

（3）查看与起点A 相邻的节点，把其中可走的（walkable）或可到达的（reachable）节点也加入到开放列表（open list）中。随后把A 从开放列表（open list）中移除，加入到封闭列表（close list）中，封闭列表（close list）中的每个节点都是现在不需要再关注的。

（4）从开放列表（open list）中选一个与起点A 相邻的节点，选择具有最小F 值的那个节点。

3.1.4 再次搜索

（1）接着把当前节点A1 从开放列表（open list）移到封闭列表（close list）中，搜索当前节点相邻的所有可能的移动位置，并且都加入到开放列表（open list）。

（2）把找到最小F 值的节点A2 从开放列表（open list）移到封闭列表（close list）中，然后检查与其相邻的节点。其右边的节点是墙壁（不可走unwalkable），进行忽略。左边的节点是父节点，在封闭列表（close list）中，也进行忽略。其他相邻的节点均在开放列表（open list）中，所以A2 节点寻路失败，选择开放列表（open list）中最小F 值的节点（列表中如果有多个最小F 值的情况，随机获取一个最小F 值节点进行下一次循环）。

（3）继续把找到最小F 值的节点A3 从开放列表（open list）移到封闭列表（close list）中，然后检查与其相邻的节点。按照如此循环直到移动到目标点B。最终过程结果如图1所示。

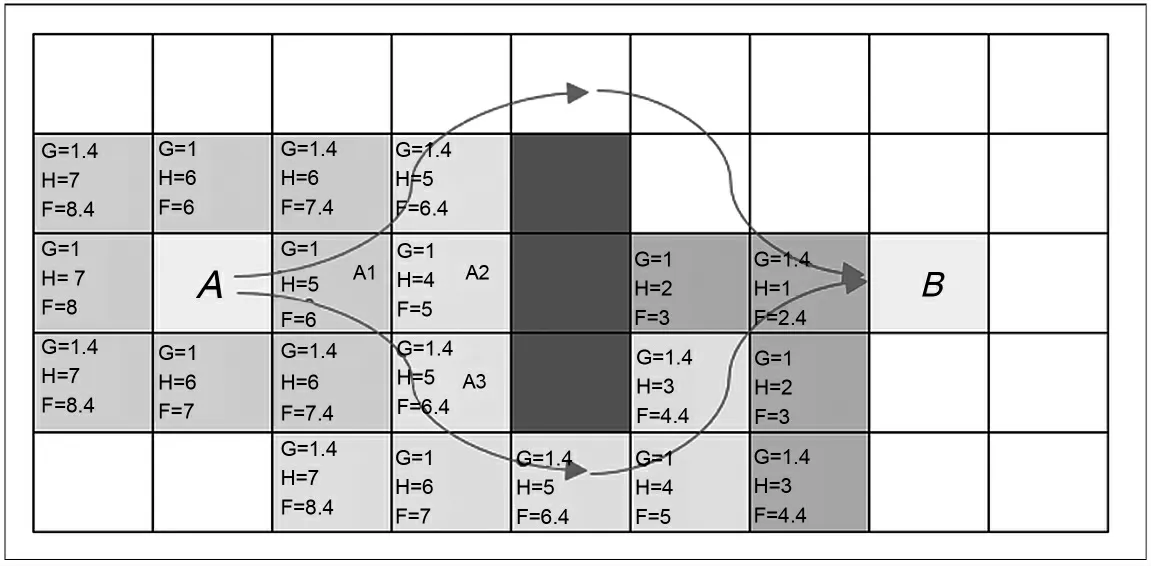
图1 路径搜索

3.1.5 补充

（1）最佳路线可能有多条，比如本文的示例，这取决于当开放列表（open list）存在多个F 值最小的节点时，先选取哪一个进行搜索。

（2）曼哈顿距离只是估算H 值最简单的一种方法，常用的方法还有欧几里德距离、切比雪夫距离等。

（3）实际应用中，为提高效率，还可以进行双向搜索。从起点和终点分别发起搜索，一方搜索到另一方的已检查节点时，即找到最佳路线。地图较复杂时，双向搜索可以显著减少寻路过程中检查的节点数量。

3.1.6 辐射场与代价因子

前文提到的“G=移动代价×代价因子”，如何将当前栅格辐射场量转化为合理的代价因子是核退役数字化仿真中人员行走路径最优化研究项目中的应用特殊性。

在理论上，通过源项调查获取的辐射场数值范围不常在一个数量级单位波动，需要使其数据标准化，将其限定在需要的一定的范围之内。将数据进行标准化就是将数据按照一定的比例进行缩放，让数据落入小范围的特定区间内。采用比较和评价进行指标处理时会经常用到，让数据不再受单位的限制，而将其转化纯数字，这种纯数值是无量纲的，这样对不同单位或量级的数据指标就能够进行加权和比较。在分析数据之前，应将数据进行标准化，并分析标准化后的数据。数据标准化即将统计的数据指数化。数据无量纲处理和同趋化处理是数据标准化处理的两个方面。数据无量纲化处理主要用于解决数据的可比性问题。数据同趋化处理主要解决不同性质的数据问题，即对不同性质指标加总不能正确反映不同作用力的综合结果，首先应考虑改变逆指标数据的性质，使所有指标对测评方案的作用力同趋化，再加总以得到正确的结果。经过以上所述的标准化处理，将原始数据转换为无量纲化指标测评值，这样原始数据通过转换已经处于同一数量级别，再进行综合测评分析。

经常使用的方法包含如下几种。

（1）简单缩放。

（2）逐样本均值消减（也称为移除直流分量）。

（3）特征标准化（使数据集中所有特征都具有零均值和单位方差）。

其目的都是在于加快梯度下降求最优解的速度，有可能提高精度。

通常的方法：

（1）线性标准化，即min-max 标准化或离差标准化，就是对原始数据进行线性变换，最终结果值映射到[0，1]区间之间。采用以下函数进行转换

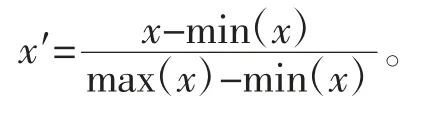
以上方法更适用于数值较为集中的情况。另外，这种方法也有明显的缺陷，即一旦max 和min 不稳定，结果很可能也不稳定，这将直接影响使用效果。

（2）Z-score 标准化，或者称为标准差归一化，这种方法将原始数据的均值（mean，μ）和标准差（standard deviation，σ）进行数据标准化。数据处理后符合标准的正态分布，即均值为0，标准差为1，转化函数为

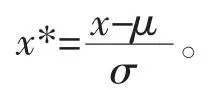
（3）非线性归一化，一般应用于数据分析较大的场景，采用数学函数将原始值进行映射。这经常使用到log、指数、正切等函数，最终将根据数据分布的具体情况决定非线性函数的曲线。

3.2 在辐射场寻址中的应用

采用虚拟现实技术对核设施退役过程中三维辐射场进行计算和评估，给定核设施退役作业过程场景，以此为基础构建目标问题动态三维辐射场模型，并对辐射剂量场采用蒙特卡洛数值模拟计算以及全范围的可视化呈现，既在人员的安全性上有足够的保障，又在经济性和可靠性上具有显著优势。

基于构建的核设施退役环境中的三维辐射场，进行核设施退役作业过程的建模并完成路线规划，如图2所示。

图2 辐射场中路线规划实现

基于虚拟仿真平台构建辐射场的三维仿真模型，将三维模型转化为基本的几何体，识别基本几何体的基本信息，为快速计算辐射场，利用蒙特卡洛程序进行核辐射场计算。利用有限的辐射场数据，采用神经网络插值的方法对辐射场进行重构，并采用虚拟现实技术实现核辐射可视化的方法，对辐射数据进行分析和处理，再将核设施与辐射场进行叠加，同时实现核辐射场实时渲染，进而以更直观高效的图形化方式呈现辐射剂量场的分布情况。

根据待退役核设施前期源项调查选取的4 000 个点位数据，选择其中2 000 个点的数据作为输入，在已知源项几何大小、活度、产生射线的种类和射线能量等基础信息上，利用蒙特卡洛程序及神经网络插值进行三维辐射场剂量分布情况进行可视化建模与分析。通过建立的算法进行仿真模拟，并用其余2 000 个点的数据对仿真结果和实际数据进行相对误差分析，不断调整算法模型参数，直到模拟辐射场与实际数字误差达到最小，最终确定辐射场模拟算法，实现了辐射场仿真分布误差小于30%的指标。

使用栅格法将核设施结构和辐射场离散化，进而对人员行走路径进行不断优化。在处于二维环境下时，建立了基于栅格的路径评估方法，用于评价路径选择的各种因素，并且基于图论算法设计了受到最小辐照的路径搜索方法，最终用于人员受照剂量最小的路径的选择。

在复杂的辐射环境下，采用组合优化的方法得到最小辐照路径的最优解。本次开发的人员行走路径优化方法和虚拟仿真技术相结合，不仅实现了核辐射场中人员行走路径仿真，还能够提供工作人员行走路径规划设计、优化、演练和评估等多种服务。

4 结束语

在核退役数字化仿真中研究人员行走最优路径，完成了辐射场量和A-Star 最优路径的耦合功能，并利用鼠标键盘等设备在核设施退役场景仿真系统动态交互起止点，可以满足核设施退役三维场景任意两点最优路径的计算。此项研究在核设施退役人员辐射防护方案设计中有重要的参考价值。