热环境中多孔功能梯度材料转动Timoshenko梁的自由振动特性分析

滕兆春 , 马铃权

(兰州理工大学 理学院, 甘肃 兰州 730050)

功能材料的概念最初是由美国贝尔研究所Morton博士在1965年提出,后经日本各研究所、大学及学会的大力提倡和重视,功能梯度材料(functionally graded material,FGM)的概念于1987年被新野正之、平井敏雄等日本学者提出.功能梯度材料是一种特殊的非均匀复合材料,通常由陶瓷和金属复合而成,其材料性质一般沿某一方向而连续变化.其中陶瓷材料具有较好的耐热性,而金属材料具有良好的机械强度,因此功能梯度材料可以在保持韧性的同时能减缓热应力以适应高温环境.功能梯度材料起初由日本方面用于火箭引擎和箭体的热防护材料,由于其较高的机械强度、独特的抗热冲击和耐热性能解决了由飞机高速飞行使机身形成极大内外温差而产生的热应力问题,引起很多国家宇航领域科技工作者的关注,功能梯度材料的研究迅速展开,国内外取得了显著的成果.目前功能梯度材料的应用非常广泛,如反应堆容器、聚变能源装置、生物医学部门、飞机、空间运载工具、国防工业和其他工程结构.随着各个领域对功能梯度材料结构的不断需求,人们对功能梯度材料及结构的力学行为进行了大量研究.早期研究成果详细可见Reddy、Li和Sina等[1-3]诸多学者的系列研究工作.近年来,Tang等[4]基于非局部应变梯度积分模型研究了功能梯度材料 Timoshenko梁的屈曲载荷和振动频率.Zhang[5]定义了功能梯度材料梁物理中面的表达式并考虑von Kármán应变-位移关系和高阶剪切变形理论,实现了功能梯度材料梁的拉弯解耦,应用Ritz法给出了功能梯度材料梁热过屈曲和非线性振动的近似解.Gupta等[6]基于非多项式高阶剪切及正交变形理论研究了Winkler-Pasternak弹性地基上功能梯度板的自由振动和弯曲响应.蒲育等[7]基于n阶广义剪切变形梁理论(GBT)研究了热-机载荷耦合作用下弹性地基功能梯度材料梁的振动特性和稳定性.滕兆春等[8]基于Timoshenko梁理论,采用微分变换法(differential transform method,DTM)研究了弹性地基上转动功能梯度材料Timoshenko梁的自由振动,分析了边界条件、转速、弹性地基模量和梯度指数对横向自由振动无量纲固有频率的影响.李万春[9]等基于Euler-Bernoulli曲梁理论,分析了曲率变化系数和材料体积分数对变曲率功能梯度材料拱面内自由振动频率的影响.Sayyad等[10]在考虑剪切变形和转动惯量影响的基础上应用各种等效的单层壳理论研究了功能梯度材料双曲壳的静态和自由振动响应.上述工作大多在功能梯度材料的理想状态建立力学模型并进行力学分析,忽略了实际应用中材料孔隙的存在.

功能梯度材料在实际制备和生产中,由于制备方式和工艺的缺陷,使得材料内部往往产生微小孔隙.孔隙对功能梯度材料的剪切强度、弯曲强度和模量、拉伸强度和模量、压缩强度和模量等有着较大的影响.已有一些学者对多孔功能梯度材料结构的静动态力学行为展开研究.其中,Shafiei等[11]对多孔功能梯度材料双向锥形纳米梁的力学行为进行了计算和分析.结果表明多孔体积分数、功能梯度指数以及横截面的改变对多孔功能梯度材料双向锥形微、纳米梁的屈曲行为有较大的影响.Akba[12]研究了多孔功能梯度材料梁在动载荷作用下的受迫振动问题,计算并分析了孔隙率参数、材料分布和孔隙率模型对功能梯度材料梁受迫振动响应的影响.滕兆春等[13]基于经典薄板理论,考虑孔隙和梯度指数对功能梯度材料弹性常数的影响,采用DTM研究了四边受压多孔功能梯度材料矩形板的自由振动和屈曲特性.以上研究结果显示,孔隙对功能梯度材料结构的静动力响应有着直接的影响,因此对多孔功能梯度材料结构在不同工作环境和工况下的力学行为进行分析研究具有重要意义.

目前,对于热环境中多孔功能梯度材料转动梁的研究还鲜有文献报道.本文基于Timoshenko梁理论和物理中面的概念并考虑均匀孔隙分布模型以及材料的温度依赖特性,建立热环境中多孔功能梯度材料转动Timoshenko梁横向自由振动的控制微分方程,采用微分变换法(DTM)对自由振动的无量纲控制微分方程及边界条件进行变换求解来研究其固有频率特性.将其退化为常温下无转速无孔隙的功能梯度材料Timoshenko梁的自由振动,得到无量纲固有频率和已有文献结果对照,以验证DTM求解的有效性和正确性.在计算结果的基础上,进一步分析边界条件、孔隙率、转速、温度、梯度指数和细长比对多孔功能梯度材料 Timoshenko梁无量纲固有频率的影响.

1 数学模型及材料物性参数的描述

考虑如图1所示热环境中转动的多孔功能梯度材料 Timoshenko矩形截面梁,取梁的轴线方向和厚度方向分别为x轴和z轴,建立笛卡尔三维坐标系xyz.梁的长为L,宽为b,高为h,绕z轴以角速度μ转动,坐标系中x轴和y轴随梁一同转动.

图1 多孔功能梯度材料转动Timoshenko梁的几何模型Fig.1 Geometric model of a porous functionally graded material rotating Timoshenko beam

多孔功能梯度材料 Timoshenko梁考虑仅由陶瓷和金属两种材料复合而成.梁的下表面为完全金属,上表面为完全陶瓷,两表面之间材料成分连续变化且包含微小孔隙,这样材料性质沿厚度方向呈梯度分布,梁的物理性质参数P(弹性模量E、切变模量G、质量密度ρ、热膨胀系数α、泊松比ν等) 均是关于坐标z、温度T和孔隙率θ的函数.考虑均匀孔隙分布,功能梯度材料梁的物性参数可由下列混合律模型[14]统一给出

(1)

式中：n为功能梯度材料的梯度指数;下标c表示陶瓷;m表示金属.考虑材料物性参数的温度依赖性,则陶瓷和金属材料的物性参数由文献[15]可表示为

P(T)=P0(P-1T-1+1+P1T+P2T2+P3T3)

(2)

式中：P0、P-1、P1、P2和P3是与温度有关的系数,且不同材料所对应的系数不同.该数值由实验直接给出,其值具体可见文献[7]中表1.T=ΔT+T0为当前温度,T0为初始温度,这里取T0=300K,ΔT为温度变化.

2 控制微分方程及参数的无量纲化

假设z=z0为多孔功能梯度材料 Timoshenko梁的物理中面,其计算公式为[16]

(3)

对于功能梯度材料转动Timoshenko梁,Ganguli等[17]给出的几何方程为

(6)

式中：u0、w分别为物理中面上任一点关于x、z轴方向的位移；φ表示梁横截面的转角；εxx表示梁截面上任一点的线应变；γxy和γxz表示切应变.则由弯曲应变产生的弯曲应变能为

(7)

将式(4)代入式(7)得

(8)

将式(8)展开并忽略某些高阶小量得到

(9)

定义如下系数A1、A2、B1和B2：

式中：A1、A2、B1和B2分别称为梁的拉伸刚度、弯曲刚度、惯性系数和转动惯量.

多孔功能梯度材料转动Timoshenko梁沿x轴方向的离心力FC为

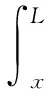
(10)

由离心力产生的物理中面上一点的应变与轴向位移的关系为

(11)

联立式(9～11),得到梁的弯曲应变能为

(12)

式中：C1为常数.由剪切变形产生的应变能为

(13)

将式(5,6)代入式(13)得

(14)

式中：C为剪切刚度；ks为剪切修正系数.由于本文分析的梁为矩形截面,根据参考文献[18]取ks=5/6.再将式(12)与式(14)相加,得梁的总应变能为

(15)

梁的动能为

(16)

(17)

对热环境影响下的多孔功能梯度材料转动 Timoshenko梁,采用Hamilton原理[19]

(18)

式中：Π、U和W分别为系统的动能、弹性势能和外力所做功;δ表示变分符号;t1和t2分别表示梁运动的开始时间和结束时间.

将式(15～17)代入式(18),可得热环境影响下多孔功能梯度材料转动Timoshenko梁横向运动的控制微分方程组

对于功能梯度材料梁的自由振动,可令

(20)

(21)

将式(20)和式(21)代入式(19),得到热环境影响下多孔功能梯度材料转动Timoshenko梁自由振动的控制微分方程组

对上式进行如下无量纲化

式(22)经无量纲化后,可得热环境影响下多孔功能梯度材料转动Timoshenko梁自由振动的两个控制微分方程

取梁在实际工程中较常见的边界条件：

固支(C)：

(24)

简支(S)：

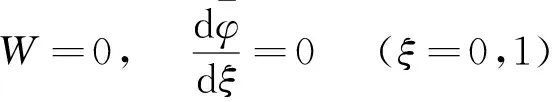
(25)

自由(F)：

(26)

3 控制微分方程及边界条件的DTM变换

对边界条件也进行DTM变换：

在ξ=0处：

固支(C)：

W1[0]=0,W2[0]=0

(28)

简支(S)：

W1[1]=0,W2[0]=0

(29)

在ξ=1处：

固支(C)：

(30)

简支(S)：

(31)

自由(F)：

(32)

4 计算结果及分析

边界条件式(28～32)和DTM变换后的热环境中的多孔功能梯度材料转动Timoshenko梁自由振动的代数特征方程(27)通过MATLAB编程进行迭代求解即可得到给定精度要求的无量纲固有频率.

表1 C-C边界条件下的功能梯度材料 Timoshenko梁一阶无量纲固有频率Tab.1 First order dimensionless natural frequencies of FGM Timoshenko beams with C-C boundary conditions

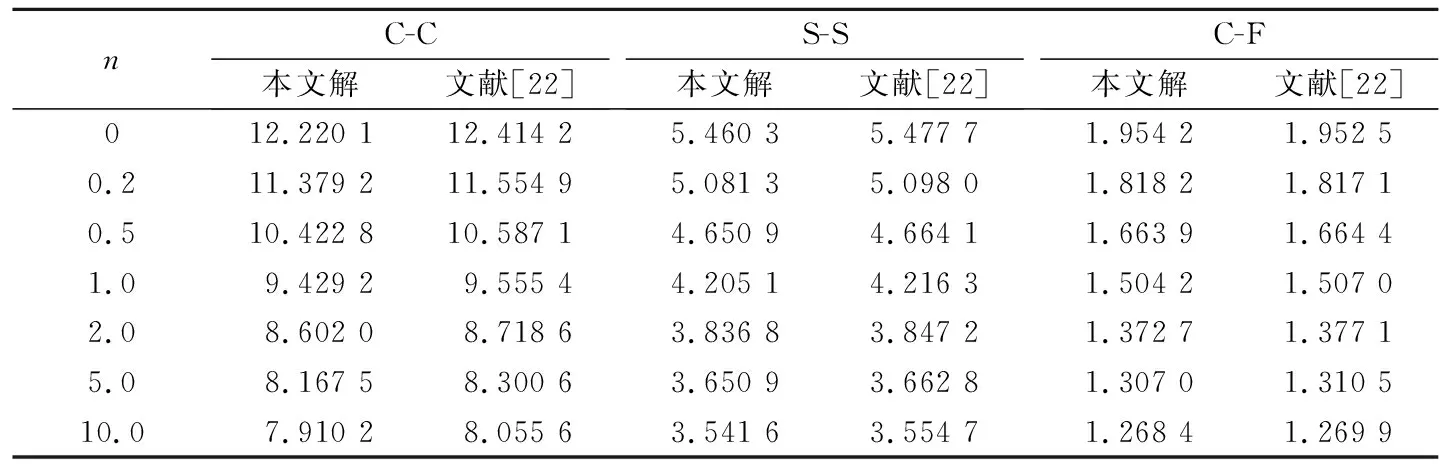
表2 不同边界条件下功能梯度材料 Timoshenko梁的一阶无量纲固有频率(h/L=1/20)Tab.2 First order dimensionless natural frequencies of FGM Timoshenko beams with different boundary conditions(h/L=1/20)

表1给出了在C-C边界条件下,分别取细长比h/L为1/20、1/30和1/50,梯度指数n为0、0.5、1.0、2.0、5.0时,无转速的功能梯度材料 Timoshenko梁通过DTM求解出的一阶无量纲固有频率与文献[18]的Chebyshev 配点法所求的数值结果进行的比较.可以看出本文所得结果与其比较接近.

表2给出了梁在不同边界条件下,取细长比h/L为1/20,功能梯度指数n分别为0、0.2、0.5、1.0、2.0、5.0、10.0时,通过DTM求解出的一阶无量纲固有频率,与文献[22]所使用的Rayleigh-Ritz 法算得的数值结果进行的比较,可看出本文结果与其相接近.根据表1和表2这两个算例,说明了DTM对于研究本问题的有效性与正确性.

功能梯度指数n、无量纲转速η、变化温度ΔT、孔隙率θ等不同参数对频率的影响.对于热环境影响下多孔功能梯度材料转动 Timoshenko梁,取陶瓷和金属材料分别为ZrO2和Ti-6Al-4V,环境的初始温度为300 K,两种材料的弹性模量、热膨胀系数和密度的温度相关系数见文献[7]中表1(P-1和P3均为0).

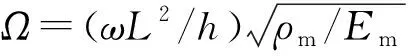
图2 C-S边界条件下梯度指数n和孔隙率θ对功能梯度材料Timoshenko梁前三阶的无量纲固有频率Ω的影响Fig.2 The effects of gradient exponent n and porosity θ on the first three dimensionless natural frequencies the first three dimensionless natural frequencies Ω of FGM Timoshenko beams under C-S boundary conditions

图3 C-F边界条件下梯度指数和孔隙率对功能梯度材料Timoshenko梁前三阶的无量纲固有频率Ω的影响Fig.3 The effects of gradient exponent n and porosity θ on the first three dimensionless natural frequencies the first three dimensionless natural frequencies Ω of FGM Timoshenko beams under C-F boundary conditions

图4表示了梁在四种边界条件下,取无量纲转速η=5、梯度指数n=1、细长比h/L=1/20和孔隙率θ=0.1时,梁前三阶的无量纲固有频率与变化温度ΔT的关系曲线.由图可看出,同样在C-F边界的一阶无量纲固有频率与温度呈正相关,其余无量纲固有频率随升温都呈现下降趋势,其中,C-C、C-S和C-F三种边界条件下的无量纲固有频率的下降明显程度：三阶无量纲固有频率>二阶无量纲固有频率>一阶无量纲固有频率；而S-S：一阶>三阶>二阶,且S-S的无量纲一阶固有频率在ΔT到达475 K后降到0,由弹性稳定性理论可知,梁在此温度下将进入临界屈曲状态,该温度对应为屈曲临界温度.

图4 不同边界条件和变化温度ΔT对功能梯度材料Timoshenko梁前三阶的无量纲固有频率Ω的影响Fig.4 The effects of different boundary conditions and varying temperatures ΔT on the first three dimensionless natural frequencies Ω of FGM Timoshenko beams

图5表示了热环境影响下多孔功能梯度材料转动Timoshenko梁在变化温度ΔT=300 K、梯度指数n=1、细长比h/L=1/20、孔隙率θ=0.1和C-C、C-S、S-S和C-F四种不同边界的条件下,梁前三阶的无量纲固有频率与无量纲转速η的关系曲线.由图可看出,不同边界条件下无量纲固有频率都随无量纲转速η的增加而增加.其中在C-C、C-S、S-S三种边界条件下的无量纲固有频率随无量纲转速η增加而增加的明显程度：一阶无量纲固有频率>二阶无量纲固有频率>三阶无量纲固有频率；在C-F时：二阶>三阶>一阶.

图5 不同边界条件和无量纲转速η对功能梯度材料Timoshenko梁前三阶的无量纲固有频率Ω的影响Fig.5 The effects of different boundary conditions and dimensionless rotational speed η on the first three dimensionless natural frequencies Ω of FGM Timoshenko beam

5 结论

本文基于Timoshenko梁理论,考虑材料的温度依赖性质并确定梁的物理中面,利用Hamilton原理导出对于孔隙均匀分布的多孔功能梯度材料梁在热环境中转动时横向自由振动的控制微分方程.采用微分变换法(DTM)对热环境中转动多孔功能梯度材料Timoshenko梁的自由振动问题进行分析和求解.选取具体算例,将求解结果与文献结果对比,验证了求解方法的有效性和正确性.分析了不同边界条件下孔隙均匀分布的功能梯度材料梁的孔隙率、无量纲转速、温度、细长比和梯度指数对多孔功能梯度材料转动Timoshenko梁无量纲固有频率的影响.

1) 随着梯度指数n的增加,C-F边界条件下一阶无量纲固有频率呈现增大趋势,其余无量纲固有频率都呈现下降趋势,且阶数越高变化越明显.

2) C-F边界条件下一阶无量纲固有频率随升温而上升,其余无量纲固有频率都随升温而下降, S-S边界条件下的无量纲固有频率的下降程度在一阶最为明显,其余的无量纲固有频率的下降程度在高阶最明显；S-S的一阶无量纲固有频率在ΔT到达475 K后降到0,表示梁将进入临界屈曲状态.

3) 无量纲固有频率均与无量纲转速η呈正相关.在C-C、C-S、S-S三种边界条件下,其无量纲固有频率由无量纲转速η增加而增加的程度在一阶最明显；在C-F边界条件下,其上升程度在二阶最明显.