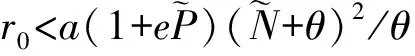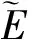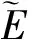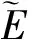具恐惧效应和配偶相遇的扩散捕食系统分析

刘 洋，刘宇鑫，郑 巍

(黑龙江大学数学科学学院，黑龙江 哈尔滨 150080)

0 引言

捕食关系是自然界中最基本的关系之一，捕食者通过捕食对食饵产生影响.许多学者研究了捕食者-食饵系统，并分析了其动力学性质[1-2].在捕食过程中捕食者不仅可以直接捕杀食饵，也可以对食饵产生间接影响，形成一种捕食者恐惧效应.文献[3]提出了一个具食饵恐惧效应的捕食者-食饵系统，研究了恐惧效应对捕食者-食饵系统结构的影响，指出恐惧效应能够稳定捕食者-食饵系统.在此基础上，结构更加复杂的具恐惧效应的3种群系统被讨论[4-6].种群空间结构的存在能够影响捕食者-食饵系统，使其产生更为复杂的动力学行为，因而一些学者研究了具恐惧效应的扩散捕食者-食饵系统[7-10].

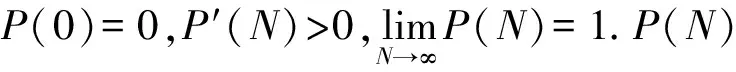
基于上述讨论，本文将考虑如下一类具恐惧效应与配偶相遇的扩散捕食者-食饵系统：

(1)

其中Ω是n(n≥1)中带有光滑边界∂Ω的有界区域，并且c∈[0，1).系统(1)中的变量、参数以及它们的生物意义见表1.本文的主要目的是研究系统(1)的动力学性质.

1 解的全局存在性与耗散性

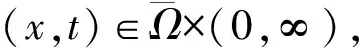
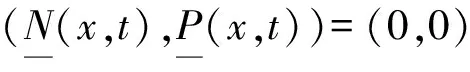
dN/dt=r0N-dN-aN2，dP/dt=bP-mP-δP2+chNP，

∂N/∂t≤d1ΔN+r0N-dN-aN2，x∈Ω，t>0，

定理2 假设(N，P)是系统(1)的任意一个解.若r0>d且ch(r0-d)+a(b-m)>0，则

(2)

证明直接计算得

∂N/∂t≤N(r0-d-aN)，x∈Ω，t>0，

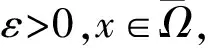
∂P/∂t≤d2ΔP+[b+ch(r0-d)/a+ε)-m-δP]P，x∈Ω，t≥T，

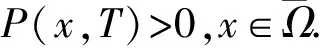
2 常值稳态解

系统(1)的常值稳态解有

其中：

(3)

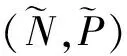
(4)

令Λ∶={μi|0=μ0<μ1<…<μi<…}是齐次Neumann边界条件的算子-Δ的特征值.定义

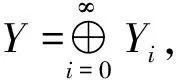
(5)

其中(φ，ψ)∈Y，并且

b21=chP，b22=b-m-2δP+chN.

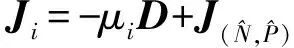
λ2-Tiλ+Di=0，i∈0，

(6)

其中

定理3E0总是存在的，若b>m，则E0是局部渐近稳定的.

证明由(6)式知在E0处的特征方程为

λ2-(-(d1+d2)μi+d-(b-m))λ+(d1d2μi+(d1(m-b)+d2d)μi-(b-m)d)=0.

若b

在Ek，k=1，2处的特征方程为

定理5 若b>m，则E3存在且局部渐近稳定的.

证明当b>m时，则E3存在，且由(5)式可得

则系统(1)在E3处线性化系统对应的特征方程为

(λ+d2μi+d+h(b-m)/δ)(λ+d1μi+b-m)=0.

对任意i∈0，特征值实部均为负的，因而E3是局部渐近稳定的

设F(N)=c3N3+c2N2+c1N+c0，其中

c3=-ehc(hc+aδ)/δ2，

c2=-a-(ech(d+a)+ea(b-m)+ch2)/δ-h2ec(b-m)(2δ-ch)/δ2，

c1=r0-d-aθ-((b-m)(ed+ea+h+2h2eθc)+eθdch)/δ-h(b-m)[ch+e(b-m)]/δ2，

c0=-dθ-θ(b-m)(ed+h)/δ-heθ(b-m)2/δ2.

定理6 (ⅰ)系统(1)可能不存在或者存在1个、2个或3个正平衡点，见表2；

表2 系统(1)平衡点存在条件

(7)

(8)

(2)若c0>0，即e(b-m)[h(b-m)+δd]<δ[h(b-m)+δd]，可得系统(1)有1个或者3个正平衡点；

综上所述，结论(ⅰ)得证.

(9)

故得到Di>0，则结论(ⅲ)得证.

3 图灵不稳定性

(10)

证明(ⅰ)和(ⅱ)是显然成立的.对于固定的d2>0，可得

利用Matlab对前面得到的图灵不稳定性结果进行数值模拟.令r0=0.7，e=0.1，θ=0.1，a=0.2，c=0.2，δ=0.55，b=0.3，d=0.25，h=0.4，m=0.1，d1=0.000 1，d2=3.5，b=0.2.图1显示由扩散导致图灵不稳定性(见定理7)，表明捕食者与食饵共存于一个非常值稳态解.

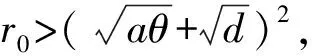
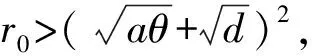
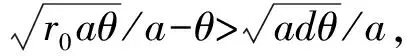
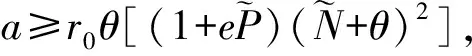
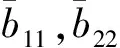
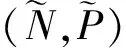
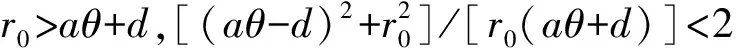
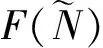
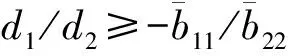
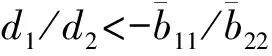
图1 图灵不稳定性