n元强正态分布的性质及其参数估计
2023-01-16刘虹曼李树有
刘虹曼,李树有
(1.辽宁理工学院基础教学部,辽宁 锦州 121000;2.辽宁工业大学理学院,辽宁 锦州 121001)
1 预备知识
1.1 强正态分布
强正态分布是偏态分布[1-2]的一种.1985年,Azzalini首次提出偏态分布理论.2007年,Gupta[3]在利用偏态分布分析偏态单峰密度的数据时通过大量的模拟研究,提出了一种可行性较强的倾斜模型,将正态分布作为其中的一个特例,命名为强正态分布,并做出如下定义:
如果随机变量X具有累积分布函数[4]
FX(x;α)=P(X≤x)=(Φ(x))α,-∞
则称其服从强正态分布,其中Φ(·)表示标准正态分布的分布函数[5].
1.2 Capula函数
1998年,Nelsen提出了Copula函数[6],并给出了定义及基本性质.Copula函数描述的是变量间的相关性,实际上是一类将联合分布函数与它们各自的边缘分布函数连接在一起的函数,因此也被叫作连接函数.
令u=(u1,u2,…,un),∀u1,u2,…,un∈[0,1],Copula函数表示为C:[0,1]n→[0,1],对于(x1,x2,…,xn)∈(-∞,∞)×(-∞,∞)×…×(-∞,∞),称
FX1,X2,…,Xn(x1,x2,…,xn)=C{FX1(x1),FX2(x2),…,FXn(xn)}
为连接函数.
2 主要结果
2.1 n元强正态分布的性质
由Clayton连接函数的定义,有n元Clayton连接函数
即对α>0,(U1,…,Un)有联合分布函数[7]
Gupta于2013年得到如下结论[8]:
(1)对0 (2)对m (3)对0 (4)已知U1=u1,…,Um=um,(Um+1,…,Un)的条件概率密度函数为 分布函数为 FX1,X2,…,Xn(x1,x2,…,xn)= P{X1≤Φβ1(x1),X2≤Φβ2(x2),…,Xn≤Φβn(xn)}= Cα,n(Φβ1(x1),Φβ2(x2),…,Φβn(xn))= (Φ(x1)-β2/α+Φ(x2)-β2/α+…+Φ(xn)-βn/α-(n-1))-α, 随机变量(X1,…,Xn)的联合概率密度函数为 如果对于参数β1>0,β2>0,…,βn>0,随机变量(X1,…,Xn)有上述联合分布函数FX1,…,Xn(x1,…,xn),则随机变量(X1,…,Xn)服从n元强正态分布,并有以上概率密度函数fX1,…,Xn,记作(X1,…,Xn)~MPN(α,β1,β2,…,βn). 根据以上定义,得到如下性质: 性质如果随机变量(X1,…,Xn)服从n元强正态分布,那么: (1)X1~PN(β1),X2~PN(β2),…,Xn~PN(βn); (2)随机变量(X1,…,Xn)的联合概率密度函数为 (3)随机变量(X1,…,Xn)的联合分布函数为 FX1,X2,…,Xn(x1,x2,…,xn)= (Φ(x1)-β1/α+Φ(x2)-β2/α+…+Φ(xn)-βn/α-(n-1))-α; (4)随机变量(X1,…,Xn)的联合生存函数为 (5)已知X1=x1,X2=x2,…,Xm=xm,则(Xm+1,…,Xn)的条件概率密度函数为 条件分布函数为 证明对于上述性质(1),当n元随机变量(X1,…,Xn)服从n元强正态分布时,根据Clayton连接函数的性质可知结论显然成立.性质(2)可以通过对n元联合分布函数进行求导计算得到.对于性质(3)和性质(4),可以分别根据n元联合分布函数和n元联合生存函数定义求得,即: FX1,…,Xn(x1,…,xn)=P{X1≤Φβ1(x1),X2≤Φβ2(x2),…,Xn≤Φβn(xn)}= Cα,n(Φβ1(x1),Φβ2(x2),…,Φβn(xn))= (Φ(x1)-β1/α+Φ(x2)-β2/α+…+Φ(xn)-βn/α-(n-1))-α; 对于性质(5),根据条件概率分布函数的定义,当X1=x1,X2=x2,…,Xm=xm时,有 即可求得条件分布函数 对其求导,即可得条件概率密度函数 为了估计n元强正态分布的未知参数α,α1,…,αn,设β1=αα1,β2=αα2,…,βn=ααn. 根据其已知概率密度函数推导出似然函数为 对其求对数得到对数似然函数为 分别对α,α1,α2,…,αn进行极大似然估计,即分别对α,α1,α2,…,αn求偏导,并使其等于零联立得到: 因为以上联立方程不能直接求出未知参数α,α1,…,αn的极大似然估计值,所以接下来利用牛顿迭代法对参数α,α1,…,αn的极大似然估计值进行进一步计算.令: 将函数f1,f2,f3,…,fn+1分别对参数α,α1,α2,…,αn-1,αn求偏导,则有: ⋮ ⋮ 依此进行下去,可得 由牛顿迭代法得到以下公式: 即 将中国各个主要城市的月降水量分为12组数据进行去差异化整理,整理结果如表1所示.将其作为样本数据[10](表1中对数据保留三位小数),对未知参数进行参数估计. 表1 中国各主要城市月降水量 对于以上12组数据,即n=12,利用Matlab对α1,α2,…,α12这12个未知参数进行估计,得到参数估计值(精度为第n次估计值与第n+1次估计值差的绝对值小于10-3): α=4.223,α1=0.704,α2=0.632,α3=0.656,α4=0.611,α5=0.706,α6=0.697, α7=0.802,α8=0.755,α9=0.674,α10=0.771,α11=0.734,α12=0.645. 根据所设参数β1=αα1,β2=αα2,…,βn=ααn,可计算出: β1=2.973,β2=2.669,β3=2.770,β4=2.580,β5=2.981,β6=2.943, β7=3.387,β8=3.188,β9=2.846,β10=3.256,β11=3.099,β12=2.724. 本文主要研究了n元强正态分布的各项性质,以及对未知参数的极大似然估计.主要得出以下结论: (1)推导得到了n元强正态分布具有联合概率密度函数、联合分布函数、联合生存函数、条件概率密度函数、条件分布函数的性质. (2)根据所取的样本数据,即180个中国部分主要城市的月降水量数据,对α1,α2,…,α12这12个未知参数进行估计,得到参数估计值(精度为第n次估计值与第n+1次估计值差的绝对值小于10-3)α1,α2,…,α12.根据所设参数β1=αα1,β2=αα2,…,βn=ααn,可计算出β1,β2,…,β12.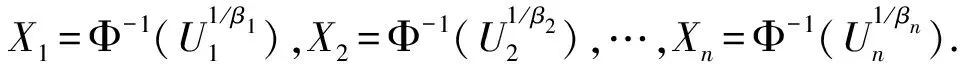
2.2 n元强正态分布的极大似然估计
2.3 应用实例

3 总结
