基于新课程标准的高中数学建模教学认知与策略

■ 广东省佛山市三水区实验中学 李 安

数学家、数学教育家Hans.Freudenthal指出：学数学就是学习数学化，教数学就是教会学生数学化。数学建模是一种很重要的水平数学化。在新课程标准理念下，有效开展数学建模教学，是高中数学新课程目标和内容的重要要求，是学科育人和创新人才培养的有效载体，是培养学生应用意识、合作精神、价值观念和问题解决能力的跨学科融通载体。但现实中教师对数学建模教学的认知堪忧。

一、高中数学建模教学存在的问题

（一）教学设计缺乏整体把握和研究

新课程改革越来越重视数学建模活动，但教师对数学建模教学内容的设计缺乏整体把握和研究，在课堂教学中只是适当开展数学建模教学，其教学内容设计基本是依照教材的实际情境直接给出数学模型、应用数学方法求解模型，其实质是“已知数学模型进行数学求解”，相当于单纯而机械的解题操练，没有呈现数学建模教学的整体设计，难以培养学生的建模素养。

（二）缺乏建模的全过程教学

《普通高中数学教科书》2019人教A版把“数学建模”编为必修和选择性必修课程内容，而且设置有专门的数学建模案例以呈现数学建模全过程教学。例如，人教A版（2019年）《数学》必修第一册第162页“建立函数模型解决实际问题”，此案例完整的展现了建模全过程的整体统一。但在教学中，多数教师还是沿用解决实际应用题的方式进行数学建模教学，少数教师虽关注建模教学的过程，但在教学过程中忽视实际情境、发现和提出问题、数据的收集与处理，忽视模型的检验与改进，重视模型的建立和求解，缺乏建模的全过教学。数学建模教学要注重建模的全过程教学，不能以解决实际情境问题的短期应试效应来设计教学内容，而忽视对学生建模素养培养的长期效应。

（三）缺乏跨学科融合与智能计算思维

数学是一切学科的基础。物理、化学、生物、地理、工程学、建筑学、信息学都离不开数学。但多数教师对实际情境问题的分析和模型的假设还局限在纯数学上，没有融合其他学科的知识，缺乏数学与现实问题及相关学科知识相融合的思维。教科书中设置的数学建模案例中经常会出现“由信息技术得”“用信息技术计算”等语句，其意是在数学建模教学中要借助信息技术和智能计算完成数据的收集和处理。但现实数学建模教学中，多数教师习惯纸笔运算或计算器运算。

二、基于新课程标准的高中数学建模教学认知

数学建模过程主要包括在实际情境中从数学的视角发现问题、提出问题，分析问题、建立模型，确定参数、计算求解，检验结果、改进模型，最终解决实际问题。数学建模六个过程的整体统一，突显了数学建模的全过程教学，体现了数学建模的综合教育价值。开展建模的全过程教学逐步实现数学建模素养的提升：对现实情境问题能用数学语言表达现实世界，发现和提出问题；对文字、图表、数据等信息进行分析、整理并建立模型；利用数据确定假设模型中的参数，通过计算求解得出数学模型；根据问题的实际意义检验结果，利用其他信息对模型作出改进、完善，并应用模型对现实问题进行解释、预测。学生通过参与数学建模活动的全过程，不仅感悟到数学与现实之间的关联，学会用数学模型解决实际问题，积累数学实践的经验，而且学习方式也能得到切实的转变，能以多样化的方式开展学习与实践活动，提升了跨学科思维和信息素养，增强了创新意识和科学精神。

信息化和智能化高速发展必将带来跨学科融合研究，数学建模教学突显了多学科融合特点，关注不同领域知识的融通。高中学科中物理的运动力学、天体运动，化学的晶体结构、电子模型，生物学的遗传规律、DNA模型，地理的遥感定位等都是数学建模与跨学科研究的主题。另外，工程学、建筑学、信息学、大学数学建模竞赛都有明显的跨学科内容。除此以外，现代生活、经济、科学、工程技术等很多领域无不融入数学建模，跨学科融通已经成为数学建模的重要特征。

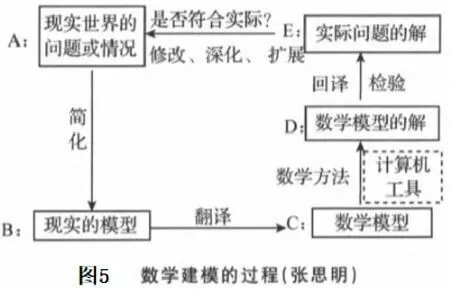
数学建模的实质是从“现实世界”到“数学世界”的转化过程，利用数学的解回答现实世界提出的问题，并为现实世界提供科学的推断或预测。现实世界中的数据量多且复杂，收集、整理数据需要智能软件和信息技术；利用数据确定假设模型中的参数，通过计算求解得出数学模型，根据问题的实际意义检验结果都需要大量的数据计算，把信息技术和智能计算融入数学建模教学，促使数学建模教学向更加广阔的空间迈进。张思明老师曾提出利用数字工具（如计算机工具）并结合数学方法求解数学模型，是建模循环中一个重要的步骤（如图5）。

三、高中数学建模教学策略

（一）注重价值引领是数学建模教学的核心

数学建模主要是解决现实世界遇到的生活、生产实践问题，而生活、生产实践往往涉及中华优秀文化、国家建设、经济发展、社会生产等，能引导学生关注中华优秀文化、社会热点和社会主义建设成果，增强民族自豪感，培育学生的核心价值观。“南水北调”工程是集生态、经济和社会于一体的国家战略性工程，输水槽是“南水北调”的控制性工程之一。教学中设计了“输水槽横截面形状对水流量大小影响”的建模教学案例，水槽横截面周长一定时，横截面形状是影响水流量的关键因素，基于生活经验和几何知识学生设计出如图6所示的水槽横截面图。数学建模是为了解释为什么出现这种规律进而作出模型假设，参数的设置是依据真实发生的数据更好地衡量现实问题变化的影响要素，模型的求解、检验和改进是依据数学运算、数据分析、逻辑推理等更好地衡量变化趋势的准确程度，应用模型对现实问题进行科学推断或预测，使得现实问题发展的结果可测、可控，对未知的世界提出更好的方案和科学的预测，解释及预测是数学建模教学的价值旨向。输水槽横截面周长一定时，横截面形状为什么是影响水流量的关键因素，将实际问题情景理想化而做出模型假设：假定水流速度是一定的，那么，要在单位时间内获得最大的流水量，就应该将水槽设计成横截面面积最大，而截面面积又与截面周长有关，基于实际可再假定横截面的周长a一定（图6中各横截面图形的实线段之和为定值a）。这样的话就可以设置参数建立截面面积S的数学模型，应用数学运算（信息技术和智能计算）、数据分析、逻辑推理得出把截面设计为半圆形时，单位时间内获得最大水流量。这与在生活中同学们观察到的输水槽横截面形状大多为半圆形是一致的。同时，通过对模型的求解、检验和改进，学生体验到当n越大截面的面积也越大，n趋近于+∞时横截面就趋近于半圆，从而科学解释了通常情况下水槽的形状设计为半圆形的原因。

图6 水槽横截面形状示意图

（二）教师的专业素养和认知是数学建模教学的保障

（三）实切的问题情境是数学建模教学的基础

高中数学建模教学是培养学生建模素养的重要途径，实切的问题情境能促进学生提出更为全面、更有价值的问题，激发学生学习的兴趣，又能培养学生的开放思维，提高学生的实践和创新能力。生产、生活实践中真实发生的、切合学生生活的情境问题是开展数学建模教学的基础。学生在生活和实践中会发现、体验大量的数学建模案例，比如学校建筑物的高度、高中生的身高与体重的关系、汽车安全停车距离、输水槽横截面的形状、广场停车场优化问题、社会核酸检查点的位置规划、共享单车停放点的规划、洗衣服漂洗次数问题、泡茶所用水温与茶的口感问题……只要我们善于观察、思考，就能发现生活、实践中有很多实切的情境问题。