对SNOW 系列算法相关攻击所需连续密钥字最低个数的分析*

孙 莹

（中国人民解放军战略支援部队信息工程大学，河南 郑州 450001）

0 引言

由于线性反馈移位寄存器（Linear Feedback Shift Register，LFSR）产生的序列周期长、统计特性好，在序列密码设计中是一种常用的初始伪随机数发生器。基于LFSR 和有记忆变换的前馈模型序列密码的基本思想是，利用非线性变换对LFSR 的输出序列进行进一步加工，破坏其线性制约性，从而获得更好的伪随机性。以SNOW 系列算法为典型代表，这类序列密码算法由于具有良好的实现性能和安全性，在加密通信等方面占据着重要位置。SNOW 系列算法在实际中有着广泛的应用。2002 年，SNOW 2.0[1]由国际标准化组织（Internation Organization for Standardization，ISO）作为国际标准ISO/IEC 18033-4 发布。2018 年提出的SNOW-V[2]以及之后提出的升级版本SNOW-Vi[3]则参与了5G加密标准的评选。

对于这类序列密码算法，相关攻击是最强有力的分析方法之一。相关攻击是一种已知明文攻击，其基本思路是利用密钥流输出和LFSR 序列的相关性，通过分割穷举LFSR 初态的方式对初始密钥进行还原。相比于采用无记忆变换作为滤波函数的序列密码，这类基于有记忆变换和LFSR 的序列密码算法需要多个时刻的密钥字来构造只包含密钥字和LFSR 序列的线性逼近作为相关攻击区分器，从而实施相关攻击。以往关于SNOW 2.0 的相关攻击研究中均给出了包含两个连续时刻密钥字的区分器构造[4-8]，而对于完整版本的SNOW-V 和SNOWVi，已有的相关攻击研究均是基于包含3 个连续时刻密钥字的相关攻击区分器展开[10-11]。这些分析结果逐步明确了这些算法具有抗相关攻击的安全性，但并没有从理论上解释SNOW 2.0 的单密钥字以及SNOW-V 的连续两个时刻密钥字是否与相应的LFSR 序列存在相关性。

本文采用基于Walsh 谱理论的复合函数构造方法，将SNOW 2.0、SNOW-V 和SNOW-Vi 序列密码算法的相关攻击区分器等价地转化为相应的复合函数的线性逼近问题。通过证明复合函数的线性逼近中包含的线性逼近单链的相关系数始终为零，对SNOW 2.0、SNOW-V 和SNOW-Vi 序列密码算法与LFSR 序列相关免疫的最大连续密钥字的长度给出了明确的结论。这些结论从理论上证明了对SNOW 2.0、SNOW-V 和SNOW-Vi 序列密码算法的相关攻击所需要的连续密钥字的最低个数，从而为这些算法的相关攻击研究提供了理论支撑。

本文其余部分组织如下：第1 节给出文中用到的符号及其定义，并简要介绍SNOW2.0、SNOW-V和SNOW-Vi 序列密码算法；第2 节证明SNOW 2.0的单密钥字与其LFSR 序列的相关免疫；第3 节给出SNOW-V 和SNOW-Vi 连续两个时刻密钥字与LFSR 序列的相关免疫性；第4 节总结全文。

1 预备知识

1.1 符号及定义

本文中将用到的符号及其定义如表1 所示。

表1 符号说明

引理1 说明，对于模232加运算，输入、输出mask 的最高非零位在同一位置是其线性逼近的相关系数非零的必要条件。

1.2 SNOW 2.0 算法简介

式中：矩阵乘法定义在由本原多项式z8+z4+z3+z4+1 ∈F2[z]定义的有限域上，z和z+1 分别为有限域上的2 倍乘和3 倍乘运算；SR为美国高级加密标准（Advanced Encryption Standard，AES）的S 盒。关于SNOW 2.0 序列密码算法的更多细节可参考文献[1]。

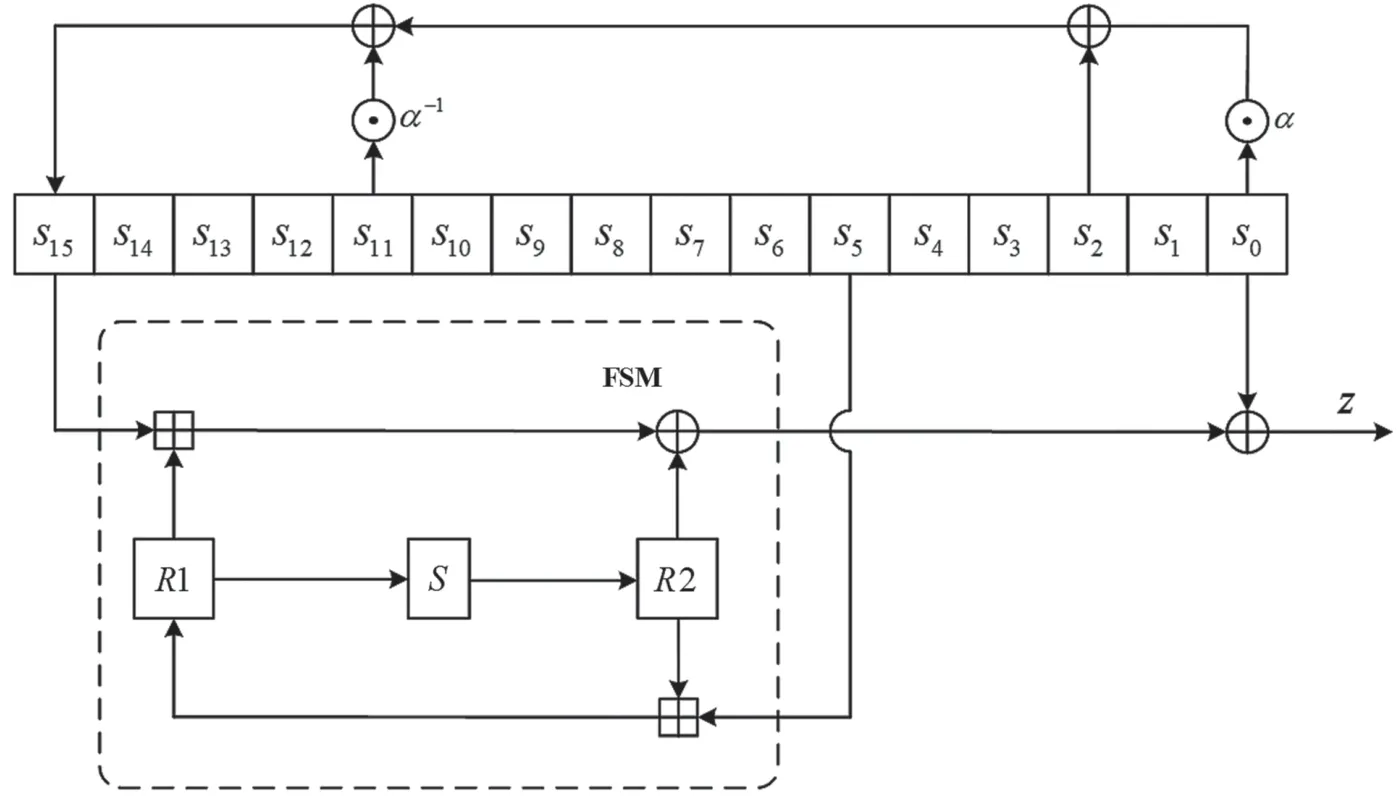
图1 SNOW 2.0 序列密码算法结构

1.3 SNOW-V 及SNOW-Vi 算法简介

SNOW-V 由LFSR 和FSM 部分组成，其中，LFSR 部分采用了两个移存器串联的模式，FSM 部分包含3 个记忆模块，每个记忆模块的规模为128 bit。其逻辑框架如图2 所示。

图2 SNOW-V 序列密码算法结构

式中：E(·)为子密钥为零的AES 算法的轮函数；σ变换为基于8 比特字的置换，具体为σ={0,4,8,12,1,5,9,13,2,6,10,14,3,7,11,15}，其中0 和15 是两个不动点。第t时刻输出的128 bit 密钥字为。对于SNOW-V 序列密码算法的更详细介绍可参考文献[2]。

相较于SNOW-V，2021 年提出的SNOW-Vi 变更了LFSR 的刷新方式以及LFSR 抽头位置，FSM则保持不变。SNOW 3G 的FSM 结构同样采用3 个记忆模块。当将σ变换替换为恒等变换，将位宽修改为32 bit，AES 轮函数替换为列混合和S 层组成的SP 结构，并增加一个密钥字的白化过程，则SNOW-V 的FSM 部分转变为SNOW 3G 的FSM。有关SNOW 3G 和SNOW-Vi 的详细介绍可参考文献[2]和文献[3]。

2 SNOW 2.0 的单密钥字与其LFSR 序列的相关免疫性

自2002 年SNOW 2.0 被提出以来，已经出现了许多相关攻击方面的研究[4-9]。这些研究均围绕着SNOW 2.0 两个连续时刻密钥字与其LFSR 序列的相关性展开，但还没有理论解释为何不采用单密钥字和LFSR 序列来构造线性逼近作为相关攻击区分器。对于非退化的LFSR 而言，其某一时刻的状态即为LFSR 序列的一个极大线性无关组，因此考虑形式为α×zt⊕(β0,β1,…,β15)×(st,st+1,…,st+15)0 的线性逼近，其中，α,β1,β2,…,β5∈为线性mask。由zt=(st+15R1t)⊕R2t⊕st，取R1t,R2t,st,st+1,…,st+15为自变量构造函数，f(x1,x2,y0,y1,…,y15)=(y15x1)x2⊕y0，则有：

式中：ρf=Wf(0,0,β0,β1,…,β15→α)。该逼近方程与题设中的线性逼近完全一致，因此ρ=ρf。

性质1 将SNOW 2.0 的只包含单个密钥字的区分器转化为了对函数f的线性逼近，使得本文可以从函数f的线性逼近的角度考察这一类线性逼近的相关系数。事实上，还可以对函数f的这一线性逼近进行更加细致的推导。不取定输入变量时，对函数f的线性逼近(0,0,β0,β1,…,β15)α的逼近 方程为：

上述结论表明，SNOW 2.0 的单个时刻密钥字与LFSR 序列不存在线性相关性，因而至少需要两个连续时刻的密钥字，才能构造SNOW 2.0 的相关系数非零的相关攻击区分器。

3 SNOW-V 和SNOW-Vi 连续两个密钥字与LFSR 序列的相关免疫性

自2018 年SNOW-V 被提出以来，针对SNOW-V 及其各类变形版本的相关攻击研究均围绕连续3 个时刻密钥字与其LFSR 序列的相关性展开[10-11]，但均未对不采用连续两个时刻密钥字与LFSR 序列的相关性进行相关攻击的原因作出理论解释。由于为SNOW-V 的LFSR的一个极大线性无关组[10]，考虑SNOW-V 的包含连续两个时刻密钥字的相关攻击区分器的形式为：

式中：ρf=Wf(0,0,0,a0,a1,a2,a3→α,β)。该逼近方程与题设中的线性逼近完全一致，因此ρ=ρf。

采用相同的方法，需要对这一复合函数的线性逼近过程中包含的线性逼近单链进行更细致的考察。记f1的输出mask 为(ξ1,ξ2,ξ3,ξ4,ξ5,ξ6)，f2的输出mask 为(η1,η2,η3,η4)，则有：

它等价于：

上式转化为ξ1×x⊕a1×u1⊕ξ2×(xu1)1ρ=0，亦即对模232加运算的线性逼近(ξ1,a1→ξ2)，因此ρ1=ρA(ξ1,a1→ξ2)。

函数f2的线性逼近方程为：

由上述mask 间的关系，逼近方程等价于：

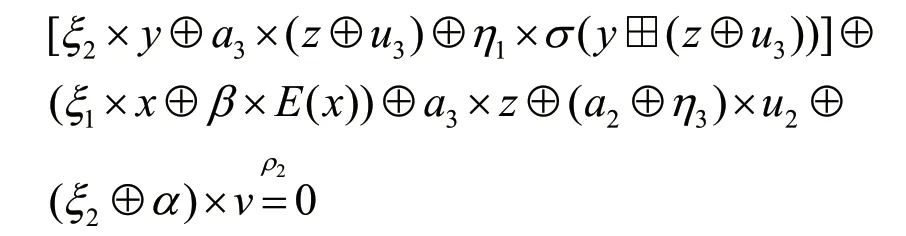
记r=z⊕u3，由z与u3独立知r与z独立，因此由ρ2≠0 知η3=a2，ξ2=α，a3=0。

由η1×σ(yr)=η1×σ(yr)T=(η1σ)·(yr)，可得(ξ2×y⊕0×r⊕(η1σ)×(yr))⊕(ξ1×x⊕β×E(x))0，即对模223加运算的线性逼近(ξ2,0 →η1σ)和 对AES 轮函数的线性逼近(ξ→β)，因此ρ2=ρA(ξ2,0 →η1σ)ρE(ξ1→β)。

由引理1，当ρA(ξ2,0 →η1σ)≠0 时有ξ2=η1=0，因此α=ξ2=0。再由ρ3=ρA(η1,η3→β)≠0 和ρ1=ρA(ξ1,a1→ξ2) ≠0 可知，η3=β=ξ1=a1=0，进而有a2=η3=0。

综上，对于ρ1ρ2ρ3≠0 的线性逼近单链，必有α=β=a0=a1=a2=a3=0，此时ρ=1，该线性逼近退化为平凡线性逼近0=0。因此，对任意不全为零的α,β,a0,a1,a2,a3，上述线性逼近的相关系数均为零。由定义1 知SNOW-V 的两个连续时刻密钥字与其LFSR 序列相关免疫。

相较于SNOW-V，由于SNOW-Vi 并未对FSM部分进行变更，上述结论和推理对于SNOW-Vi 同样成立。因此，对于SNOW-V 和SNOW-Vi，本文均得到两个连续时刻密钥字与其LFSR 序列相关免疫的结论。

4 结语

SNOW 系列序列密码算法是加密通信领域十分重要的序列密码算法，全面考察这些算法抵抗相关攻击的能力是十分必要的。基于复合函数的Walsh谱理论，本文构造相应函数，将只包含密钥字和LFSR 序列的线性逼近转化为对相应函数的线性逼近，对SNOW 2.0、SNOW-V 和SNOW-Vi 序列密码算法与LFSR 序列相关免疫的最大连续密钥字的长度给出了明确的结论。这些结论从理论上给出了对SNOW2.0、SNOW-V 和SNOW-Vi 序列密码算法的相关攻击所需要的连续密钥字的最低个数，为这些算法的相关攻击研究提供了理论支撑。