OFDM 双向中继系统中的功率分配优化策略*
2023-01-16沈先丽徐友云徐少红
沈先丽,徐友云,王 健,徐少红
(1.中车南京浦镇车辆有限公司,江苏 南京 210031;2.南京邮电大学,江苏 南京 210003;3.国防科技大学,安徽 合肥 230037)
0 引言
随着社会信息化程度不断提高,人们对移动数据业务的灵活性与多样化的要求越来越高,移动数据流量也在逐年成倍增加。正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术[1]由于具有高频谱利用率以及很好的抗多径衰落能力等特点,已经广泛应用于现代通信系统。然而,在OFDM 系统中,频率选择性衰落造成不同的子载波具有不同的信道增益,信道质量较差的子载波会给OFDM 系统带来“木桶效应”,严重影响系统整体性能。为了解决信道衰落对OFDM 系统性能的影响,提高OFDM 系统误比特率(Bit Error Rate,BER)性能,文献[2]提出了子载波抑制技术,即仅使用信道质量较好的子载波来传输信息,而将信道质量较差的子载波抑制不用。子载波抑制技术能够有效克服信道质量较差的子载波带来的“木桶效应”,从而提高OFDM 系统传输的可靠性。因此,子载波抑制技术为进一步提高OFDM 系统传输可靠性提供了新的思路。
由于可以扩大基站覆盖范围、获得分集增益,协同中继技术[3]作为下一代无线通信系统中的关键技术之一引起了学术界和业界的广泛关注[4],其核心思想是利用中继节点将源节点发送的信息进行放大或者去噪之后转发给目的节点[5]。中继处理信号的方式分为很多种,其中,放大转发(Amplifyand-Forward,AF)[6-7]协议和译码转发(Decode-and-Forward,DF)[8-9]协议最为常见。AF 协议指的是中继对接收到的信号不进行译码处理,仅进行信号放大处理;而DF 协议指的是中继对接收到的信号进行译码,恢复原始信号,然后重新编码后再发送出去。
在双向多中继系统中,受限于信道最差的中继,利用所有中继进行信息转发的方式不一定能够提高系统的性能[10]。中继选择技术通过在多个中继中选择一个或多个信道条件较好的中继转发信息,能够获得分集增益从而提高系统误比特率性能[11]。
中继的引入能够提高无线传输的可靠性,但同时也带来一些缺陷,如终端之间的协调、信号处理复杂度提高等,其中最为主要的是导致频带效率降低。为了弥补这一缺陷,基于无线通信中信号传输所具有的广播特性,网络编码[12-13]技术被引入无线协同通信中,用以提高无线协同通信系统的频带利用率[14]。网络编码典型的应用场景是双向中继网络,即一对通信终端通过中继完成信息交换。由于这种具有电磁波混合特性的网络编码方法涉及调制、解调与编译码等物理层技术,将其称为物理层网络编码(Physical-Layer Network Coding,PLNC),此外根据中继采用的协议不同(AF 或DF),又称为AF-PLNC 和DF-PLNC。
现在,人们越来越关注网络编码与其他技术的结合。Song 等在文献[15]中提出一种基于模拟网络编码的双向中继网络中的差分调制方法,理论分析和仿真结果表明,该文献提出的差分调制方法使得系统BER 性能提升了3 dB,若再引入功率分配,则系统性能还将再提升1~2 dB。
目前,OFDM 中继系统已经得到了广泛的研究。现有文献中提出将一些技术与OFDM 中继技术相结合,用以提高系统的数据速率和可靠性,这些技术除了传统的功率分配技术[16]和多中继选择技术,还包括子载波配对(Subcarriers Pairing,SP)[17-20]技术和子载波抑制(Subcarriers Suppression,SS)[2]技术。其中,子载波配对技术通常用于单向多跳OFDM 中继系统中,其核心思想为将相邻两跳之间的不同子载波按照一定准则进行配对,同一符号在配对的子载波间传输,用以提高可达速率。而子载波抑制技术则是一项非常具有实际应用前景的OFDM 技术,其核心思想是根据各个子载波的瞬时CSI,选择信道条件较好的子载波加载符号,进行信息传输,而将信道条件较差的子载波抑制掉,避免因为深衰落导致信道条件很差的子载波浪费过多功率,从而影响系统整体性能。文献[2]中的仿真结果表明,在OFDM 系统中引入SS 技术能在不影响吞吐量的前提下极大地提高系统的误比特率性能。文献[21]针对双向OFDM 中继系统,将SS 技术与SP 技术相结合,提出了一种联合子载波抑制-子载波配对(Subcarriers Pair based Subcarriers Suppression,SPSS)方案。相比于单纯的子载波抑制方案,SPSS能够取得更好的误码率性能。然而,文献[21]仅仅采用了简单的功率分配方法,并没有考虑针对误比特率性能进行功率优化。本文主要考虑基于SPSS 的双向OFDM 中继系统的功率分配优化问题,提出了基于本地信道状态信息(Channel State Information,CSI)的多址接入(Multiple Access,MA)阶段的次优功率分配策略和广播(Broadcast,BC)阶段的最优功率分配策略。在终端功率一定的条件下,通过优化各个终端不同子载波上加载的功率,达到减小系统误比特率的效果。通过对系统误比特率表达式进行分析,将功率优化问题分为两部分,并提出对应的方案。一部分是MA 阶段,针对两侧信源的功率分配问题,考虑已知本地CSI,提出了一种本地次优的功率分配优化算法;另一部分是BC 阶段,针对中继处的功率分配问题,提出了一种最优的功率分配优化算法。
本文结构安排如下:第1 节给出系统模型;第2 节简要描述文献[21]中提出的SPSS 技术;第3 节给出基于SPSS 的OFDM 双向中继系统的功率分配优化算法;第4 节给出数值仿真结果,并与传统方案进行对比;第5 节给出结论。
1 系统模型
在双向中继网络(Two Way Relay Network,TWRN)系统中,S1和S2通过中继R 进行信息交换,如图1 所示。系统采用时分多址(Time Division Multiple Access,TDMA)协议,信号传输可以分为两个阶段。第1个阶段为多址接入阶段,S1和S2同时向R 发送信号,R 进行译码转发处理;第2阶段为广播阶段,R 将处理后的信号广播给S1和S2,然后S1和S2进行译码,得到来自对方的信息。每个节点均采用OFDM 传输方式,子载波个数为K,每个子载波上的符号采用正交相移键控(Quadrature Phase Shift Keying,QPSK)调制方式。
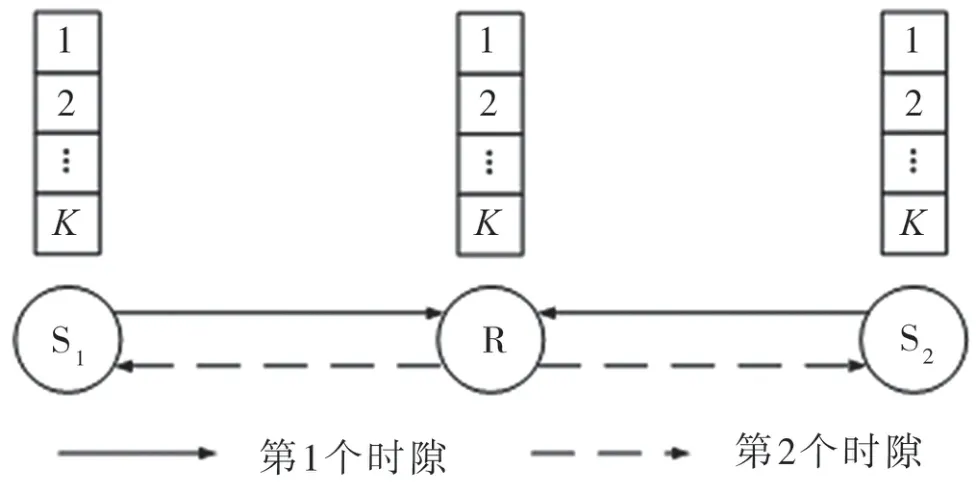
图1 双向OFDM 单中继系统模型
在多址接入阶段,节点Si(i=1,2)在第k个子载波上发送的基带信号可以表示为:

式中:ai,I[k]和ai,Q[k]分别为si[k]的同相分量和正交分量,且等概取±1。假设任意两个端点之间的时域信道服从于LL 径的瑞利衰落,且每一径的方差都相等,为1/LL。根据文献[19],当满足LL=K时,频域信号可以建模为服从均值为0,协方差矩阵为单位矩阵的环对称复高斯分布的随机向量。假设S1、S2和R 具有独立的功率约束,分别为P1,P2和PR,各个端点在子载波间进行功率分配。通过功率分配,中继R 在第k个子载波上的接收信号可以表示为:

式中:αi,k为Si(i=1,2)处第k个子载波分配的功率占节点总功率的比例。因而存在功率约束:

定义Hi[k]表示Si(i=1,2)与R 间第k个子载波的信道增益,nR[k]表示中继R 处第k个子载波上的噪声,且有nR[k]~CN(0,σn2)。假设所有端点均仅已知本地CSI,且CSI 在整个信息传输过程中(即MA阶段和BC 阶段)不改变。由于Si(i=1,2)已知其到R 之间的CSI,故可以采用相位补偿技术,使得到达R 的信息相角为0,即Hi[k]可视为实数。
当接收到来自S1和S2的混合信号后,R 对每一个子载波进行网络编码译码处理,判决规则为:

此时多址接入阶段(MA阶段)给定信道条件下,第k个子载波上的误比特率可以表示为:

式中:βk为R 处第k个子载波分配的功率占R 处总功率的比例;sR[k]表示中继R 处第k个子载波上的发送信号;ni[k]为Si(i=1,2)处第k个子载波上的噪声。sR[k]的计算式为:

式中:ni[k]为Si(i=1,2)处第k个子载波上的噪声。广播阶段S1和S2采用QPSK 译码方式,因而在给定信道条件下,广播阶段Si(i=1,2)处第k个子载波上的误比特率为:
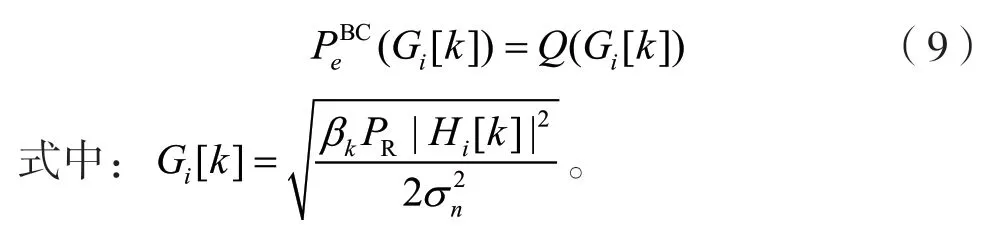
2 联合子载波抑制-子载波配对方法(SPSS)
文献[21]提出将子载波配对技术与子载波抑制技术相结合,其实现基础为文献[2]中的功率分配方式,称为信道反转,即发送端在不同子载波上加载的功率与子载波对应的CSI 模的平方成反比,从而使得每一个子载波上在接收端处的接收电平都相同,其表达式为:

广播阶段中,中继R 处仅采用简单的平均功率分配,即:
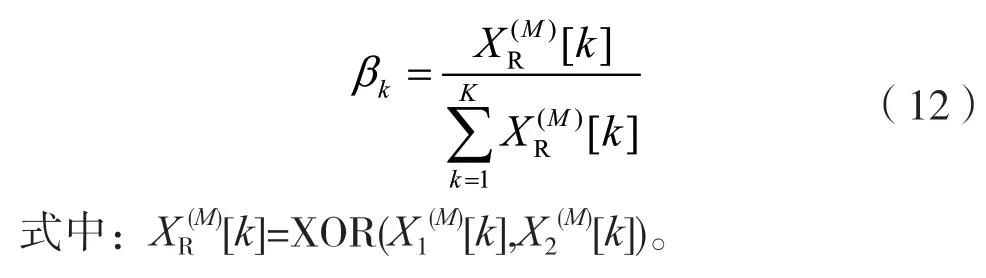
3 基于联合子载波配对与子载波抑制的功率优化分配
传统SPSS 方案中,功率分配仅仅采用简单的信道反转和平均分配的方式。这种方式实现简单,但是并不能获得很好的误比特率性能,因此,本文在SPSS 方案的基础上考虑功率优化分配。假设第1类子载波两侧子载波的集合为Ω1,第2 类子载波中右侧被抑制、左侧未被抑制的子载波集合为Ω21,第2 类子载波中左侧被抑制、右侧未被抑制的子载波集合为Ω22。此时,在信道条件固定的情况下,系统的误比特率可以表示为:

式中:π(·)表示子载波配对函数。式(13)可以化简为:

由式(14)可以看到,多址接入阶段和广播阶段的功率分配优化可以分开进行。
3.1 多址接入阶段功率分配
给定信道条件下,系统多址接入阶段的误比特率可以改写为:

由于S1与S2均只已知本地CSI,在此条件下给出本地次优功率分配算法,如下文所述。
首先考虑S1处功率分配,由于S1不知道S2和R 之间的信道向量H2,因此假设S2处功率平均分配,此时优化问题转化为:

由于目标函数是多个不连续函数和的形式,难以求得全局最优功率分配,因此考虑实现本地次优的功率分配,分配算法如下:

其中,

算法1 中步骤3 可以表示为以下优化问题:
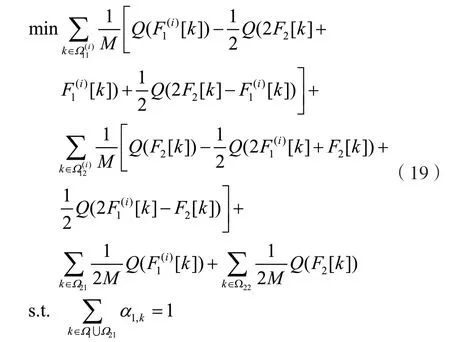
下一节采用拉格朗日对偶法进行求解。
3.1.1 问题建模
拉格朗日函数为:
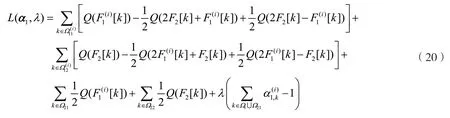
对偶函数为:

注意到对偶函数可分解,对偶函数可进一步等价为:

其中,

此时,对偶问题可以写为:

3.1.2 对偶子问题求解
对偶子问题为:
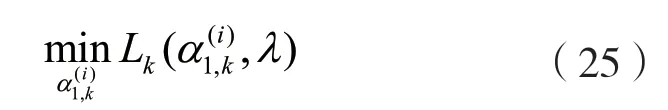
一阶最优性条件为:

3.1.3 对偶主问题的求解
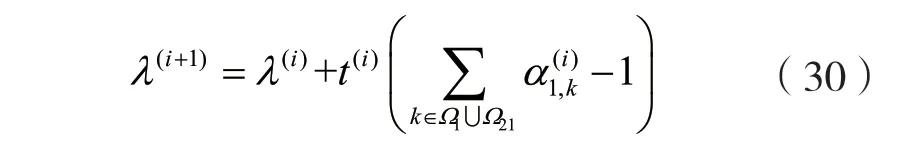
式中:t(i)是每次迭代的步长。次梯度算法可以保证收敛到最优值,通过足够多的迭代次数,可以得到近似最优值。
S2处功率分配方法与S1处相同,这里省略了步骤,优化问题可以表示如下:

3.2 广播阶段功率分配
给定信道条件下,系统广播阶段误比特率可以改写为:
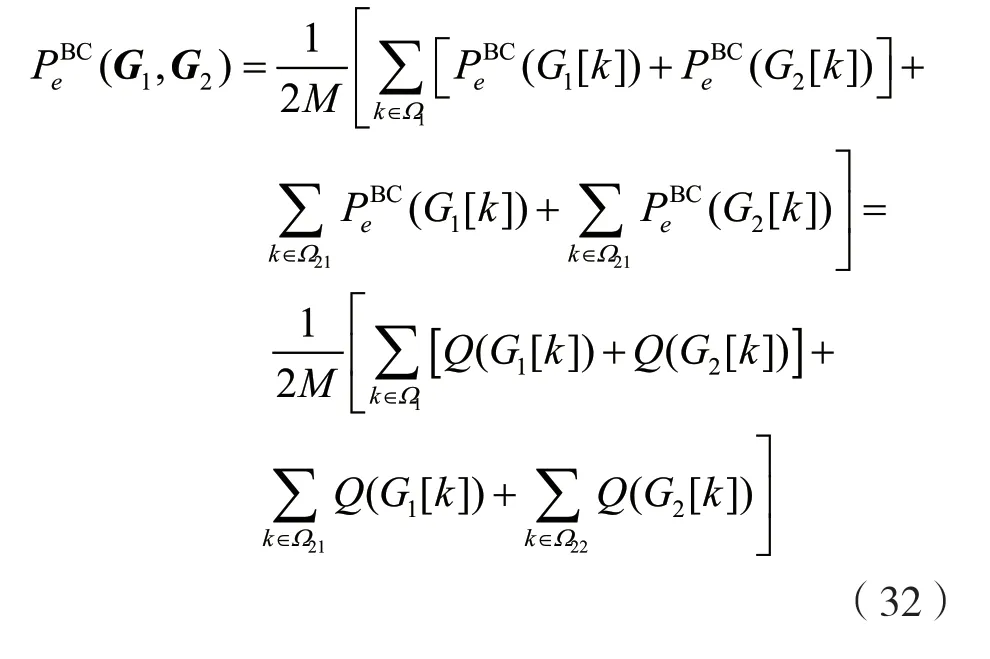
此时,优化问题可以表示为:

下面采用拉格朗日对偶法进行求解。
3.2.1 问题建模
拉格朗日函数为:
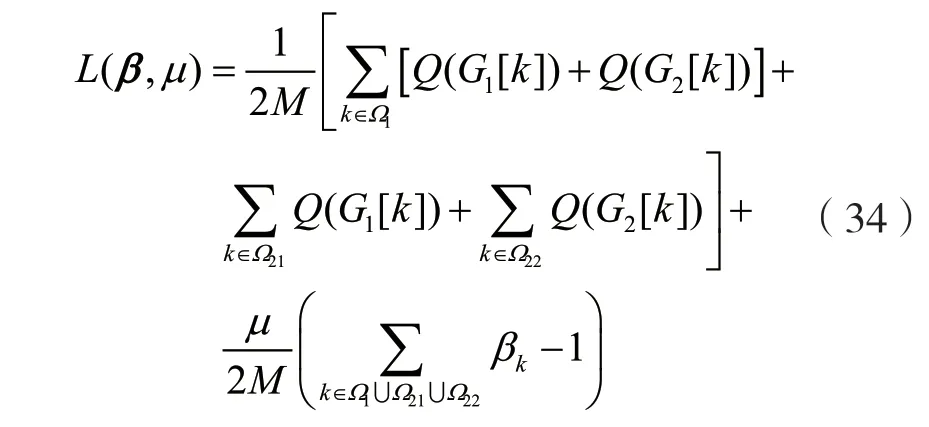
对偶函数为:
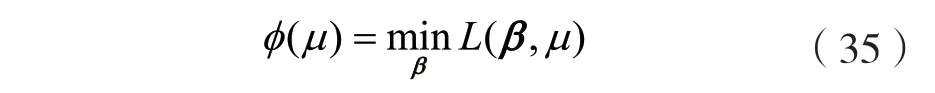
注意到对偶函数可分解,对偶函数可进一步等价为:

式中,

此时,对偶问题可以写为:
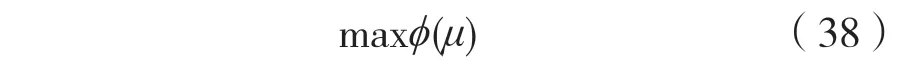
3.2.2 对偶子问题求解
对偶子问题为:

一阶最优性条件为:

当k∈Ω1时,有:
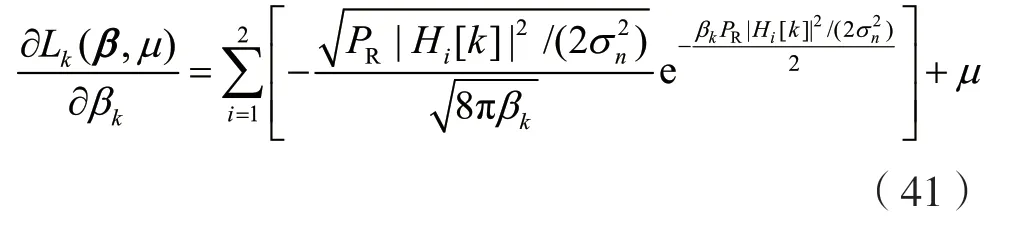
对应βk可由以下方程组得到:

3.2.3 对偶主问题的求解

式中:t(i)为每次迭代的步长。次梯度算法可以保证收敛到最优值,通过足够多的迭代次数,可以得到近似最优值。
4 仿真结果
本文利用计算机仿真检验所提功率分配方法的BER 性能,并与文献[21]所提的未使用功率优化的SPSS 方法进行比较。其中,对比策略1 为MA阶段和BC 阶段均采用平均功率分配;对比策略2为MA 阶段采用信道反转功率分配,BC 阶段采用平均分配;本文所提策略为MA 阶段采用本地次优功率分配,BC 阶段采用最优功率分配。假设所有节点的传输功率都设为1,子载波个数用K表示,M表示未被抑制的子载波个数。各子载波上均采用QPSK 调制方式。
图2 给出了基于JSPSS 的不同功率分配策略之间的BER 性能,其中,K=32,M=27。可以看到,本文所提策略在整个信噪比范围内的误比特率性能都优于现有的策略1 和策略2,整体上本文所提策略优于策略1 大约2 dB,优于策略2 大约1 dB。

图2 基于JSPSS 的不同功率分配策略的BER 性能对比
图3 比较了几种功率分配策略的BER 的值随平均未被抑制子载波个数M的变化曲线。图3 中,L=16,ρ=5,10,15 dB,M在32 到24 之间变化。从图中可以看出,当M逐渐减小时,几种分配策略的BER 均逐渐变小,策略1 与策略2 性能之间出现交叉,而本文所提策略则在不同M取值下都取得最优的BER 性能。因此,本文所提的功率分配优化策略在不同条件下都能够对BER 性能有很好的改善。

图3 几种子载波抑制方法随M 变化的曲线
5 结语
本文研究了基于JSPSS 的双向OFDM 中继系统的功率分配优化问题。分别提出了基于本地CSI 的多址接入阶段的次优功率分配策略和广播阶段的最优功率分配策略。仿真结果表明,与现有的功率分配策略相比,本文提出的功率分配策略能够带来误比特率性能的提升。
