基于CPS-SPWM策略控制的级联H桥逆变器研究

孙大伟,刘振兴

(1.宁夏电力能源科技有限公司，宁夏 银川 750011；2.华中科技大学，湖北 武汉 430074)

传统两电平逆变器拓扑结构在低压小功率电动机领域应用广泛，但随着大功率高压电力电子装置的快速发展，在中高压大容量电动机领域场合应用中，系统为输出更高质量的波形需要提高器件的开关频率或增大滤波电感，同时将会增大开关损耗，降低输电效率，提高装置成本等[1]。为此，有学者提出一种多电平功率变换技术，旨在解决功率开关耐压不足与高压大功率驱动之间的矛盾，并且可以有效降低输出电压的谐波含量，提高输出电能质量，降低能源浪费。

多电平逆变器经过各国学者的研究和改进，相继出现中性点钳位(NPC)[2]、飞跨电容(FC)[3]、级联H桥(CHB)型[4]等拓扑[5]。其中，CHB型逆变器由于结构简单，易于模块化实现、可冗余运行、输出波形质量高等优点[6]，成为多电平逆变器的研究热点，被广泛运用于光伏并网发电[7]、有源滤波器(APF)[8]、静止同步补偿器(STATCOM)[9]、电力电子变压器[10]、配电网接地故障消弧装置等不同场合中[11]。

脉宽调制技术(PWM)控制策略是多电平逆变器研究中的关键技术，该技术不仅可以体现出多电平逆变器的实现程度，而且直接影响输出波形的质量，系统损耗及输电效率[12]。在实现多电平逆变器功能时，不仅要搭建合适的电路拓扑结构，还需要响应的PWM控制策略作为保证，从而确保系统高效率高质量运行。随着CHB应用范围越来越广，对输出波形质量的要求越来越高，CPS-SPWM控制策略应运而生。

CPS-SPWM技术可以通过抵消低次谐波而非简单地将谐波推到高阶，以较低的开关频率器件等效实现更高的开关频率，具有良好的谐波性能。CPS-SPWM可以有效降低输出谐波，提高信号传输带宽，此外，还具有线性度高、控制功能突出等优点。由于SPWM具有多种调制方式，如单极性SPWM、双极性SPWM和单极性倍频SPWM，因此在此基础上产生多种CPS-SPWM方法。本文重点介绍基于单极性倍频SPWM的CPS-SPWM方法和基于双极性SPWM的CPS-SPWM方法。通过比较这两种方法，分析输出波形质量的影响因素。

1 CHB拓扑结构与工作原理

CHB逆变器的基本单元是一个单相全桥逆变电路，其拓扑结构如图 1所示。T1-T4为可控的电力电子开关器件(如IGBT、MOSFET等)[13]。

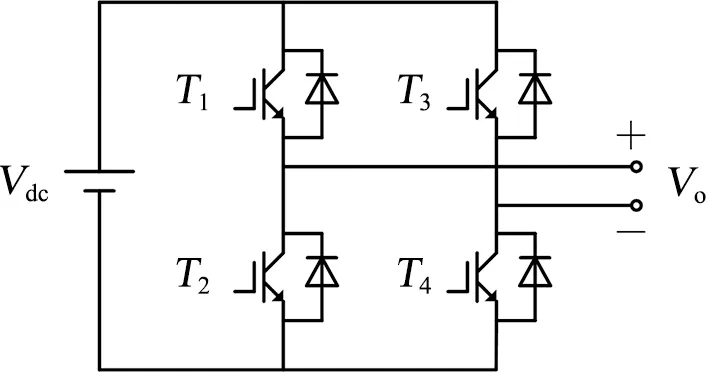
图1 单相全桥逆变电路

正常工作情况下，单相全桥逆变电路H桥单元中桥臂上下2个开关管互补导通，即T1与T2，T3与T4的驱动信号互补。假设直流电源输入恒定为Vdc，根据H桥中半导体功率器件开关状态不同，可以输出“Vdc”，“0”，“-Vdc”3种不同的电平。输出电平与半导体功率器件开关状态之间的关系为

Vo=(T1-T3)E

(1)

式中：Vo为H桥单元的输出电压；T1为表示对应开关器件关断，为1时表示导通，T3与T1类似。当T1、T3取值同时为0或1时，H桥单元输出0电平，因此具备冗余性，为系统的设计及控制提供灵活性。

通过改变开关器件的状态，从而控制交流侧输出电压。当各个电力电子开关导通组合不同时，输出电压Vo见表 1。

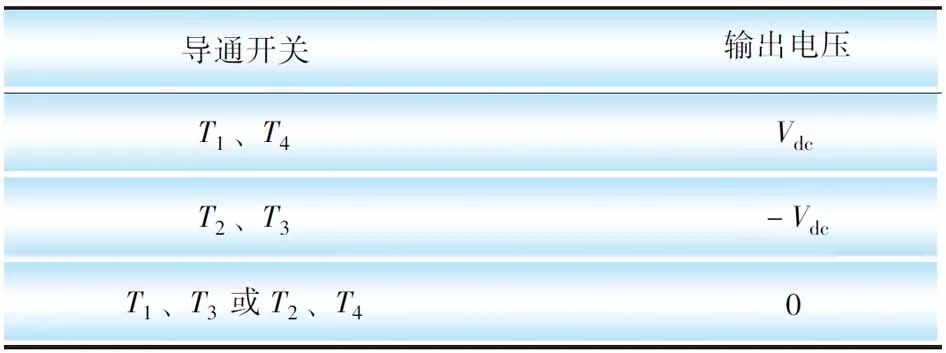
表1 开关组合及输出电压

级联型多电平逆变器则是通过多个单相全桥逆变器单元串联组成的单相或三相逆变器，如图2所示。每个逆变单元都可以输出阶梯波或方波，通过波形的合成叠加，形成更多电平的阶梯波，从而逼近正弦输出电压[14]。

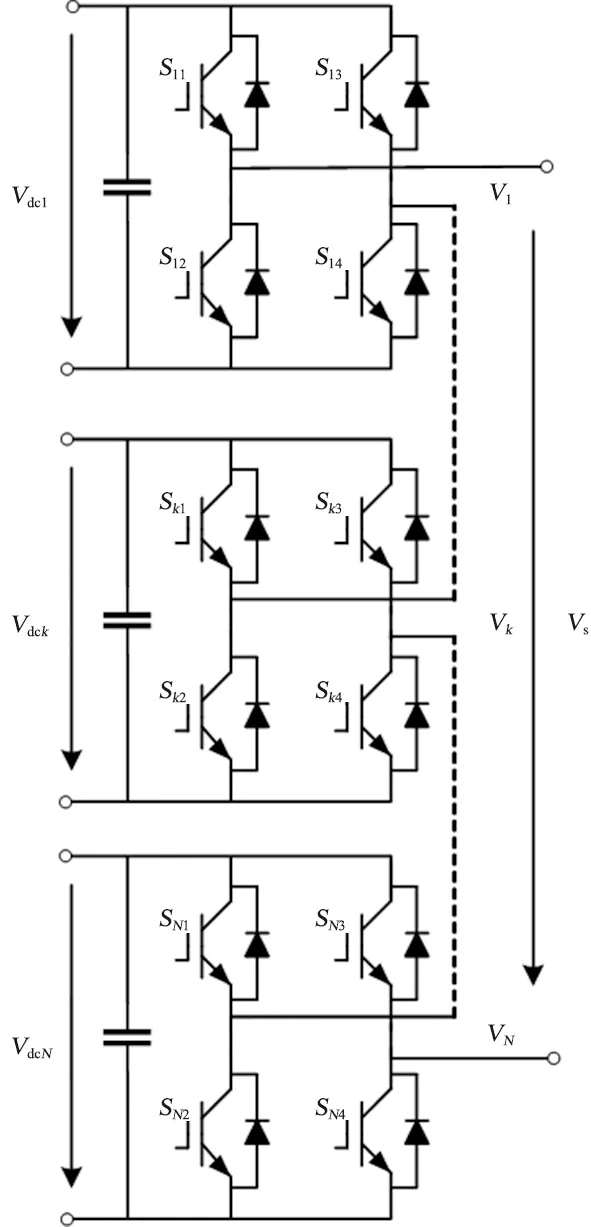
图2 单相级联H桥拓扑结构

2 理论分析

SPWM的基本思想是利用三角载波和正弦调制波的交点作为逆变器的开关控制信号。开关角控制由载波频率和调制度决定，而输出基波幅值与调制度呈线性关系。载波频率的变化只改变基波频率的分布中心，对各次谐波的幅值影响不大。

a.双极性SPWM

双极性SPWM的自然采样调制波如图3所示，双极性体现在输出电压在正负半周期内均有正脉冲和负脉冲。

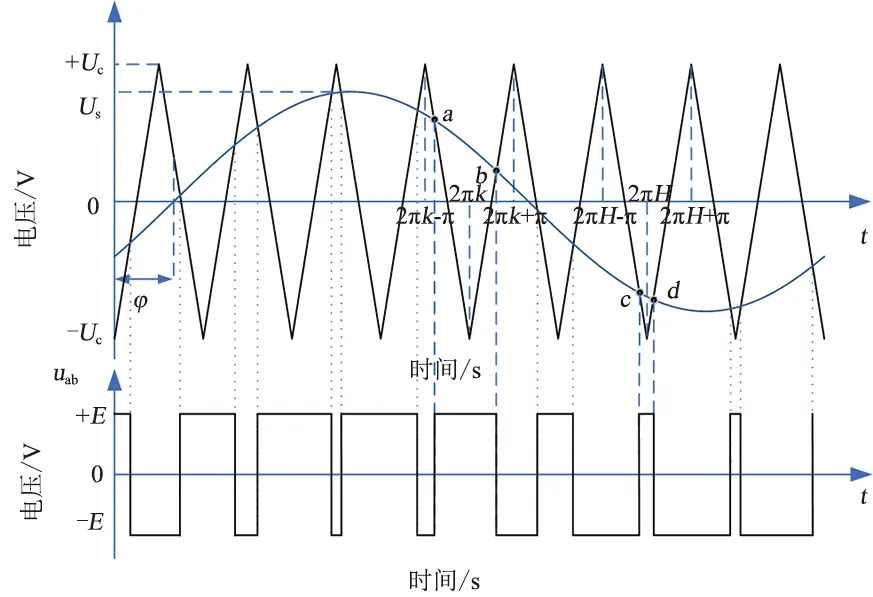
图3 双极性SPWM的调制

b.单极性倍频SPWM

输出电压的正半周期只有正脉冲，负半周期只有负脉冲，因此成为单极性倍频SPWM。单极性倍频SPWM可以使用相同的开关频率得到2倍的脉冲数，从而降低开关损耗，提高输出波形质量。调制方法如图4所示。

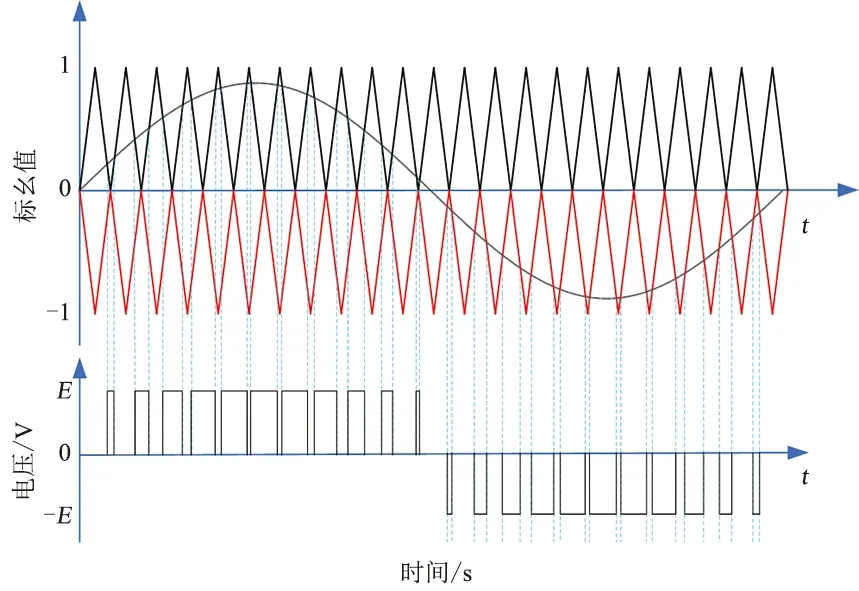
图4 单极性倍频SPWM调制

c.CPS-SPWM调制策略

载波移相正弦脉宽调制技术适用于大功率电力电子装置，是目前级联H桥逆变器较为成熟、运用较为广泛的调制策略。

以单相为例，CPS-SPWM的基本原理如下：在基本功率单元数量为N的级联H桥逆变器中，每个逆变器功率单元取共同的调制信号us(ωst)，其频率为ωs。每个逆变器功率单元对应的载波频率为kcωs，通过将每个三角载波的相位错开一定角度，级联H桥逆变器的输出电压将是多电平的。

双极性CPS-SPWM的原理是在上述基础上，将每个三角载波的相位错开1/N个三角载波周期，因此第L个逆变单元的相位为φL=φc+2πL/N。而单极倍频CPS-SPWM的原理是将三角载波的相位错开1/2N个三角载波周期，则第L个逆变单元的相位为φL=φc+πL/N。分别采用上述策略的逆变器输出电压分别为N+1个阶梯电平和2N+1个阶梯电平。

3 仿真分析

a.双极性CPS-SPWM

仿真参数如下：设H桥个数N=4，调频比kc=10，调幅比M=0.8。搭建Matlab/Simulink仿真模型后得到以下试验结果。

单相的调制波形如图 5所示，三相输出波形如图6所示。对输出波形进行快速傅里叶分析，如图7所示，分析可知谐波主要分布在40次谐波附近。

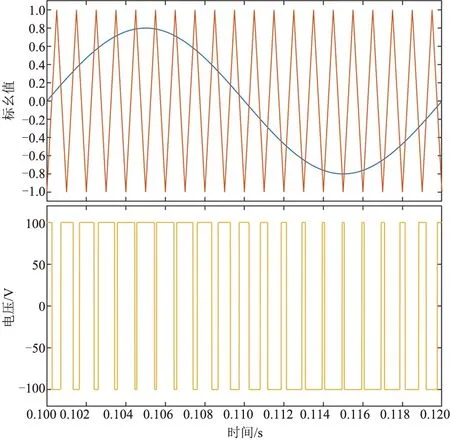
图5 双极性SPWM调制波形

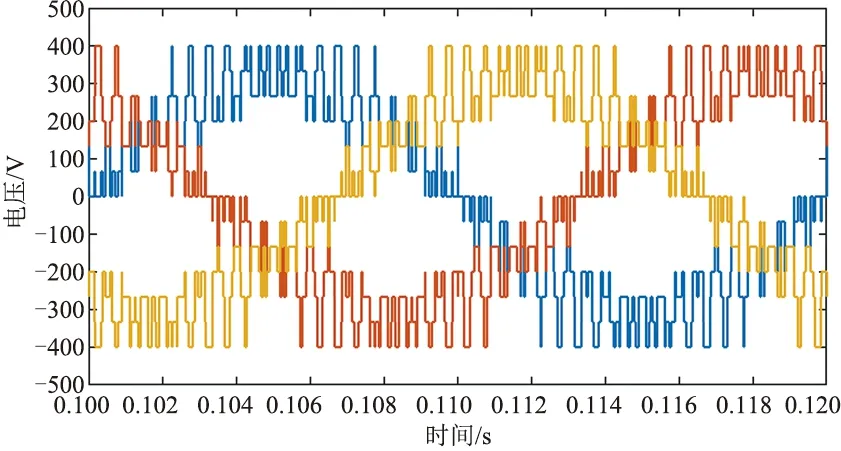
图6 双极性SPWM输出波形(kc=10)

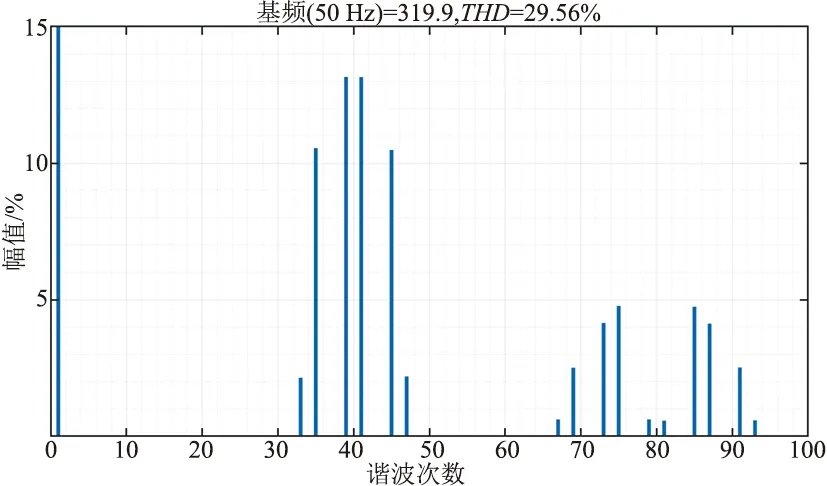
图7 双极性SPWM输出FFT分析(kc=10)

改变调频比kc=20，其输出波形与快速傅里叶分析如图8、图9所示，分析可知谐波主要分布在80次谐波附近。

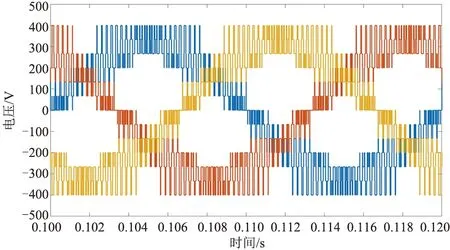
图8 双极性SPWM输出波形(kc=20)

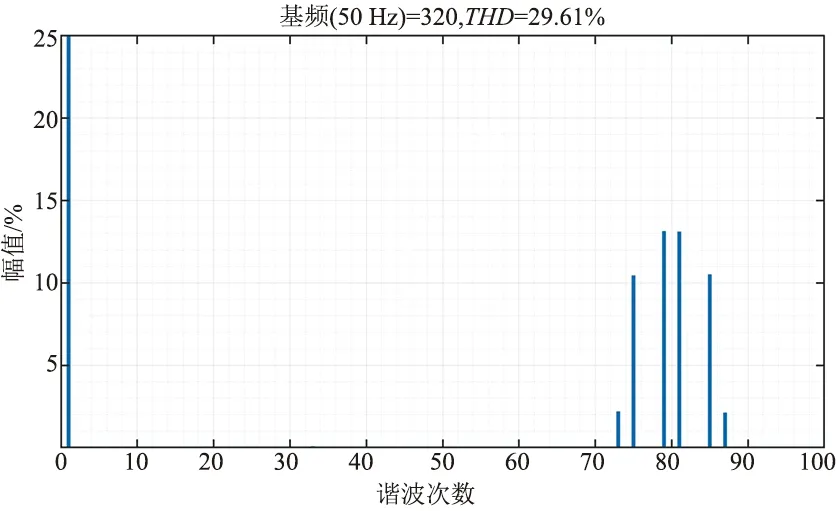
图9 双极性SPWM输出FFT分析(kc=20)

b.单极性倍频CPS-SPWM

仿真参数如下：设H桥个数N=4，调频比kc=10，调幅比M=0.8。搭建Matlab/Simulink仿真模型后得到以下结果：调制波形如图10所示，输出波形如图11所示。对输出波形进行快速傅里叶分析，如图12所示，分析可知谐波主要分布在80次谐波附近。

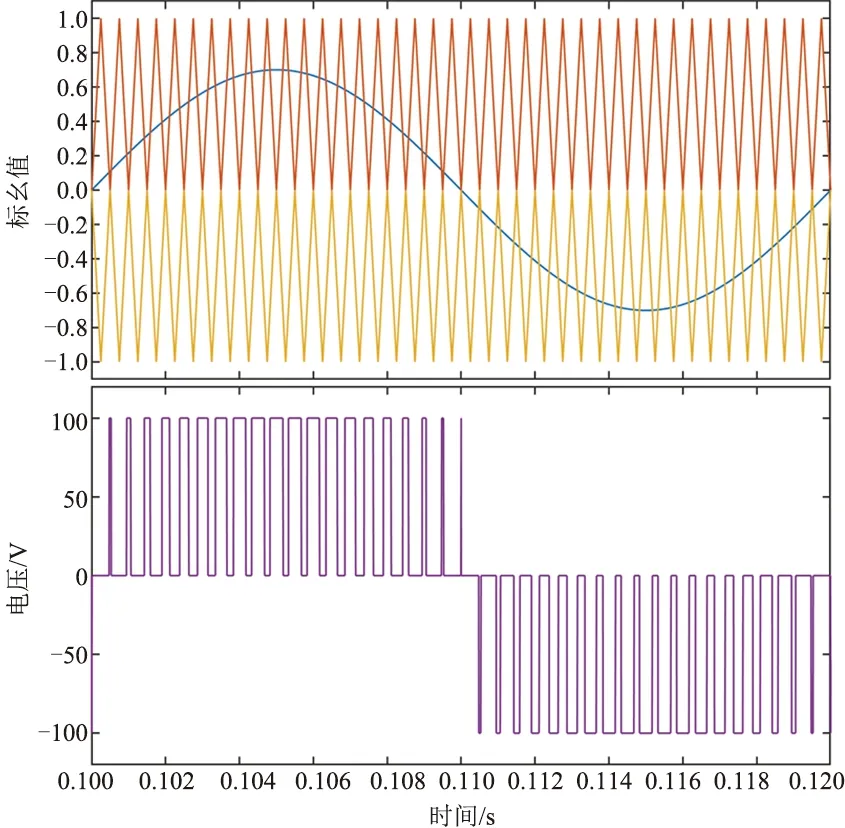
图10 单极性倍频SPWM调制波形

图11 单极性倍频SPWM输出波形(kc=10)

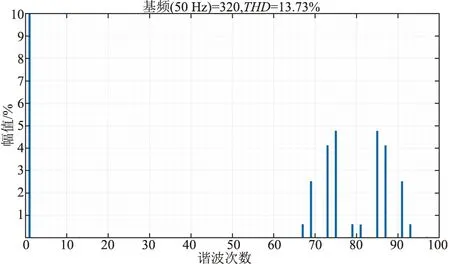
图12 单极性倍频SPWM FFT分析(kc=10)

改变调频比kc=20，其输出波形与快速傅里叶分析如图13、图14所示，分析可知谐波主要分布在160次谐波附近。

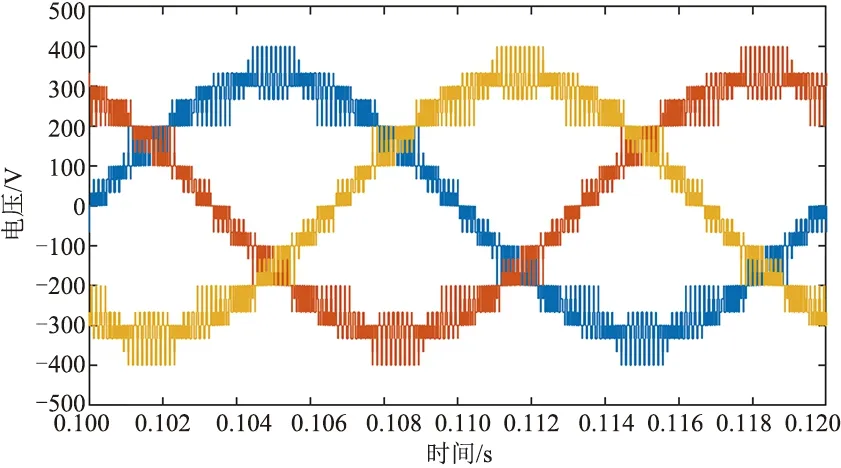
图13 单极性倍频SPWM输出波形(kc=20)

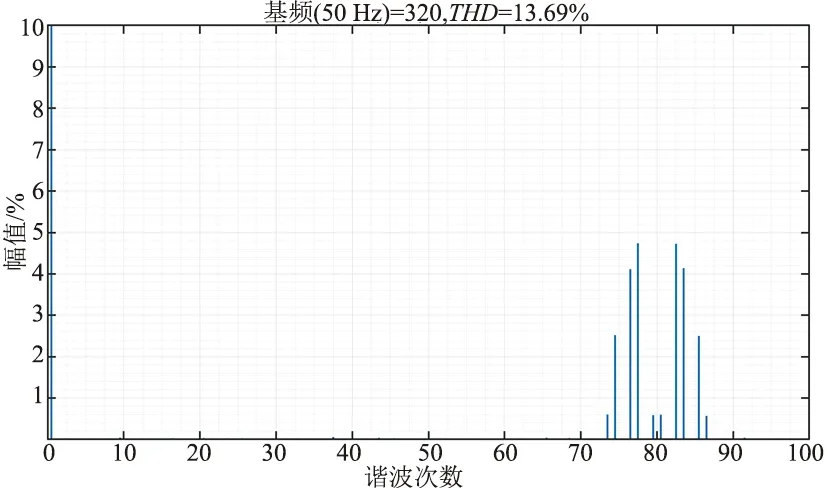
图14 单极性倍频SPWM FFT分析(kc=20)

c.综合分析

表2和表3分别列出4个H桥及等效开关频率为1000 Hz或4000 Hz条件下的仿真结果。比较双极性CPS-SPWM与单极性倍频CPS-SPWM结果，可知单极性倍频CPS-SPWM具有更高质量的输出电压，更少的谐波含量。

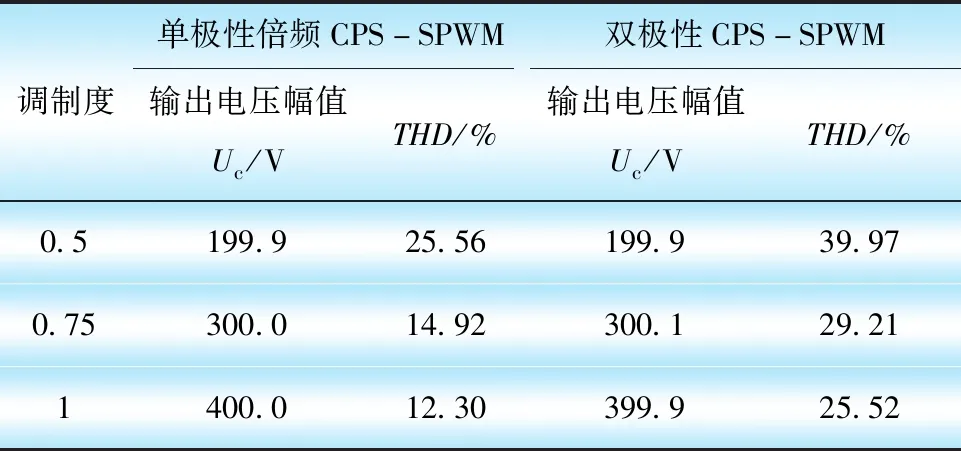
表2 等效开关频率为1000 Hz下比较

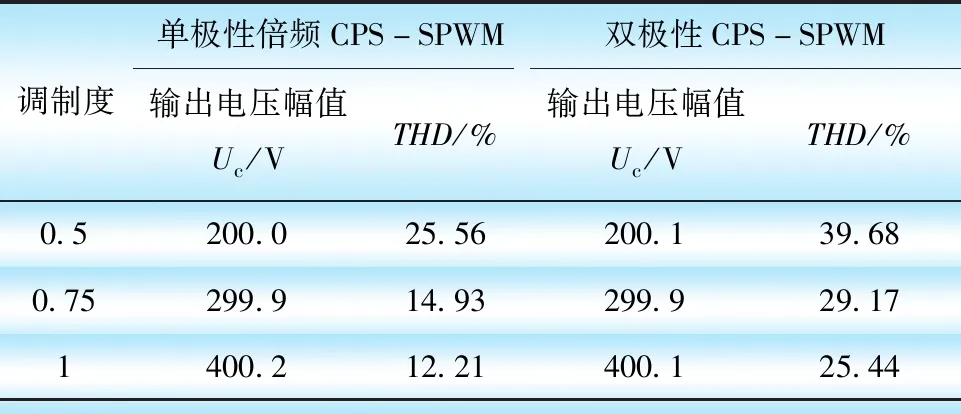
表3 等效开关频率为4000 Hz下比较

4 影响波形质量的因素

a.H桥数量

通过保持开关频率f=500 Hz、调制度M=0.8、直流电压为Udc，而只改变H桥的数量，对单相级联H桥分别采取上述2种调制策略，可以得到表4。

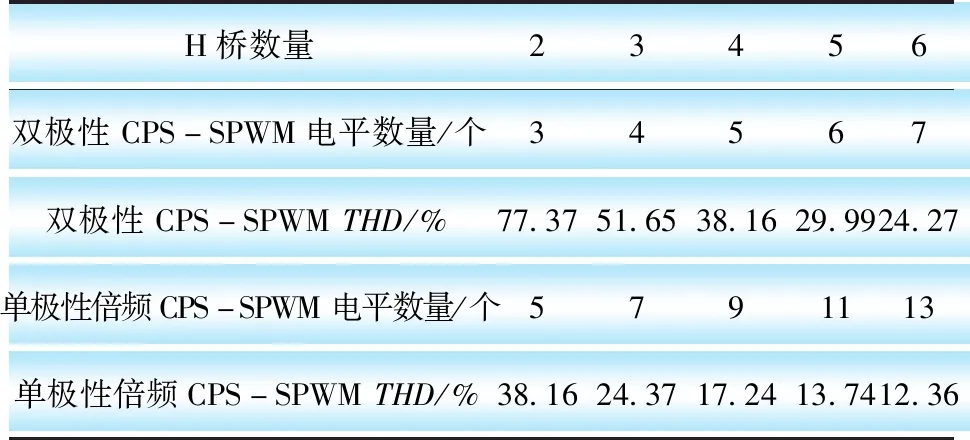
表4 不同H桥数量下2种策略的比较

由表4可知，双极性CPS-SPWM输出电平数量l=N+1，而单极性倍频CPS-SPWM输出电平数量l=2N+1；同时在相同的直流电压Udc下，H桥的数量越多，可以获得的输出电平越多，输出波形与正弦波就更为接近，谐波含量更少。然而实际H桥的数量不能无限增加，还需要考虑器件成本、输出谐波、输出电压电平等因素。

b.调制度M

在PWM控制策略中，调制度的变化将影响输出电压阶梯电平，从而影响输出谐波含量。

保持开关频率f=500 Hz、直流电压Udc=100 V、H桥数量N=4，对单相级联H桥逆变器分别采用双极性与单极倍频CPS-SPWM调制策略，通过改变调制度M的大小，得到表5。

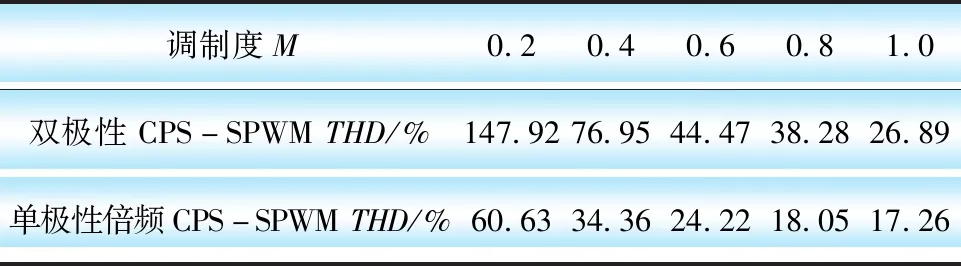
表5 不同调制度下2种策略的比较

由表5可知，调制度对于输出电压谐波含量也具有较大的影响作用，不过通过改变调幅比来提高输出波形质量的空间有限，因此控制合适的调制度可以有效降低总谐波失真度。

c.调频比

调频比主要影响的是输出电压的脉冲数，可以决定输出电压的谐波带分布情况。与调制比M一样，通过改变调频比来提高输出波形质量的空间有限。根据仿真波形图7、图9及图12、图14的对比可知，输出电压的波形可通过调整H桥的调频比来改善。因此，选择适当的幅度和频率调制比组合是提高输出波形质量的有效途径。

5 结语

仿真结果表明，单极性倍频CPS-SPWM策略比双极性CPS-SPWM策略更适合工业应用，并且最终输出波形质量受H桥数量、调制度、调频比等影响，但H桥数量的增加将提高硬件成本；调制度的增加也将提高两种策略的输出电压质量，但调制度还需要考虑工程对电压的需求；提高调频比也能提高输出电压质量，但调制空间有限，而且更高的调频比对载波发生模块有着更高的性能要求。因此需要变换器设计时对级联H桥逆变器的拓扑结构和参数进行正确选择。

CPS-SPWM调制策略对输出电压质量有着显著的提高，且基于CPS-SPWM调制策略的级联H桥逆变器不仅具有级联多电平拓扑结构的优点，如结构简单、便于模块化设计、级联单元之间相互独立等，同时还具有CPS-SPWM的优点，在低开关频率下等效实现高开关频率的效果。所以基于CPS-SPWM的级联H桥逆变器可以大大提高逆变器的应用性能。