人行悬索桥人致振动舒适度分析与试验研究

方建华，武芳文，谢 亮，秦 枭，冯彦鹏

(1.绍兴市轨道交通集团有限公司，浙江 绍兴 312000；2.长安大学 公路学院，陕西 西安 710064)

0 引言

近年来，我国建设了大量的人行桥，随着工程建造能力提高和对景观美学的追求，工程师们将轻质高强材料应用到了人行桥的建造中。该类人行桥与传统的混凝土结构相比，结构更加轻盈，结构振动频率较低，在行人以正常的步行速度行走时容易产生较大的振动响应。

国内外众多学者都进行了人行桥人致振动的研究。在人行荷载的测量方面，ANDRIACCHI等[1]采用测力板测试人行荷载在竖向、横向和纵向3个方向上的分量，并且绘制3个方向上步行力曲线。在步行参数方面，陈政清等[2]采用摄像机观测学生的步行特征，统计了学生的步频和步长，统计结果表明行人的步频和步长均符合正态分布。在人行荷载模拟方面，BROWNJOHN、MATSUMOTO、BACHMAN等[3-5]从多种角度提出了不同的人行荷载模型，孙利民等[6]通过试验和理论研究得出了人行荷载的计算公式。目前，世界上许多国家的规范[7-9]都给出了人行荷载模型，并且给出了使用规定。

在人致振动响应分析方面，DALLARD等[10]对千禧桥进行了实测，提出了一种在人群密度较大时的横向振动响应计算方法；袁旭斌[11]推导了考虑人群同步概率的加速度共振响应计算公式；李红利等[12]提出了一种考虑随机性的步行力荷载模型，并且基于模态分析方法建立了一种人致振动响应计算方法；谢旭等[13]验证双腿支承人体荷载模型的计算精度，提出了一种考虑人-桥耦合效应的计算方法；张琼等[14]分析了随机人群的各种参数对结构振动加速度响应峰值的影响；操礼林[15]考虑了行走人群中的个体特性，建立了一种考虑人-桥相互作用的人致振动响应分析方法。

对于人行悬索桥而言，轻质的主梁和简单的约束条件使得结构十分轻柔，其自振频率与行人正常行走频率趋近，容易出现人致振动问题。另外，目前人行桥振动舒适度研究主要集中在中小跨径人行桥的研究上，针对大跨度人行悬索桥研究较少，也缺乏相应的试验研究，我国也尚未对人行悬索桥编制专门的设计规范。因此，开展人行悬索桥人致振动舒适度的研究具有重要意义。为此，本文以陕北某景区人行悬索桥为依托，采用了理论计算和现场实测的方法进行了人行悬索桥人致振动舒适度的研究。

1 人致振动响应分析方法

1.1 人群荷载模型

自千禧桥事件[16]后，多国的学者开展了人致振动的研究，相应的提出了许多用于分析的人群荷载模型。欧洲各国陆续颁布了其本国的人行桥设计规范，给出了适用于工程动力设计的人群荷载模型。在这些规范中，应用最为普遍的是ISO标准ISO 10137和德国EN03规范。ISO标准ISO 10137和德国EN03规范所给出的人群荷载计算模式差异较大，但都认为人致振动响应只要是由步频一致的人群所引起的。

中国城市人行天桥与人行地道技术规范CJJ/69(简称中国规范CJJ/69)中也给出了用于人行桥动力分析的人群荷载模型和计算方法。有研究表明，中国人和欧美人的步态参数存在一定的差异。因此，为了更贴近实际，采用中国规范CJJ/69的计算模式进行分析。中国规范CJJ/69中采用的谐波荷载p(t)，其表达式为：

(1)

式中：P为单个行人以步频fs行走产生的力的分量，竖向取值为280 N、横向取值为35 N；fs为步行频率，一般取值为人行桥的固有频率；n′为加载面积为S上的行人流等效人数，其计算如式(2)所示；S是桥面面积；ψ为行走步频接近结构基频的概率折减系数，其计算如图1所示。

(a)竖向折减系数

(2)

其中，ξ为结构的阻尼比；n为桥面上行人总数。

1.2 人致振动响应分析方法

人行桥在规范指定的人群荷载作用下的结构动力响应分析，可按如下步骤进行：①建立人行悬索桥全桥模型，分析结构动力特性，计算固有频率，并根据规范筛选出需要验算的敏感频率；②依据设计行人交通量和桥梁实际运营情况，确定合适的交通工况和行人密度；③拟定结构阻尼比；④根据敏感模态的振动特性，按照最不利的方式将谐波荷载加到结构上进行计算，如图2所示，得出加速度响应峰值。

图2 按模态振动特性施加谐波荷载

1.3 舒适度评价

人行桥的舒适度评价方法一般有两种，避开敏感频率法和限制结构动力响应值法。避开敏感频率法是要求人行桥的固有频率避开规范规定的敏感频率范围，这样在很大程度上能够避免出现人-桥共振现象，结构就不会发生较大的振动。然而，就目前的人行桥发展趋势而言，采用这种方法是不现实的，因为目前修建的人行桥，尤其是大跨度人行桥，若要避开敏感频率将需要大幅度提高结构的刚度，这将严重影响人行桥的经济性和美观性。因此，实际中多采用限制结构动力响应法，即人行桥在人群荷载作用下结构的加速度响应峰值小于规范规定值。目前，许多国家都将加速度响应峰值作为舒适度评价指标，例如英国、瑞典和德国等国家，各国规定加速度响应指标如表1。2017年，中国新颁布的《城市人行天桥与人行地道技术规范》也采用了限值结构动力响应的方法，并给出了如图3所示的舒适度限值曲线。

表1 各国规范舒适度评价标准Table 1 Comfort evaluation standards of national norm各国规范竖向加速度限值/(m·s-2)横向加速度限值/(m·s-2)英国规范BS 54000.5 f无瑞典规范Bro 20040.5无欧盟规范EN 19900.70.2德国规范EN 030.50.1

(a)竖向加速度限值曲线

从表1和图3中可以看出，中国规范指定的加速度限值较为严格，因为当结构自振频率小于2.5 Hz范围内时，即处于行人正常步频范围内，中国规范规定的加速度限值小于0.5 m/s2。本文中所描述的人行悬索桥跨度较大，结构十分轻柔，对控制人致振动响应的要求较高，因此按中国规范CJJ/69的舒适度限值曲线评价舒适度。

2 人致振动响应计算

2.1 悬索桥概况

人行悬索桥位于陕北某景区，桥面跨度200 m，桥面有效宽度为4 m，主缆的跨度布置为60 m+208.8 m+64 m。主缆成桥状态下垂度23.2 m，矢跨比1∶9，主缆采用抗拉强度为1 670 MPa 的平行钢丝，其等效直径为103 mm；吊索采用抗拉强度为1 860 MPa的整体式钢绞线，吊索纵向布置间距为3 m；加劲梁采用Q345格构式结构；桥塔结构形式为倾斜式混凝土拱塔；主梁两侧设置了抗风缆以抵抗风荷载，风缆平面与水平面成30°角。桥型布置和现场实况如图4所示。

(a)立面布置图

2.2 结构动力特性

采用ANSYS软件建立有限元模型分析了结构的动力特性，有限元模型如图5所示。其中主缆、吊索、抗风主缆和拉索均采用LINK10单元模拟，主梁、桥塔和承台采用梁单元模拟。约束条件为：①主缆锚碇处、承台底部和抗风缆锚碇处采用固结处理；②主缆在索鞍处释放掉沿桥梁纵轴方向的位移约束；③加劲梁两端共设置4处约束，只在其中一处设置纵向位移约束。

图5 有限元模型图

根据规范，拟定0.4%为结构的阻尼比，根据中国规范CJJ/69的规定，竖向自振频率小于3 Hz和横向自振频率处于0.5～1.2 Hz的模态都需要验算，其中需要重点验算的模态(荷载折减系数较高)如表2，部分振动模态图6所示。

表2 需要验算的模态特性值Table 2 Modal characteristic values to be checked模态阶数周期/s频率/Hz振型描述101.342 0.745横弯130.942 1.062160.647 1.545170.556 1.798180.501 1.998竖弯190.456 2.194200.409 2.443

(a)第10阶振型

2.3 人致振动响应

在进行人致振动响应分析之前应当选择合适的工况，根据人行桥的设计使用状况，该人行悬索桥设计人群密度为0.5人/m2，但由于该人行悬索桥位于陕北著名景区，在节假日营业期间可能会出现游客数量暴增的情况，故选取0.7 人/m2作为人群密度最大的工况进行计算。

需要重点说明的是，人行桥的实际振动是十分复杂的，其振动往往不是单阶模态振动，而是多阶模态振动的组合。然而，由于人行悬索桥结构轻柔，结构自振较低，有多阶结构自振频率处于行人正常行走步频范围内，所以组合振动的方式相当多，计算十分不便。因此，本桥的人致振动响应计算按照中国规范CJJ/69所推荐的方式，即假设人群的正常行走步频与对应的敏感频率一致，行人行走时人与桥发生共振，以此时的振动响应峰值作为加速度响应的计算值。该方法考虑的情形与实际情况存在一定的偏差，但这种加载方式保证了人桥共振必然发生，其计算值偏大，但更为安全。

据此，按照中国规范CJJ/69所规定的人群荷载的取值大小和加载方式，计算出了该人行悬索桥敏感模态下的加速度响应峰值，如表3所示。

表3 人致振动加速度响应峰值Table 3 Peak value of human induced vibration acceleration respone模态阶数结构频率/Hz振型描述加速度响应峰值/(m·s-2)1/4 L位置跨中位置加速度限值/(m·s-2)100.745横向0.1140.1440.1131.0620.0020.0370.1161.5451.3621.6140.345171.7981.6640.1210.394181.998竖向1.3062.0040.428192.1941.7110.1310.461202.4431.3141.7760.50

从横向振动响应结果可以看出，第10阶模态所对应的加速度相应峰值最大，其值已经大于0.1 m/s2。在竖向振动响应结果中，第16阶～第20阶模态对应的加速度响应值都较大，其中竖向加速度响应的最大值在第18阶对应的跨中位置取的是2.004 m/s2。

3 现场实测

人行悬索桥的振动响应与结构的模态参数有关，而实际结构的模态参数与有限元计算分析值可能会有较大差距，因此，为了分析人行悬索桥的动力特性与在人行荷载下的动力响应，分别对人行悬索桥进行了结构动力特性试验和人致振动试验。

3.1 结构动力特性试验

结构动力特性试验采用环境激励的方法进行。环境激励法即利用环境中的随机作用(如风荷载)对该结构进行激励从而产生振动，从振动响应中提取出衰减信号进行模态参数识别。试验仪器主要包括10个灵敏度为0.3 v/m/s2的磁电式多功能传感器、一台16通道的数字采集仪、一套三轴加速度传感器。在进行环境激励测试时，由于传感器数量较为有限且桥面较长，故采用分批次多次测量的方式测试结构的振动模态。环境激励测试的测点布置见图7，每次测试将传感器分成3组，每组4个，分别将其等间距布置在X方向50 m的范围内，在该组测试完成后，以距离5号塔最远的那组仪器作为参考点，移动前面两组仪器，进行下一组测试。其步骤如下：①分别设置1、2和3个参考点。每一组参考点可关联与之相关的前后两组测试，这样就能测得较为精确的振型数据。②采集数据。每一组进行3次测试，每次测试的采集时间为10 min。③移动测点。在一组测试完成之后，保持参考点位置处的4个传感器不动，移动另外8个传感器到下一组测点位置，进行下一组测试。重复以上所有操作，直至4组测试全部完成。

3.2 人致振动试验

人致振动试验将12个传感器布置在桥面的1/4L、1/2L和3/4L这3个具有代表性的位置处，即图7中参考点1、2和3的位置处。

(a)测点布置

人致振动试验主要分为两部分，跳跃激励测试和行人激励测试。跳跃激励测试主要目的也是为了进行参数识别，通过采集跳跃激励所得到的自由振动衰减曲线进行分析，从而获取模态参数，尤其是阻尼比。本次试验一共组织了两组跳跃激励测试，一组是单人在跨中跳跃测试，另一组是3人跨中跳跃测试，每一组分别采集5次跳跃振动响应数据。

行人激励测试主要是多人行走激励测试。试验中为了研究人数和行走步频对人行悬索桥振动响应的影响，选取了多个人群密度和步频进行试验。由于该桥结构十分轻柔，在人群密度达到0.5 人/m2时，结构会出现巨大的振动，可能会影响结构安全，所以试验选取了0.7 人/m2作为最大人群密度。另外，桥面有效宽度达到了4 m，行人行走情形多样，所以在多人行走激励测试中除了研究人数和行走步频对人行悬索桥振动响应的影响外，还进行了多种行走方式的测试，如图8所示。图8中展示了多种行走激励测试的行走方式，包括中线行走、边线行走、双线同向行走和双线反向行走。人群激励测试工况信息如表4。

图8 现场行走方式测试

表4 人群荷载激励测试工况Table 4 Crowd load excitation test conditions工况步频/Hz行人密度/(人·m-2)等效人数行走情形11.6、1.8、2.0、2.20.1255中线行走21.6、1.8、2.0、2.20.28中线行走31.6、1.8、2.0、2.20.513中线行走41.6、1.8、2.0、2.20.716中线行走51.6、1.8、2.0、2.20.716边线行走61.6、1.8、2.0、2.20.716双线同向行走71.6、1.8、2.0、2.20.716双线反向行走

4 实测结果分析

4.1 模态参数识别

试验进行了多组环境激励测试，其中某一次跨中4个测点的振动加速度响应如图9所示。针对试验中采集到的振动响应结果，本文采用频域的方法，将采集到的加速度响应信号进行快速傅里叶变换(FFT变换)，分别计算出其功率谱密度，取其均值作为振动频率。

图9 人行桥环境激励响应

采用解析模态分解法对跳跃激励测试中采集到的多条自由振动衰减曲线进行分析，其中一条衰减曲线如图10所示。将采集到的典型加速度响应曲线进行简单处理，然后利用模态分解法得到各阶单模态响应曲线，即可求出各阶模态的阻尼比。其中第3阶模态响应曲线如图11所示。

图10 跳跃激励响应曲线

图11 第3阶模态响应曲线

实测得到的较为重要的模态频率和阻尼比如表5所示。

表5 实测结构模态参数Table 5 Measured structural modal parameters阶数频率/Hz振型描述阻尼比/%100.79横弯0.33131.11横弯0.29161.49竖弯0.25171.83竖弯0.18182.01竖弯0.24192.22竖弯0.13202.48竖弯0.14

由表5可知，实测结构各阶模态的平均阻尼比为0.24%，说明结构的阻尼整体偏小，与规范给定的参考值有一定差别。

实测结构频率整体上略大于有限元分析值，综合现场实际情况分析，业主出于景观需求在主梁跨中位置附近安装了装饰和LED屏幕等设施(如图12所示)，这些设施的安装对结构的动力特性产生了影响。为探究附属设施对结构动力特性的影响，通过Mass21单元和Combin14单元组合的方式模拟附属设施，将每一块LED面板的质量集中于M0，通过弹簧刚度K0模拟附属设施与结构的连接(如图13所示)，然后进行动力分析，分析结果表6所示。

图12 爆裂效果LED屏幕安装

图13 附属设施模拟示意图

从表6可知，附属设施集中布置在跨中附近一定程度上改变了结构的动力特性：①附属设施作为结构附属质量单元增大了结构的自振频率；②附属设施的存在对结构动力特性有一定影响，但影响相对有限。

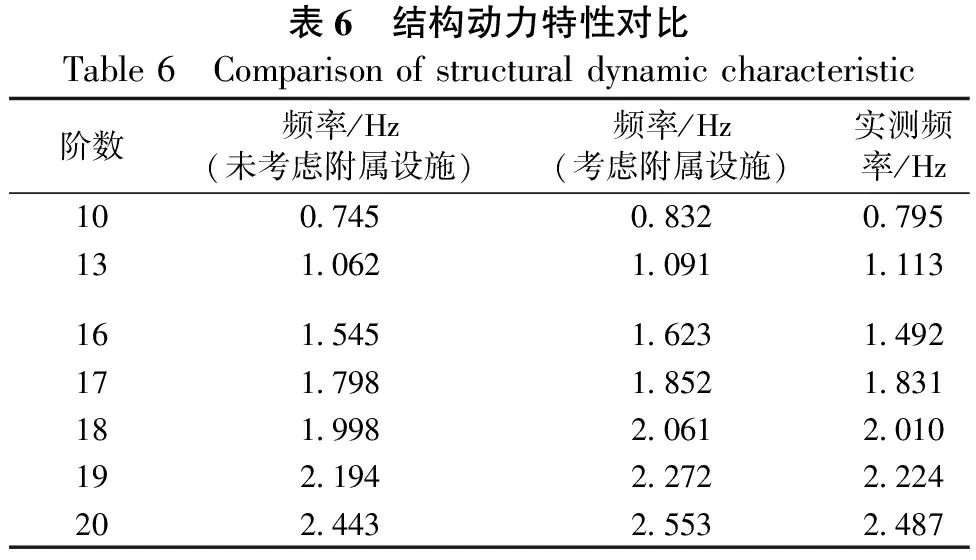
表6 结构动力特性对比Table 6 Comparison of structural dynamic characteristic阶数频率/Hz(未考虑附属设施)频率/Hz(考虑附属设施)实测频率/Hz100.7450.8320.795131.0621.0911.113161.5451.6231.492171.7981.8521.831181.9982.0612.010192.1942.2722.224202.4432.5532.487

4.2 人群激励下结构振动响应

4.2.1竖向与横向加速度响应

在多组人致振动试验中，得到了多组加速度响应时程曲线，其中人群在桥上行走所引起的最大竖向和横向加速度响应响应峰值分别为0.526 m/s2和横向加速度峰值为0.038 m/s2。从竖向和横向加速度响应对比可知，横向振动加速度响应峰值只有竖向加速度响应峰值的1/10左右，横向振动响应相当小。因此，该桥在实际行走过程中，可能会出现横向振动较小，但竖向振动已经超过了舒适度限值的情况。

4.2.2行走人数和步频对结构振动响应的影响

为研究行走人数和行走步频对人行悬索桥振动响应的影响，分别让不同行人密度的人群以不同的步频从桥面一端走向另一端。试验中每一工况都进行了多次测试，由于该桥的横向加速度响应相较于竖向加速度响应要小得多，所以仅统计了各工况下人行悬索桥的竖向加速度响应峰值，如表7所示。

表7 各工况下结构加速度峰值Table 7 Peak value of structural acceleration under different test conditions行人密度/(人·m-2)1.6/Hz1.8/Hz2.0/Hz2.2/Hz0.1250.1550.1870.2240.1760.20.2060.2420.2330.2770.50.2550.3450.4160.3980.70.3080.4230.4780.526

为分析行走步频和行人密度对竖向加速度响应峰值的影响，绘制了如图14所示曲线。从图中可以看出，当行人密度在不超过0.7 人/m2时，随着行人密度的增大，人行悬索桥的竖向加速度响应峰值基本呈线形增长，增长速率跟行走步频与结构自振频率的接近程度有关，1.8、2.0和2.2 Hz这3个步频均靠近该人行悬索桥的竖向自振频率，共振效应明显，所以振动响应比1.6 Hz更大。

图14 人群步行加速度响应峰值响应曲线

将实测值与前面有限元分析值结合来看，有限元计算的最大人致振动响应值为2.004 m/s2，已经远远超过了规范规定的限值，而实测的人致振动响应峰值也超过了中国规范CJJ/69规定的限值，这进一步验证了人行悬索桥人致振动问题突出的情况。

4.2.3行走方式对结构振动响应的影响

为研究行走方式对结构振动响应的影响，分别让人群以多种行走方式。试验进行了多组测试，其中一组测试所得加速度响应如图15所示。试验还统计了不同行走步频下各种行走方式所引起的加速度响应峰值分布，如图16所示。

单列中线行走和边线行走的加速度响应峰值和均方根值分别为0.425、0.147和0.436、0.159 m/s2，结合加速度响应时程曲线，说明行走时横向位置对该桥振动响应影响较小。双线同向行走和反向行走产生的加速度响应峰值和均方根值分别为0.526、0.183和0.389、0.117 m/s2，结合图15和图16可知，两列同向行走增加了人桥同步的概率，提高了结构的振动响应；而两列反向行走则恰好相反，该行走方式使人群分散，减弱了共振效应，导致结构的振动响应值减小。

(a)双线同向行走

图16 加速度响应峰值分布图

4.3 舒适度评价

根据现场实测结果，最大的竖向加速度响应值为0.529 m/s2，已经超过了最大限值0.462 m/s2的要求；最大横向加速度响应值未超过0.1 m/s2。在完成现场测试工作之后，对试验参加人员进行舒适度感受统计，大部分人员觉得在行人密度达到0.2 人/m2，已经能够明显的感受到结构的振动；当行人密度达到0.5人/m2时，有接近半数的人出现了不适感；当行人密度达到0.7 人/m2时，大多数人都出现了不适感。

在本次试验中，测试得到的最大竖向加速度响应已经超过了规范规定的舒适度限值，结合有限元分析结果，该人行悬索桥的竖向振动响应已经达到了相当大的水平，通过常规的措施很难控制其振动响应。除此之外，由于该桥为采用玻璃桥面的人行悬索桥，游客在桥上可以看到深谷，如果出现舒适度问题，可能会引发恐慌，从而导致安全事故，因此建议采用TMD阻尼器控制其竖向振动，将竖向的振动响应控制在一个较小的值以下。

5 振动控制

由4.3节舒适度评价可知，当该人行悬索桥上的行人密度达到设计状况时，其竖向振动加速度过了规范要求，由于该桥结构轻柔，且采用玻璃桥面，容易出现舒适度问题。因此，有必要采取一定方法措施对该人行桥进行振动控制。目前常用的振动控制方法有两类，分别是提高结构自振频率和增大结构阻尼。提高结构自振频率的方法简单可行，但这样做将显著的增大结构自重，这样的方法不满足人行悬索桥的景观需求。所以，增大结构阻尼是目前人行桥振动控制的常用且有效的方法。

目前增加结构阻尼的常用方法是安装阻尼器，阻尼器种类繁多，原理和用途也不尽相同，目前在人行桥振动控制领域，是调谐质量阻尼器(TMD)，本文采用TMD对该人行悬索桥进行振动控制。

5.1 TMD减振

TMD的减振系统主要由质量块、弹簧和阻尼3部分组成。关于TMD参数的计算，目前工程常用学者DEN[24]建立的经典TMD控制的最优参数计算公式，通过选取最佳阻尼比fopt和最佳频率比copt，可以使主系统和减振器谐振时，主系统的振动反应将会降到最小。DEN HARTOG提出的最优阻尼器参数λopt和ζopt，其计算公式为：

(3)

(4)

(5)

(6)

(7)

copt=2ζoptλoptω0md

(8)

其中，μ是阻尼装置质量与主结构质量之比；fopt是TMD的最优频率；ω0为主结构的角频率；md为TMD质量；ωd为TMD的角频率。

5.2 TMD减振研究

TMD质量比的取值范围一般为0%～5%，为了研究质量比对结构动力响应的影响，以0.2%的增幅拟定质量比的值，分别计算其对应的刚度和阻尼比，将计算所得的参数应用到该人行悬索桥中进行模拟，以之前设计的人群荷载工况施加节点动力荷载，分别得到最大的竖向加速度响应值。

根据计算结果，拟合了TMD质量比对结构竖向加速度响应峰值的曲线，如图17所示。从图中可以看出，加速度响应随着TMD质量比的增大而减小，但当质量比超过1.25%时，TMD的减振效率出现了明显的下降，虽然质量比的增加依然可以减小加速度响应峰值，但同时TMD的质量开始大幅度增加，经济性降低。

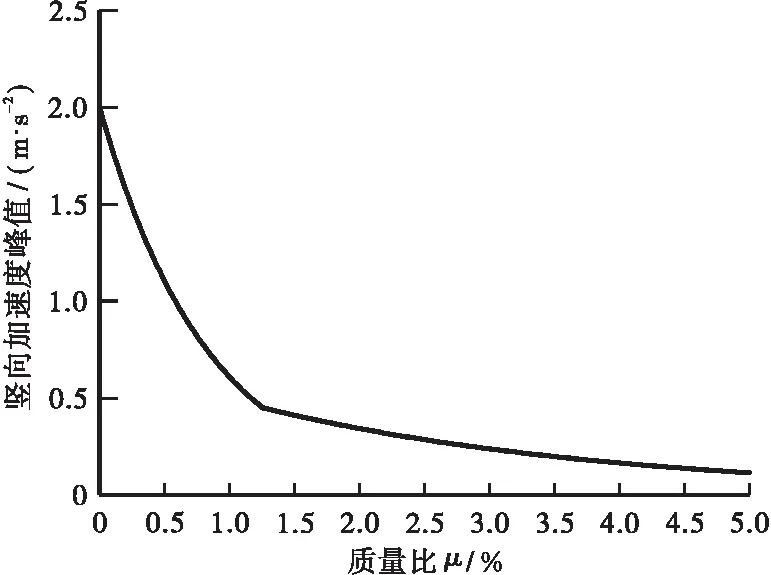
图17 质量比与竖向加速度峰值的影响

综合考虑质量比对TMD减振能力和效率的影响，结合该人行悬索桥对于人致振动舒适度的要求，选择1.25%作为TMD的质量比，计算得到其TMD的参数，如下：质量240.86 kg，频率1.998 Hz，刚度37 490.81 N/m，阻尼410.199 N/s。根据有限元分析，TMD启用后可使该人行悬索桥的竖向加速度峰值降低为0.452 m/s2，减振效率达到了77.4%，减振后结构的人致振动响应满足规范对舒适度的要求。TMD的减振效果如图18所示。

图18 跨中竖向加速度时程曲线对比

TMD的减振效果除了与TMD的参数有关之外，TMD的个数和安装位置也对结构振动响应有重要影响。为了研究TMD个数和安装位置对结构减振效果的影响，在前面计算结果的基础上，指定TND的总质量比为1.25%，采取多种方案研究这两个因素的影响。TMD方案效果对比如表8所示。

表8 TMD方案减振效果比较Table 8 Comparison of vibration reduction effect of TMD scheme方案编号安装方案竖向加速度峰值/(m·s-2)减振效率11个,位于跨中0.40180%22个,跨中位置0.54173%33个,跨中位置0.56172%43个,1/4跨、跨中和3/4跨位置0.94253%53个,两个1/3跨和跨中位置0.88256%

从表8可知，TMD安装在跨中位置时，减振效果最好，将其安装在其他位置时，减振效果出现较为明显的下降。对TMD的安装个数，安装数量越多，安装位置越分散，效果越差。当所有的TMD均安装在同一个位置时，TMD个数越多，减振效果越差，但是减小幅度很小。

6 结论

目前，全国范围内的人行悬索桥的建设正如火如荼地进行，人行悬索桥景观效果好，但结构十分轻柔，人致振动舒适度问题十分突出。本文以陕北某人行悬索桥为研究对象，对其进行了人致振动分析，并且在其建成之后开展了现场测试试验，测试了人行悬索桥的动力特性和人致振动响应，并将测试结果与有限元分析值进行了进行对比分析，综合评价了该桥的舒适度是否满足要求。在确定该桥的竖向加速度响应超过规范要求后，依据经典的TMD的参数优选方法，进行了TMD减振效果分析。主要结论如下：

a.对于该人行悬索桥而言，按规范指定的方法进行有限元分析得到的加速度响应值与实桥上测得的竖向加速度响应值均超过了规范的限值，这验证了人行悬索桥人致振动问题十分突出，考虑到人行悬索桥所处的环境，有必要采取措施进行振动控制。

b.根据现场实测结果显示，该桥的竖向振动基频与行人的正常行走步频范围重合度较高。在行人密度小于0.7 人/m2时，该桥的竖向加速度响应与人群密度呈正相关，行人频率与结构基频越接近，随人群密度的增长幅度就越大。

c.人群的行走方式对结构的振动响应有一定的影响，多列同向行走，使得人群更加集中，增加了同步的概率，使得结构的振动响应有所增大。

d.TMD的安装可以显著降低结构的振动响应，但TMD的减振能力与TMD的质量比、安装位置和个数相关。TMD的质量比越大，减振能力越强，但当TMD的质量比超过某一值之后，减振效率显著下降。