多因素耦合翻立领样板生成模型构建
2023-01-15郭子翊黄振华龙颖邹奉元
郭子翊,黄振华,龙颖,邹奉元*,2,3
(1.浙江理工大学 服装学院,浙江 杭州 310018;2.浙江理工大学 丝绸文化传承与产品设计数字化技术文化和旅游部重点实验室,浙江 杭州 310018;3.浙江理工大学 浙江省服装工程技术研究中心,浙江 杭州 310018)
随着信息技术的快速发展,服装业逐步走向数字化、自动化和智能化,服装样板自动生成是服装CAD技术的重要研究方向之一,在服装远程定制、服装智能制造等领域有着巨大的应用潜力[1]。
大量研究围绕样板自动生成展开。HAN H S等[2]为解决服装定制中样板需要逐个手动创建的问题,制定依据身体测量值的预测样板放码规则,并通过分级法调整样板。刘肖等[3]为消除款式图和样板图信息表达之间的误差,建立两者的参数化关系,实现领、袖部款式图到样板图的转化。GU B等[4]为满足消费者对个性化服装的需求,利用Imageware软件测量女性身体点云数据,运用SPSS软件制定高度计算规则,再通过回归分析建立人体数据预测模型,最后利用CAD系统实现女式西服参数化样板的自动生成。LIU K X等[5]运用三维扫描技术,对120名女性身体数据进行测量,将身高、臀围和腰围作为关键尺寸输入BP-ANN模型训练,预测人体下体其他尺寸并生成样板,运用虚拟试穿系统对样板进行验证与调整。刘为敏等[6]为快速得出适合顾客体型的样板,运用BP神经网络算法构建基于人体腰围、臀围尺寸的神经网络模型,实现样板的自动生成,减少服装制版对样板师的依赖。LEE W等[7]为解决参数化样板不合体的问题,提出二次参数化模型修正方法,提高了参数化样板的合体度。LIU K X等[8]提出了一种基于人体尺寸的服装样板参数化设计方法,以牛仔裤为例,通过牛仔裤廓型、长度和腰高以及人体身高、腰围和臀围得到牛仔裤样板,并运用三维虚拟试穿调整样板参数。LIU K X等[9]就款式图与样板图独立生成造成生产效率低的问题,利用款式图、人体与样板的关系构建数学模型,将款式图数据加入样板生成的规则中,实现款式图与样板图的转化。
相同样板在不同面料下制作的成衣会有不同造型[10-11]。张莎莎等[12]为研究面料性能对A字裙的影响,提取了A字裙多个方向图像面积、裙宽、裙厚、波浪个数等造型参数指标,最后用相关分析和回归分析得到了具有显著影响的面料性能指标。针对面料性能与翻领间隙量影响关系不明确的问题,吴志明等[10]研究了面料性能对连翻领间隙量的影响,以及当翻领宽与领座高的差值变化时,面料性能对翻领间隙量变化规律的影响。杨晓敏等[11]针对翻驳领倒伏量难以设计的问题,运用KES-FB织物风格测试仪测量面料力学性能,通过主成分分析得到拉伸回弹性、压缩回弹性和单位面积质量为显著影响因子,基于回归分析得出面料力学性能参数与翻驳领倒伏量的定量关系。但以上研究仅考虑了面料因素或款式图参数对样板的影响,均未将样板生成视为面料与款式图共同作用的结果。
综上,目前样板生成的研究均未从面料和款式图的耦合作用展开,影响了样板生成中尺寸的预测精度。因此,文中采用Lasso回归算法,将面料性能和款式图参数耦合到PSO-RBF神经网络中,以翻立领为例,确定款式图与面料中的影响因子,构建面料参数与款式图参数多因素耦合的样板生成模型。
1 实验部分
文中数据源于浙江某制衣公司,通过分析生产工艺单,筛选出69张翻领款式图及每张款式图对应的样板图。翻立领款式图及其对应的样板图示例如图1所示。
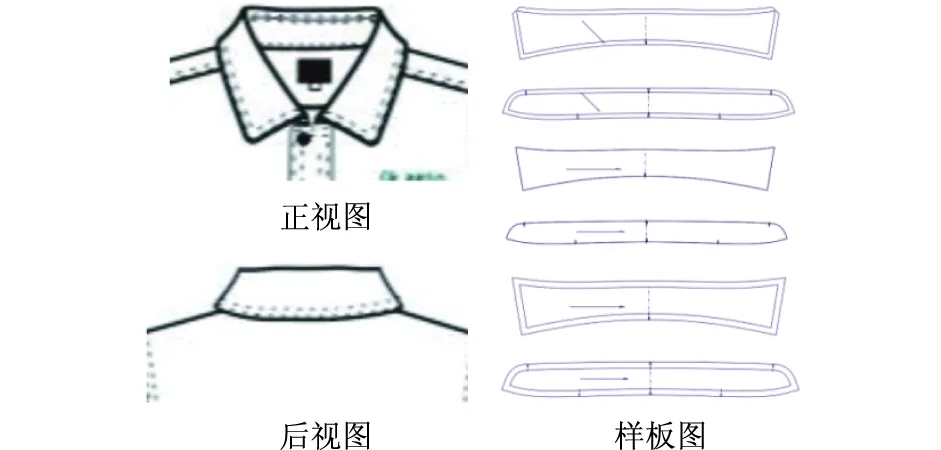
图1 翻立领款式图及其对应的样板图Fig.1 Lapel collar style chart corresponding to the sample chart
1.1 领型数据获取
1.1.1样板数据获取 翻立领生成过程中使用底领下口线、起翘量、底领上口线、底领高、间隙量,翻领高、翻领宽、翻领下口线和翻领外口线等9个样板参数,如图2所示。在实际翻立领样板生成过程中,只需要得到翻领下口线、起翘量、底领高、间隙量、翻领高和翻领宽6个变量,就可确定领子整体造型[13]。因此,文中实验在对样板图测量时仅对这6个变量进行测量。

图2 翻立领样板Fig.2 Pattern of the collar flat
1.1.2款式图数据获取 运用dizimizer软件对浙江某制衣企业提供的生产工艺单中的服装款式图进行测量。该软件将两点之间像素作为测量数值,并将其保存为Excel文件,作为预测模型的样本库。由于每张款式图的格式大小不同,导致在统一标尺下测量数据误差较大。因此记录工艺单中的衣长,并测量款式图中的衣长,对款式图进行修正。款式图比例标尺如图3所示。
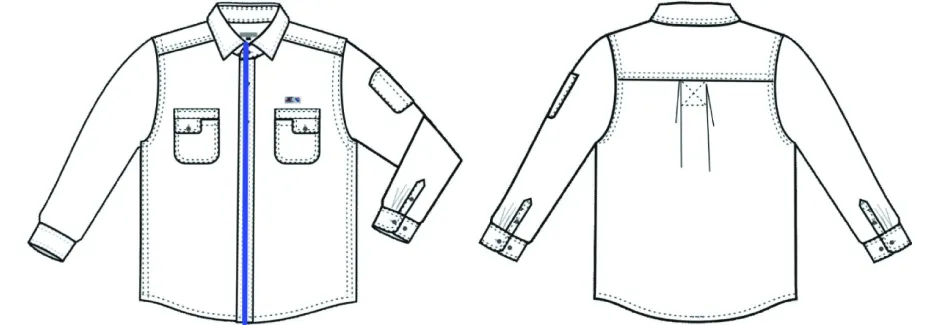
图3 款式图比例标尺Fig.3 Style drawing scale
款式图和样板图测量值对比如图4所示。文中将数据分为固定值、预测值和设计值。首先,在获取样板领型变量时,采用领围为40 cm的样板进行测量,把领子样板生成过程中底领下口线定为常量,减少需要预测的变量;其次,样板翻领高、翻领宽和底领高在款式图上都有对应的部位,因此视其为预测值,将款式图与样板图的差作为输出值;最后,将间隙量和起翘量作为设计值。
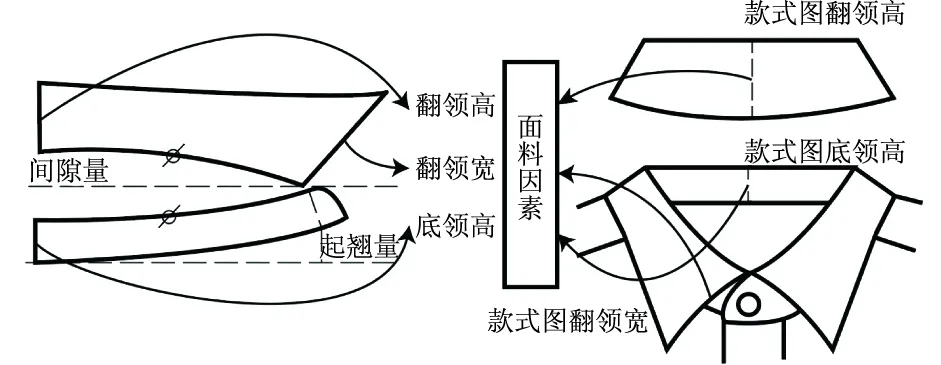
图4 款式图和样板图测量值对比Fig.4 Comparison of measurements between style and sample drawings
1.2 面料性能测定
1.2.1仪器 XY精密电子天平,常州幸运电子设备有限公司制造;YG(B)141D数字式织物厚度仪,YG026PC-250电子强力机,YG(B)022D自动织物硬挺度试验仪,均由温州际高检测仪器有限公司制造;YG541E全自动织物折皱弹性仪,宁波纺织仪器厂制造;YG800织物悬垂性测定仪,闽测仪器设备(厦门)有限公司制造;Escan三维扫描仪,先临三维科技股份有限公司制造。
1.2.2面料 文中所选面料为浙江蓝天制衣有限公司的工装制服面料,面料成分主要为棉和涤纶,面料的基本规格参数见表1。
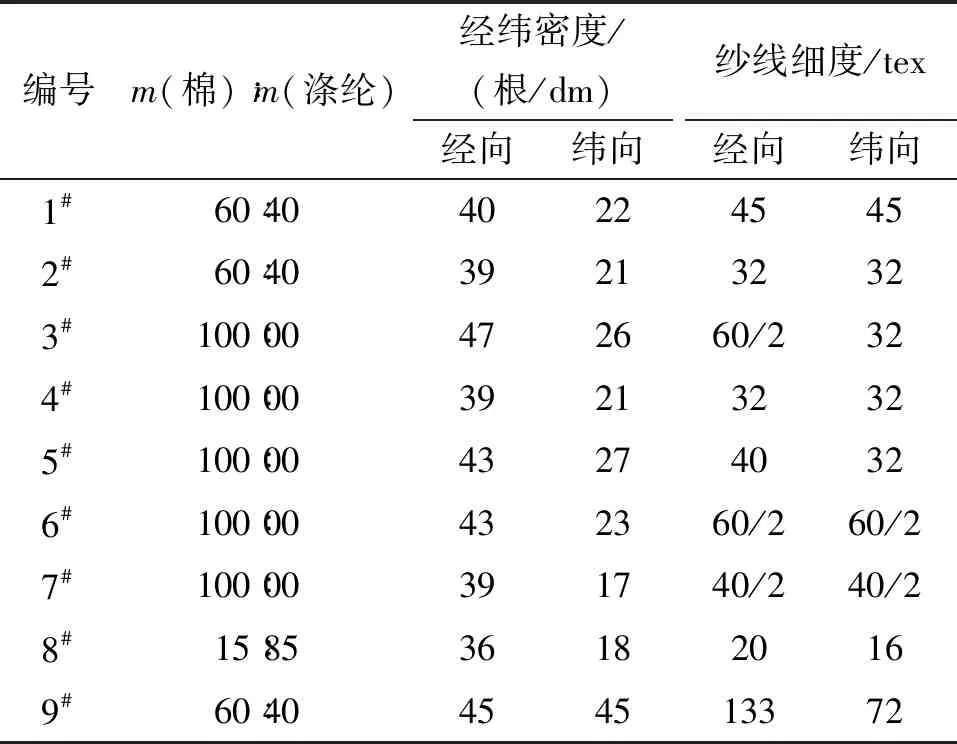
表1 面料基本规格参数Tab.1 Basic fabric specifications
1.2.3方法 实验要测定的面料性能指标有面密度、厚度、拉伸性能、弯曲性能、压缩特性和悬垂性[10-11],严格按照面料性能测试要求,每个项目均测量3次取平均值。
1.2.4结果 9种面料的性能测试结果见表2。
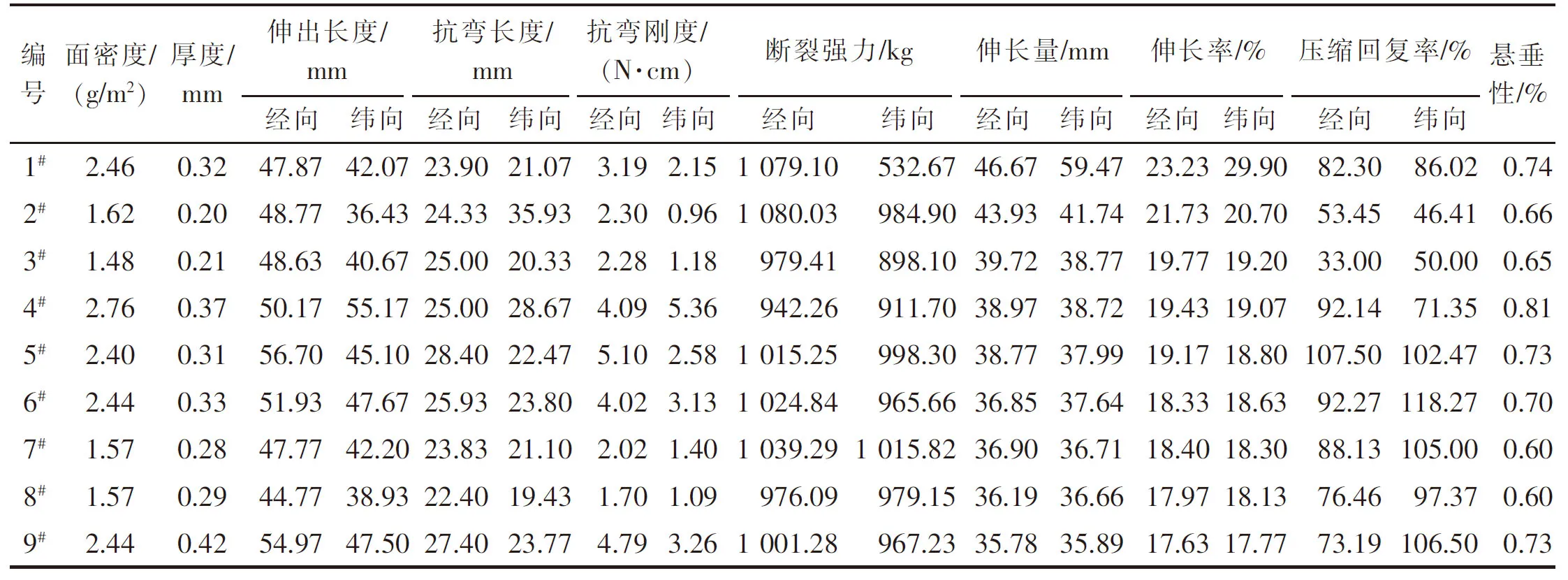
表2 面料性能指标Tab.2 Fabric mechanical properties
1.3 输入数据优化
针对不同领型样板数据采用不同的输入方式。首先针对预测值,以面料参数作为输入,以款式图与样板图差值作为输出,对测量数据进行偏移校准。而对于设计值,则选用款式图底领高、翻领高、翻领宽以及面料参数作为输入,间隙量和起翘量作为输出。
由于设计值输入数据为款式图数据和面料数据,输入数据过多且为离散数据,因此选择Lasso回归算法实现变量的筛选,在变量筛选同时对复杂度进行调整。构建Lasso模型主要分为3步。
1)读取款式图、面料和样板数据,构建Lasso模型的输入与输出,将数据集的80%作为训练集,20%的数据作为测试集。
2)定义Lasso回归算法分析函数,对数据集进行回归分析,并输出回归效果和对应变量的回归系数,通过此方法确定惩罚范数L1的取值。L1正则化公式如下:

式中,X,y为训练样本和相应标签;w为权重系数向量;f为目标函数;Ω即为惩罚项;参数α控制正则化强弱。
3)采用步骤2)所得的Alpha参数对款式图和面料参数进行降维。
1.4 Lasso参数降维
面料数据与款式图数据共有26个变量,将26个变量输入PSO-RBF神经网络会形成噪声,从而干扰网络的性能,因此运用Lasso回归算法对数据进行降维。Lasso回归算法分析结果见表3。在Alpha=1时,训练得分与运用的特征数均为0,表明在该惩罚值下将所有变量特征均剔除了。随着Alpha值的下降,训练得分和测试得分在逐渐上升,当Alpha<0.01时,训练得分继续上升,而测试得分不断下降并出现负值,说明网络出现过拟合现象。因此本实验确定Alpha的值为0.01。
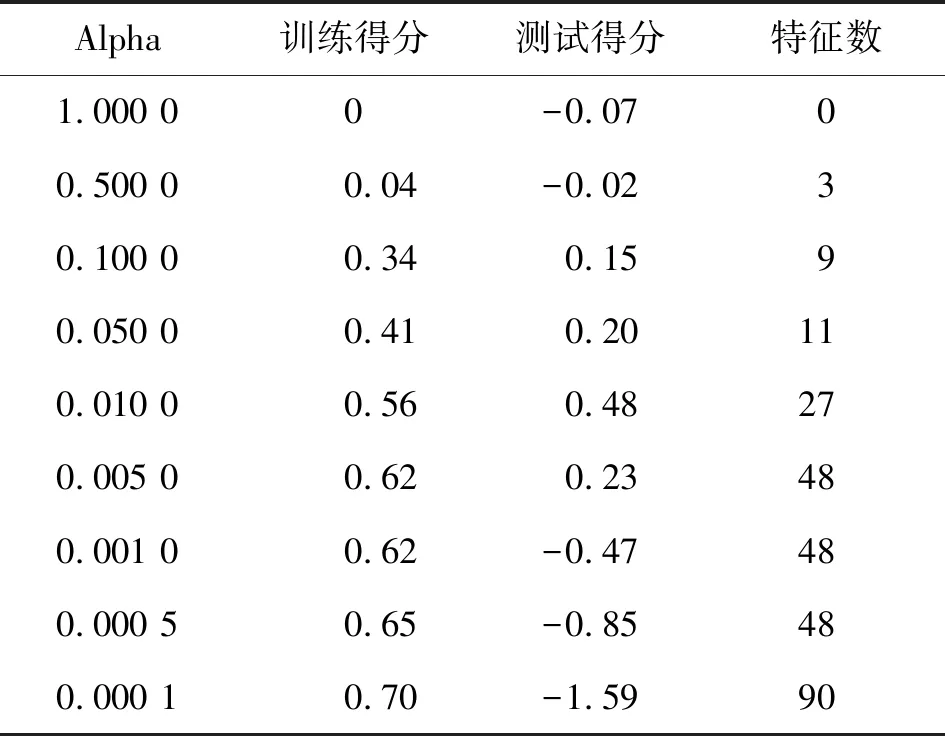
表3 Lasso回归算法分析结果Tab.3 Results of Lasso regression algorithm analysis
将款式图数据和面料数据输入构建好的Lasso模型进行参数化降维,Lasso模型其他参数见表4。数据输入时将数据进行归一化(normalize)并加入常数项(fit_intercept)有利于模型回归。

表4 Lasso模型参数Tab.4 Parameters of lasso model
预测量结果见表5,可见厚度影响最大,因此预测量仅考虑厚度的影响。各差值与厚度的关系如图5所示。
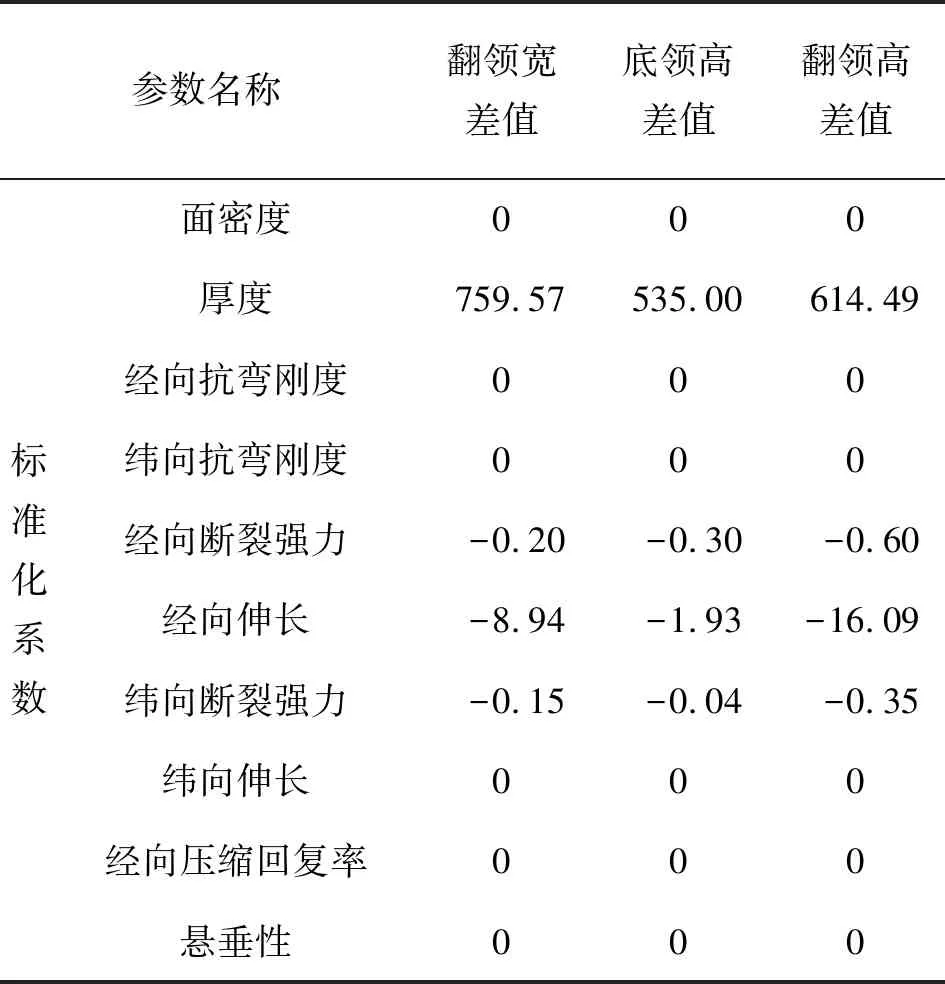
表5 预测量Lasso模型结果Tab.5 Results of Lasso regression algorithm analysis

图5 预测量预测结果Fig.5 Predicted volume forecast results
设计量Lasso降维结果见表6。在23个变量中,影响起翘量回归的面料因素为面料厚度、经向抗弯刚度、纬向抗弯刚度、经向断裂强力、经向压缩回复率;影响间隙量的仅有厚度和纬向抗弯刚度。
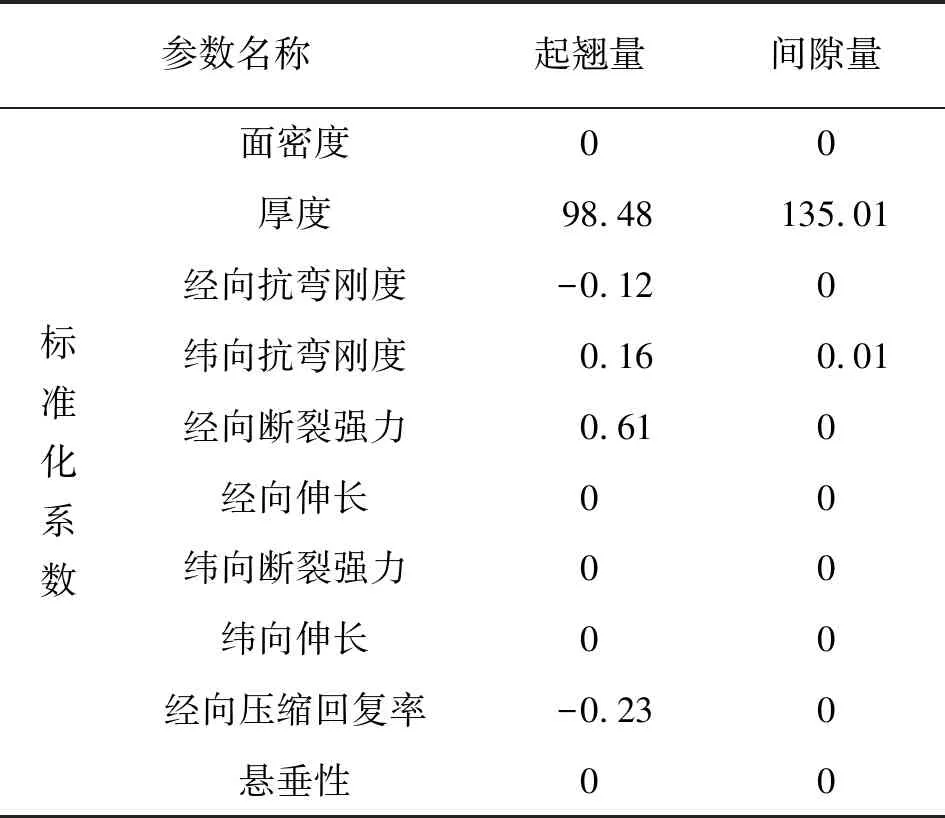
表6 设计量Lasso模型结果Tab.6 Results of Lasso regression algorithm analysis
1.5 翻立领预测模型的构建
为提高模型精度,针对设计量构建了PSO-RBF网络模型[14],其分为两个部分:径向基神经网络 (RBF) 和粒子群算法 (PSO)。其中,RBF是一种具有单隐层的3层前馈型神经网络,其包括输入层、隐含层、输出层。RBF激活函数为
式中,X-XP为欧式范数;XP为高斯函数的中心;δ为方差。
RBF神经网络的输出为
式中,Yj是第j个输出单元的输出值,j=1,2,…,n;Wij是第i个隐含层节点到第j个输出层节点的连接权值。
粒子群算法流程主要分为3步。①对粒子群基本参数进行设定。确定粒子群算法的迭代次数,根据实验任务设置粒子群规模,确定函数的自变量个数与粒子的最大速度与位置信息,及随机初始化速度和位置。②定义适应度函数,与历史全局最优解比较进行迭代更新。③迭代次数达到设定值或全局最优解差值满足设定的界限后停止。其中,更新速度和位置为

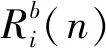
1.6 评价指标
为了分析预测效果,文中采用平均绝对误差作为评价指标对预测效果进行评估。平均绝对误差综合评价了网络的预测性能,得到的值越小,证明预测的精度越好。其中平均绝对误差(E)为
2 实验结果
2.1 网络训练结果
将优化后的数据放入PSO-RBF网络,每个预测参数的均方误差结果如图6所示。

图6 优化PSO-RBF网络训练结果Fig.6 Optimization of PSO-RBF network training results
2.2 对比实验结果
使用常用的BP神经网络和PSO-PBF网络作为对照组,4个样板参数绝对误差如图7所示。由图7可知引入面料参数后的网络更加稳定,且误差普遍较低。
加入面料参数的PSO-RBF和未加入面料参数的PSO-RBF的间隙量和起翘量对比实验如图7所示。其中,加入面料参数的PSO-RBF起翘量平均绝对误差为0.37 cm,而未加入面料参数的PSO-RBF的起翘量平均绝对误差为0.58 cm。加入面料参数的PSO-RBF间隙量平均绝对误差为0.15 cm,而未加入面料参数的PSO-RBF的间隙量值平均绝对误差为0.61 cm。
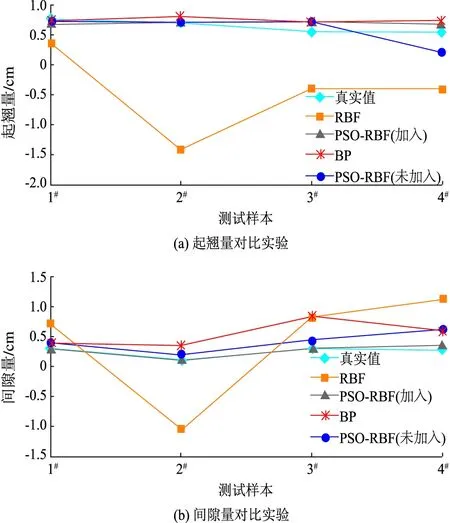
图7 对比实验结果Fig.7 Comparison of the experimental results
由实验可得,面料性能对样板自动生成的影响因子主要有厚度、悬垂性;款式图参数对领子样板自动生成的影响因子主要有底领高、翻领高、翻领宽。融入面料参数的PSO-PBF起翘量平均绝对误差较BP神经网络降低了0.23 cm,较未融入面料参数的PSO-PBF降低了0.21 cm。融入面料参数的PSO-PBF间隙量平均绝对误差较BP神经网络降低了0.41 cm,较未融入面料参数的PSO-PBF降低了0.46 cm。
2.3 实物制作与比较
文中选取了最后一个样本的未加入面料因素与加入面料因素的PSO-RBF模型实物进行比较。为增加对比的可信度,选用Escan三维扫描仪分别扫描未加入面料因素与加入面料因素的PSO-RBF模型的实物以及标准样本实物,具体如图8所示。在Geomagic design X软件中将两个模型进行了对齐,结果显示,加入面料因素的领子与原样版的领子更为贴近。

图8 实物验证Fig.8 Physical patterns verification
3 结语
文中引入Lasso回归算法,将面料性能耦合到PSO-RBF神经网络中,确定款式图与面料参数中的影响因子,构建了面料参数与款式图参数共同耦合的样板生成模型。经对比实验,验证了加入面料性能参数能够减少样板数据的预测误差。主要结论如下:
1)未加入面料参数的PSO-RBF的间隙量平均绝对误差为0.61 cm,而加入面料参数的PSO-RBF间隙量平均绝对误差为0.15 cm,降低了0.46 cm。未加入面料参数的PSO-RBF的起翘量0.58 cm,加入面料参数的PSO-RBF起翘量平均绝对误差为0.37 cm,降低了0.21 cm
2)影响起翘量回归的面料因素为面料厚度、经向抗弯刚度、纬向抗弯刚度、经向断裂强力、经向折皱;影响间隙量的面料因素仅有厚度和纬向抗弯刚度。面料厚度和抗弯刚度对领子起翘量起正向作用,厚度较厚时,需要更多的起翘量和间隙量来满足领子下弯的曲度;刚度越高,领子身骨越刚硬,同样需要更多的起翘量和间隙量。
3)面料厚度影响款式图与样板图的底领高,面料厚度越厚,翻领高与翻领宽两者差值越大,这与常识相同。
同时,文中只针对款式图参数和面料参数实现样板自动生成,今后将聚焦于自动提取款式图参数,实现样板生成的完整性。
