基于数据分析的污水监测采样点数据研究

周希杰，田博文，郑宏飞，张 昱

（1.阜阳师范大学，安徽 阜阳 236041；2.徽商银行股份有限公司亳州分行，安徽 亳州 236800；3.安徽职业技术学院，安徽 合肥 230011）

1 数据预处理

模型的成功率取决于数据质量和数量，由于受到可靠性和人为因素的影响，采样人员采集的数据会存在异常等情况，如果直接用这些数据来预测会导致模型的成功率下降，而且输入变量众多且相互影响，所以必须对样本数据进行预处理，对原始数据做异常值剔除、归一化和缺失值处理等［1］。

1.1 异常值处理

如果直接波动较大的数据进行预测，将会导致预测成功率的下降，甚至预测结果完全偏离实际值，所以要剔除异常值，剔除方法采用的是拉依达准则，即3σ准则：当偏差大于3σ的时候，该数据为异常值，需要被及时剔除，σ的计算公式为：

当偏差大于3σ时，该数据为异常值，异常值的判断准则如下：

因此，正常数据的范围为xi＞3σ+x和xi＜x-3σ，剔除完剩下的即为正常值。

1.2 缺失值处理

为了满足数据的完整性，技术人员需填补缺失数据。常用的缺失值填充方法有随机填补、均值法、中位数法、众数法等数据填充，也有K-最近邻法、回归预测法、期望值最大法等建模数据填充方法。我们对数据进行了初步统计，部分特征变量的数据存在较多缺失值，数据缺失和在上述异常数据处理时剔除掉一些数据。数据缺失值的处理如下：ptc_15d：具有30 000个以上的缺失值，对缺失值样本数据进行剔除；detect_prop_15d：具有18 000个以上的缺失值，对缺失值样本数据进行剔除。

1.3 归一化处理

数据存在不同的量纲单位，因此数据大小差别非常大，数据范围也不相同。差异较大会增大某些变量对预测结果的影响，同时会减弱某些变量对预报模型的影响，所以需要对剔除异常值后的数据进行归一化。将所有数据都转化为［0,1］之间的数，可以消除因数据大小不一而造成的偏差，最后对模型计算结果进行反归一化还原。数据的归一化有很多方法，本文采用最大最小法进行归一化处理，对数据进行归一化处理的公式如下：

2 模型的建立

2.1 基于强化学习的特征选择模型（RLFS）

强化学习是机器学习中的一个领域，其基本思想是从环境中得到反馈而学习，即所谓的试错学习方法。在学习过程中，智能体Agent不断地尝试进行选择，并根据环境的反馈调整动作的评价值。研究发现传统特征选择算法存在着不足，或是选择的特征子集在进行分类任务时准确率较低，或是选择的特征子集规模较大。因此本文结合强化学习的决策能力和Wrapper特征选择方法，提出了一种基于强化学习的特征选择方法（Reinforcement Learning for Feature Selection,RLFS），将强化学习的学习和决策能力应用于特征选择过程中，通过训练学习得到特征子集，最后通过仿真实验证明了RLFS方法具有良好的降维能力，并有较高的预测准确率，实现思路见图1。

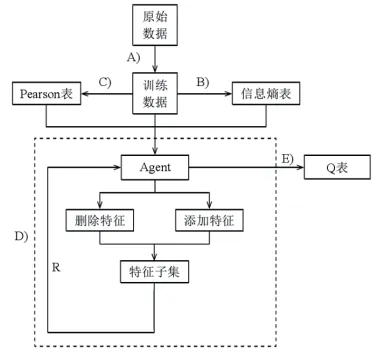
图1 RLFS算法示意图

步骤A到E所代表的处理过程如下：A）数据预处理，包括对原始数据集进行归一化和离散化处理，得到训练数据。B）计算每个特征的信息嫡和信息嫡均值，并将特征信息嫡高于信息嫡均值的特征记录在信息嫡表中。C）计算每两个特征Pearson相关系数以及Pearson相关系数的均值，将高于Pearson相关系数均值的特征对记录在Pearson 表中。Pearson相关系数反映了两个变量间的线性相关程度，是一种线性相关系数。假设，X,Y为随机变量，两个随机变量的Pearson相关系数定义如下:

其中，，分别为X，Y的均值，px，y的取值在［-1,1］之间，该值反映了两个变量线性相关性的强弱程度，其绝对值越大说明相关性越强。当其取值-1或1时，表示两个变量完全相关，取值为0时，表明两个变量不是线性相关，但可能存在其他方式的相关性。当两个特征的Pearson相关系数绝对值较大时，两特征中有冗余特征的可能性也较大。在特征选择过程中计算特征间的Pearson相关系数，剔除特征空间中相关系数较大的一对特征中的一个特征，尽量减少冗余特征。D）此步骤为Q学习算法中Agent进行迭代训练学习并逐步进行决策的核心过程。将训练数据和Pearson表以及信息嫡表代入Agent,Agent根据添加和删除特征的动作所带来的不同收益作出决策。E）当Agent训练学习完成后输出Q表，通过对Q表的分析得到经过RLFS算法选择后的特征子集。经过Python编程计算可以得出指标的评分如图2所示。

图2 重要特征得分

由图2可得出，影响国内污水监测采样点分布（得分大于1 000）的特征wwtp_id和population_served 2个特征，其中wwtp_id和population_served得分较高，是最重要的特征，其对各地区采样点总数影响较大。由于wwtp_id和各地区采样点总数基本类似，我们使用population_served进行分析。

2.2 污水监测采样点综合评价模型

为增加10个污水监测采样点，需要选择最合理的位置设置污水监测采样点，并通过对已有采样点进行评价，构建污水监测采样点综合评价模型，评分越高，说明该地区污水监测采样点对污水的监控不足，更需要增加，评价公式为：

其中Q代表缺陷程度得分，Sum代表wwtp_id计数值，Average代表population_served平均值。

3 模型的求解

3.1 正态性检验

通过绘制平均的population_served数据的QQ图，鉴别样本数据是否接近于正态分布。

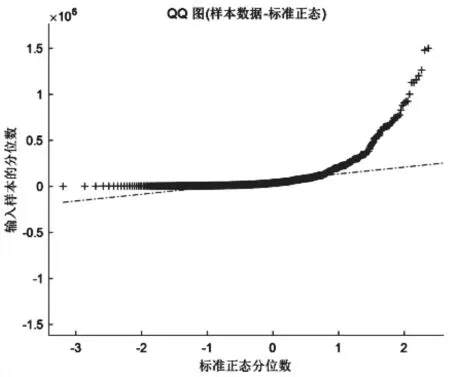
图3 Q-Q图

观察Q-Q图发现大部分样本点近似地分布在一条直线附近，因此可以判断样本数据近似于正态分布。

3.2 Pearson相关系数计算

wwtp_id升序排列，部分计算数据见表1。

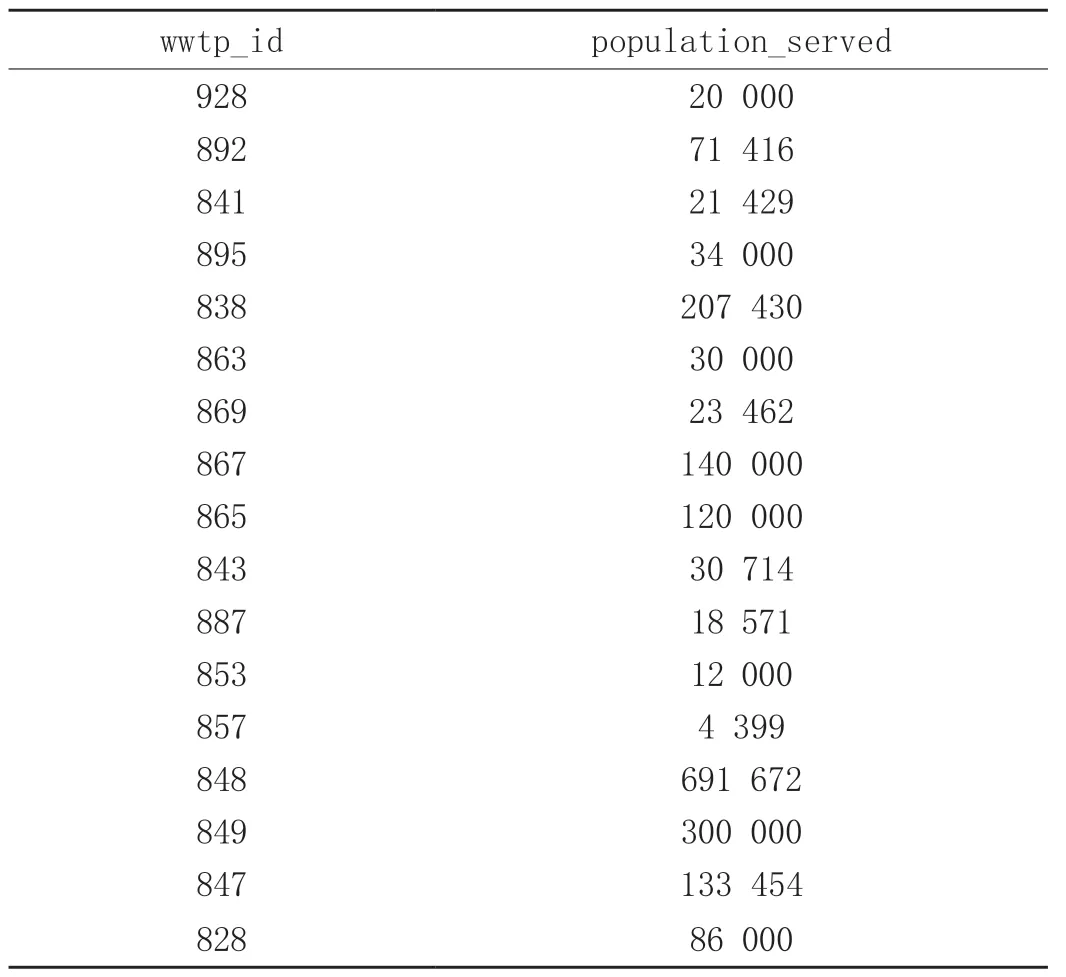
表1 Pearson相关系数数据

我们通过Matlab进行编程，得出wwtp_id与population_served 的相关系数为0.742，说明污水监测采样点分布的合理性不高。

3.3 污水监测采样点综合评价模型

通过计算得出污水监测采样点综合评价得分，wwtp_id升序排列，部分数据见表2。

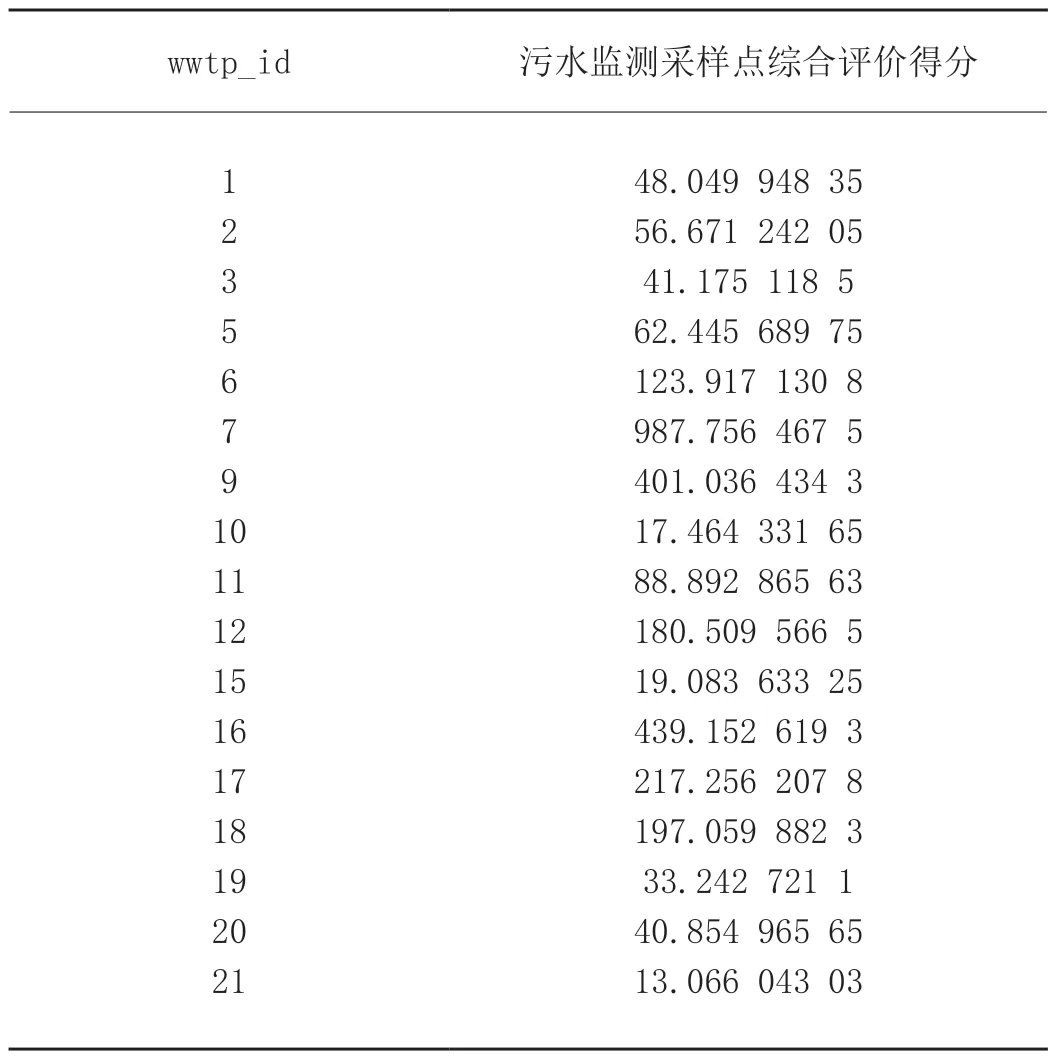
表2 缺陷评价得分

然后对评价得分进行降序排列，结果如图4所示。

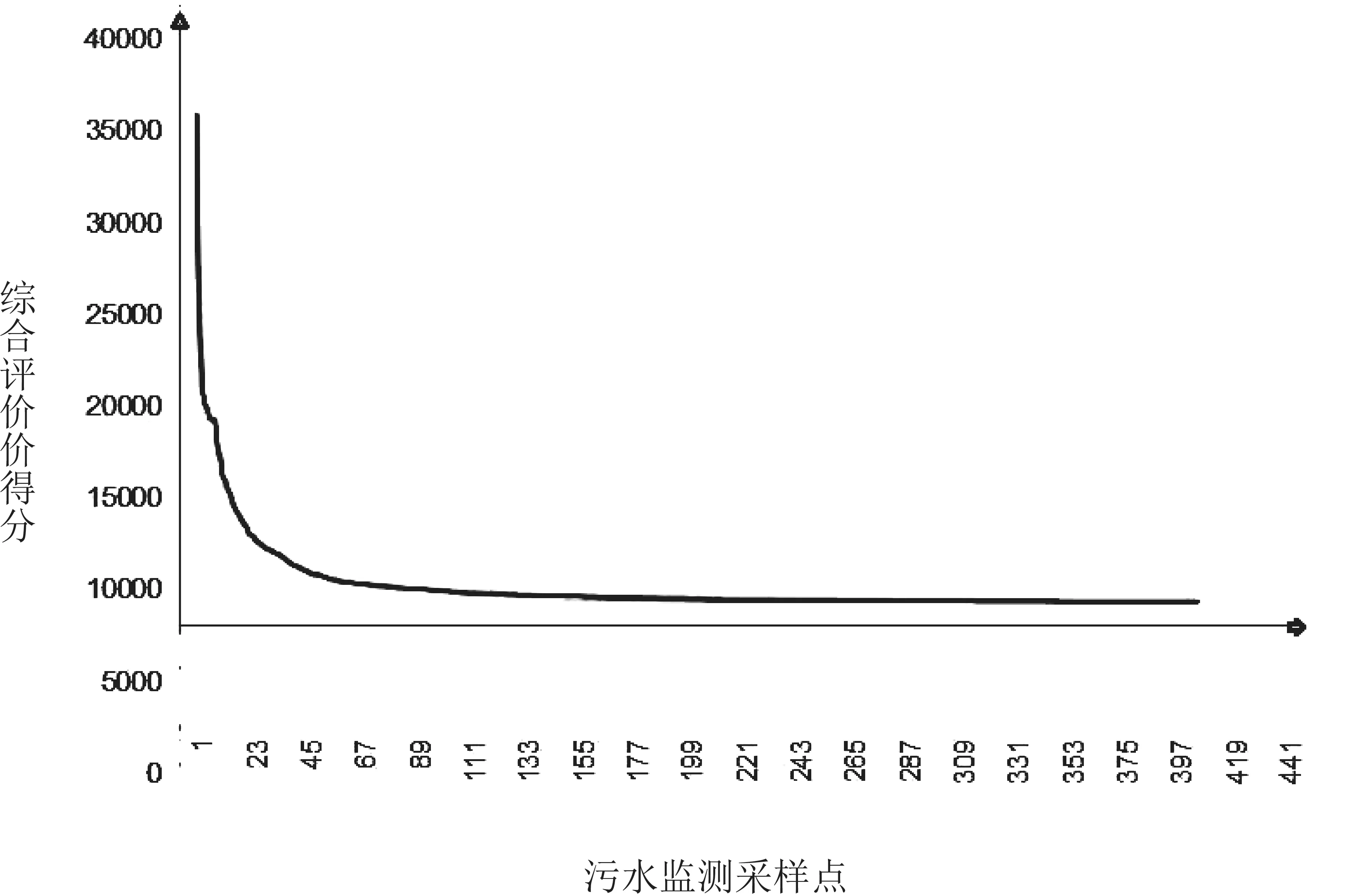
图4 污水监测采样点综合评价得分（得分降序排列）

挑选得分排名前十的作为污水监测需要增加的十个采样点，详见表3。

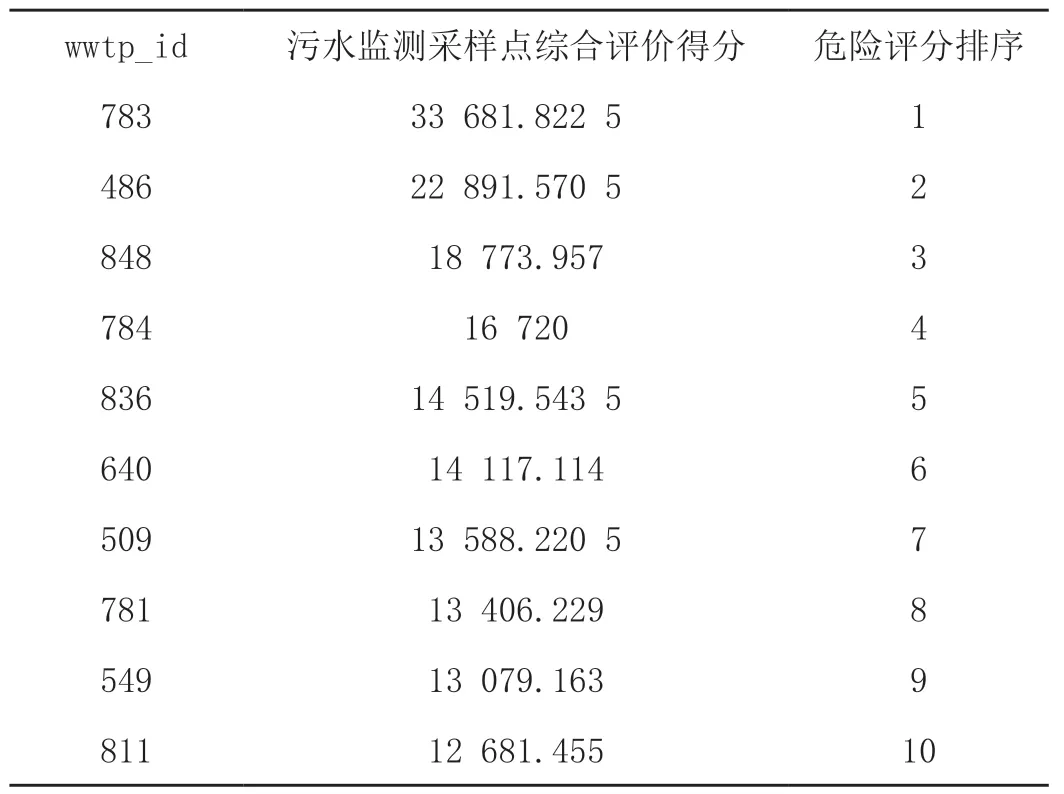
表3 增加的十个采样点

4 结果结论

（1）首先对数据进行缺陷值、异常值以及归一化等数据预处理，其次通过基于强化学习的特征选择模型（RLFS），对特征进行筛选，最后通过计算特征与污水监测采样点的Pearson相关系数，得出wwtp_id与population_served的相关系数为 0.742，说明污水监测采样点的分布合理性不高。

（2）通过污水监测采样点综合评价对污水监测采样点进行评价，筛选出wwtp_id分别为 783、486、848、784、836、640、509、781、549和811的重要区域增加10个采样点。