序超半群的相对超理想

谢祥云, 李春燕, 赵云平

(五邑大学 数学与计算科学学院,广东 江门 529020)

1 引言与预备知识

若一个代数系统(S,·)满足结合律,即(xy)z=x(yz),∀x,y,z∈S[1],则称(S,·)为半群.若(S,·)是一个半群,(S,≤)是偏序集且对于任意给定的a,b,c∈S,有a≤b⟹ac≤bc,ca≤cb,∀c∈S，则称(S,·,≤)为一个序半群[2].

序半群理论在理论计算机科学、码论、形式语言等领域有广泛的应用,理想论是研究半群代数结构的一个非常理想的途径,大量的文献涉及理想论的思想[1, 3-6].1962年,Wallace在半群上首次引入相对理想(H-理想)的概念,并在1963年继续发文研究相对理想的拓扑性质[7-8].1967年,Hrmova进一步研究了相对理想的性质,并根据相对理想引入了Green关系[9],2020年Khan等将相对理想的概念进一步推广到序半群上,研究了序半群上理想、素理想、双理想和拟理想的性质并对半群进行了刻画[10-11].

1934年,法国数学家F.Marty提出了超结构[12]的概念,作为经典代数结构的泛化, 在超结构中两个元素的运算是一个集合.真正地将半群代数理论与超结构完美结合的是印度数学家M.K.Sen,他研究了模糊超半群的相关理论[13].从1999年以来,伊朗数学家B.Davvaz等在建立超半群的基本理论方面做了一些基础工作,如超半群上的正则二元关系、超半群的超理想[14]、超半群上的同余[15-22]等.

在此基础上,本文将半群上的相对理想概念推广到了序超理想, 给出了相对超理想的基本性质.作为特例,文献[10-11]的相关结论是本文的推论, 在论证过程中指出了文献[10-11]中的相关错误.

定义1[14]称映射∘:S×S→P*(S)为S上的一个超运算,其中S是非空集,P*(S)是S的非空幂集, 称(S,∘)为一个超群胚.

令(S,≤)为一个偏序集,若a≤b蕴含a∘c≤b∘c且c∘a≤c∘b,∀c∈S，则称(S,∘,≤)[19]是一个序超半群.当A,B是S的非空子集时,我们定义A≤B当且仅当(∀a∈A)(∃b∈B)a≤b.为了方便，以下也常称为序超半群S.

若序超半群S的一个非空子集I满足

(ⅰ)S∘I⊆I,I∘S⊆I，

(ⅱ)若a∈I,b≤a,b∈S,则b∈I，

则称I为超理想;类似地,我们可以引入序超半群的超左理想、超右理想等.

本文用到的基本概念和术语如果没有说明可参考文献[1,12].

2 相对超理想

定义3设S为一个序超半群,A,T为S的任意非空子集.若由A∘T⊆A和Tx≤y∈A可得x∈A，则称A为S的右T-超理想.类似可定义S的左T-超理想.若A既是S的左T-超理想, 又是S的右T-超理想，则称A为S的T-超理想.若T=S, 则S的左T-超理想(右T-超理想,T-超理想)与S的左超理想(右超理想、超理想)一致.

注1序超半群S的一个超理想A对S的任意非空子集T是一个T-超理想, 反之不然.

例1设S=Z,对任意m,n∈Z, 定义S上的超运算m∘n={n,m}，则(S,∘,≤)是S上关于一般序关系的序超半群.令T={2},A=2Z,则T∘A=2Z⊆A，但S∘A=S≠A.

例2设S=Z,则(S,·)在S上关于一般意义上的乘法构成一个半群.对任意m,n∈Z, 定义m∘n={x∈Z|x≤mn}，则(S,∘,≤)是一个序超半群, 其中“≤”是S上的一般序关系.设A=2Z, 则

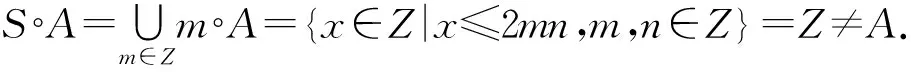
因此,A不是S的超理想.令T={2}, 则

T∘A=A∘T={x∈Z|x≤4n,n∈Z}=Z，

从而A不是S的T-超理想.令A={1,2,3,4,5,6},则A不是S的超理想.若T={1}, 则T∘A=A∘T=A.因此,A是S的T-超理想.

定义4令A和T为序超半群S的任意非空子集, 称集合

(A]T∶={t∈T|t≤a,a∈A}

为A相对于T的下凸集.

引理1令S为序超半群, 则下列命题成立：

(ⅰ)对所有的A⊆T,有A⊆(A]T；(ⅱ)若A⊆B⊆T,则(A]T⊆(B]T；(ⅲ)若T为S的子超半群,则(A]T(B]T⊆

(AB]T；(ⅳ)对每一个T-理想A⊆T, 有(A]T=A；(ⅴ)((A]T]T=(A]T；(ⅵ)若T,A是S的非空子集,则A∩T⊆(A]T.

证明引理1中大部分命题容易验证,我们仅证明(ⅲ)和(ⅴ).

(ⅲ) 设t∈(A]T(B]T, 存在a∈(A]T,b∈(B]T, 使得a≤x,b≤y,x∈A,y∈B，t∈a∘b≤x∘y⊆AB.因为T为子超半群, 所以a∘b⊆T, 从而t∈(AB]T.

(ⅴ)若x∈((A]T]T,则存在t∈(A]T使得x≤t.因为t∈(A]T,存在a∈A使得t≤a,所以x≤a,从而x∈(A]T.

反之,若x∈(A]T,则对于一些a∈A,存在x∈T,使得x≤a.因为x≤x∈(A]T,x∈T,所以x∈((A]T]T,从而(A]T⊆((A]T]T.设x∈((A]T]T,则存在y∈(A]T使得x≤y, 所以x∈(A]T. 反之显然.

性质1(ⅰ) 设(S,∘,≤)是序超半群,T是S的子超半群.若A,B是S关于T的超理想,则(AB]T,A∩B均为S中的T-超理想.

(ⅱ) 设(S,∘,≤)是一个序超半群,若T是S的子超半群,则对任意a∈S,(T∘a∘T]T是S中关于T的超理想.

证明(ⅰ) 若A,B是S中关于T的超理想,对于任意t∈T,x∈(A∘B]T,存在a∈A,b∈B使得x≤a∘b,则

t∘x≤t∘(a∘b)=(t∘a)∘b⊆A∘B.

因为T是S的子超半群,所以t∘x⊆T,从而t∘x⊆(A∘B]T.易知,若a≤b∈(A∘B]T,a∈T,则a∈(A∘B]T.类似于上面的证法,我们可以证明x∘t⊆T.因此(AB]T是S中关于T的超理想.

由T∘(A∩B)=T∘A∩T∘B⊆A∩B,(A∩B)∘T=A∘T∩B∘T⊆A∩B以及a≤b∈A∩B,a∈T可知a∈A∩B,从而A∩B均为S中关于T的超理想.

(ⅱ)若T是S的子超半群,对于任意t∈T,x∈(T∘a∘T]T,存在t1,t2∈T使得x≤t1∘a∘t2,则t∘x≤(t∘t1)∘a∘t2⊆T∘a∘T.因为T是S的子超半群,所以t∘x⊆T,t∘x⊆(T∘a∘T]T.类似地,可以证明x∘t⊆(T∘a∘T]T.若c∈T,c≤b∈(T∘a∘T]T,则c∈(T∘a∘T]T.

注2由于序半群是序超半群的特例,在性质1的证明中我们同时改正了文献[10]引理2.3中的一些错误.

下面我们进一步推广相对超理想.

定义5令S为一个序超半群,A1,A2是S的任意非空子集.若S的一个非空子集A满足A1∘A⊆A,A∘A2⊆A且对y∈A,A1∪A2x≤y, 有x∈A，则称A为S的一个(A1,A2)-超理想或(A1,A2)-相对超理想.若A1=∅或A2=∅, 则S的(A1,A2)-超理想为单边相对超理想.

我们将S的所有(A1,A2)-超理想表示为I(A1,A2).由S的(A1,A2)-超理想的定义易知(A1,A2)-超理想是左T-超理想、右T-超理想和双边T-超理想的推广.

例3设集合S={a,b,c,d},带有超运算“∘”(表1)和序“≤”关系：

表1 S上的超运算(例3)

≤∶={(a,a),(b,b),(c,c),(d,d),(a,d),(a,c),(d,c),(a,b),(d,b)}.

(1)

我们给出S的哈斯图(图1).

图1 序关系(1)的哈斯图(例3)

容易验证(S,∘,≤)是一个有序超半群.令A1={a},A2={d},A={a,d}, 则A1∘A⊆A;A∘A2⊆A.对y∈A,A1∪A2x≤y,有x∈A.从而A是S的一个(A1,A2)-超理想.S∘A={a,d}且∀x∈S, 若对y∈A, 有x≤y, 则x∈A.因此A是S的左超理想.由于S是交换的,同理,A是S的右超理想.

若在例3中令序关系如下：

≤1∶={(a,a),(b,b),(c,c),(d,d),(d,b),(d,a)},

(2)

图2 偏序关系(2)的哈斯图

下列性质容易证得.

性质2设S是一个序超半群, 则下列命题成立:

(ⅰ)若A1⊂A′1,A2⊂A′2,则I(A′1,A′2)⊆

I(A1,A2);

(ⅱ)I(A1,A2)=I(A1,∅)∩I(∅,A2).

定理1设S是一个序超半群,H1,H2是S的序子超半群，则下列命题成立:

(ⅰ)(H1∘a]H1∈I(H1,∅),a∈S;

(ⅱ)(a∘H2]H2∈I(∅,H2),a∈S;

(ⅲ)(H1∘a∘H2]H∈I(H1,H2),a∈S,H=H1∪H2⊇H1∘H2;

(ⅳ)若L∈L(H1,∅),R∈I(∅,H2),则

(L∘R]H∈I(H1,H2),H=H1∪H2⊇H1∘H2;

(ⅴ)若A,B∈I(H1,H2)使得A∩B≠∅, 则

(A∘B]H,A∩B∈I(H1,H2),H=H1∪H2⊇H1∘H2.

证明(ⅰ)因为(H1∘a]H1={t∈H1|(∃k∈H1∘a)t≤k}, 所以

对任意x∈h∘j⊆H1(H1∘a]H1(j∈(H1∘a]H1), 因为H1是子超半群, 所以x∈h∘j⊆H1.由于h∘t≤h∘k, 存在y∈h∘k使得x≤y, 又因为H1是子超半群,所以y∈h∘k⊆h∘(H1∘a)⊆H1∘a.又x∈H1,x∈(H1∘a]H1，所以H1∘(H1∘a]H1⊆(H1∘a]H1.

若x≤y,x∈H1,y∈(H1∘a]H1,则存在z∈H1∘a使得x≤y≤z, 所以x≤z, 从而x∈(H1a]H1.由以上证明可得(H1a]H1∈I(H1,∅).

(ⅱ)证明过程与(ⅰ)类似.

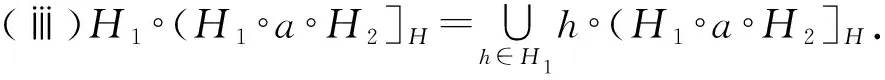
h∘k≤h∘l⊆h∘(H1∘a∘H2)⊆(H1∘a∘H2).

由于h∘k≤h∘l, 存在y∈h∘l使得x≤y,从而有x∈H,x∈(H1∘a∘H2]H.所以H1∘(H1∘a∘H2]H⊆(H1∘a∘H2]H.同理可证(H1∘a∘H2]H∘H2⊆

(H1∘a∘H2]H.

若x≤y,x∈H,y∈(H1∘a∘H2]H,则存在z∈H1∘a∘H2使得x≤y≤z, 从而x≤z，所以x∈(H1∘a∘H2]H.由以上证明可得(H1∘a∘H2]H∈I(H1,H2),a∈S.

若x≤y,x∈H,y∈(L∘R]H, 则y∈H且存在z∈L∘R, 使得x≤y≤z.因此,x≤z,x∈(L∘R]H.

(ⅴ) 若A,B∈I(H1,H2),A∩B≠∅, 则由(ⅳ)可得(A∘B]H∈I(H1,H2). 因为

H1∘(A∩B)=H1∘A∩H1∘B⊆A∩B，

(A∩B)∘H2=A∘H2∩B∘H2⊆A∩B，

且Hx≤y,y∈A∩B, 所以x∈A,x∈B.

例4令S={a,b,c,d}且在S上有超运算“∘”(表2)和序关系“≤”:

表2 S上的超运算(例4)

≤∶={(a,a),(b,b),(c,c),(d,d),(a,c),(d,b),(d,c),(a,b)}.

图3 覆盖关系(3)的哈斯图

∶={(a,b),(a,c),(d,b),(d,c)}.

(3)

令H1={b},H2={d}, 则H1,H2是S的子超半群.但H1∪H2不是S的子超半群, 因为b∘d={a,d}⊄H1∪H2(H1∘H2⊄H1∪H2).令H=H1∪H2, 则

(H1∘c∘H2]H=((b∘c)∘d]H=

({a,c,d}∘d]H=({a,d}]H={d}.

因为H1∘(H1∘c∘H2]H=H1∘{d}=b∘d={a,d}⊄(H1∘c∘H2]H, 所以(H1∘c∘H2]H∉I(H1,∅), 当然 (H1∘c∘H2]H∉I(H1,H2).

注3通过定理1和例4,我们改正了文献[10]引理2.10中的一些条件错误.

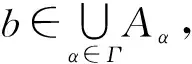
定理3令S是序超半群,H1,H2是S的子超半群,H=H1∪H2是S的子超半群且A⊆H1,B⊆H2.若A∈I(H1,∅),B∈I(∅,H2)且C∈Im(H1,H2),则对于任意c∈C,有C=(A∘c∘B]H.

证明因为A∈I(H1,∅),B∈I(H2,∅),根据引理1(ⅲ)可得

H1∘(A∘c∘B]H⊆(H1]H∘(A∘c∘B]H⊆

(H1∘A∘c∘B]H⊆(A∘c∘B]H.

类似地,可得(A∘c∘B]H∘H2⊆(A∘c∘B]H.

令x∈H,x≤y∈(A∘c∘B]H,则存在a∈A,b∈B,使得x≤y∈a∘c∘b,从而x∈(A∘c∘B]H.

另一方面,因为(A∘c∘B]H⊆(A∘C∘B]H⊆(H1∘C∘H2]H⊆(C]H=C且C∈Im(H1,H2),所以C=(A∘c∘B]H.

若A=H1,B=H2,则可得以下结论.

推论1令S是序超半群,H1,H2,H1∪H2是S的子超半群.若A∈Im(H1,H2),则对于任意a∈A,有A=(H1∘a∘H2]H.

例5令S={a,b,c,d},定义S上的一个超运算“∘”(表3)和一个序关系“≤”：

表3 S上的超运算(例5)

≤∶={(a,a)(b,b)(c,c)(d,d)(a,b)}，

则(S,∘,≤)是S中的一个序超半群.令H1={a,b,c},H2={a,c},则H1,H2和H1∪H2是S的子超半群.令A={a,b}⊆H1,B={a}⊆H2,易证A∈I(H1,∅),B∈I(∅,H2),C={a,b}∈Im(H1,H2)以及C=(A∘a∘B]H=(A∘b∘B]H.

类似于定理3的证明,易得以下两个定理.

定理4令S是序超半群,H1,H2是S的子超半群.若A∈Im(∅,H2)(A∈Im(H1,∅)), 则对于任意h2∈H2有(A∘h2]H2∈Im(∅,H2)(对于任意h1∈H1有(h1∘A]H1∈Im(H1，∅)).

定理5令S是序超半群,H1,H2,H1∪H2是S的子超半群.若A∈Im(H1,∅)且A⊆H1,B∈Im(∅,H2)且B⊆H2,则对于任意c∈S,有(A∘c∘B]H∈Im(H1,H2).

定理6令S是交换序超半群,H1,H2,H1∪H2是S的子超半群.若B⊆H=H1∪H2且A∈I(H1,H2), 则

(A∶B)={x∈S|b∘x⊆A,∀b∈B}

证明令x∈(A∶B),h1∈H1,h2∈H2,则对任意b∈B,有

b∘(h1∘x)=h1∘(b∘x)⊆h1∘A⊆A,b∘(x∘h2)=(b∘x)∘h2⊆A∘h2⊆A.

因此h1∘x,x∘h2⊆(A∶B).令b∈B,y∈(A∶B),若存在h满足h≤y,则对于任意b∈B,有b∘h≤b∘y.因为b∘y⊆A,b∘h⊆H,所以b∘h⊆A，从而h∈(A∶B).

定义7设S为一个序超半群.若对于任意a∈S,存在x∈S,使得a≤x∘a2(a≤a2∘x)，则称S为左(右)正则的.若对于任意a∈S,存在x∈S,使得a≤a∘x∘a，则称S为正则的.

对偶地,我们可以证明B也是S的右超理想.

3 展望

一般半群上相对理想的提出已超过了半个世纪,其研究者不多,近期印度学者将它们推广到序半群上并给出序半群相对理想的概念及其一系列性质,其中有很多问题都出现在序结构上.本文在已有文献的基础上将相对理想推广到序超半群，给出了序超半群上相对超理想的基本性质.这是一个大的飞跃,但还有很多问题需要进一步讨论,例如，相对超理想的序结构如何定义,会有几种方式等,将在未来的工作中进一步研究.