具有非局部边界条件的抛物型方程的爆破解
2023-01-14岳丽霞孟海霞
岳丽霞, 孟海霞
(兰州交通大学 数理学院,甘肃 兰州 730070)
本文研究具有非局部边界条件的非线性反应扩散方程解的性质:
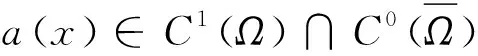

(ⅱ)a(x)>0,x∈Ω,a(x)=0,x∈∂Ω.
许多物理、化学和生物种群动力学现象都可以用具有非局部源的抛物型方程来描述, 具体可参考文献[1-8]. 例如, 方程(1)描述了一些牛顿流体通过多孔介质时的浓度扩散以及某些生物种群在迁移过程中的密度扩散. 此外, 热弹性学中的一些现象也可以抽象为具有非局部边界条件的抛物型方程. 近些年, 具有非局部反应源的抛物型方程已被广泛研究. 特别地, Song[1]利用辅助函数构造法及微分不等式技巧研究了具有Neumann和Dirichlet边界条件的非线性反应扩散方程爆破时间的上、下界. 王玉兰等[2]利用上下解方法研究了Dirichlet非局部边界条件下具有阻尼项的反应扩散方程全局解存在和不存在的条件并对爆破解的速率作了估计. Cui等[3]利用上下解方法研究了具有非局部边界条件以及非局部反应源的反应扩散方程爆破解、全局解存在的条件, 并估计了爆破速率. 刘丙辰等[4]利用上下解方法研究了Neumann非局部边界条件下具有非线性非局部源的反应扩散方程的爆破现象, 得到了该问题的解全局存在的条件、一维空间中的爆破率以及高维空间中爆破时间的上、下界.本文的主要目的是结合文献[2,4]的方法研究具有非局部反应源和非局部边界条件的问题. 具体而言, 考虑非局部非线性项、阻尼项和非局部边界对问题(1)解的影响. 由于本文研究的是与文献[2,4]不同的反应项和扩散项, 需构造完全不同的上解和下解, 利用上下解方法得到该问题的整体解和爆破解的存在性定理. 此外, 当爆破发生时, 构造新的辅助函数, 利用微分不等式技巧对爆破时间的上、下界作了估计.
1 预备知识


则称u(x,t)在有限时间内爆破.
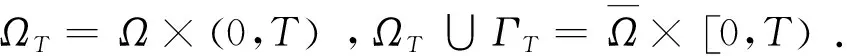
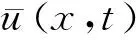
下解的定义类似于每个不等式的逆解.
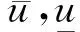


则问题(1)的解u(x,t)也一定在有限时间内爆破.
2 解的存在性
设μ和φ是特征值问题
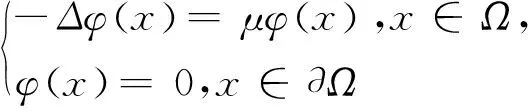
定理3若p+q 证明假设存在0<ε<1, 选择一个l, 使得 其中 则有 对于x∈∂Ω, 有 设λ和φ是特征值问题 的第一特征值及其对应的特征函数, 其中λ>0,φ>0. 引理1设v(t)是问题 的唯一解, 其中v(0)≥φ(x),则v(t)发生爆破. 定理4若p+q>s,u0(x)≥φ(x),则问题(1)存在爆破解. λφ(x)eλt-Δφ(x)eλt- 2λφ(x)eλt-a(x)φp+q(x)eλ(p+q)t+eλstφs(x)≤0. 定理5设0 由文献[5]引理2.1得 其中 由Hölder不等式得 定理6设1 由Hölder不等式得 则 由Young不等式得 所以 Φ′(t)≥ 其中 由Hölder不等式得 Φ′(t)≥M1Φp+q(t)-M2, 对上式在(0,t*)上积分可得结果.证毕. 本文研究了具有阻尼项的反应扩散方程(1)的爆破问题, 采用上下解方法得到了问题(1)整体解和爆破解的存在性定理. 将辅助函数法与微分不等式技巧相结合得到爆破时间的上、下界. 经研究发现, 问题(1)的解是全局存在还是会发生爆破取决于参数的大小.
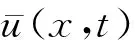
3 爆破

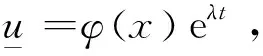

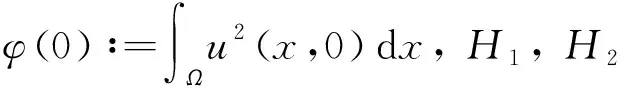





4 结论
