沂河流域山东段径流演变特征及影响因素分析

侯恩光,王如岩,张靖,谭秀翠,刘晓蓬*

沂河流域山东段径流演变特征及影响因素分析

侯恩光1,王如岩2,张靖3,谭秀翠3,刘晓蓬3*

1. 济南市水文中心, 山东 济南 250000 2. 泰安市水文中心, 山东 泰安 271018 3. 山东农业大学, 山东 泰安 271018

本文在介绍趋势检验法、突变检验法、周期分析法、双累积曲线法以及径流变化因素贡献识别法的基础上，以沂河流域山东段为研究对象，进行了径流量演变特征及影响因素分析。从径流趋势、径流突变和径流周期等方面分析了沂河流域径流量变化的历史特征；从降水趋势、降水突变和降水周期等方面分析了沂河流域降水量变化的历史特征；从不同时段径流量与降水量的变化特征、降水量和人类活动的贡献率等方面分析了引起沂河流域径流量变化的影响因素。通过本文研究可知：1956-2016年沂河流域径流量与降水量总体呈现下降趋势；相比于降水量，在各个5年时段径流量的变化幅度更大，变化效果更为显著；1965-2016年降水量对沂河流域径流量增大的贡献率为61.76%，而人类活动的贡献率为38.24%。本文研究表明人类活动对沂河流域径流量的增大造成了较大影响。

沂河流域; 径流量; 降水量

随着人类活动对气候变化的影响日益增大，降水分布和植被生长状况也随之发生了明显变化，从而间接对河川径流造成了显著影响[1]。河川径流是水循环中的一个基本环节，对人类生产活动和自然生态平衡稳定起到非常重要的作用[2]。已有研究表明，目前全球大多数河流的径流量正逐渐向总体减少的趋势发展，这是对全球水安全的巨大威胁和挑战[3]。在人类活动日益加剧的背景下，研究人类活动对河川径流演变的影响十分必要。因此，针对影响地区发展的重要河流进行径流演变特征分析，找出河川径流变化的影响因素具有非常重要的现实意义。

对于当前的河川径流演变情况，已经有很多相关领域的专家学者做了一些有意义的探索研究，以寻找气候变化和人类活动与河川径流变化之间的关系。孙洋洋等研究了黄河中上游地区径流量格局的长期变化过程，结果表明该区域的径流量呈显著减少的趋势[4]。张海荣等基于单、多变量的M-K趋势分析法和突变检验法对金沙江流域降水量和径流量的时空演变情况进行了非一致性分析，结果表明该流域降水量和径流量呈现总体上升的趋势[5]。潘扎荣等基于M-K法和累积距平法，定量和定性分析了淮河干流径流量实测值年际变化的趋势性与阶段性，结果表明淮河干流径流量呈现总体下降的趋势[6]。TAO等采用M-K法和累积距平法判断塔里木河流域降水量和径流量的突变时间，重点分析了降水量与人类活动对该流域径流量变化的贡献率问题，由此得出结论为：降水量对塔里木河流域径流量变化的影响程度在逐渐降低，而人类活动对塔里木河流域径流量变化的影响程度在逐渐增大[7]。宋小燕等基于M-K检验法和累积距平法分析了松花江流域哈尔滨站近100年的径流量变化趋势，结果表明松花江流域径流量未表现出显著的趋势性特征[8]。郭爱军等采用滑动偏相关系数法、双累积曲线法和Copula函数，诊断分析并验证了泾河流域降水量与径流量关系的变化特征和变异情况，结果表明人类活动对泾河流域径流量减少的贡献率是气候变化的4倍以上[9]。刘昌明等基于黄河84个子流域1956-2016年的气象水文资料，回顾了黄河流域径流及其影响因素的时空变化特征，分析了径流变化的可能原因和区域差异[10]。姬世保等构建了密云水库上游流域二元分布式水文模型，设置了多个情景对流域水循环过程进行模拟，并在此基础上使用多因素归因分析法对河川径流演变进行了定量归因[11]。阳扬等选用集总式水文模型MODHYDROLOG模拟漓江流域2008-2016年的日径流量，在不同时段人类活动和气候变化情景下分析了土地利用类型与模型时变参数的相关性，揭示了流域降水-径流特征的变化情况，对流域特征受人类活动影响的动态定量感知进行了探索[12]。

本文基于沂河流域山东段（以下简称“沂河流域”）1956-2016年的径流量和降水量等基础数据资料，采用M-K法对径流量和降水量进行了变化趋势的显著性检验分析；采用Pettitt法、有序聚类法、Lee-Heghinan法对径流量和降水量进行了突变检验分析；采用Morlet小波法对径流量和降水量进行了周期性检验分析；通过分析不同时段年均降水量、年均径流量的变化特征，明确降水量变化与人类活动对径流变化的影响；通过建立降水量-径流量双累积基准关系式，分析得到降水量变化和人类活动对径流量变化影响量的贡献程度。综上，本文研究可为流域水库调度、水量优化配置和水资源安全保障等重大事项提供参考依据和科学指导。

1 研究区域概况

沂河源出山东省沂源县田庄水库，流经淄博市（流域面积为1 444 km2）、临沂市（流域面积为9 563 km2），最终从江苏省汇入黄海，全长为386 km，流域总面积为11 600 km2，其中山东省境内河长为287.5 km，流域面积为11 007 km2。本研究以沂河流域1956-2016年径流量和降水量等基础数据资料为研究对象。沂河流域山东段具体地理位置如图1所示。

图 1 沂河流域山东段地理位置图

2 研究方法

在水文学中，对降水量和径流量的研究主要包括趋势性分析、突变点检验、周期性分析等，其所检验要素之间相互独立，而亦可互为参考。趋势性分析中最常用的是Mann-Kendall检验法；突变点检验中常用的方法包括Pettitt法、有序聚类法和Lee-Heghinan法，三种方法各有特点且可相互验证；周期性分析中，通常应用Morlet小波分析法。为了更加明确探究降水量与径流量之间的相互关系及人类活动对河川径流的影响，通常采用双累积曲线进行辅助分析，并以此判别降水量变化和人类活动对河川径流量变化的影响量贡献率。

2.1 趋势检验法

Mann-Kendall检验法是水文研究中最常用的趋势性检验方法，简称为M-K法。M-K法受异常数据干扰的概率相对较小，而且该方法不受样本序列的影响，尤其适用于对水文、气象时间序列变化趋势的检验分析[7]。利用M-K法对样本数值进行趋势变化显著性检验时，应首先假设样本序列无显著性趋势变化，然后再进行两尾检验。当显著性水平已知时，临界值1-ɑ/2可以通过查正态分布表得到。当||<1-ɑ/2时，则接受该样本序列无显著性趋势变化的原有假设，而当||≥1-ɑ/2时，则拒绝原有假设，也即是认为该样本序列有显著性趋势变化。||与样本序列变化趋势的显著性呈正相关关系，当>0时，表明该样本序列呈上升趋势，当<0时，表明该样本序列呈下降趋势。

2.2 突变检验法

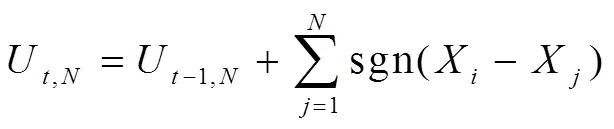
式（1）的实际意义为：统计样本序列中序列号在前的样本值大于紧邻其后的样本值的总个数。X和X分别表示总数为的某时间样本序列上的不同样本值，表示某一样本值的序列号。

当U,N达到最大值时，则其所对应的时间点0即为该样本序列的突变点。突变点位置表达式为：

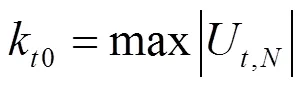
可以通过建立统计量来判断上述突变点的显著性水平，的表达式为：

若计算所得统计量小于预先假设的显著性水平，则可以认为通过Pettitt法得到的突变点在统计意义上发生了显著性变化。

2.2.2 有序聚类法有序聚类法是一种数学统计方法，建立该方法的目的是寻找样本序列的最优分割点。有序聚类法的实质是：首先对所需检验的样本序列进行分割并得到各分割点，之后分别计算分割点前与分割点后各子序列的离差平方和，当总离差平方和取最小值时，即认为该最小值所对应的分割点为该样本序列的最优分割点[14]。在水文学中，利用有序聚类法可以确定水文要素中的突变点。有序聚类法的计算公式为：

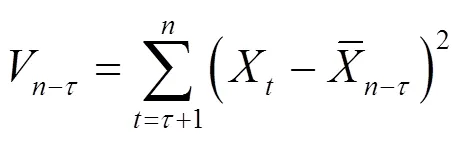
2.3 周期分析法

Morlet小波分析是探究样本序列多时间尺度特点的常用方法，Morlet小波变换在时域和频域同时具有良好的局部性，从而能够清晰显现各时间尺度的分布与强弱。小波的实部系数可以反映样本序列的周期和振幅，小波方差图可以判别不同时间尺度的干扰强度，找出样本序列的主周期。

在水文学中，利用Morlet小波分析可以实现对某流域径流量和降水量序列的周期性检验。Morlet小波变换图可以反映规定年份内径流量和降水量在不同时间尺度上的周期震荡，而信号的强弱则是通过小波系数的大小进行表示。小波光谱图中，通常用颜色深度代表径流量或降水量偏离其多年平均值的程度，颜色越深表示偏离程度越高；红色代表径流量或降水量偏高，蓝色代表径流量或降水量偏低；当小波系数为零时则对应着径流量或降水量的突变点。

2.4 双累积曲线

将相同历史时期内因变量与自变量各自随时间的连续累积值之间的关系曲线在直角坐标系中表示出来的方法称为双累积曲线法。该方法能够通过消除参考变量的影响而达到鉴别影响因素是否会导致被检验变量发生了显著趋势性变化的效果。在长序列水文要素的演变趋势分析中，双累积曲线法因操作简单且直观易懂而得到最为广泛的应用[15-18]。对于降水量和径流量的时间累积值，当研究时间的序列长度有限时，降水量的变化是自然发生的，也即可以认为人类活动对降水量的影响相对较小，而径流量的变化受降水量和人类活动的共同影响。因此，基于径流量M-K检验结果和降水量-径流量双累积曲线统计模型进行径流量变化影响因素分析时，通常将降水量作为参考变量拟合降水量-径流量双累积曲线的基准关系式，结合降水量和径流量在突变年份前后的变化特点，共同模拟降水量和径流量的年际演变过程，以此判别降水量变化与人类活动对河川径流量变化的影响程度。

2.5 径流变化因素贡献识别

降水量-径流量双累积曲线是识别径流变化因素贡献率的重要基础。根据参考文献[15]可知，基于降水量-径流量双累积曲线，通过判别突变年份前、后两个阶段径流量实测值与理论值之间的关系，可以得出降水量变化和人类活动所导致的径流量变化值[15]，具体如下式所示：

δ=R2-R1(8)

δ=R2-R2(9)

式中：表示由于降水量变化所导致的径流量变化值，表示由于人类活动所导致的径流量变化值，R1表示突变年份之前的实测平均径流量，R2表示突变年份之后的实测平均径流量，R2表示突变年份之后的理论平均径流量。

基于突变年份之前的降水量-径流量双累积曲线基准关系式，可以得到降水量变化对径流量的影响量理论值，将其与径流量的实测平均值进行差值计算，以此定量分析降水量变化和人类活动对径流量变化的影响程度，并分别得到降水量变化和人类活动对径流量变化的影响量贡献率[15]。影响量贡献率的表达式为：Q=δ/R×100% (10)

Q=δ/R×100% (11)

式中：Q表示降水量变化对径流量变化的影响量贡献率；Q表示人类活动对径流量变化的影响量贡献率；R表示突变年份之前和之后的两个阶段径流量实测平均值之差，即降水量变化和人类活动所引起的径流量变化值。

3 沂河流域径流量影响因素分析

径流量变化的主要影响因素主要包括自然降水、气候变化和人类活动等。气候变化所导致的高山融水对沂河流域径流量的影响可以基本排除，但是径流量变化不能忽视人类活动的影响，因此在分析过程中重点考虑降水因素和人类活动对沂河流域径流量的影响。趋势检验法、突变检验法、周期分析法是分析沂河流域径流量和降水量趋势性、突变性和周期性特征的基本方法；沂河流域不同时段年均降水量、年均径流量的变化特征是判别其径流量与降水量阶段性变化趋势的重要依据；基于降水量-径流量双累积曲线，可准确识别降水量变化和人类活动对沂河流域径流量变化的影响量贡献率。

3.1 径流量特征分析

3.1.1 径流量趋势分析沂河流域的径流量变化特征如图2所示，M-K统计检验结果如图3所示。

图2中，1956-2016年沂河流域径流量年际变化的趋势线斜率为-0.2014，总体呈现下降趋势，但因斜率绝对值较小，故下降趋势并不明显。1956-1976年沂河流域径流量的变化幅度较大，而1976-1989年则相对平稳，但其下降趋势仍然不可忽视，且在1989年达到了1956年以来的径流量最小值。1976-2016年沂河流域径流量总体呈现上升趋势，其中1989-2012年的上升趋势最为显著，趋势线斜率为0.2078。2012年之后，沂河流域径流量开始呈现下降趋势，但因为统计标本量过少，这种趋势并不具有广泛的现实意义。

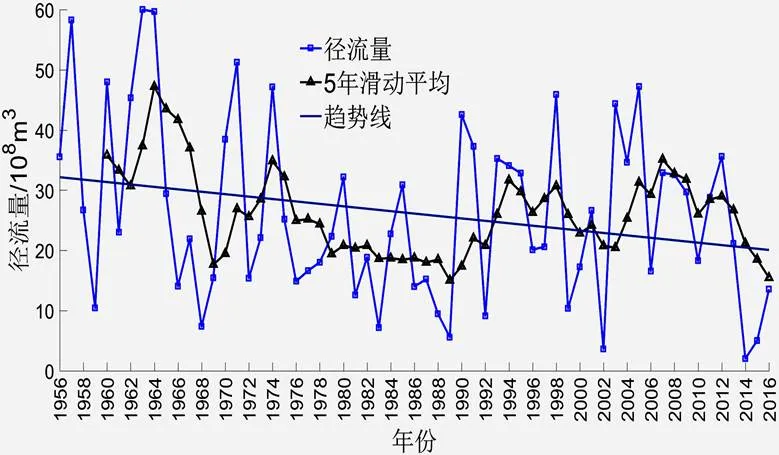
图 2 沂河流域径流量变化特征图

图 3 沂河流域径流量M-K统计检验

图3中，沂河流域径流量在1986-1994年和2002-2005都出现了短暂的显著性上升趋势变化，这与1956-2016年沂河流域径流量呈现总体下降趋势的结论相冲突，但与1976-2016年沂河流域径流量呈现总体上升趋势的结论相吻合。

3.1.2 径流量突变分析由M-K统计检验结果可知，沂河流域径流量在1965年出现了突变，1965-2000年总体呈现下降趋势；在2002年再次出现了突变，2002-2012年总体呈现上升趋势；在2012年之后呈现短期下降的态势。

对1956-2016年沂河流域径流量Pettitt检验，找出突变年份，再以突变年份为分割点对不同时段的径流量进行Pettitt检验，分别得到其突变年份、变异年所对应的k0值以及统计量值（表1）。

表 1 沂河流域不同时段径流量Pettitt检验结果

表1中，统计量值均小于预先设定的显著水平=0.05即1.96，则可以认为通过Pettitt检验得到的突变点在统计意义上发生了显著性变化。

通过有序聚类法对1956-2016年沂河流域径流量进行分析可知，沂河流域径流量在1965年和1989年发生了突变，所得总离差平方和的最小值为14093.1。采用Lee-Heghinan法对沂河流域径流量进行分析可知：1956-2016年的分割点年份为1965年，1965-2016年的分割点年份为1989年。

基于以上两个突变点分别计算不同时段的沂河流域径流量平均值，具体如表2所示。

表 2 突变年份前后不同时段沂河流域径流量平均值

综合以上Pettitt检验、有序聚类法、Lee-Heghinan法的检验结果及表2中突变年前后的径流量平均值变化率结果可以看出，沂河流域径流量最重要的突变点为1965年，其次是1989年。

3.1.3 径流量周期分析沂河流域径流量的小波变换实部图如图4，小波方差结果如图5所示，由此可直观知晓该流域径流量的周期性变化特征。

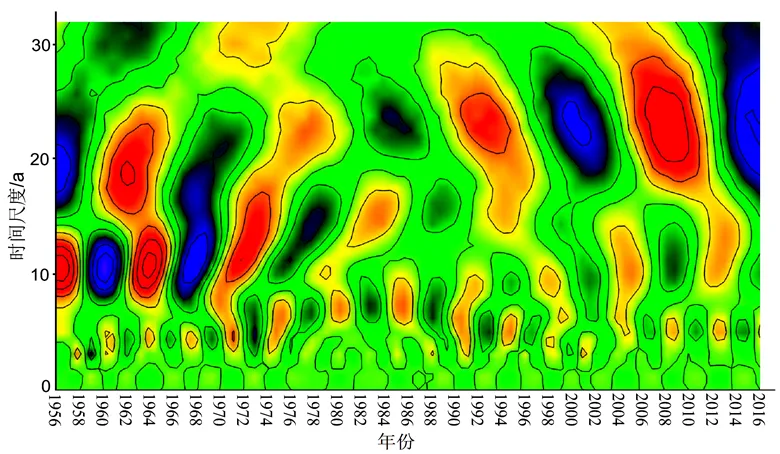
图 4 沂河流域径流量小波变换实部图

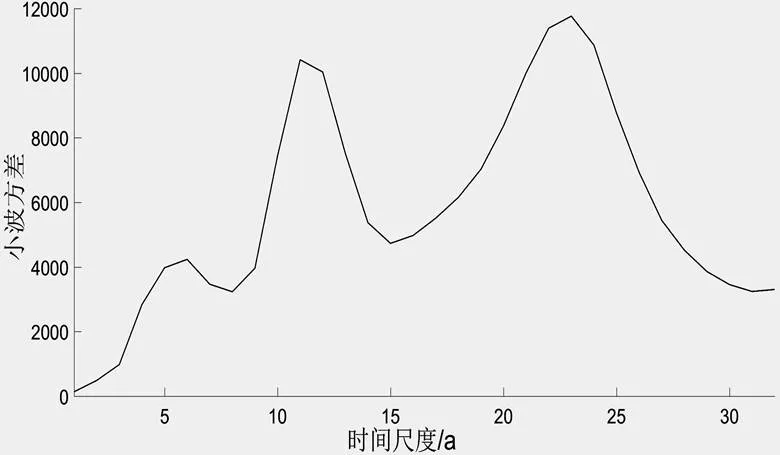
图 5 沂河流域径流量小波方差图

图4中，红色向蓝色的过度代表了丰水期向枯水期的演变。沂河流域的径流量演化过程表现出多个时间周期尺度，总体表现为16-32年、8-15年和3-7年时间尺度的周期性变化规律。在16-32年时间尺度上表现出丰水年与枯水年的准两次周期性震荡，且主要产生于1986年之后；在8-15年时间尺度上表现出准三次周期性丰枯震荡，且主要产生于1984年之前；16-32年和8-15年时间尺度的周期性变化相对于1956-2016年的分析时段，表现出了不稳定性的特征。3-7年时间尺度的周期性变化规律在1972-1996年表现得较为稳定。

由图5可知，沂河流域径流量小波方差的3个峰值由大到小依次对应23年、11年和6年的时间尺度，整体描述了径流量1956-2016年的周期性变化规律，分别对应第1、第2和第3主周期。

3.2 降水量特征分析

3.2.1 降水量趋势分析1956-2016年沂河流域的多年平均降水量为794.17 mm，其变化特征如图6所示。降水量总体呈现下降趋势，趋势线斜率的绝对值为1.9256。1956-1976年降水量变化幅度较大，1976-1988年则相对平稳，但下降趋势仍然不可忽视，且在1988年达到了1956年以来的最小值。1989-2012年沂河流域降水量总体呈现上升趋势，趋势线斜率为1.7196，因斜率值较小，故上升趋势并不明显。2012年之后沂河流域降水量开始呈现下降趋势，但因为统计标本量过少，这种趋势并不具有广泛的现实意义。沂河流域降水量M-K统计检验如图7所示，由此可知，沂河流域降水量在1964年出现了突变，且在1965年之后总体呈现下降趋势。

图 6 沂河流域降水量变化特征

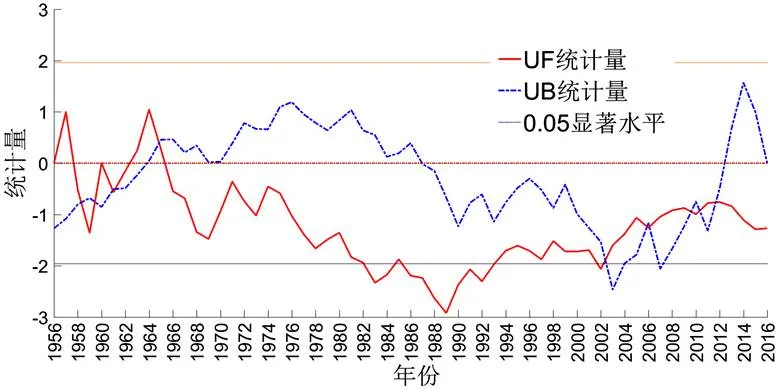
图 7 沂河流域降水量M-K统计检验

通过对比沂河流域径流量与降水量的趋势性变化特征可以看出，1956-2016年沂河流域径流量和降水量都呈现总体下降趋势；相关性分析可知径流量变化受降水量变化影响明显，达到0.9271。但是径流量的变化具有明显的滞后性，这与径流主要来源于降水的自然规律是吻合的。

3.2.2 降水量突变分析通过对1956-2016年沂河流域降水量进行Pettitt检验可得，沂河流域降水量突变点分别为1964年和1989年，所对应的统计量值分别为0.2178和0.5549，均小于预先设定的显著水平=0.05即1.96，则可以认为突变点在统计意义上发生了显著性变化。通过有序聚类法可得，沂河流域降水量突变点分别为1964年和1989年。通过Lee-Heghinan法可得，沂河流域降水量的最大统计值为-29.5，分割点年份确定在1964年。

基于以上两个突变点分别计算不同时段的沂河流域降水量平均值，具体如表3所示。

表 3 突变年份前后不同时段沂河流域降水量平均值

通过对突变年份前后两个时段内沂河流域径流量平均值与降水量平均值变化率的比较分析可知，降水量的变化率明显比径流量的变化率小得多，这间接说明了人类活动对沂河流域径流量的变化产生了重要影响。

综合以上Pettitt检验、有序聚类法、Lee-Heghinan法的检验结果及表3中突变年前后的降水量平均值变化率结果可知，沂河流域降水量最重要的突变点为1964年，其次为1989年。

3.2.3 降水量周期分析沂河流域降水量的小波变换实部图如图8，小波方差如图9所示。由此可知，沂河流域降水量在1956-1969年、1970-1989年和1990-2016年分别以10-12年、14-18年和20-30年的时间尺度呈周期性变化。小波方差的3个峰值由大到小依次对应23年、11年和7年的时间尺度，描述了降水量在整个时段内的周期性变化规律，并分别对应第1、第2和第3主周期。

图 8 沂河流域降水量小波变换实部图

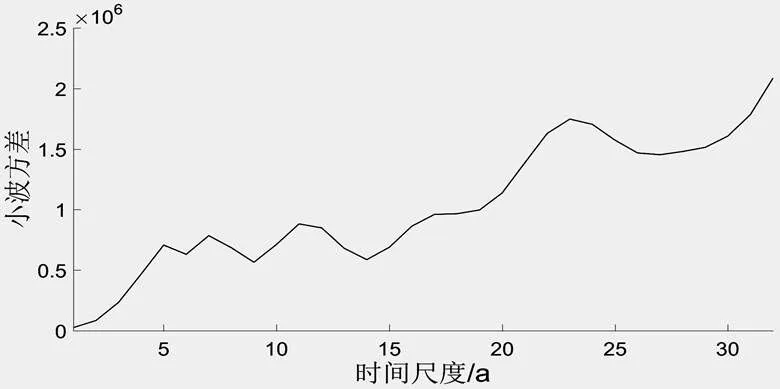
图9 沂河流域降水量小波方差图

通过对比沂河流域径流量与降水量的周期性变化规律可以看出，径流量与降水量的周期性变化规律基本吻合，但又并非完全吻合，这说明沂河流域的径流量变化还受其他因素的影响。

3.3 不同时段年均降水量、年均径流量变化特征

为更明确沂河流域降水量与人类活动对径流变化的影响，以5年时间段为单位对其分析（表4）。

表 4 沂河流域不同时段年均降水量、年均径流量变化特征

由表4可知，沂河流域各个5年时段的平均降水量和平均径流量最大值均发生在1961-1965年时段，分别为943.32 mm和43.496×108m3；最小值均发生在1986-1990年时段，分别为678.76 mm和17.368×108m3。在1986-1990和2001-2005年这两个时段的降水量变化相对最为显著，1986-1990年时段的极值比为1.184，变差系数为0.318，变差系数为各时段的最大值；2001-2005年时段的极值比为1.625，变差系数为0.289，极值比为各时段的最大值。根据径流量的极值比和变差系数统计结果，1986-1990年时段的变差系数为0.752，极值比为6.62，变差系数为各时段的最大值；2011-2016年时段的径流量极值比为16.537，变差系数为0.289，极值比为各时段的最大值。综合比较后可以发现，在各个5年时段径流量的极值比和变差系数均比降水量的大，说明该流域径流量与降水量的变化趋势并非完全一致，径流量的变化幅度更大且变化效果更为显著，这间接表明了人类活动是引起该流域径流量变化的一个重要影响因素。

3.4 降水量-径流量双累积曲线与基准关系式

根据前文的统计检验结果，沂河流域降水量最重要的突变点为1964年，其次是1989年，但是由于1956-1964年数据量过少，为能够更加明确降水量和人类活动对沂河流域径流量的影响，特选定1965-2016年的降水量和径流量对其进行定量分析，分割点为1989年。1965-2016年的降水量和径流量的M-K统计检验结果分别如图10和图11所示，由此可知1989年为1965-2016年时段降水量和径流量的最重要突变点。建立1965-1988年降水量与径流量的双累积曲线，可得其基准关系式为=0.0302+3.7048，降水量和径流量双累积曲线拟合相关程度2值为0.9962，如图12所示。根据沂河流域的原始实测数据，1965-1988年的径流量多年实测平均值为21.787×108m3，而通过基准关系式计算得到的多年平均径流量理论值为22.5×108m3，理论值与实测值之间的绝对误差为0.713×108m3，相对误差为3.27%，这表明基准关系式的拟合精度较高，有较高的可信度。

图 10 沂河流域1965-2016年降水量M-K统计检验

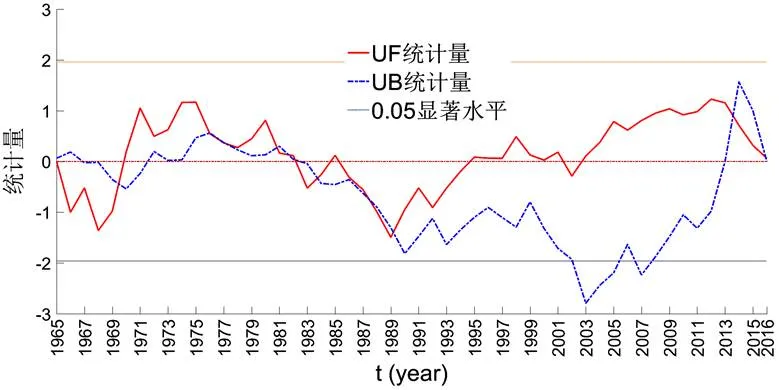
图 11 沂河流域1965-2016年径流量M-K统计检验

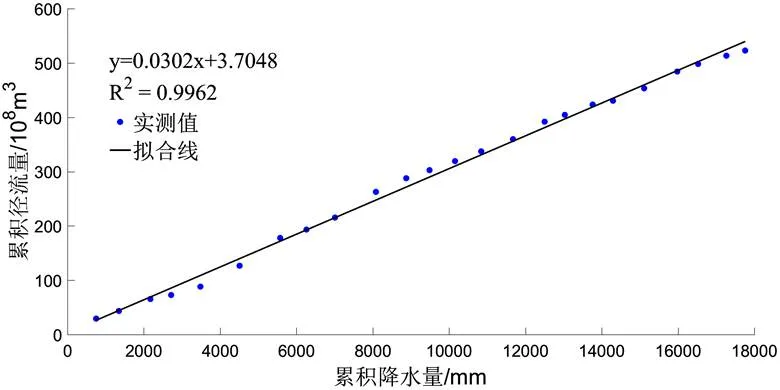
图 12 沂河流域1965-1988年实测累积值拟合线

图 13 沂河流域1989-2016年理论值和实测值拟合线

将突变年份之后（1989-2016年）的累积降水量代入到基准关系式=0.0302+3.7048中，即得对应年份的累积径流量理论值。分别绘制1989-2016年沂河流域降水量与实测径流量的双累积曲线和降水量与理论径流量的双累积曲线，如图13所示。通过理论值累积量拟合线与实测值累积量拟合线的对比可知，除了降水量对沂河流域径流量的变化有显著影响之外，人类活动有使沂河流域径流量增大的趋势，而且人类活动的影响相对较为显著。

3.5 降水量和人类活动的贡献识别

将1965-2016年沂河流域的累积降水量代入到基准关系式=0.0302+3.7048中，即可得到对应年份的累积径流量，然后通过反推计算可以得到该时段中每一年的径流量理论值。分别计算突变年份之前（1965-1988年）和之后（1989-2016年）两个时段的实测平均径流量和理论平均径流量，即可分别得到因降水量和人类活动影响而各自产生的径流影响量。突变年之前沂河流域的实测平均径流量为21.787×108m3，理论平均径流量为22.5×108m3；突变年之后沂河流域的实测平均径流量为25.134×108m3，理论平均径流量为23.854×108m3。具体如表5所示。

表 5 降水量和人类活动对沂河流域径流量影响的统计值

由表5可知，降水量对沂河流域径流量增大的影响量为2.067×108m3，贡献率为61.76%，而人类活动的影响量为1.28×108m3，贡献率为38.24%，故由此可以量化得出人类活动对沂河流域径流量增大造成了较大的影响。

4 结 论

（1）沂河流域1956-2016年径流量总体呈现下降趋势；1965年为径流量的最重要突变点，其次为1989年；23年、11年和6年分别对应径流量变化的第1、第2和第3主周期；

（2）沂河流域1956-2016年降水量总体呈现下降趋势，1964年为降水量的最重要突变点，其次为1989年；在1956-1969年、1970-1989年和1990-2016年分别以10-12年、14-18年和20-30年的时间尺度呈周期性变化，23年、11年和7年分别对应降水量变化的第1、第2和第3主周期；

（3）在各个5年时段沂河流域径流量的极值比和变差系数均比降水量的大，径流量与降水量的变化趋势并非完全一致，径流量的变化幅度更大且变化效果更为显著；

（4）沂河流域径流量和降水量在1965-2016年的最重要突变点为1989年；降水量和人类活动对该流域径流量增大的贡献率分别为61.76%和38.24%，由此可量化表明人类活动对沂河流域径流量增大造成了较大的影响。

[1] Zhang HX, Zhang L, Zhu RR,. Responses of streamflow to climate and land surface change in the headwaters of the Yellow River Basin [J]. Water Resources Research, 2009,45(7):641-648

[2] 孙琪,徐长春,任正良,等.塔里木河流域产水量时空分布及驱动因素分析[J].灌溉排水学报,2021,40(8):114-122

[3] Wang SJ, Yan M, Yan YX,. Contributions of climate change and human activities to the changes in runoff increment in different sections of the Yellow River [J]. Quaternary International, 2012,282:66-77

[4] 孙洋洋,穆兴民,高鹏,等.黄河上中游区径流量格局长期变化过程[J].水土保持研究,2017,24(3):59-64

[5] 张海荣,周建中,曾小凡,等.金沙江流域降水和径流时空演变的非一致性分析[J].水文,2015,35(6):90-96

[6] 潘扎荣,阮晓红,朱愿福,等.近50年来淮河干流径流演变规律分析[J].水土保持学报,2013,27(1):51-55,59

[7] Tao H, Gemmer M, Bai Y,. Trends of stream-flow in the tarim river basin during the past 50 years: human impact or climate change [J]. Journal of Hydrology, 2011,400(1/2):1-9

[8] 宋小燕,穆兴民,高鹏,等.松花江哈尔滨站近100年来径流量变化趋势[J].自然资源学报,2009,24(10):1803-1809

[9] 郭爱军,畅建霞,王义民,等.近50年泾河流域降雨-径流关系变化及驱动因素定量分析[J].农业工程学报,2015,31(14):165-171

[10] 刘昌明,王恺文,王冠,等.1956-2016年黄河流域径流及其影响因素的变化分析[J].人民黄河,2022,44(9):1-5,16

[11] 姬世保,杜军凯,仇亚琴,等.基于二元水循环模拟的密云水库上游流域河川径流演变归因分析[J].水利水电技术(中 英文),2022,53(4):116-127

[12] 阳扬,翟禄新,贾艳红,等.不同土地利用方式下漓江流域降水-径流特征变化分析研究[J].中国农村水利水电,2022(8):97-105

[13] 吴子怡,谢平,桑燕芳,等.水文序列跳跃变异点的滑动相关系数识别方法[J].水利学报,2017,48(12):1473-1481,1489

[14] 刘茜,王延贵.江河水沙变化突变性与周期性分析方法及比较[J].水利水电科技进展,2015,35(2):17-23

[15] 胡彩虹,王艺璇,管新建,等.基于双累积曲线法的径流变化成因分析[J].水资源研究,2012,1(4):204-210

[16] 穆兴民,张秀勤,高鹏,等.双累积曲线方法理论及在水文气象领域应用中应注意的问题[J].水文,2010,30(4):47-51

[17] 张琳,马敬旭,张倩,等.近60多年洞庭湖水沙演变特征及其与人类活动的关系[J].长江科学院院报,2021,38(9):14-20

[18] 杨思雨,姜仁贵,解建仓,等.渭河上游径流变化特征及归因研究[J].水资源与水工程学报,2019,30(2):37-42

Analysis of Runoff Evolution Characteristics and Influencing Factors in Shandong Section of Yihe River Basin

HOU En-guang1, WANG Ru-yan2, ZHANG Jing3, TAN Xiu-cui3, LIU Xiao-peng3*

1.250000,2.271018,3.271018,

Based on the introduction of trend test method, mutation test method, period analysis method, double cumulative curve method and runoff change factor contribution identification method, this paper takes the Shandong section of the Yihe River Basin as an example, analyzing the runoff evolution characteristics and influencing factors. The historical characteristics of runoff changes in the Yihe River Basin have been analyzed from the aspects of runoff trend, runoff mutation and runoff cycle. The historical characteristics of precipitation changes in the Yihe River Basin are analyzed from the aspects of precipitation trend, sudden change of precipitation and precipitation cycle. The influencing factors of the runoff change in the Yihe River Basin are analyzed from the variation characteristics of runoff and precipitation in different periods, and the contribution rate of precipitation and human activities. According to the research in this paper, from 1956 to 2016, the runoff and precipitation showed a decreasing trend. Compared with precipitation, the runoff has a greater range of changes in each 5-year period, and the effect of the change is more significant. The contribution rate of precipitation to the increase of runoff in the Yihe River Basin from 1965 to 2016 was 61.76%, and the contribution rate of human activities was 38.24%. It shows that human activities have a great impact on the increase in runoff of the Yihe River Basin.

Yihe River Basin; runoff; precipitation

P461+.5

A

1000-2324(2022)06-0947-09

2022-08-11

2022-10-02

山东省自然科学基金(ZR2020QE286)

侯恩光(1980-),男,本科,高级会计师,从事水文水资源领域的研究. E-mail:houeg@163.com

Author for correspondence. E-mail:liuxiaopenglw@sdau.edu.cn

10.3969/j.issn.1000-2324.2022.06.022