A-DDPG：多用户边缘计算系统的卸载研究

曹绍华，姜佳佳，陈 舒，詹子俊，张卫山

中国石油大学（华东）计算机科学与技术学院，山东 青岛 266580

近年来，物联网（IoT）得到了快速发展，移动设备的应用也日渐复杂，需要更强的计算能力来执行任务，从而保证体验质量（QoE）和服务质量（QoS）。但是，移动设备的计算能力和电池容量是有一定限度的，如何解决资源有限的问题成为了一个重要的挑战，而移动边缘计算（mobile edge computing，MEC）为解决这个问题提供了有效途径[1]，它通过将计算任务卸载到边缘服务器上执行，从而降低移动设备的任务执行时间和能耗的总成本。但由于硬件成本等约束导致MEC服务器计算资源有限的问题日益突出，因此如何设计比较合理的卸载策略是一项重要的挑战。

计算卸载的策略有很多种[2]，然而，绝大多数计算卸载算法都认为用户设备（UE）是静止的[3]。但是，在实际应用场景中，UE通常处于移动状态，边缘服务器和UE之间的距离随着时间的变化而动态改变，这意味着UE需要动态决定是否进行卸载以及卸载到哪个边缘服务器能够在UE移动时最大化任务完成数量，同时最小化UE的总成本。

目前大多数卸载算法都假设UE拥有相同的性能，而UE在实际应用场景中不完全相同[4]。当任务维度过高时，卸载决策的二元属性导致直接枚举所有的卸载决策方案在计算复杂度上是指数级的。由于强化学习（RL）主要用于解决决策问题，所以目前大多数文章在MEC网络环境下针对离散动作空间[5]并且利用深度Q网络（DQN）来解决计算卸载问题[6-7]。然而，DQN的表格搜索属性不适合处理高维空间。因此，本文设计了一种基于DDPG的计算卸载算法，该算法可以有效地支持由于UE移动性而产生的计算卸载连续动作空间，以及任务迁移（由于MEC服务器的资源有限性）。

1 相关工作

近几年来，国内外学者对多用户MEC系统中的计算卸载进行了深入研究。文献[8]提出了一种基于博弈论的分布式任务卸载方案，在降低能耗的同时使用户之间的博弈达到纳什均衡状态。文献[9]分别通过动态改变电压频率缩放和数据传输速率来最小化单用户MEC系统的能耗。文献[3]提出了一种单用户MEC系统的延迟优化任务调度算法。文献[5]提出了一种基于交替最小化的低复杂度次优算法，借助流水车间调度理论，得到最优的任务卸载调度（即确定卸载顺序），以最小化延迟和能耗的加权和。

但上述文献都只考虑能耗或延迟一个指标，单用户或单MEC服务器系统，对此做出了一定改进，通过联合优化移动用户的资源分配决策和CPU频率，提出了一种多服务器多用户MEC系统的分布式算法，将任务卸载和资源分配结合在一起，为延迟和能耗设置权重值，使移动用户的总成本最小化。上述文献中的算法采用的假设还存在一些局限性。由于小蜂窝网络中的频谱复用，小区间的干扰对服务质量至关重要[10-11]。如果太多的移动用户同时选择相同的无线信道来卸载计算任务，可能会对彼此造成严重干扰，从而降低数据传输速率并增加能量消耗，而上述算法均忽略了小区间会产生干扰的情况。

目前基于DRL的MEC任务卸载决策的研究有许多。例如，文献[12]使用DRL解决MEC环境下车辆的任务卸载调度问题，以最小化长期卸载成本。文献[13]提出了一种基于deep Q-learning（DQN）的算法来解决多用户共享边缘网络计算资源的卸载决策问题。但是，这些基于价值的强化学习方法主要应用于离散动作。然而，简单地将连续的动作空间离散化并使用基于值函数是不可行的，因为离散化会导致性能下降。为了克服上述挑战，本文采用DDPG算法，它可以同时解决离散和连续动作问题，每一步都会更新模型权重，模型可以适应动态环境，并且利用先前的研究经验可以更好地学习，另一方面，连续状态下的算法以时间差异的方式采取措施来选择具有学习价值的动作，从而提高卸载效率。在计算卸载模型中，同时考虑计算延迟、能耗和任务失败率的工作很少，而本文提出的模型同时关注了这三个指标和用户的移动性以及MEC服务器性能的不同，以更好地提高用户的服务质量。

本文的主要贡献可以概括如下：

（1）更现实的优化目标设定。在现实生活中，终端设备的类型并不相同，仅考虑一个方面无法保证用户之间的公平性。因此，考虑了时延和能耗，并设置了权重值，制定的优化目标是在不超过任务最大可容忍延迟要求的情况下最小化用户的总成本。

（2）MEC系统的任务卸载问题定义。定义了任务卸载问题。该问题考虑了多服务器、多用户、用户的移动性、任务的等待时间以及边缘服务器性能的不同，旨在最小化用户的预期成本（考虑到MEC服务器资源的有限性，任务可以迁移）。

（3）基于DDPG的卸载算法实现。为了实现用户的预期成本最小化，提出了一种基于DDPG的分布式卸载算法A-DDPG，使每个移动设备能够进行动态卸载，并选择合适的目标MEC服务器和任务卸载量。结合了LSTM、DDPG和Attention去优化算法中成本估计。

2 系统模型

2.1 网络模型

移动边缘计算系统模型如图1所示。考虑多个基站覆盖范围内的多服务器多用户MEC系统模型，UE每隔一段时间∇可以进行相应的移动。MEC系统中有n个用户，表示为N={1,2,…,n}，MEC服务器有m个，表示为M={1,2,…,m}，一个基站服务、一个MEC服务器，这些移动用户通过动态计算和每个MEC服务器的距离远近来决定卸载目标。本文中，OFDMA（正交频分多址）用于移动用户任务卸载到MEC服务器的上行链路通信，每个移动用户共享整个带宽的通用频率[14]。在OFDMA中，可用频谱被划分为K个子信道，这些子信道的索引是K={1,2,…,k}。

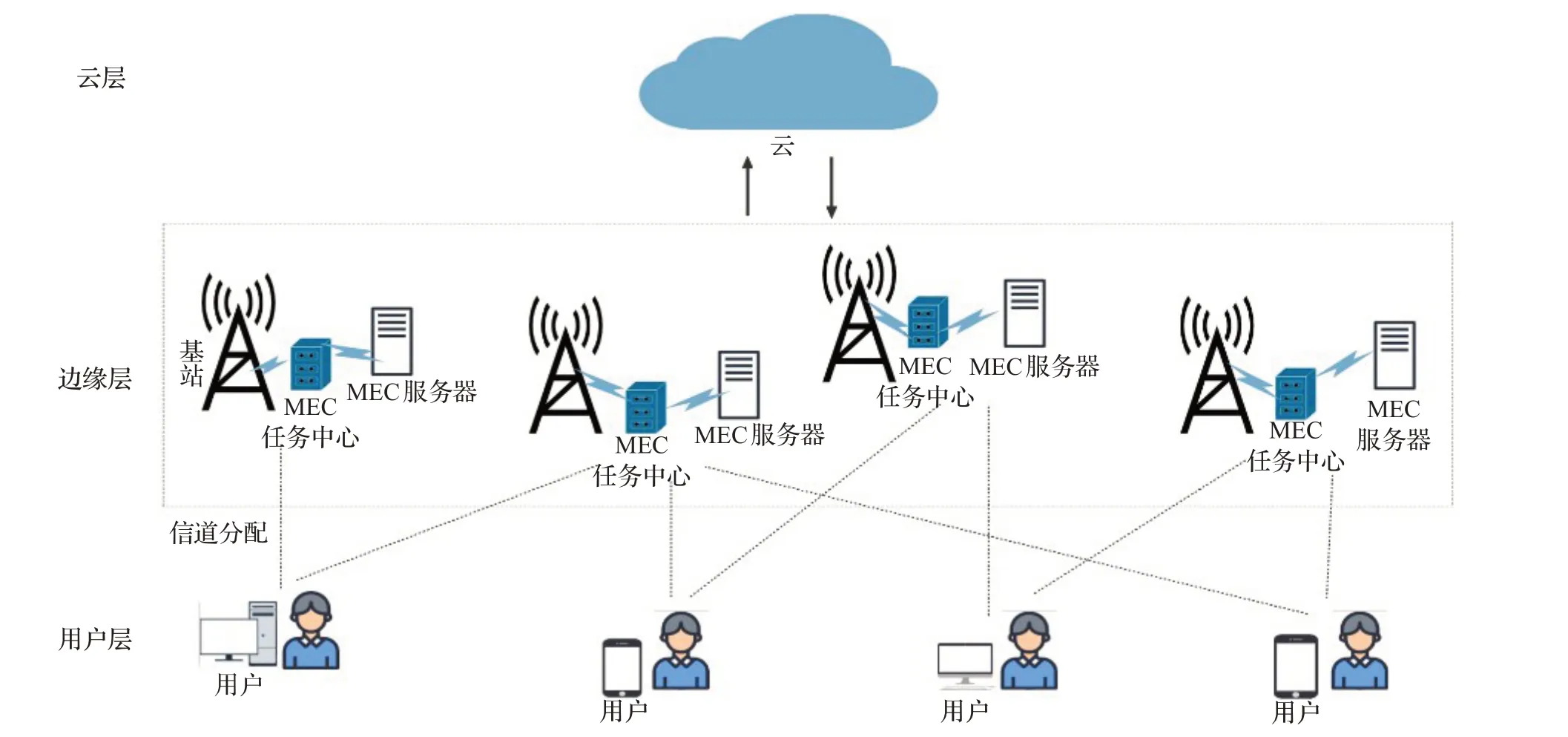
图1 移动边缘计算系统模型Fig.1 Model of mobile edge computing system

每个MEC服务器都有一个任务池JOB_POOL，用于存储UE卸载到MEC服务器的任务，按照FIFO（先入先出）原则对卸载任务进行计算。然后，每个服务器处理任务的数量是有限的，因为当大量移动设备将任务卸载到同一服务器时，该服务器的负载会很高，这些卸载的任务会经历较大的处理延迟，而具有最大可容忍延迟的任务可能会在到期时被丢弃。同样，每个用户都有一个工作池LC_POOL和一个迁移池TRANS_POOL，LC_POOL用于存储在本地执行的任务，按照FIFO原则对任务进行本地计算，而TRANS_POOL用于存储卸载到服务器的任务，按照FIFO原则对任务进行上传。

在MEC系统中，每个移动用户有多个计算密集型任务（任务在执行过程中，数据大小都保持不变），每个任务具有不可分割性和最大可容忍延迟，任务集合被表示为U={u1,u2,…,uq}，而每个任务被定义为一个三元组ui=(ci,di,γmaxi),i∈q。其中，ci表示完成任务ui所需的计算资源量（CPU周期数），di表示任务ui的数据大小，γmaxi表示任务ui的最大允许延迟（意味着任务完成时间的阈值）。任务在t时刻的状态分别有：（1）任务开始卸载（SO）；（2）任务正在上传（SU）；（3）任务正在处理（SP）；（4）任务完成返回给用户（TB）；（5）断开连接（TD）；（6）任务正在迁移（ST）；（7）任务在本地执行（TL）。移动用户有两种卸载模式[14]：分别是二进制卸载和部分卸载，本文考虑的是二进制卸载。每个任务对应一种卸载策略，表示移动用户n将任务卸载到MEC服务器m上，则表示在本地进行计算，但是同一个移动用户的任务只能卸载到同一个MEC服务器，如果MEC服务器的任务数量已经达到阈值（任务池处于满的状态），则任务迁移（按照FIFO原则）。通过上述的讨论，将包含所有任务卸载变量的卸载策略集合P定义为P={pinm|pinm=1,n∈N,m∈M,i∈q}。移动用户n上的任务卸载数至多等于q：

该系统具有三层架构：云层，通过云接受并处理用户信息来判断移动用户是否进行卸载。边缘层，由多个基站和多个MEC服务器组成。MEC服务器通过基站获取计算和存储资源，用户通过将任务卸载到MEC服务器上处理来减少能耗和降低时延。用户层，受自身计算能力和能源的限制，部分任务需要卸载到边缘层处理，以提高服务质量，例如手机、车辆和无人机。

2.2 通信模型

在OFDMA中[15]，由于通信信道的正交性，同一区域内的移动用户不能相互影响，只有位于不同区域且使用相同子信道的移动用户才能相互影响。这里假设每个移动用户均处于不同区域，它们之间不会相互影响。每个移动用户和BS之间都有一个上行通信链路，UEn和BSm之间上行链路的信道增益被定义为hnm，移动用户的功率集合被定义为P={pn|0＜pn＜P,n∈N}，P是功率的最大阈值。基于香农定理[7]，移动用户n的传输速率可以计算为：

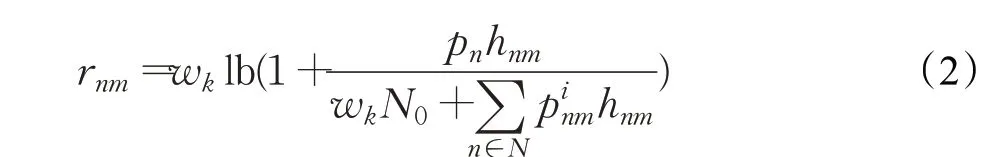
其中，wk为无线信道带宽，N0为高斯白噪声的方差。

2.3 计算模型

2.3 .1本地计算模型

将移动用户n的计算能力（每秒可执行的CPU周期数）定义为flocaln，不同移动用户的计算能力不同，如果移动用户n的任务ui选择在本地执行，则将移动用户n在本地执行任务的时延定义为Tlocaln：

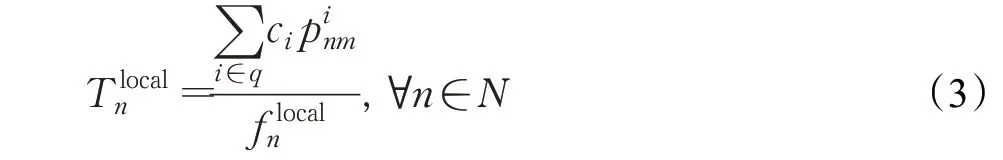
其中，ci为任务ui需要的计算资源。

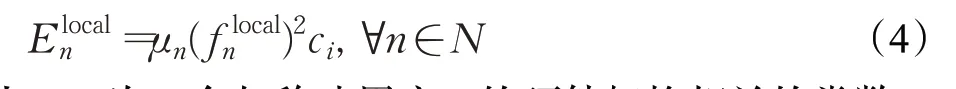
其中，un为一个与移动用户n的硬件架构相关的常数。

根据延迟公式（3）和能量消耗公式（4），移动用户n的本地计算总成本表示为：

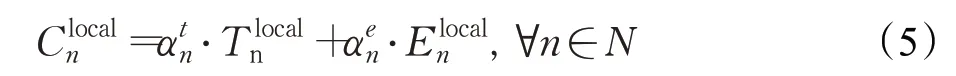
2.3 .2计算卸载模型

每个BS处的MEC服务器可以同时向多个移动用户提供计算服务，通过卸载算法判断任务是否卸载，再通过移动用户和MEC服务器之间的距离来确定目标服务器集合，然后移动用户通过分配的通信信道k将任务数据上传到MEC服务器，最后MEC服务器将计算结果返回给移动用户。

根据上述步骤可以得知上传数据的过程中会产生时延，并且不可忽略。因此，将上传数据时产生的时延定义为传输时延：

其中，rnm表示网络模型中移动用户n和MEC服务器m之间无线信道的上传速率。

移动用户n上传任务的能量消耗定义为Eupn：

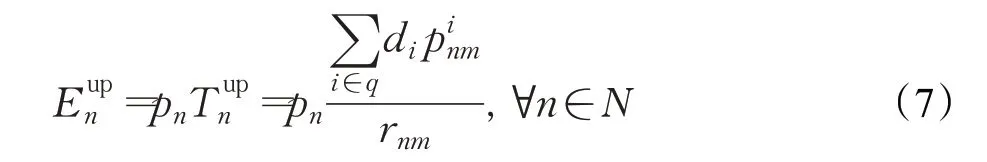
每个MEC服务器具有更强大的计算能力F和更稳定的能源供应，MEC服务器给移动用户n分配的计算资源为（每秒可执行的CPU周期数）。移动用户n在MEC服务器上的任务执行时间定义为Tedgen：

由于MEC服务器返回的结果数据量比较小（和上传的数据量相比），并且移动用户的下载速率通常很高，因此，下载部分被忽略。移动用户n卸载任务的总时延定义为Toffn：

任务卸载时，移动用户n消耗的能量仅与数据传输相关，所以移动用户n卸载任务的总能耗定义为：

结合延迟公式（9）和能量消耗公式（10），移动用户n的计算卸载总成本表示为Coffn：

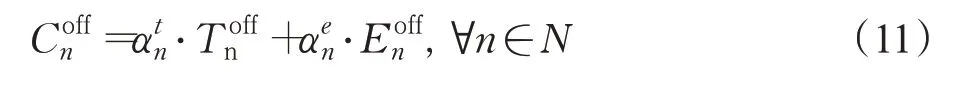
3 问题定义

对于MEC系统中的分布式卸载决策和资源分配方式，每个移动用户根据本地信息做出卸载决策，然后MEC服务器根据移动用户的信息以及卸载策略分配资源，以最小化用户总成本。本文以移动用户的传输功率、卸载决策和CPU能力为控制变量，构建了一个效用函数，该效用函数为移动用户的执行时间和能量消耗之间的权衡。在满足每个任务的最大可容忍延迟的要求下，问题S1的表述如下：

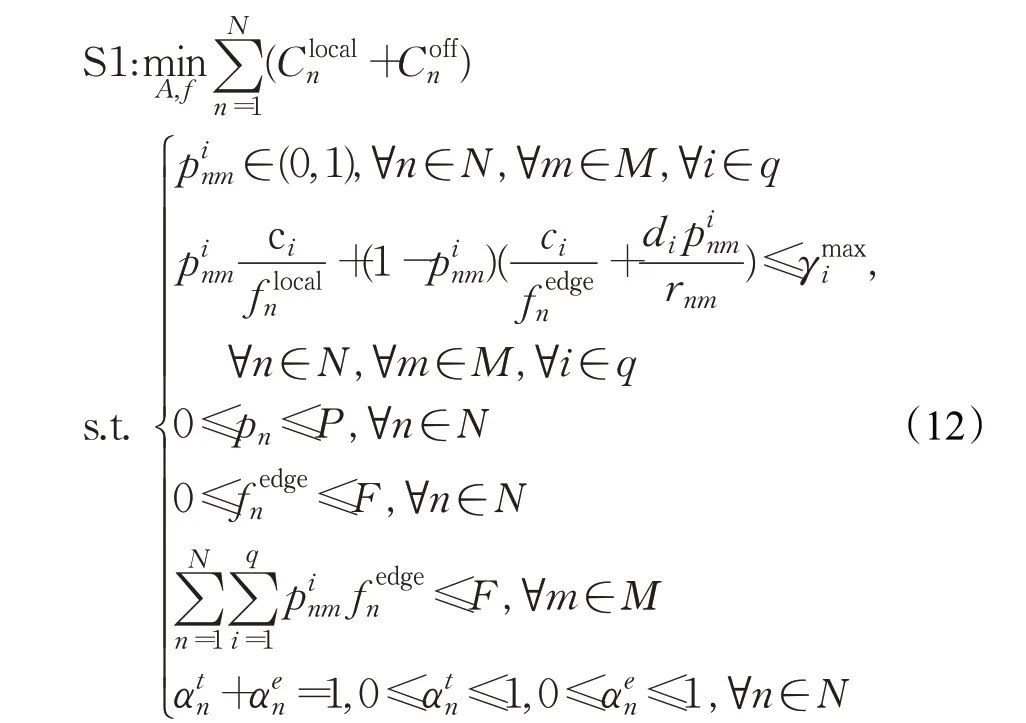
约束1任务只能卸载或者本地执行。

约束2无论是本地计算还是卸载计算，任务的完成时间都不能超过任务的最大可容忍延迟。

约束3移动用户n的功率不能超过P。

约束4在卸载计算期间分配给移动用户n的计算资源不超过MEC服务器总的计算资源。

约束5分配给移动用户总的计算资源不能超过MEC服务器总的计算资源。

约束6移动用户的时延和能耗权重之和必须等于1，并且二者的取值必须在0～1。

需要解决的主要问题是移动用户如何以分散的方式选择这些变量值，从而使移动用户成本最小化。为了使移动用户成本最小化，不同移动用户之间的卸载决策和传输功率控制都属于NP问题[9，16]。在本文中移动用户的传输功率、卸载决策和CPU能力三个变量相互关联、相互耦合，因此可以看出S1也是一个NP问题。并且，如果移动用户数量持续增加，问题S1的求解集合规模会呈指数增长。本文的优化目标是在所有可能的卸载策略中，最大化可获得的计算资源数量，同时最小化移动用户成本。ρ是MEC系统选择的一个卸载策略，是所有可行的卸载策略集合。此外，优化目标还需要满足两个资源约束：计算资源约束和通信资源约束，分别是MEC服务器分配的计算资源在任何时候都不能超过MEC服务器总的计算资源和在传输信道中分配的通信资源不得超过MEC系统提供的带宽。本文提出一种基于单代理策略的计算卸载方法A-DDPG来解决资源分配问题，与基于值的RL方法不同，A-DDPG采用了双actor-critic架构[17]，可以有效地解决连续控制问题。接下来详细地介绍提出的A-DDPG算法以及具体的结构组成。表1总结了本文中使用的一些重要符号。

表1 符号说明Table 1 Symbol description

4 A-DDPG算法

DDPG算法[18]是一个随机优化框架，由三个基本元素组成：（1）状态；（2）动作；（3）奖励。在t时刻，agent根据状态S(t)做出相应动作A(t)，然后动作A(t)再与环境进行交互返回下一个时刻状态S(t+1)和奖励R(t)，通过返回的奖励值大小判断动作是否积极，从而选择奖励值最大的动作和系统进行交互。在本文的MEC系统中，三个元素定义如下所示。

状态在时隙t，用S(t)表示系统状态：

其中，rm表示服务器m可获得的资源量；Bnm表示用户n和服务器m之间通信连接可获得的带宽；On表示用户n任务集的卸载决策；LOn表示用户n的位置坐标向量；JOB_POOL表示任务池的长度；TRANS_POOL表示迁移池的长度。

动作在时隙t，用A(t)表示卸载过程的动作，包含了给用户分配的资源fedgen和带宽wk。

奖励奖励值是对以前动作获得利益的评估。本文的优化目标是使用户的总成本最小化，而深度学习的目标是获得最大的奖励回报，奖励函数应与优化目标的倒数成正相关，因此，将奖励函数定义成与用户总成本的倒数相关的线性函数：

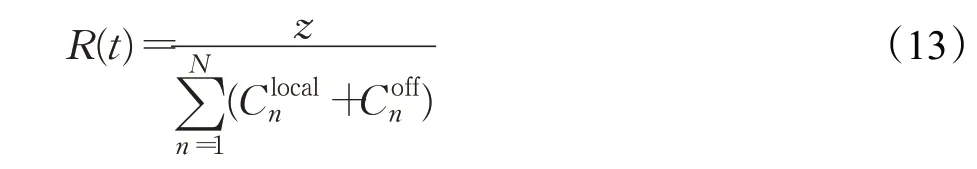
在提出的算法中，MEC服务器帮助移动用户训练模型以减轻移动用户的计算负载。每个时隙∇t中，对状态集中元素的关注度并不相同，比如：如果服务器的任务池长度已经达到阈值，则没有必要再关注服务器的可获得计算资源和带宽，以及为它们分配其他的存储空间和进行训练，而Attention机制对神经网络进行一定优化处理以及增强元素之间的局部联系，从而减少占用的存储空间和提高模型的训练速度和训练效果。首先将状态集合S(t)输入到LSTM状态编码器，再通过Attention LSTM处理得到不同状态的注意力权重值，然后输出状态的注意力权重向量，大小为[batch x n_hidden]。在A-DDPG算法中，分别有两个actor网络和critic网络，因此，A-DDPG有来自四个网络的梯度流，加上双误差反向传播，使用LSTM能更快地训练模型。

5 算法设计

本文的目标是设计一个卸载算法A-DDPG，通过在线算法获得二进制卸载决策之后，使用A-DDPG算法获取较优的资源分配，从而最小化目标函数。卸载过程由两个交替的阶段组成：卸载动作生成和资源分配更新。卸载动作生成是在所有可能的卸载决策中随机进行选择，资源分配更新则是通过A-DDPG算法实现，A-DDPG算法的结构如图2所示。该算法的实现基于DDPG[19]。由于DDPG是一种无模型的方法，它可以解决复杂的系统和移动设备之间的交互，而不需要系统和移动用户交互的先验经历，同时，该算法可以处理系统潜在的大状态空间。

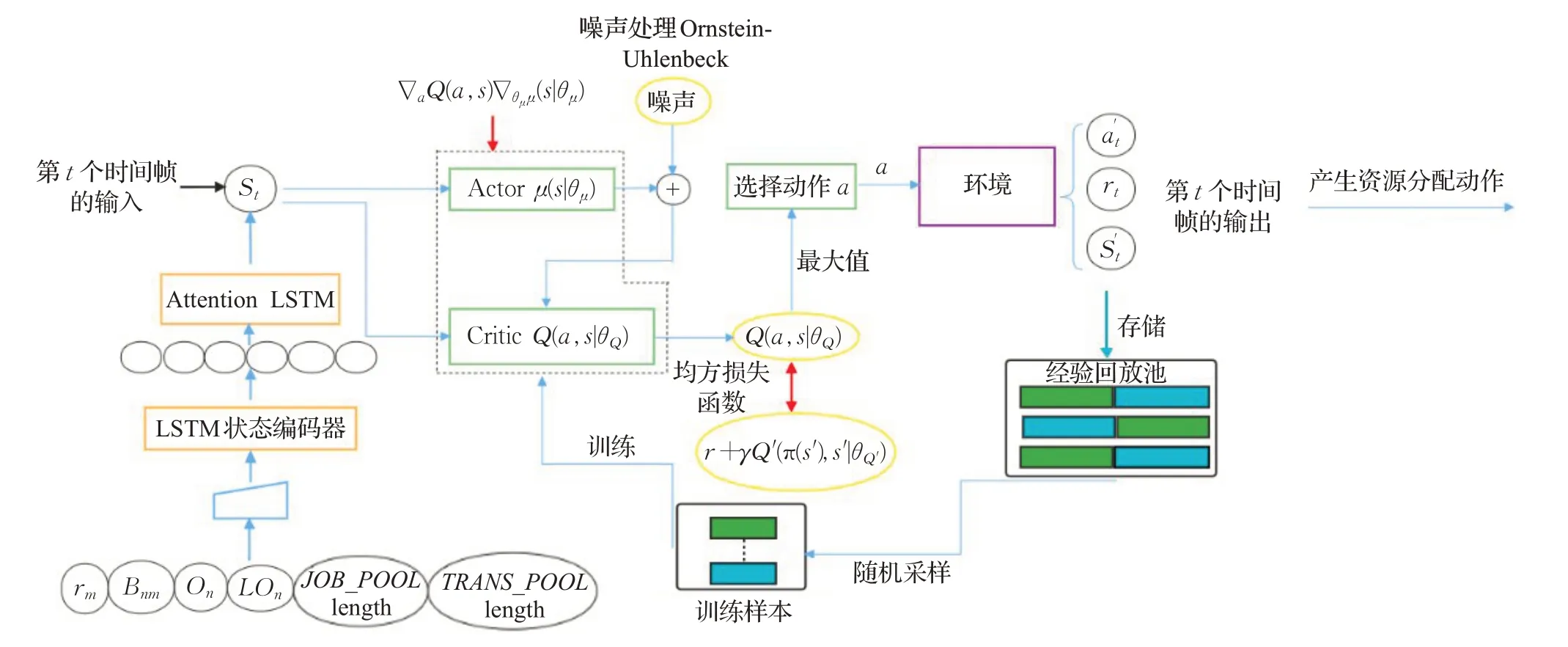
图2 A-DDPG算法结构Fig.2 Structure of A-DDPG algorithm

A-DDPG算法使用DDPG学习资源分配的策略，以及利用注意力机制的长短期记忆网络对状态向量进行编码，然后输出上层神经元个数大小的注意力向量。在该算法中，神经网络模型的目标是学习移动设备和服务器进行交互后状态-动作对到Q值的映射。基于映射，选择在目前状态下产生最小Q值的动作，从而最小化用户的总成本。

神经网络的目标是找到从每个状态到动作的一组Q值的映射。如图3展示了神经网络的结构组成。具体地说，状态信息通过输入层传递给神经网络，然后根据MEC服务器的资源和带宽通过LSTM层去估计每个任务的资源分配数量，Attention层再计算出状态集合对应的key值，最后通过全连接（Dense）层去学习从所有状态和任务资源和带宽的预测分配量到Q值的映射，然后通过输出层输出。同时，Attention机制[20]通过保留LSTM编码器对输入序列的中间输出结果，然后训练一个模型对这些输入进行选择性的学习并且在模型输出时将输出序列与之进行关联（换一个角度而言，输出序列中的每一项生成概率取决于在输入序列中选择了哪些项），从而提高从状态-动作对到Q值映射的学习效率。将θm定义为神经网络参数向量，包括从输入层到R&B层的所有连接权重和偏差。每层的细节如下：

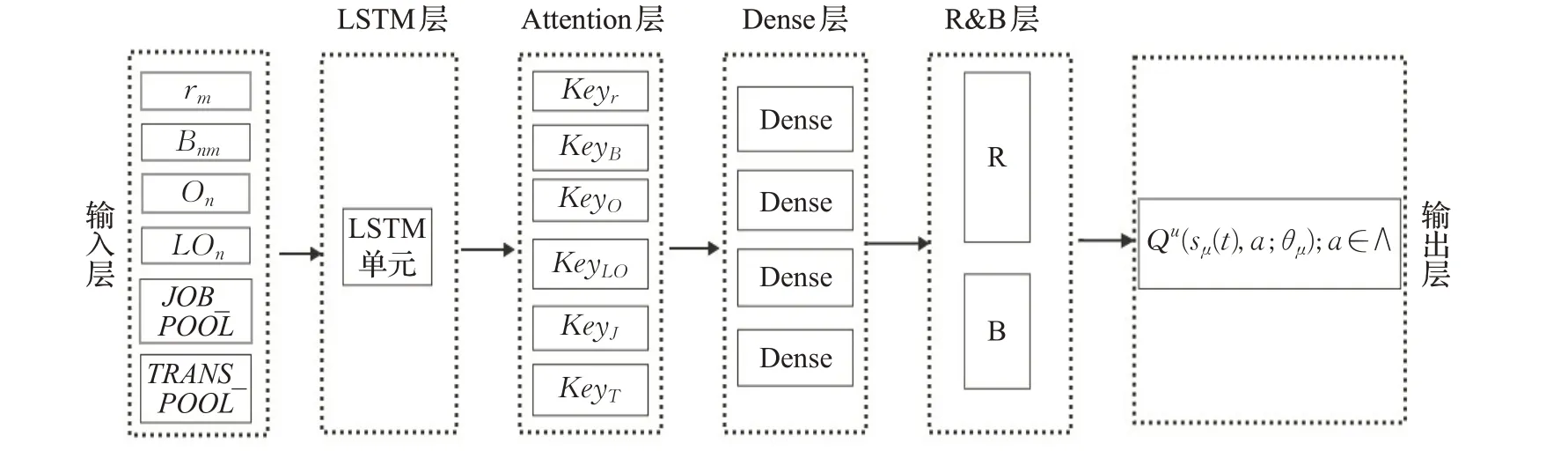
图3 神经网络组成结构Fig.3 Composition structure of neural network

5.1 Input layer

该层负责将状态集作为输入传递给下一层。在t时刻，移动用户的状态集被定义为St，其中包含每个MEC服务器可获得的资源、每个通信连接可获得的带宽、用户位置坐标等。这些信息被传入LSTM层去预测任务的资源分配量。

5.2 LSTM layer

该层负责学习MEC服务器可获得资源和带宽的情况，并预测近期任务的分配量。LSTM网络是一种被广泛用于学习序列观测的时间依赖性并预测时间序列的未来变化的方法。具体而言，LSTM网络将状态集St作为输入，学习MEC服务器可获得资源和带宽的动态变化情况。LSTM网络包含T∇LSTM单元，每个单元包含一组隐藏的神经元。S(t)输入到每个LSTM单元，S(t)的第i行表示为{S(t)}i。这些LSTM单元按顺序连接，以便跟踪从{S(t)}1到{S(t)}T∇序列的变化，这能够揭示时隙之间的MEC服务器可获得资源和带宽的动态变化。最后一个LSTM单元中输出未来可获得资源和带宽的信息，然后将输出传递给下一层学习。

5.3 Attention layer

注意力机制是从序列中学习每个元素的重要程度，然后按重要程度对元素进行加权求和，本质是一个查询（query）到一系列键值对（key-value）的映射。首先是将query和每个key（状态集中的不同元素）进行相似度计算得到状态集中不同元素的权重，然后通过softmax函数对这些权重进行归一化，最后将权重和对应的键值加权求和得到attention系数传递给下一层进行学习。

5.4 Dense layer

该层学习从状态以及可获得资源和带宽到Q值的映射。每个Dense层包含一组具有整流线性单元（ReLU）的神经元，它们与前一层和后一层的神经元相连。

5.5 R&B layer and output layer

R&B层和输出层实现DDPG算法，并确定每个状态-动作对的Q值。R&B层首先学习任务可获得的资源和每个连接可获得的带宽，然后输出层通过R&B层的学习和状态集来确定状态-动作对的Q值，其中通过评估由状态和动作产生的奖励值来改进Q值的估计。输出层包含critic网络，而R&B层由网络R和网络B构成（见图3）。网络R和网络B具有相似的网络结构，都是由输入层、LSTM层、Attention层和Dense层构成，不同的是网络R用于学习任务的资源分配情况，而网络B学习每个连接的带宽分配情况，网络R和B进行连接构建卸载网络，学习任务的卸载情况，把网络R和网络B的s、a进行叠加，通过输出层计算状态-动作对的Q值。状态-动作值函数的贝尔曼方程[21]如下（定义在状态st下，采取动作at后，且如果持续执行策略μ的情况下）：

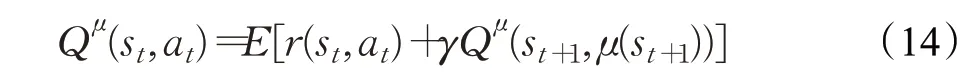
为了使长期折现收益最大化，采用时序差分法（TD），在每个时间步t更新状态动作函数：

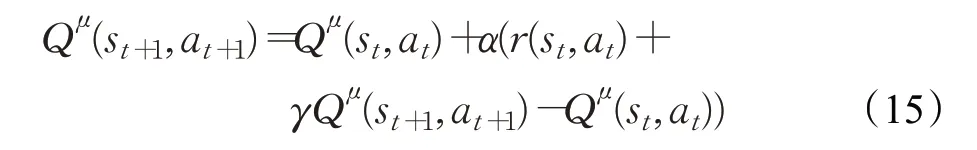
α在0到1之间，表示学习率。

R&B层作为参与者进行动作选择，输出层通过价值函数对采取策略进行评价，然后根据输出层的结果更新价值网络和策略网络。在critic网络中，利用时序差分法和最小化损失函数对参数θQ进行更新，它的损失函数[22]定义如下：

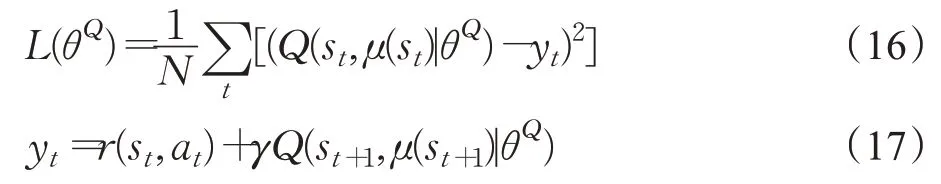
其中，yt在状态st中采取动作at后得到的最大化回报。

R&B网络最大化总体折扣奖励的期望并且用价值函数去近似整体的折扣回报，然后该网络用梯度上升法更策略以逼近最优解。

两个目标网络的参数更新均采用软更新方式[16]，其公式如下所示：

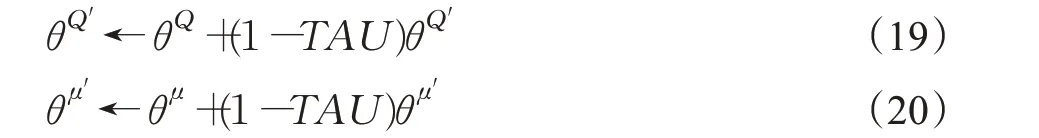
其中，TAU是软更新因子，本文将其设置为0.01。

A-DDPG算法的伪代码如下所示：

步骤1初始化critic网络θQ和R&B网络θμ。

步骤2初始化目标网络θQ′←θQ,θμ′←θμ。

步骤3初始化经验池D、探索方差r_var和b_var、学习率LR_A和LR_C、奖励折扣因子GAMMA。

步骤4对每个episode，循环执行以下步骤：

（1）获取初始化状态S0。

（2）探索step小于最大限定步数，则对它的每一步，循环执行以下步骤：

①根据当前的策略和状态st选择动作：

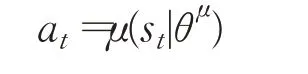
②为了进行探索，对动作添加随机噪声：

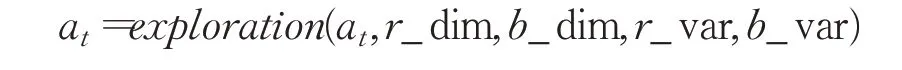
③执行动作at，得到奖励rt和新状态st+1。

④如果经验池D被占满，则用新状态集S(st,at,rt,st+1)进行替换，经验池没被占满，则直接S存入。

⑤从经验池中随机采样Z个样本进行训练。

⑥计算yt（动作的期望回报）。

⑦更新critic网络参数：

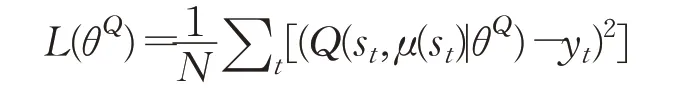
⑧每隔d步，通过确定性策略梯度更新actor网络参数θμ。

⑨每隔replace_step步，更新目标网络参数：

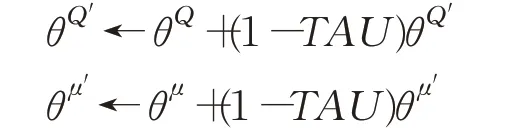
（3）结束探索循环。

步骤5结束episode循环。

6 实验结果

6.1 模拟设置

在本节中，将在不同参数设置下对提出的A-DDPG算法进行性能评估，并与其他基线算法进行比较。本文采用了韩国首尔移动用户的位置数据进行模拟（https：//crawdad.org/yonsei/lifemap/20120103/index.html）。由于本文算法没有实现真实的边缘计算环境，所以使用Python3.7.5来构建移动边缘计算网络环境，并使用Tensorflow2.2.0来实现所提出的算法。考虑的是有多个移动设备和多个边缘服务器的场景，实验中的相关参数列于表2中[18]。

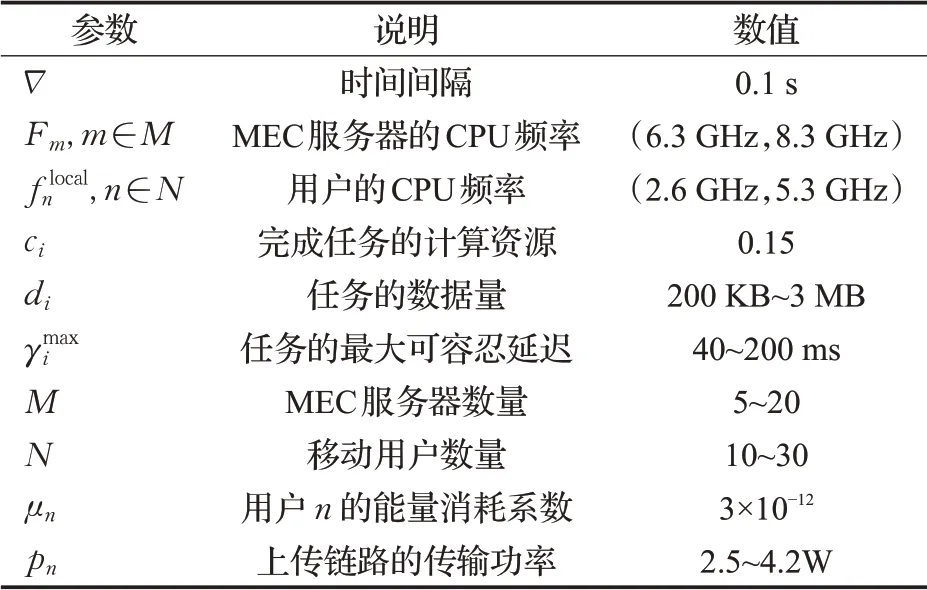
表2 参数设置Table 2 Parameters setting

神经网络的参数设置如下：batch大小通常被设置为2的幂次方，在合理范围内，一般来说batch越大，其确定的下降方向越准，引起训练震荡越小，但是增大到一定程度，其确定的下降方向已经基本不再变化，反而会导致模型收敛缓慢，泛化性差，陷入局部最优，在本文中，batch设为32时，模型性能较优；学习率的不同取值会影响模型的收敛速度，学习率取值较大会使actor网络和critic网络都采取较大的更新步长，学习率取值较低会导致DNN的更新率较慢，模型需要更多的迭代次数才能收敛，在本文中，当actor的学习率为0.001，critic的学习率为0.002时，模型的收敛性能比较好。

当奖励折扣系数设置为0.9时，经过训练的分配策略具有最佳性能，原因是不同时期的环境变化很大，所以整个时期的数据不能完全代表长期的行为。一个比较大的奖励折扣因子意味着将整个时间段内收集的数据视为长期数据，导致不同时间段内模型的泛化能力较差。因此，对奖励折扣因子设置一个适当的值将提高训练策略的最终性能；随机探索控制因子设置为1。同时，使用Adam算法进行优化。在环境模拟中，考虑的是一个平稳环境，即策略函数（在状态中执行的动作）和价值函数（从状态-动作对到Q值的映射）不会随时间变化。如果环境发生了变化，则该算法可以通过将随机探索控制因子重置为1来重新适应环境，从而继续进行随机探索。将时间间隙Δ设置为0.1，每隔一个间隙移动用户会发生一次移动。

6.2 算法比较

为了研究影响算法性能的因素，本实验改变了三个参数设置。另外，在不同的参数设置中，还有其他四种卸载方法与所提算法进行了比较。下面对这几种方法进行了描述：

（1）在本地执行所有任务（Local）：移动用户的所有计算任务都在本地执行，而不请求计算卸载到MEC服务器。

（2）基于DDPG的卸载算法（DDPG）[21]：DDPG是actor-critic算法，它在算法训练的收敛性等方面具有独特的优势。该算法最近在许多研究中被使用，这就是选择该算法作为实验比较算法的原因。

（3）基于TD3的卸载算法（TD3）：TD3算法对DDPG算法的一些不足之处进行了一定优化，采用双网络结构解决过估计问题，在探索中增加随机噪声提高actor网络的寻找速度，并且A-DDPG算法是在TD3的基础上提出。

（4）基于DDPG的卸载算法（Noisy-DDPG）：在DDPG算法的基础上添加了噪声层的卸载算法，增加了网络的随机探索率。

在实验中，如果移动用户数、MEC服务器数和权重不作为参数对照，则分别默认为10，10，αtn=0.8,αen=0.2

在深度强化学习中，神经网络需要进行训练得到合适的Q值，以更好地适应环境给出的奖励和策略。A-DDPG算法分别有两个神经网络来拟合策略和Q值。如图4是神经网络的训练过程。可以看出，在训练开始时，由于动作是随机选择的，再加上探索噪声，因此主体正处于探索阶段，奖励值较低。随着迭代次数的增加，主体从探索阶段慢慢进入使用经验的学习阶段，算法快速收敛，奖励值逐渐趋于稳定。从图4中可以看出A-DDPG算法的收敛速度比较快，在episode=10时，A-DDPG算法已经趋于稳定，而且奖励值远远高于其余几个算法。

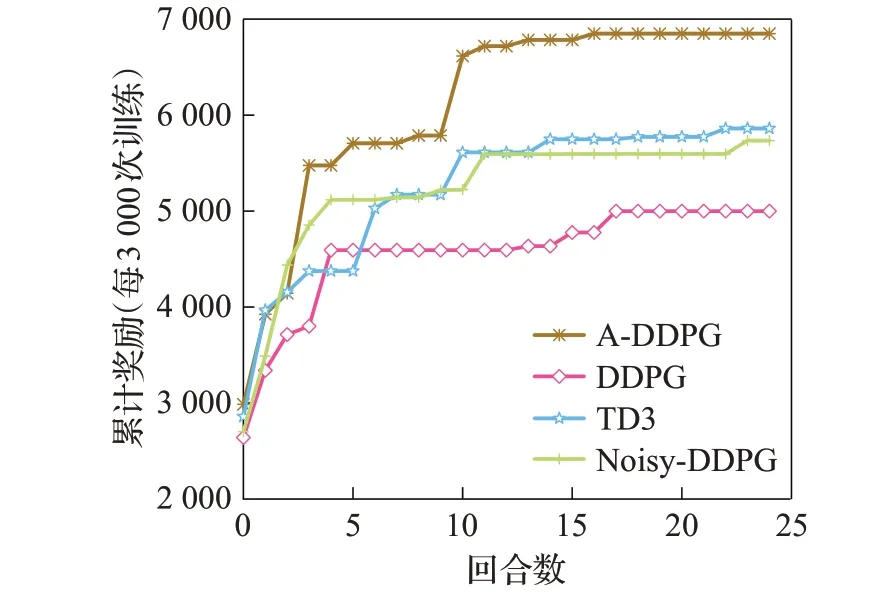
图4 总奖励价值迭代训练Fig.4 Iterative training of total reward value

如图5显示了用户总成本随训练次数增加的趋势变化。总的来说，随着训练次数的不断增加，四种方法的总成本逐渐下降。本文提出的A-DDPG算法取得了最好的结果，当算法均趋于稳定时，A-DDPG算法的用户总成本最小，比DDPG算法低27%左右。

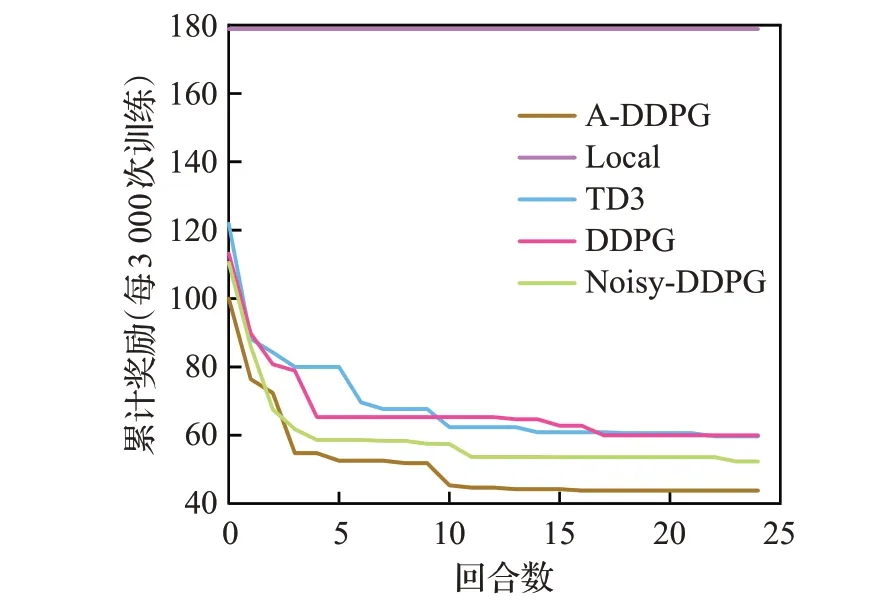
图5 总成本迭代训练Fig.5 Iterative training of total cost

为了验证所提算法的有效性，比较了不同用户数和设备数下的用户总成本。在图6（a）中，可以看到，随着UE数的增加，用户的总成本呈现出整体上升的趋势，但当用户数越多时增长越快。这是因为当用户数量变大时，MEC服务器的计算资源不足以提供给所有移动用户。容量有限的MEC服务器不能服务太多用户，所以在这种情况下选择一个合适的卸载决策是非常重要的。在图6（a）中，可以看出A-DDPG算法是优于其他几种算法的。当用户数等于30时，A-DDPG算法的总成本和TD3算法的相差不大，但是A-DDPG算法在用户数等于10和20的情况下，总成本都比较低。总的来说，随着移动用户数增加，A-DDPG算法的性能高于其他几种算法。

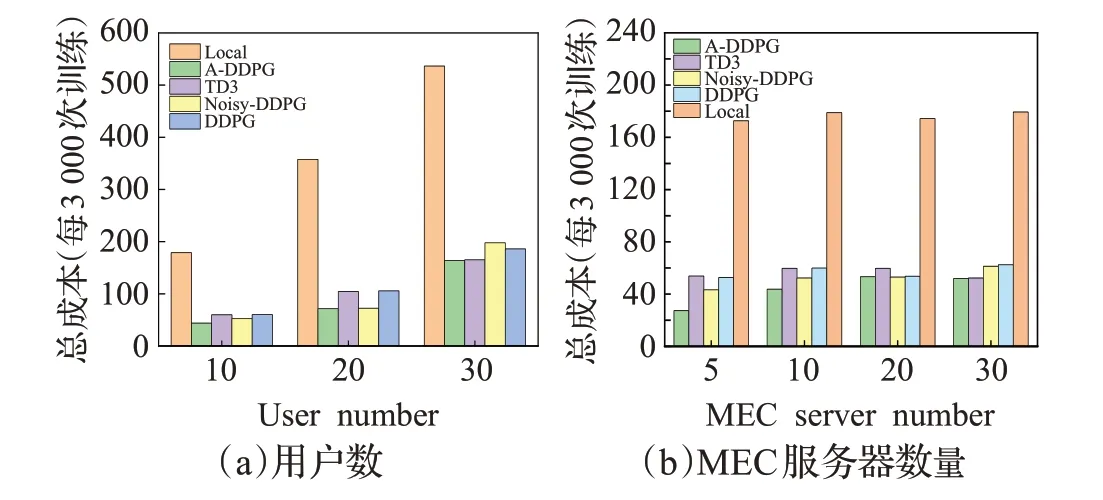
图6用户数与MEC服务器数对比Fig.6 Comparision of user number and MEC server number

图6 （b）显示了当MEC服务器数量持续增加时，Local算法、DDPG算法、Noisy-DDPG算法、TD3算法和A-DDPG算法的性能比较。当边缘服务器数量从5台增加到20台时，只有Local算法的总成本没有太大的波动，而其他几种算法都是先增后减的趋势。可以看出增加服务器数量并不会显著提高效果，用户的总成本主要是受到网络带宽和用户自身CPU容量的限制，但是，可以看到A-DDPG算法的性能仍然是优于其他几种算法。

在本文中，同时考虑了延迟和能耗，并且设置了不同的权重参数满足各种类型应用的需求。从图7可以看到，在不同的权重参数设置下，提出的方案仍然是有效的，可以实现更低的用户总成本。

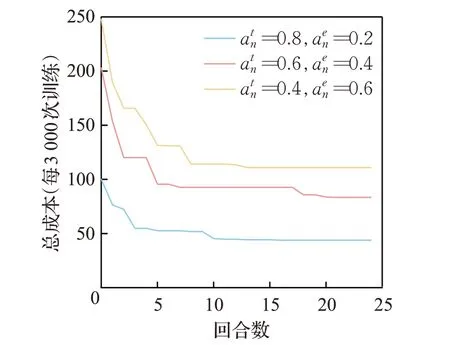
图7 权重占比Fig.7 Weight ratio

在本文中，每个任务都具有最大可容忍延迟。任务完成时间超过自身的最大可容忍延迟，则认为任务失败。通过比较训练过程中任务平均失败率来验证A-DDPG算法的性能。在图8中，MEC服务器数设置为5。可以看出几种算法的任务平均失败率都呈现下降趋势，但是A-DDPG算法在episode=5时已经收敛并且任务失败率为0，而TD3算法在episode=10时才收敛，DDPG算法在episode=14时任务平均失败率才为0，所以A-DDPG算法优于TD3算 法、DDPG算法和Noisy-DDPG算法。

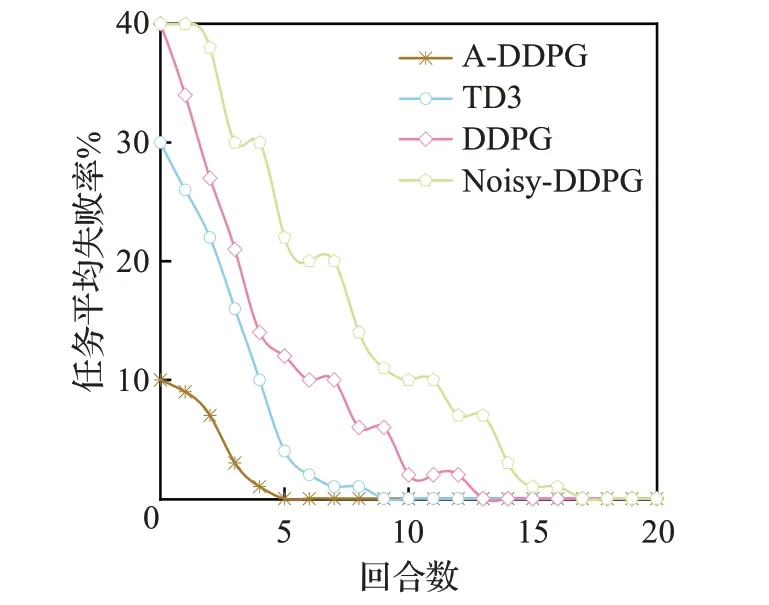
图8 任务平均失败率Fig.8 Average failure rate of tasks

7 结语

在本文中，讨论了多用户多MEC服务器环境下移动设备的计算任务卸载策略以及用户的移动性问题，还考虑了服务延迟、能耗和任务失败率等衡量指标，并且针对不同的应用类型，对延迟和能耗设置了不同的权重值，解决因用户类型不同带来的不公平问题。为了最大限度地降低用户的总成本，本文提出一种改进DDPG的计算卸载算法（A-DDPG），解决了DDPG算法和TD3算法处理计算卸载时的不稳定性和收敛速度慢的问题，同时优化了DDPG内部网络的权重参数更新过程。在现实场景中，MEC服务器资源是有限的，如何提高资源利用率是一个关键问题。此外，对于更大规模的边缘计算系统，提高服务器计算能力和网络带宽对于服务质量的保证至关重要。提出了A-DDPG卸载算法解决上述提出的问题，并利用真实的移动数据集进行了多次实验，实验结果表明，在多用户多MEC服务器系统中，本文算法优于其他算法。不足之处在于，用户的任务都具有不可分割性，以及任务的卸载决策是确定的，本文期望这种基于DDPG的卸载算法（A-DDPG）能进一步改进，以在未来的MEC网络中实现任务的可分割以及卸载决策的实时性。