大学生创新意识与能力培养的探索实践——以几何概型一题多解为例

刘 杰, 胡太忠, 严继高

(1.中国科学技术大学 管理学院统计与金融系, 合肥 230026； 2.苏州大学 数学科学学院,江苏 苏州 215006)

1 引 言

创新思维能力是知识经济时代下个体面对竞争挑战的必备核心能力, 大学生创新思维能力培养是实施科教兴国和建设创新型国家的必然要求.创新思维能力要求大学生敢于突破常规思维界限来思考问题, 以超常规甚至反常规的方法提出新观点或新方法, 产生新颖独到和有社会意义的思维成果.创新思维和创新能力培养不仅有利于大学生提高学习效果和丰富知识体系, 还可为工作就业奠定坚实基础, 增强大学生社会竞争力和拓宽职业发展通道[1].我国《高等教育法》明确规定：高等教育的任务是培养具有“创新精神和实践能力”的高级专门人才；麻省理工学院阿诺教授发现：曾经接受过独创性训练的人要比未接受训练的人有更多推展富有价值的革新的机会[2].探索如何培养大学生创新思维具有重要意义, 文献[2]提出大学生创新思维培养的路径包括：思维训练提升大脑活跃度、掌握创新技法拓宽思维、寻找刺激线索切入、思维模型及谋略智慧的应用创新等.文献[3]基于新时代大学生创新思维能力培养存在的主要问题, 提出课堂教学革新中应注重培养学生发散思维、直觉思维和形象思维、逆向思维、类比思维和灵感思维等.文献[1]和[4]提出具体可采用头脑风暴法、组合技法、列举法、设问法等.

在数理类课程的教学过程中,文献[5]提出温故知新、类比迁移法、总结思考和一题多解等均有助于培养学生创新能力.文献[6]以条件极值为例, 提出应当基于启发诱导、问题探究结合的研究式方式重构教学设计来培养学生创新思维意识.本文重点关注一题多解的教学方法, 强调引导学生结合相关知识方法, 采用多种思路完成同一问题的求解.该方法通过巩固学生核心知识和拓展技能, 形成知识点之间乃至不同课程内容之间的交叉融合, 进而有助于学生开阔思维广度、激发学习兴趣, 达到培养创新意识和能力的目标[7].

概率论与数理统计课程关注随机现象, 因此相较于其他数理类课程更加抽象.概率反映随机试验中事件发生的可能性大小, 学习概率对人们认识自然与社会中随机现象发挥重要作用, 高校自主招生选拔非常重视对几何概型等概率知识能力的考察.几何概率作为古典概型的拓展, 能够有效刻画随机试验的样本空间为不可数情形下的随机事件概率, 为此所采用的差异测度等特征, 对学生的概率理解和计算容易带来误解和挑战, 例如经典的贝特朗奇论问题.几何概型的概率计算方法比较灵活, 通常可以转化为几何方法进行计算, 也可借助连续随机变量及其分布密度来计算, 还可尝试利用离散的古典概型来逼近连续的几何概型.如何充分利用这种灵活性解题, 在教学过程中进行启发思考和对比分析, 达到提高学生创新意识与能力的目标, 是值得我们思考的问题.本文将以一道代表性几何概型题目的一题多解为切入, 从多种角度启发学思考思考, 激发和培养其创新意识与创新能力.此外, 通过问卷调查分析实际教学中学生课后反馈情况, 进一步验证了一题多解对几何概型教学效果提升和学生创新意识培养的显著作用.

2 一道典型几何概型题目的多角度分析

(某高校2022年度自主招生类选拔考试)在一个圆周上独立随机地选取n个点, 求所选出的n个点恰好落在一个半圆周上的概率.

图1 几何概型例题示意图

多角度思考与分析由题设可知此题属几何概型的概率求解, 不失一般性可以假设n个点互不相同.为计算所有点都能落在一个半圆周上的概率, 需要找出能够覆盖所有点最短圆弧, 确定此时圆弧的起点和终点, 才能找出对应几何概型的概率条件, 实现概率求解计算.可以考虑从多个角度入手,(i)分别计算每个点作为圆弧起点时的概率, 再求n个事件并的概率；(ii)在圆周上选定一个参照点, 将圆弧的两个端点位置表示成两个随机变量, 则问题可转化为求变量极差小于半圆弧长的概率；(iii)随机选取点的个数n具有一般性, 可尝试发掘n取不同值时的递归或迭代关系,然后由递归式求解概率；(iv)将圆周进行任意2k>n等分,n个点选自不同的等分小圆弧上,求所有点都落入同一半圆内的概率.为便于计算和表示, 记随机选取的n个点分别为B1,B2,…,Bn，用Pn表示B1,B2,…,Bn落在一个半圆周里面的概率.

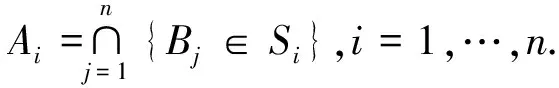
角度之二：密度积分法为不失一般性,此处假设圆的半径为1.在圆周上任意固定一个点B0，记B′0为圆周上B0的对径点.按顺时针方向记B0与Bk围成的圆弧长为Xk，则X1,...,Xn独立同分布于均匀分布U(0,2π);类似地,按顺时针方向记B′0与Bk围成的圆弧长为Yk，则Y1,...,Yn独立同分布于均匀分布U(0,2π).设Pn表示B1,B2,...,Bn落在一个半圆周里面的概率,则“B1,B2,...,Bn落在一个半圆周里”的事件可以分解为以下两种情况:

(i)X(n)-X(1)≤π.在此情况下有三种子情形可以发生:所有点落在B0B′0弧上(按顺时针方向);所有点落在B′0B0弧上;部分点落在B0B′0弧上,部分点落在B′0B0上.此情形下事件对应的概率为

(ii)Y(n)-Y(1)≤π，且去掉Y(n)≤π和Y(1)>π两种子情形.同上可求得此情况下事件对应的概率为

故Pn=P1n+P2n=n/2n-1.

图2 解法3示意图

接下来讨论第n个点的投放位置, 尝试建立Pn与前n-1个点落于半圆周内概率Pn-1的迭代关系.记C′,D′分别为C,D两点的对径点(即将C,D两点分别与圆心连接并延长交圆周), 如果要保证新投放的第n个点与前面的(n-1)个点都落在半圆周之内, 则当且仅当该点落在劣弧C′,D′以外,注意到C′,D′形成的劣弧张角为Θn-1，故

Pn=Pn-1×P(B1,…,Bn在半圆周内|B1,…,Bn-1在半圆周内)

=Pn-1×P(Bn落在对应劣弧C'D'|B1,…,Bn-1在半圆周内)

利用初始条件P2=1(即：圆周上随机任选2个点一定在某半圆内), 可得Pn=n/2n-1.

角度之四：离散逼近法首先考虑将几何概型进行离散化, 对于n≥3情形,将圆周进行2k等分,其中k>n；将分出的2k个区域依次编号为1,…,2k，2k个区域对应2k个空位, 并在2k个空位中随机独立地放置n个点, 故共有(2k)n种放法,即样本空间大小|Ω|=(2k)n.尝试借助古典概型计算n个点随机落在k个相邻空位的概率, 然后令k趋于无穷,逼近题设中的几何概型的概率.

图3 解法4示意图

“n个点落在相邻的k个空位”等价于“间距最远的两个点(按照顺时针方向不妨设为B1和B2)所落的位置编号间隔小于k”, 为求出所有的放置方法的种数, 接下来分情况进行讨论.

(i)假设B1和B2所在区域编号相差为0(即为同一区域), 则B1有2kn种可能取法(从n个点中选有n种可能,从2k个区域选择一个有2k种选取方法)；B2从余下的n-1个点中选取放在同一区域, 有n-1种可能, 余下的n-2个点放置位置唯一.故在此种情况下, 总放置方法为2kn(n-1)种.

(ii)假设B1和B2所在区域编号相差为1(即相邻), 则B1的放置方法有2kn种；B2的放置方法有n-1种, 放置的区域是唯一的；余下的n-2个点放置方法有2n-2种.故在此种情况下, 总的放置方法为2kn(n-1)2n-2种.

(iii)依此类推, 假设B1和B2所在区域编号相差为j，其中2

综合以上所有k+1类情况的结果,n个点随机落在k个相邻区域的放置方法种数为

|Ωk|=2kn(n-1)(1+2n-2+…+kn-2).

因此根据古典概型,n个点随机落在k个相邻区域的概率为

易见k→∞时,n个点随机落在k个相邻区域的概率逼近n个点随机落在一个半圆周上的概率, 即

所以, 题目所求n个点随机落在一个半圆周上的概率为n/2n-1.

该几何概型概率题的四种方法思路各异, 通过不同的角度进行思考与分析, 可以将问题转化成多种典型方法来求解.方法一基于加法定理, 以n个点中任意一点为基准, 围绕关键点“其余点均在该点的顺时针方向的半圆周上”, 进行事件分解并互斥性算得最终结果.方法二是利用密度函数计算概率, 在圆周上任意一点为基准, 根据其余点与该点的距离构造随机变量, 将问题转换为极差变量小于半圆周的长度.这两种解法不仅可得到半圆周时的结论, 还可拓展至求解“n个点落在任一张角为θ0的圆周上”的概率问题, 该概率值为n(θ0/2π)n-1，其中θ0∈(0,π](感兴趣的读者可以尝试计算).方法三为构造递归关系式, 先假设前n-1个点B1,…,Bn-1已落在一个半圆周, 再考虑新投放第n个点来建立Pn与Pn-1的迭代式.方法四更体现灵活性和创造性, 将圆周离散等分网格化处理, 利用古典概型和大数律求得结果.综上, 该几何概型问题的多种解法可有效帮助学生将概率论中的多个知识点(如随机变量、次序统计量、分布函数、概率密度函数、期望等)建立联系, 加深学生对概率知识框架体系的理解, 启发创新意识.

3 教学效果分析

经过多学期平行课堂的教学实践, 概率论与梳理统计的一题多解教学方法对激发培养大学生创新意识与能力非常有效.对相关问题进行问卷调查和统计分析, 问卷涉及了5个问题, 分别调查学生对几何概型知识点的理解掌握、多知识点的联系建立、启发多角度思考、创新思维培养、学习效果提升的看法.采集到有效问卷115份, 数据分析结果如图4所示.

图4 问卷调查结果统计图

问卷调查结果显示, 超过80%的学生认为一题多解对以上教学效果指标的提升程度比较显著, 其中约40%学生认为非常显著, 数据充分证实“一题多解”在几何概型教学中的重要作用; 进一步分析各指标间的相关性, 发现相关性系数大致为0.8, 说明通过一题多解能够有效建立多角度思路、多知识点联系、创新思维形成等方面的相互促进机制.

4 结 论

本文通过某自主招生测试概率题的一题多解，结合多种知识点从不同角度进行思考与分析，意在激发与培养大学生创新意识与能力.教学实践与问卷调研分析表明：一题多解一方面推动了课堂教学的多元化和灵活性、激发学习兴趣, 显著加强了学生灵活掌握多个知识点的纵横联系、提高了核心知识点的学习效果、锻炼了学生分析解决问题的思维灵活性; 另一重要方面是激发和培养创新意识与能力, 这对数理类课程激发与培养创新意识与能力有一定的借鉴作用.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.