基于小波变换的层序识别分析与研究

◇中国石油辽河油田分公司勘探开发研究院 董足华

高精度的层序识别对于油田勘探开发具有十分重要的作用，常规的层序识别方法存在一定的缺陷，尺度较大，精度较低。本文主要对基于小波变换的层序识别方法进行了分析与研究，首先简要阐述了小波变换的基本理论，然后对小波变换层序识别的理论基础和关键步骤进行了详细分析，其次结合模型试验验证了该方法的有效性，以期为高精度层序识别提供一种有效手段。

层序地层学的相关理论和分析方法对油田的勘探开发具有非常重要的指导作用。层序地层学（sequence stratigraphy）是在地震地层学基础上发展以来的一种地学理论，主要研究地下年代地层格架中岩石关系、具有成因联系的地层或岩相分布模式，其基本单位是层序[2]。对于层序地层学而言，其中最核心、最重要的问题就是层序识别，主要包括2个方面：①层序界面的识别；②层序的划分。近些年以来，人们越来越重视高精度层序识别技术的发展和应用，一般情况下研究人员都是利用露头、钻井岩心、古生物资料、测井以及地震等数据进行层序的识别，但是常常缺乏露头、钻井岩心、古生物资料，而地震数据的信噪比和分辨率也比较有限，因此最常使用的资料就是测井数据[1-2]。

目前，基于测井数据的层序识别方法比较多，如砂泥比曲线法、时（深）-频分析法、声波时差法、最大熵谱分析法、曲线活度分析法等[1-3]，但是这些方法仅仅适用于大的层序界面的识别，很难适用于目前油田精细挖潜的需求。经过多年的研究和发展，研究人员开始尝试使用各种信号分析的方法（短时傅里叶变换、小波变换、Hilbert-Huang变换、经验模态分解、变分模态分解等）来提高层序识别的精度，以此建立更加精细的层序地层格架。本文主要对小波变换的层序识别进行分析与研究，以期为测井数据层序识别提供一种科学、有效的方法。

1 小波变换

为了突破和改进传统的信号分析方法的缺陷，如傅氏变换、STFT变换、Wigner变换、Gabor变换等，19世纪70年代以Morlet为首的法国工程师提出了小波变换，该变换被誉为“数学显微镜”。小波变换是一种新的时频分析方法，该方法能够提供一个“时间-频率”变化的信号分析窗口，不但具有多尺度分解的能力，而且还具有局部分析能力，除了分析常规的平稳信号，还可以分析非平稳信号，尤其是可以突出信号某些方面的特征，有效解决了传统信号分析方法不能解决的很多难题[2-4]。

小波变换的基本原理如下：

从上述公式可知，小波变换的本质是将一维的时间序列变成一个二维参数空间（、），进而可以在时间、空间来分析信号特征。

2 小波变换层序识别理论基础

沉积旋回是各个不同时间沉积事件的周期性叠加结果[4]。目前为止，在研究人员获得的所有资料中，测井数据是连续性最佳而且分辨率最高的一种资料。测井数据正好可以记录一段时间中各个沉积事件，可以反映出地层的各种沉积特征，如周期性、连续性、旋回性等。但是测井数据反映的沉积特征本质上是不同频率与幅度沉积事件的叠加，存在各种因素引起的随机干扰，使得具有区域可比性的沉积特征就隐藏在这些随机干扰中，如果采用人工判读的方式，则很难识别这些隐藏的沉积特征，具有比较大的主观随意性。小波变换可以对测井数据进行多尺度分解，将其分解成不同尺度的沉积旋回，进而暴露出其中的沉积特征，利用这些特征就可以对地层层序进行识别和分析。

3 小波变换层序识别关键步骤

3.1 测井曲线的优选

测井曲线的优选是小波变换层序识别的关键环节，对是否可以准确识别地层层序的岩性突变界面具有直接影响。对于岩性剖面，虽然各种测井曲线得到的小波变换结果在形态和幅度上存在一定的差异，但是对沉积旋回界面的响应基本相同。大量学者的理论研究和事件证实，自然伽玛曲线（GR）对地层中泥质含量的变化反映比较敏感，可以较好地反映地层的各种沉积特征，如旋回性、周期性、连续性等。因此，GR曲线是小波变换层序识别常用的理想曲线[3-4]。

3.2 小波函数的选择

一般而言，小波函数不具有唯一性，对相同的信号选择不同的小波函数所得到的分析结果相差比较大，因此，对于小波变换层序识别而言，小波函数的选取同样具有十分重要的意义[5]。小波变换是利用小波函数与待分析的信号进行相关运算进而得到不同尺度的系数，系数越大说明该信号与小波函数的波形相似程度越高，计算之后的能量就比较集中，能够大幅提高计算效率。研究人员通常选择二进制dbn系列小波，通过相应的实验分析发现，如果n值过大或过小都会影响地层层序界面的分辨率，过小则能量不集中，减小高频信息的分辨能力，过大则会造成低频边界模糊[4-5]。

3.3 尺度因子的确定

测井曲线是由很多不同周期的地层沉积旋回叠加而成，利用小波变换可以分解成不同独立周期的沉积旋回，并且以不同尺度的形式呈现出来，因此，尺度因子的确定十分重要。如果尺度因子越大，说明小波函数被伸展，空间观察的窗口越大，则对应测井曲线的长周期分量，说明地层的沉积时间长，旋回的厚度大，可用来识别大级别的旋回；如果尺度因子越小，说明地层的沉积时间短，旋回的厚度小，可用来识别中期、短期、超短期等小级别的旋回。

4 模型测试

为了说明小波变换在层序识别中的有效性，本文构造了相应的地质模型，该模型由4个大级别的正旋回构成，而每个正旋回中又存在3个小级别的正旋回，每个小级别的正旋回中有3种岩性，从上到下依次为泥岩、细砂岩、粗砂岩，如图1所示。通过试验对比分析，本文选用了db2小波函数，尺度因子为8，通过小波变换对地质模型中2个级别的正旋回进行了刻画。从图1中可知，1阶高频信息中11个较大异常值的位置正好对应了模型中12个小级别旋回的界面，再结合7阶低频信息，从而可以准确划分出模型中12个小级别正旋回；同理，利用1阶高频信息和7阶低信息可以准确识别4个大级别正旋回。

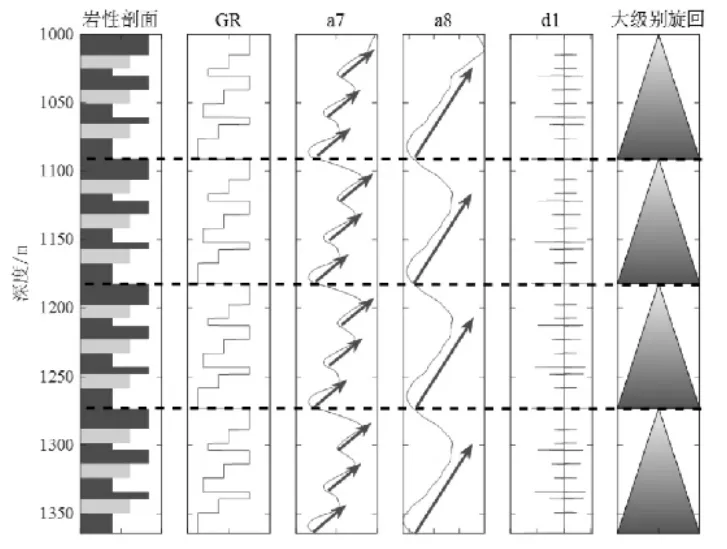
图1 基于小波变换的层序识别效果

5 结论与认识

（1）小波变换具有比较好的时频分析能力，具有直观性、可靠性的优点，利用多尺度分解之后的GR曲线能够反映岩性变化特征，进而可以识别地层中大、小级别的旋回，减少了人为因素的影响，为高精度层序识别提供了有效的工具。

（2）在实际层序识别过程中，研究人员不能仅仅使用基于测井曲线的小波变换技术，而应该根据工区的地质特征以及所收集的资料情况，优选合适的层序识别方法，如地震相位法、地球化学法、神经网络法等，综合考虑层序识别方法的优点，采用组合识别的方式，在一定程度上可以大幅降低单一方法的多解性，从而提高层序识别的精度和可靠性。