基于SEIQR模型在高校疫情传播仿真模拟

◇贵州大学数学与统计学院 王丙硕 贺孝英 张梨 朱文涓 胡尧

本文为验证高校隔离措施的有效性，运用SEIQR模型模拟了校内COVID-19疫情在不同的隔离措施下传播的情况。通过对比分析，得到增设隔离点能有效降低感染峰值，缩短疫情持续时间的结论。鉴于此，合理规划校内隔离设施的投入有利于校园疫情防控。

新冠肺炎疫情发生以来，中国疫情已得到明显控制，但全球疫情形势仍不乐观，疫情防控具有长期、复杂及不确定的特点。当前，全球疫情仍在快速蔓延，多个国家新增确诊人数出现暴发式增长，疫情输入风险有所上升，国内疫情也有反复现象。接种疫苗是防控疫情的有效手段之一，截至2021年10月25日，全国接种新冠疫苗224621.7万剂次，但仍需坚持疫情防控措施，不能放松警惕。

对COVID-19发展趋势和传播模型的研究，对抑制疫情的传播具有重要的意义。结合新冠病毒自身特性，针对COVID-19传播规律和预测分析，较多学者基于SIR模型和SEIR模型开展研究。针对SIR模型，张艳霞[1]等用改进的SIR模型和龙格库塔法模拟计算，预测新冠疫情传播规律，得出降低日接触率可有效防控的结论；尹楠[2]通过构建SIR模型对有限区域新冠肺炎疫情的扩散进行模拟仿真，并提出相应对策建议；朱仁杰[3]等以SIR模型为基础，考虑感染系数随时间的变化，利用回归分析进行参数估计，模拟预测了多个国家疫情发展趋势；任中贵[4]基于SIR模型分析武汉疫情数据，讨论模型中两个参数的拟合结果，说明了封城等措施及提高医疗能力的重要性；黄梅[5]通过改进SIR模型，引入政府管控力度等作为参数，基于卫健委公布的数据进行参数估计及预测分析，说明了政府管控力度对疫情传播的影响。针对SEIR模型，赵子鸣[6]等利用周期性边界的SEIR空间传播模型分析，对社区防控提出指导建议；冯苗胜[7]等结合SEIR与logistic模型，达到很好的预测效果；喻文[8]通过改进SEIR模型仿真模拟，为高校重点区域风险管控提供建议。在当前学者的研究方法中，多数设定模型未考虑隔离人群或仅在建议中提及隔离措施，少有文献展现隔离对疫情的实际影响程度。

鉴于此，本文针对高校内新冠疫情传播情况，考虑隔离因素，基于经典传染病模型构建SEIQR模型，揭示实行隔离措施前后新冠病毒在高校内的传播规律，为校园疫情防控提供理论依据。

1 SEIQR模型

1.1 符号的定义

本文构建SEIQR模型[9]，将人群划分为五类：其中S指易感人群，未得病，但与感染者接触后容易转化为I类人群；E指处于潜伏期的人群，已感染但未表现出感染症状；I指感染人群，已感染并表现出症状；Q指隔离人群，感染并表现出症状后被收治隔离；R指移除人群（治愈或死亡），不再对病毒传播产生影响。分别表示时刻的易感人群总数、潜伏期人群总数、感染人群总数、隔离人群总数和移除人群总数，而表示防控区域内总人数，N为不变量。

1.2 基本假设

（1）在观察区域范围内，将总人数N划分为易感、潜伏、感染、隔离、移除五类人群。

（2）潜伏期患者具有传染性，可感染易感人群。

（3）潜伏期患者平均每日接触易感者人数高于感染者。

（5）隔离人群治愈率略高于感染人群。

（6）新冠肺炎治愈者获得免疫力后不会二次感染。

1.3 模型建立

（1）建立SEIQR模型示意图。

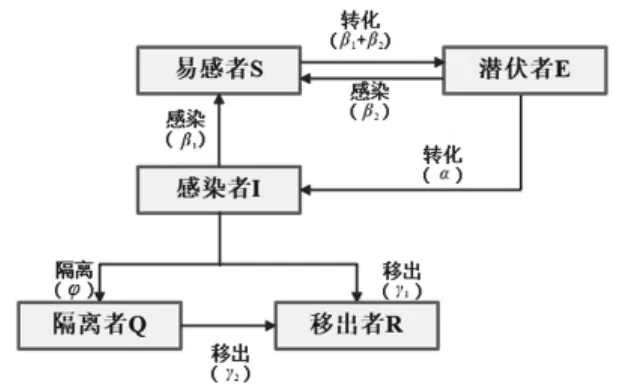
图1 SEIQR模型人群状态转化图

（2）建立状态方程。

a、t时刻内易感人群S可被潜伏人群E和感染人群I感染，利用得易感人群S的控制方程为：

b、t时刻内潜伏人群E与感染人群I均可感染易感人群S使其变为潜伏人群E，而潜伏人群E又有一定概率转化为感染人群I，利用和得潜伏人群E的控制方程为：

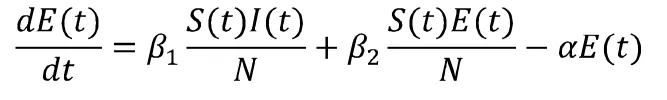
c、t时刻内感染人群I一方面因潜伏人群E的转化而增加，另一方面因一定概率移除和隔离而减少，利用得感染人数I的控制方程为：

2 Monte Carlo 模拟仿真研究

2.1 参数赋值

2.2 未增加隔离措施，即取隔离参数 =0

设教学楼单次容纳量为3000人，初始感染者为1人，无潜伏患者存在，模拟针对感染者的无隔离措施时，教学楼130天内新冠病毒的传播情况，得出易感者、潜伏着、感染者、移出者的数量随时间的变化关系。从图2中可以看出，感染曲线在32日左右达到峰值，最高感染人数为868人，即最大感染率为29%，疫情持续时间146天。

图2 =0时SEIQR模型仿真结果（教学楼）

2.3 高校实施隔离措施

（1）高校高度重视感染者的隔离情况。设置校内隔离点，建立健全完备的隔离流程，校内感染者一经发现能被及时收治隔离。

（2）加强对校内人员健康状况的监管力度，如强制校内师生填写体温信息收集表，及时发现体温异常者并采取必要措施。

（3）鼓励学生积极配合学校安排，如按时并正确填写自身体温情况，不瞒报自身身体状况，晚间按时打卡确保在校内，减低感染风险。

2.4 采取隔离措施后

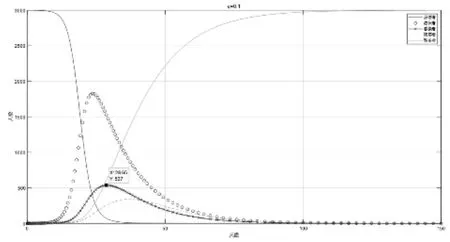
图3 =0.1时SEIQR模型仿真结果（教学楼）

由图3可以看出，感染者人数于29日左右出现拐点，其峰值为537人。相比无隔离措施，峰值降低331人，疫情持续时间缩短21天，防控效果显著。

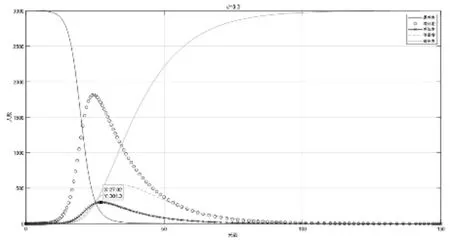
图4 =0.3时SEIQR模型仿真结果（教学楼）

图4结果显示，感染者人数于27日左右出现拐点，其峰值为302人，疫情持续112天。相比无隔离措施，峰值降低566人，拐点提前5天。

图5结果显示，感染者人数于26日左右出现拐点，最高感染率不超7%。相比，拐点出现时间并无明显变化。

图5 =0.5时SEIQR模型仿真结果（教学楼）

由图6可得，疫情于27日后出现拐点，感染者峰值为158人。相比无隔离措施时的最高感染率29%，时，感染率下降约23.6%。

图6 =0.7时SEIQR模型仿真结果（教学楼）

图7数据显示，疫情于27日后出现拐点，感染者峰值为128人。感染率下降24.7%。疫情于100天后结束，相比无隔离措施时，缩短46天。

图7 =0.9时SEIQR模型仿真结果（教学楼）

2.5 结果分析

（1）教学楼区域疫情传播情况。

表1 不同值下教学楼区域疫情传播情况

表1 不同值下教学楼区域疫情传播情况

b、感染峰值随参数变化为：

图8 感染峰值随变化趋势

曲线严格单调递减，即随着隔离参数的增大，感染人数峰值不断降低；或者说，当值从0.9不断减小时，感染者峰值呈几何式增加，表明隔离措施对疫情防控具有显著影响。

（2）针对其他模拟区域—宿舍、食堂。

仿照上述步骤，保持其他参数不变，调整N的取值，分别模拟宿舍、食堂区域内疫情传播情况。针对宿舍、食堂区域，分别取N值为1300、600，得到如下表格。

表2 不同值下宿舍、食堂区域疫情传播情况

表2 不同值下宿舍、食堂区域疫情传播情况

3 总结

3.1 结论

3.2 意义

随着各高校陆续复学，校园疫情防控将面临“实战”考验。各地高校的疫情防控与全国疫情防控密切相关，重要性不言而喻。本文针对高校疫情传播进行仿真模拟，演化高校疫情传播过程。对比和分析实行隔离措施前后新冠病毒传播的差异，说明高校疫情防控常态化的重要性。为切实做好校园疫情防控工作，各高校必须高度重视卫生教育，提高防控意识，以确保教学工作正常进行。