KPCA-GPR模型在常压塔塔顶汽油干点预测中的应用

郭丽莹，郎宪明

（辽宁石油化工大学信息与控制工程学院，辽宁 抚顺 113001）

常减压蒸馏过程是一个复杂的物理和化学变化过程，由于产品数目众多，很多变量之间耦合严重，造成常减压装置控制困难[1-3]。国内多数炼油厂都没有安装质量分析仪表，只能间隔几个小时对常压塔侧线产品进行抽样离线化验分析，根本无法实现对产品质量的实时监控。常压塔塔顶干点直接影响产品的质量、产量以及能源消耗量，采用软测量方法对筛选的常压塔塔顶干点实现在线估计，可实现对筛选干点的推断控制[4-5]。

由于软测量技术针对过程控制可实现更为严格的卡边优化控制，近些年对软测量方法的大量研究成果不断涌现。多变量统计建模逐渐发展成更具有代表性的方法[6]，支持向量机（SVM）[7]与人工神经网络（ANN）[8]这些方法通过训练对主导变量具有一定的预测能力和较好的泛化能力。但是，由于常减压蒸馏过程随着原油生产方案的变化常常显示动态特性，这些建模方法往往在预测精确度上达不到要求。高斯过程回归（Gaussian Process Regression，GPR）作为一种非参数概率，根据实际工况建立基于相似准则的局部模型，不仅可以给出干点预测值，还可以得到预测值对模型的信任值[9-11]。因此,可以使用GPR软测量模型对常压塔塔顶汽油干点进行预测。

常减压蒸馏过程是一项比较复杂的工艺流程，变量之间的复杂关联导致所采集的变量数据过多，但是对过程控制有用的信息却很少。因此，基于数据驱动的软测量方法在建模前一定要对数据进行预处理[12-13]。目前解决信息冗余的主要算法有主成分分析法(Principal Component Analysis,PCA)[14]、偏最小二乘法(Partial least squares,PLS)[15]。近年来，很多学者都致力于二种方法的改进，在数据预处理中得到了广泛的应用，由于变量数据间存在严重的耦合性和非线性，因此核主元算法（KPCA）应用较为广泛[16-18]。本文利用KPCA对过程变量进行分析，对过程变量进行降维，解决了不同变量之间的非线性相关性，然后采用GPR建立软测量模型，进而建立了KPCA-GPR常压塔塔顶汽油干点模型。

1 KPCA-GPR建模算法

1.1 KPCA算法原理

设数据样本集为X={x1,x2,…,xk,…,xn}，其中xk∈Rn,n为样本总数；Φ为一个非线性映射，对应的空间为F,F中的样本记为Φ(xk)，且满足：

且F空间中样本的协方差矩阵为：

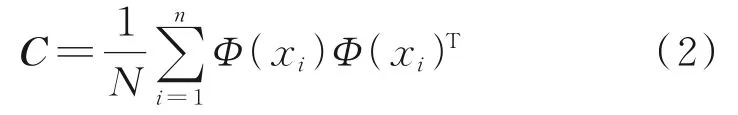
式中，N=n-1。

C的特征 值λ和特征 向量V满 足：

其中，特征向量V可由投影到F空间内的样本映射组成。

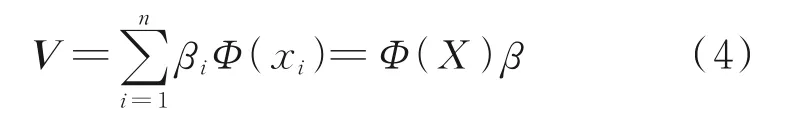
式中，Φ(X)=[Φ(x1),Φ(x2),…,Φ(xn)]；β=[β1,β2,…,βn]T。由此，式（4）可改写为：

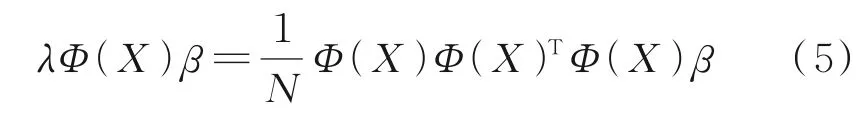
等式（5）两端左乘Φ(X)T，即：

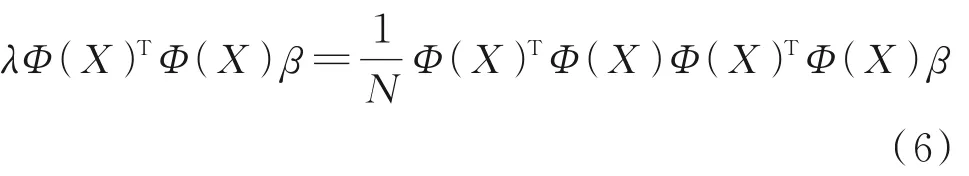
引入核函数Ki,j：

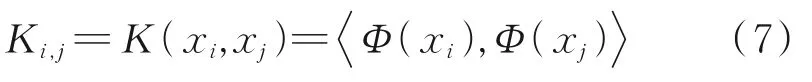
式中，i、j=1,2,…,n。

式（7）用与核矩阵K的特征值λ和特征向量β表示。

即：

对核矩阵进行中心化处理，结果如式（10）所示。

式中，In为所有元素均为的n维矩阵。

本文采用的径向基函数为：

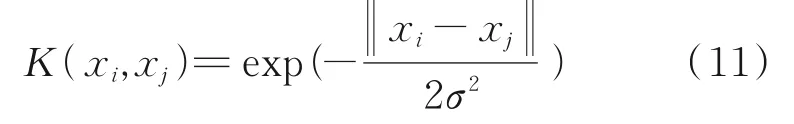
式中，σ为方差，σ＞0；‖xi-xj‖为欧氏距离。

1.2 GPR模型

GPR模型是近几年发展起来的一种机器学习回归方法，并取得了许多研究成果，现已成为研究热点，在许多领域得到了成功应用[9-11]。

GPR模型是有限个数的任意随机变量均具有联合高斯分布的集合，其性质完全由均值函数m(x)和协方差函数c(x,x')确定。均值函数m(x)和协方差函数c(x,x')的表达式为：

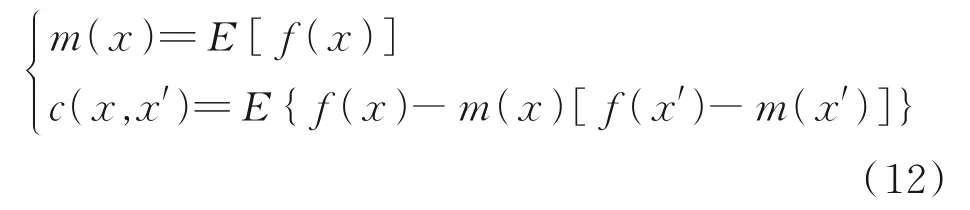
式中，x、x'∈Rd为任意随机变量，因此GPR模型可定义为f(x)⊂GPR[m(x),c(x,x')]，通常对数据作预处理，使其均值函数等于0。回归问题模型可表示为：

式中，ε为微小误差；y为受噪声影响的观测值。进一步假设噪声ε～N(0,δ2n)，可得观测值y的先验分布为y～N[0,c(x,x)+δ2n In]以及观测值y和预测值f*的联合先验分布：

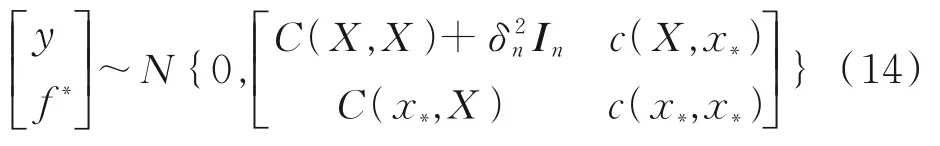
式中，X为训练集的输入；x*为测试样本集的输入；C(X,X)=Cn=(cij)为n×n阶对称正定协方差矩阵；C(X,x*)=C(x*,X)T为x*与X之间的n×1阶协方差矩阵；c(x*,x*)为x*自身的协方差。由此可以计算预测值f*的均值和方差。

2 软测量建模

2.1 常减压蒸馏工艺流程分析

常减压蒸馏过程是将不同化学成分物质分离的过程，从蒸馏的结构上看，它是一个典型的、复杂的多侧线系统。常减压蒸馏装置用于对原油的一次加工，将原油根据现实要求分为不同的馏分。常压塔不同馏分的产品成分与这段时间内进料温度、压力，塔内各处温度、压力，回流量等过程变量密切相关，一旦过程变量的变化明显，则会对产品质量造成影响。在实际生产过程中，通过抽取大量的数据样本在一定时间间隔内进行离线化验分析，获得干点、凝固点、闪点等产品指标，其滞后性大，难以实现实时的自动控制，使整个常减压蒸馏过程的产品质量。常减压蒸馏工艺流程如图1所示。图中，M为自控泵。

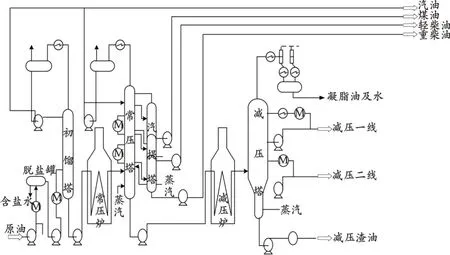
图1 常减压蒸馏工艺流程

采用软测量建模，从采集到的样本中选择具有代表性的、能够覆盖正常运行工况的适当数据作为学习样本训练，只要输入实时采集的过程参数，模型就会给出相应的质量指标，从而实现产品质量指标在线测量的目标。

2.2 辅助变量的选择

辅助变量的选择应遵循常减压蒸馏过程的机理及规律[14]。通过对抚顺石化公司石油二厂操作规程的了解，结合现场生产数据，初步选择影响常压塔塔顶干点的14个辅助变量（见表1）。

表1 影响常压塔塔顶干点的辅助变量

2.3 KPCA-GPR软测量建模方法

基于数据驱动的软测量建模方法是经过数值计算而实现的。一个模型的准确性和有效性依赖于输入数据中包含的有用信息量。因此，对输入数据的预处理也是软测量建模前必不可少的一道工序。在常减压蒸馏过程中，影响常压塔塔顶干点的不同变量之间相互关联，直接建模会增加问题分析的复杂性。对模型的输入进行简化，对输入数据进行核主成分分析，可为常压塔塔顶干点建立模型奠定一定的基础。

干点影响变量为：

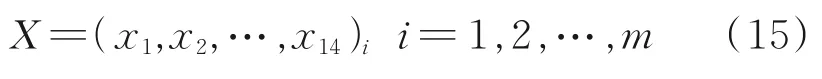
经过KPCA处理后的输入变量为：

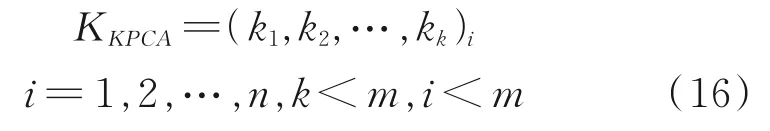
汽油干点输出变量为：

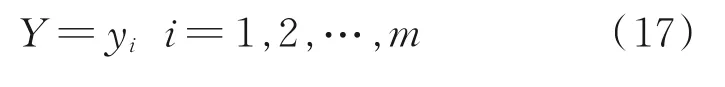
3 仿真实验

为了验证上述KPCA-GPR模型的有效性，使用某炼油厂的实际数据进行系统仿真分析。从现场采集的数据虽然拥有大量的原始信息，但是由于所得数据易受到测量方法、人为操作因素、环境因素等因素干扰，需要在进行数据预处理之前做好筛选、误差处理等工作。

3.1 基于KPCA算法的数据预处理

将经过处理的数据分成训练集和测试集。根据交叉验证法选择模型参数，经过多次实验，最终将其中300组数据用于训练，100组数据用于测试。在使用KPCA提取数据信息时，贡献率ak表示每个主成分包含原始总信息量的多少。累计贡献率bk表示前k个主成分对原始信息提取的能力。一般情况下，当bk≥85%时，就可以用k个主成分来表示原有指标而不会损失过多信息。贡献率ak和累计贡献率bk表示为：

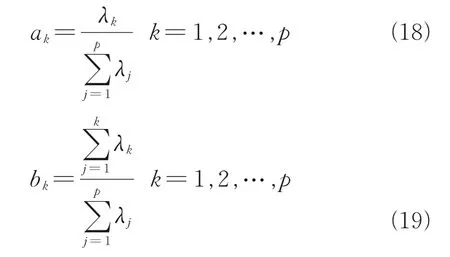
采用MATLAB软件进行仿真实验，分别使用PCA、KPCA算法计算贡献率和累计贡献率，计算结果如表2所示。表2中，R1-R6表示前6个主元。

表2 基于PCA、KPCA算法的贡献率和累积贡献率

3.2 GPR建模

基于离线数据训练得到汽油干点软测量模型，将原始数据经过PCA、KPCA处理后作为输入变量，汽油干点化验值作为输出变量，代入GPR模型中进行学习，保证汽油干点模型能实时准确预测出当前时刻干点值的均值和方差。为了更好地对比，采用均方根误差（RMSE）和平均绝对误差（MAE）作为模型性能评价准则。

分别使用GPR、PCA-GPR、KPCA-GPR建立常压塔塔顶汽油干点软测量预测模型，常压塔塔顶干点预测均值可视化结果如图2所示。GPR、PCAGPR、KPCA-GPR模型性能如表3所示。

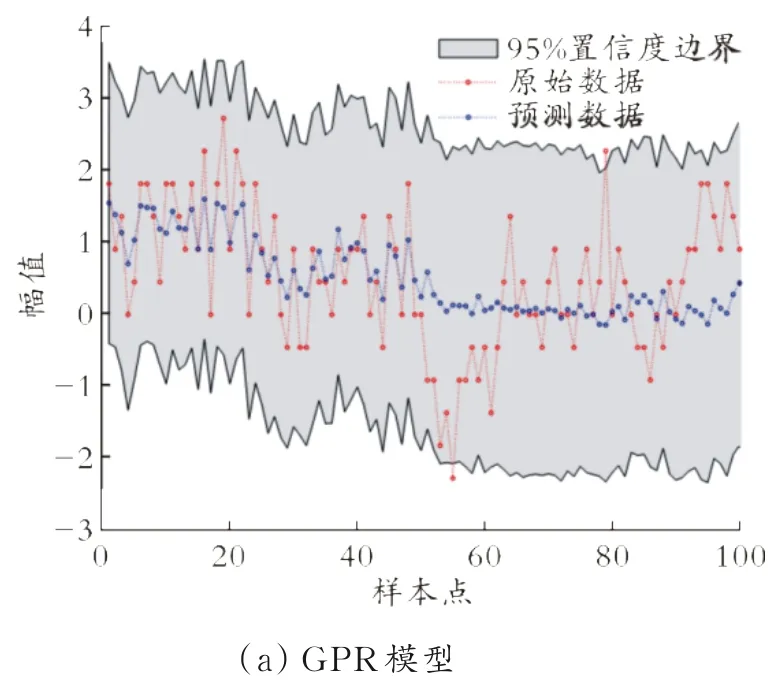
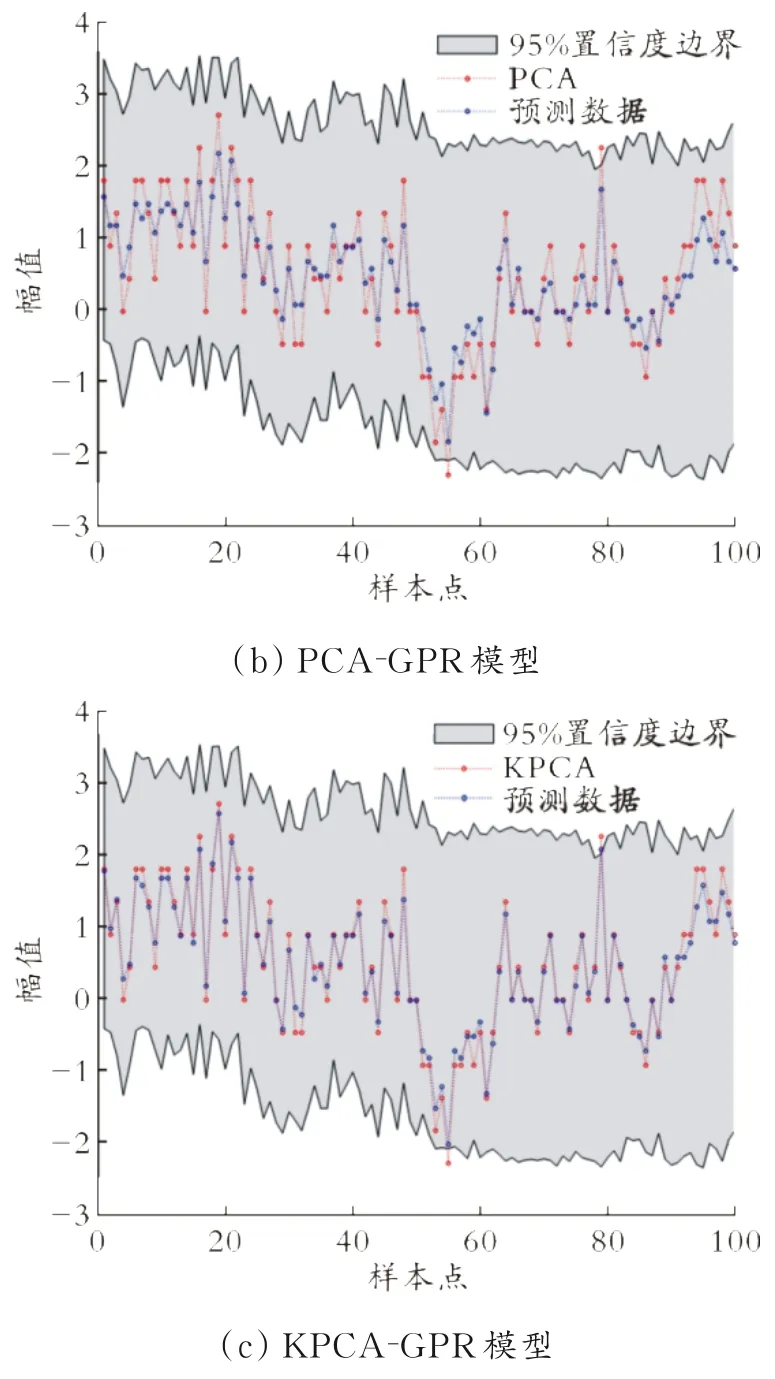
图2 常压塔塔顶干点预测均值可视化结果

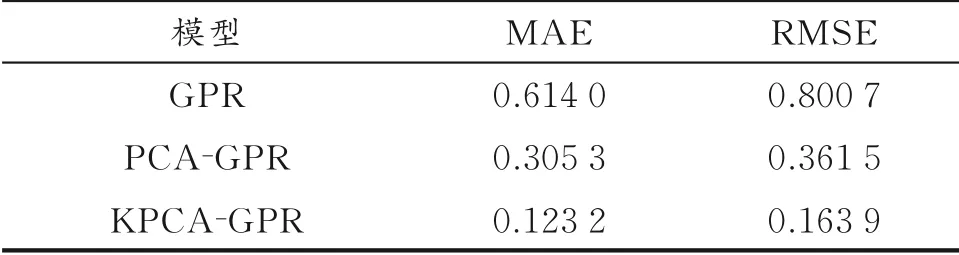
表3 GPR、PCA-GPR、KPCA-GPR模型性能

从图2可以看出，KPCA-GPR与GPR、PCAGPR相比，预测精度有所提高，基本上能满足工艺的要求。对比表3的数据可知，KPCA-GPR模型性能优于GPR、PCA-GPR模型。因此，KPCA-GPR模型具有更好的预测精度和应用前景。

4 结论

针对常压塔塔顶干点预测提出了KPCA-GPR软测量方法。首先，对数据样本采用核主成分分析进行预处理，解决变量间的非线性问题，降低数据的维数，减少噪声的干扰，提高主成分的稳定性；用未经预处理数据和经过PCA和KPCA处理的数据进行了分析。结果表明，KPCA-GPR模型有较高的预测精度和较好的模型性能。