精准设计题目 提升课堂效率
——以数列分奇偶项求和的高三复习课为例
2023-01-11福建省厦门双十中学漳州校区
⦿福建省厦门双十中学漳州校区
陈 悦
1 引言
数列分奇偶项求和是一个比较难的问题,学生往往不能根据数列通项公式的特点,选择合适的求和方法来解决问题.高三的复习课是比较紧凑的,带有明确的目标.本节课主要探讨数列分奇偶项求和的四种类型:(1)相隔一项成等差数列(或成等比数列);(2)通项公式中含有(-1)n;(3)数列的通项公式以分段数列给出;(4)数列中连续两项和的问题.
复习课与习题课是两种截然不同的的课型,复习课主要是以讲解习题为载体,巩固知识和方法,并发展能力,与新授课不同[1].教学设计主要包括了以下五个环节:回顾知识要点、分析例题、反馈练习、巩固提高以及归纳总结.
2 确定教学目标
第一,通过知识回顾、例题讲解、反馈训练、巩固提高等一系列教学活动,让学生能够基本掌握常见的数列分奇偶项求和的方法.例如,分组求和法和并项求和法.第二,数列分奇偶项的求和问题也会和其他求和方法相结合,要引导学生根据不同的题目条件,选择最优解决问题的方法.第三,要引导学生进行数学表达,由特殊到一般,要善于归纳总结,不仅要能想出来、说出来,还要能准确规范地用数学语言表达出来.第四,促进学生思维的发散,比如相隔一项成等差数列可以转化为分奇偶项求和的问题,那么如果是相隔两项成等差数列呢?当然,最主要的是在教学各个环节渗透化归与转化以及分类讨论等数学思想方法,培养学生的探究精神以及分析解决问题的能力,提升学生的数学抽象、数学运算、逻辑推理等核心素养.
3 教学实施过程
第一环节:知识回顾.

设计意图:复习本节课要用到的知识,以及数列分奇偶的常见类型.
第二环节:例题讲解.
例1(2004年北京理第14题)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.已知数列{an}是等和数列,且a1=2,公和为5,那么a18的值为;这个数列的前n项和Sn的计算公式为.
思路分析:根据数列的定义,可以得到an+an+1=5,把a1=2代入,容易发现,奇数项的值都为2,偶数项的值都为3,所以a18=3.第二空要求数列的前n项和,需要对n进行分类讨论.
师:好,那数列{an}的通项公式要如何表达?
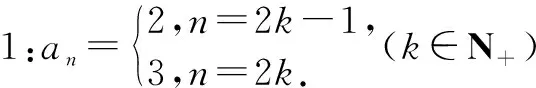
当n为奇数时,
Sn=a1+a2+……+an-1+an
=(a1+a3+……+an)+(a2+a4+……+an-1)
当n为偶数时,
Sn=a1+a2+……+an-1+an
=(a1+a3+……+an-1)+(a2+a4+……+an)

例2(2022年漳州市二质检第8题)已知Sn是数列{an}的前n项和,a1=1,a2=2,a3=3,记bn=an+an+1+an+2,且bn+1-bn=2,求S31.
解析:由bn+1-bn=2,得an+3-an=2.发现数列{an}相隔两项依次构成等差数列.
当n=3k-2时,an=a3k-2=1+2×(k-1)=2k-1,k∈N+;
当n=3k-1时,an=a3k-1=2+2×(k-1)=2k,k∈N+;
当n=3k时,an=a3k=3+2×(k-1)=2k+1,k∈N+.
所以,数列{an}的通项公式:
这时候就可以求S31.
设计意图:例1是相隔一项成等差数列的问题,例2迁移到相隔两项成等差数列,培养学生的应用意识和发散思维.
例3已知数列{an}的前n项和Sn满足Sn=2n+1-2(n∈N+).
(1)求数列{an}的通项公式;
(2)已知bn=(-1)nlog2a2n+1,求数列{bn}的前n项和Tn.
思路分析:第(1)问比较容易,可以利用an=Sn-Sn-1(n≥2),解得an=2n.第(2)问,把an=2n代入得到bn=(-1)n(2n+1),再对数列求和.
师:同学们,接下来,怎么处理?
生2:分组求和.对n进行分类讨论.
当n为奇数时,
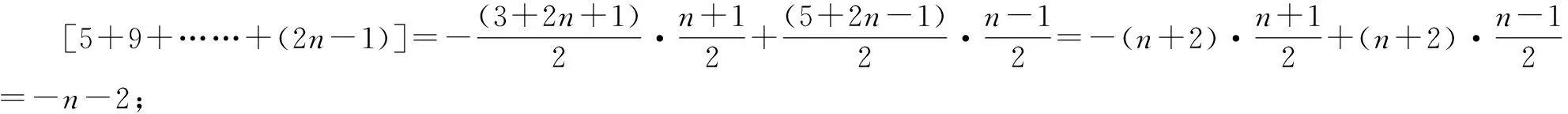
当n为偶数时,
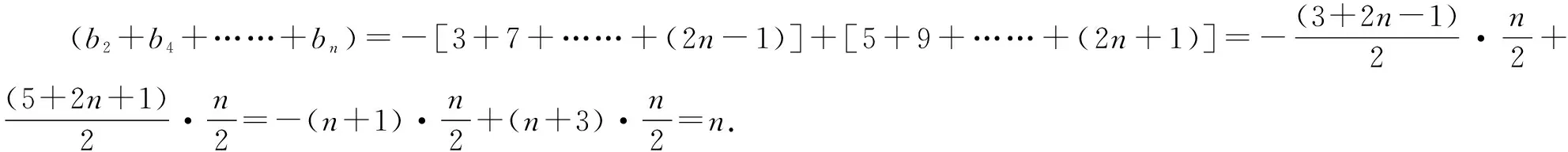
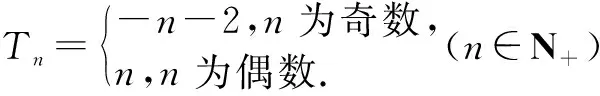
生3:还可以用并项求和法.下面以n为奇数为例.
当n为奇数时,Tn=(b1+b2)+(b3+b4)+……+(bn-2+bn-1)+bn.
师:如果我们留下的是首项,可不可以?
Tn=-3+(5-7)+(9-11)+……+(2n-1-2n-1)
最后的结果也正确,相比较而言,留首项会比留末项好一些,特别是当末项不容易化简的时候.
设计意图:复习数列分奇偶项求和的两种常见方法,即分组求和法与并项求和法.如果运用并项求和法,讨论n为奇数时,要考虑剩下的一项,不要遗漏,建议留下首项.如果求和结果是分奇偶的,要记得用分段数列形式表示.
第三环节:反馈训练.
变式1已知cn=(-1)n·2n,求数列{cn}的前n项和Sn.
师:这个题目,大家可以先对n分奇偶,再分组求和或者并项求和,做法如下:
当n为奇数时,
Sn=-(2+23+……+2n)+(22+24+……+2n-1)
当n为偶数时,

其实,我们也可以把数列{cn}整理成cn=(-2)n,直接代入等比数列的前n项和公式中,得到
Sn=(-2)+(-2)2+(-2)3+……+(-2)n
师:特别注意,如果cn=(-1)n-1·22n+1怎么办?
学生思考,讨论.
师:把{cn}变为cn=8·(-4)n-1(n∈N+)即可.
师:如果把题目变成cn=cosnπ·2n-1(n∈N+),那怎么处理?
生4:cn=cosnπ·2n-1看成cn=(-1)n·2n-1.
师:是的,非常正确.
设计意图:设置这个题,让学生感受数列分奇偶项求和与等比数列相结合时,可以选择分奇偶,用分组求和或者是并项求和,当然也可以转化为等比数列求和,比较简洁.注意引导学生将题目条件等价转化为熟悉的情境进行求解.
第四环节:巩固提升.
变式2已知cn=(-1)n·n·2n,求数列{cn}的前n项和Sn.
思路分析:设置这个题,让学生感受数列分奇偶项求和与等差乘以等比数列相结合时,要尽量转化为等比数列求和,比较简便.
师:有同学能解决这个问题的吗?
生6:把(-1)n·2n看成(-2)n,利用错位相减法.
Sn=1×(-2)1+2×(-2)2+……+n×(-2)n
①
-2Sn=1×(-2)2+2×(-2)3+……+n×(-2)n+1
②
由①-②,可得
3Sn=1×(-2)1+1×(-2)2+1×(-2)3+……+1×(-2)n-n×(-2)n+1.

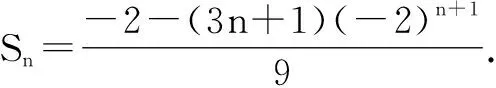
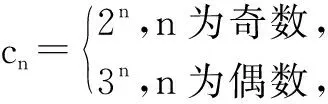
师:这个题目要求{cn}的前2n项和S2n,就不用对n进行分类讨论了.
由题意可得,
S2n=c1+c2+……+c2n-1+c2n
=(2+23+……+22n-1)+(32+34+……+32n)
验证当n=1时,S2=11=c1+c2,符合题意.
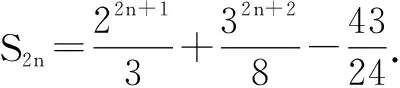
4 结语
“好的例题教学就是照亮学生解题的灯塔.”那么一名好教师,就是自己沉入题海,帮助学生浮出题海的人.一节课45分钟的时间,应该是教师与学生共同碰撞与促进的过程,好的例题与变式,能够发展学生思维,促进提升数学素养.
