重视核心素养 凸显数学本质
——以2022年新高考数学Ⅰ卷为例
2023-01-11江苏省如东高级中学
江苏省如东高级中学
葛张勇
“2022年高考数学落实立德树人的根本任务,促进学生德智体美劳全面发展,体现高考改革的要求.”教育部教育考试院命题专家对今年高考数学试题进行了评价.同时指出,试卷在考查学生基础知识和学科能力的同时,尤其突出对数学核心素养和学习能力的考查,体现了很好的选拔功能.
《普通高中数学课程标准(2017版2020修订)》指出:“引导教学更加关注育人目的,更加注重培养学生核心素养,更加强调提高学生综合应用数学知识解决实际问题的能力,把握教学的深度和广度,为阶段性评价、学业水平测试和升学考试命题提供重要依据.”下面以2022年全国新高考数学Ⅰ卷为例,谈谈新高数学试卷核心素养的考查,旨在抛砖引玉.
1 重视本质,把握数学抽象的思维方式
数学抽象是根据研究对象的数量及图形关系,结合已有的数学知识抽象出数学概念及数学模型,进而用数学知识、数学思维分析解决问题.其抽象方法有性质抽象、关系抽象、变换抽象、类比抽象等,数学抽象是数学产生和发展的思维基础,凸显了数学本质.

C.f(-1)=f(4) D.g(-1)=g(2)
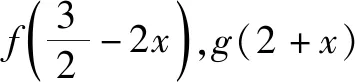
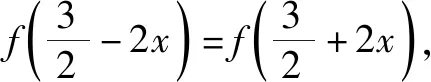
所以g(-1)=g(1)=-g(2),故选项D错误;
若函数f(x)满足题设条件,则函数f(x)+C(C为常数)也满足题设条件,所以无法确定f(x)的函数值,故选项A错误. 故选:BC.
解法二:化抽象为具体,令函数f(x)=sin πx+1,则g(x)=πcos πx,符合题意.故选:BC.
点评:解法一的关键是转化题干条件为抽象函数的性质,准确把握原函数与导函数图象间的关系,把握函数的奇偶性等性质(必要时结合图象)即可得解;解法二是从一般到特殊.
2 归纳演绎,培养逻辑推理的探索品质
逻辑推理是指借助问题的条件以及数学概念、定理,通过条件之间的关联从而得到新的结论或者新的命题.它包括从特殊到一般以及从一般到特殊两类推理方式,是数学学习中不可缺少的一种素养.

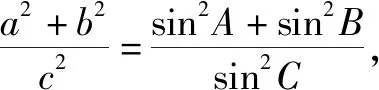
点评:三角函数化简的核心逻辑是“化同”,即角的“化同”和函数名的“化同”.既要知道公式、定理、解法是什么,还要知道解题的动机和时机、解题逻辑是什么,以逻辑驭解法,以解法促逻辑.
3 创设情境,构建数学建模的应用意识
数学建模是根据所学数学知识解决实际问题的素养,它是数学抽象、逻辑推理、数据分析和运算等其他核心素养的集中体现和升华.数学建模通常包括模型分析、模型建立、模型求解、模型检验等步骤.

A.1.0×109m3B.1.2×109m3
C.1.4×109m3D. 1.6×109m3
解析:依题意可知棱台的高为MN=157.5-148.5=9(m),所以增加的水量即为棱台的体积V.
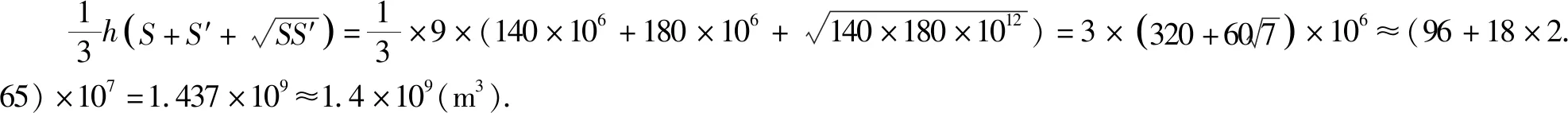
故选:C.
点评:本题建模容易.两点易错,一是棱台的体积公式,二是棱台的高与什么关系最密切.在题干的提示下估算还可以优化估算的次数.《普通高中数学课程标准(2017版2020修订)》第27页明确提出,知道球、棱柱、棱锥、棱台的表面积和体积的计算公式,能用公式解决简单的实际问题.
4 数形结合,提升直观想象转化能力
《新课程课程标准》指出:“直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.”直观想象的素养体现的是数形结合的重要数学思想.以形助数,挖掘图形性质,是高考数学常见的优化运算策略.
例4(2022年新高考Ⅰ卷第14题)写出与圆x2+y2=1和(x-3)2+(y-4)2=16都相切的一条直线的方程.
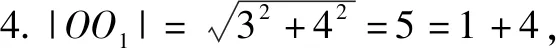

图1
点评:本题挖掘图形性质,优化解题策略.教学中引导学生探索数学知识的几何背景,增强运用几何直观解决问题的意识,提高学生数形结合解决问题的能力,从而提升直观想象的核心素养.考场上处理此类开放性试题选择一个最简单结果即可.
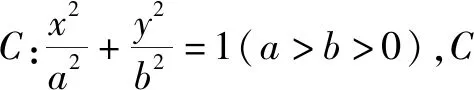
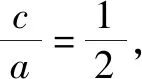
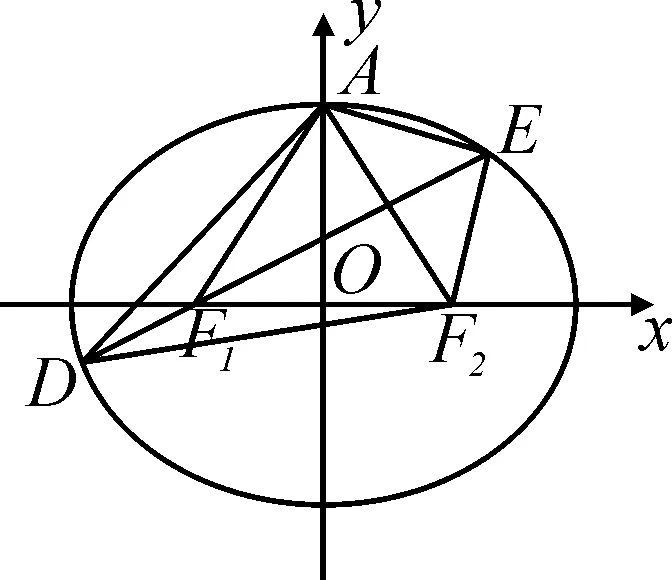
图2
点评:本题的几何法,即对称性+椭圆定义将挖掘图形几何性质体现得淋漓尽致.
5 数据分析,助力数学运算的核心素养
数据分析是从研究对象中获取关键数据,应用数学方法对数据进行量化分析,形成研究对象的定量分析结果.数据分析是研究随机现象的重要数学技术,与数学抽象、数学建模、逻辑推理、数学运算等核心素养之间密不可分.
数学运算是六大核心素养中极其重要的一个,在数学学习中起着重要作用,它是解决数学问题的重要手段.数学运算不是简单的数学计算,它反映了一定的综合能力,需要在解决问题中确定运算目标,探究运算思路,设计运算程序,依据运算法则正确解答.
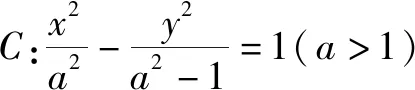
(1)求l的斜率;
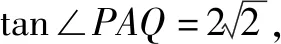
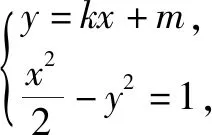
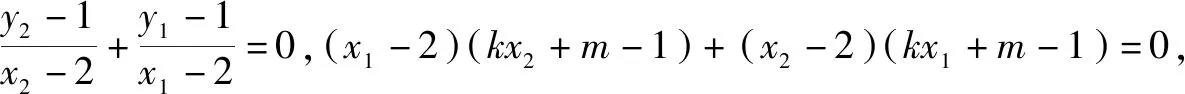
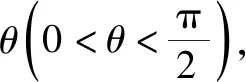
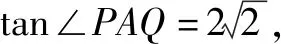
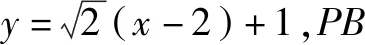
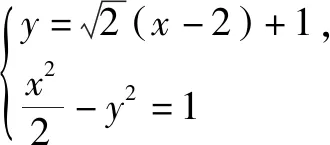
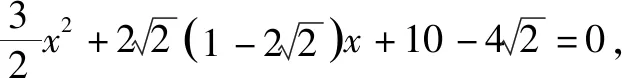
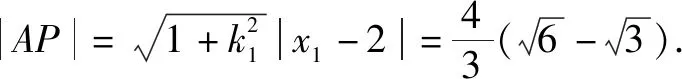
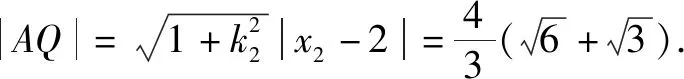
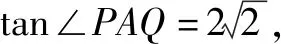
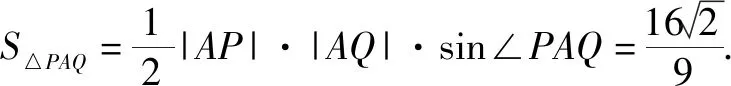
点评:无运算不数学,数学运算是解决数学问题的关键环节.高考对数学运算要求越来越高.本题无论用什么方法解决,较复杂的运算都不可避免.教师在教学中既要注重解题思路、方法的探究和设计,也要在具体运算过程中做示范和引领,帮助学生感受反思解题运算的方法和技巧,优化解题运算,培养学生处理数学运算的耐心、细心及必胜的信心.
