基于流-固-热耦合的超声速弹箭尾翼强度分析

向 熙,封 锋,陈 超,王明亮,罗 飞

(1.南京理工大学 机械工程学院,江苏 南京 210094;2.安徽神剑科技股份有限公司,安徽 合肥 230601)

尾翼是尾翼式火箭弹的稳定装置。在设计阶段,既要保证尾翼具有一定的结构强度,防止尾翼受空气动力而失效,又要控制尾翼质量[1]。因此,设计尾翼时应对其进行校核,传统的校核方法是将空气动力等效为面均布载荷作用于翼片表面,再将翼根与弹身铰接处设为固定约束,根据结构静力学方法计算翼片的变形和应力[2]。但实际飞行过程中翼片各点处的载荷不同,且在高速飞行过程中空气会对弹身持续加热,使弹身的温度升高,进而在一定程度上改变材料的力学性能。因此按传统校核方法计算的结果与实际结果会有一定偏差。

本文以122 mm火箭弹为研究对象,首先根据火箭弹的飞行条件,对外流场进行稳态计算,得到弹体外表面的气体温度、压力等气动力参数。在此基础上对弹体进行瞬态耦合传热计算,传热计算完成后,根据翼片上的温度分布,调整材料的力学性能参数,并将流场计算得到的壁面压力导入静态结构模块,计算翼片在对应飞行工况的温度和压力作用下产生的应力和变形。本文的耦合计算中考虑了温度变化对材料力学性能的影响,并查找了材料的强度随温度变化的模型,使得计算应力与变形时结果可信度更高,分析过程具有一定创新性。

1 模型及参数

1.1 物理模型与材料设置

火箭弹全弹外形如图1所示,全弹长2 994 mm。弹身最大直径为122 mm。稳定装置为6片直尾翼,翼片的尺寸参数如图2,翼片与弹轴有0.8°的斜置角。

图1 全弹外形尺寸参数Fig.1 Schematic diagram of the rocket

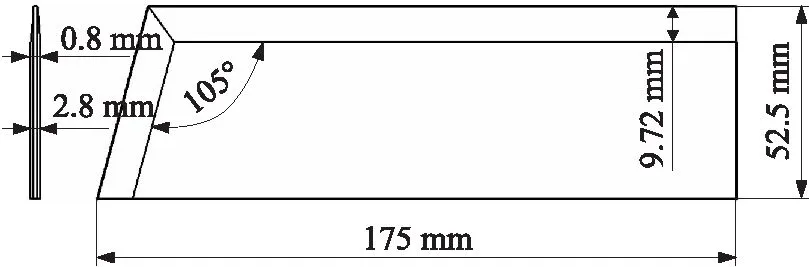
图2 翼片尺寸参数Fig.2 Schematic diagram of the rocket tail

弹身材料为钢,尾翼所用材料为铝合金。铝合金的防火性能较差,当温度升高时,材料的强度和弹性模量降低,200 ℃时,结构用铝合金的强度开始明显下降;300 ℃时强度下降到常温下强度的50%以下;温度达到550 ℃时,结构用铝合金的强度和弹性模量基本丧失[10]。

国内对高温下铝合金性能的研究较多,但定量给出铝合金强度与温度关系模型的较少。文献[11]通过试验获得了6061-T6铝合金在不同温度下的弹性极限和抗拉强度,并根据试验结果采用三项式拟合得到了6061-T6铝合金在温度为10～550 ℃条件下的弹性极限模型和抗拉强度模型,表达式为

(1)

(2)

(3)

式中:T为温度,℃;fp,T、fu,T、和ET分别是温度为T时铝合金的弹性极限、抗拉强度和弹性模量;fp、fu和E0分别是常温下铝合金的弹性极限、抗拉强度和弹性模量。本文取fp=280MPa,fu=310MPa,E0=72 GPa。本文根据该模型计算一定温度下的铝合金力学性能参数,然后根据翼片上温度载荷的大小赋予材料相应的力学参数。

1.2 计算域及边界条件设置

流体计算域为圆柱形,前端距弹头为8倍弹径,后端距弹尾为15倍弹径,直径为20倍弹径。经过网格无关性验证,确定流体域网格如图3所示,固体域网格如图4所示。

图3 流体计算域及网格Fig.3 Fluid domain and grids

图4 固体域及网格Fig.4 Solid domain and grids

流体域稳态计算时,弹体外表面设置为绝热壁面,计算域外表面设置为压力-远场边界。来流速度的变化情况为Ma=1.1、1.5、2、2.5、3、4、4.5、5和5.5。由于火箭弹只在初始阶段有较小幅度的攻角变化,本文的所有计算工况攻角均设置为0°,其他气体动力学参数主要受火箭弹的飞行高度影响。

图5分别为火箭弹的速度-时间和高度-时间曲线,由此可根据来流速度得到对应的飞行高度。同一速度对应几个飞行高度时,取弹道曲线曲率较小处的值。由于该弹道曲线的最大速度约1 200 m/s,当Ma>3.5时,飞行高度取为1 000 m,分析结果仅作为高马赫数飞行时的参考。确定飞行高度后,根据国际标准大气,由文献[12]确定该高度下空气的温度,压力和密度;由萨瑟兰公式确定该条件下的空气动力黏度。

图5 火箭弹速度-时间和高度-时间曲线Fig.5 Velocity-time and height-time of the rocket

瞬态传热计算时,将绝热壁面更改为耦合传热壁面,弹身材料设置为钢,弹翼材料设置为铝合金。

静力学计算时,根据传热计算的温度结果修改铝合金的力学性能参数,并将流场计算得到的壁面压力作为载荷导入固体域,由于与翼片相比,弹身的变形可忽略不计,将弹身圆柱面设为固定约束,据此求解尾翼上的变形和应力。

2 耦合方法及控制方程

2.1 耦合方法

按数据的传递方式,流固耦合分析可分为单向耦合与双向耦合[13]。本文中固体的变形属于小变形,对流场的影响可以忽略,故采用单向耦合分析求解。

2.2 控制方程

根据本文的来流速度与模型参数,计算外流场雷诺数,由于流动雷诺数大于临界雷诺数,选择湍流模型。k-ω改进后的SSTk-ω模型结合了自由流的k-ε和近壁面处的k-ω模型,求解壁面处的流动更加准确。本文计算气动加热对弹箭尾翼的影响,考虑到计算成本和适用性,选择更适合计算壁面传热的SSTk-ω模型。

流体域控制方程为

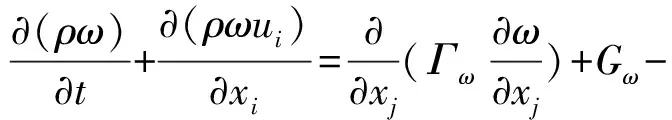
(4)

(5)

p=ρRTf

(6)

式中:xi为坐标分量,ui为速度分量;Gk为层流速度梯度产生的湍流动能;Gω为ω方程产生的湍流动能;Гk和Гω为k和ω的扩散率;Yk和Yω为k和ω的发散项;Dω为正交发散项;Sk和Sω为湍流源项[14];Tf为流场温度。

固体域控制方程为弹性力学基本方程,包括平衡方程、几何方程、应变协调方程和本构方程,用张量形式表示为

σij,i+fi=0

(7)

(8)

εij,kl+εkl,ij-εik,jl-εjl,ik=0

(9)

(10)

式中:σ、ε、w分别代表应力、应变和位移;f代表外力;E和ν分别为弹性模量和泊松比[15]。

3 计算结果及分析

3.1 稳态计算结果及分析

Ma=4时流体域的速度云图如图6所示。来流流经弹头时气流被压缩,引起头部流速降低,压力升高,形成弹头高压区。由于超声速来流的作用,弹头部形成强度较大的斜激波,在头部与弹身连接处,气流发生膨胀,形成紧贴斜激波波后气流的膨胀波,膨胀波内气流压力降低,流速增大。翼片与弹尾处同样形成了斜激波和膨胀波,斜激波的锥角与头部斜激波锥角相同,而膨胀波内气流流速大于弹体前部膨胀波内的气流流速。弹尾后产生锥形涡旋,形成底阻,涡旋后气流流速逐渐增大。

图6 流场速度云图Fig.6 Flow field of the rocket

对Ma=4.5以下的工况绘制阻力系数曲线,并与风洞数据对比,结果如图7所示。由图可知,大部分工况下仿真得到的阻力系数与风洞试验得到的值较接近,平均误差小于5%。可以认为流场仿真的结果与实际流场情况较接近,流场计算结果具有一定正确性。

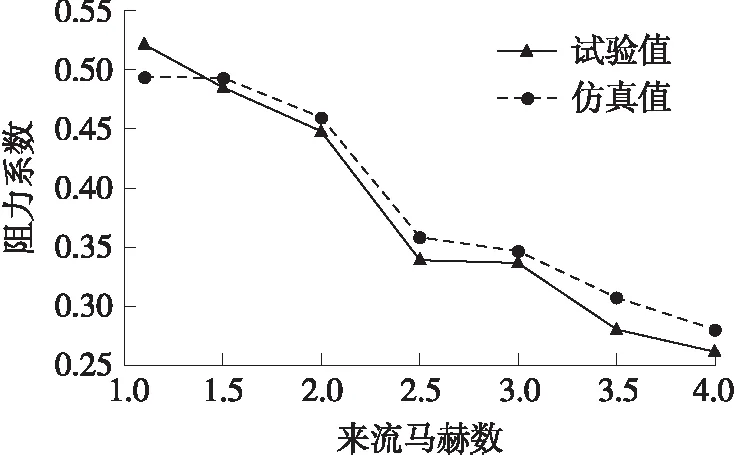
图7 阻力系数与试验值对比Fig.7 Comparison of drag coefficient

3.2 瞬态传热结果及分析

外流场稳态计算收敛后,将壁面设置为耦合壁面,进行瞬态传热计算。考虑到实际飞行时工况变化和计算量的因素,每种工况下只进行2 s内的传热计算。图8为Ma=4时,2 s内翼片剖面的温度分布变化。

图8 翼片2 s内瞬态传热Fig.8 Transient heat transfer of the rocket tail in 2 s

由图可知,由于超声速来流受到前缘翼尖的阻碍而速度骤减,该处流场温度急剧升高,因此整个翼片上前缘翼尖最先开始升温。若在此之前无温度累积,0.5 s时翼尖温度将由常温升高至390 ℃。1 s时,前缘翼尖处最大温度达590 ℃,温度向内传递,整个翼尖温度超过330 ℃。1.5 s时,除少部分区域外,整个翼片温度都超过了350 ℃,前缘的局部区域温度已超过630 ℃。不考虑热防护时,该区域已达到铝合金熔点。受到高速气流的冲刷作用,前缘翼尖材料将会因烧蚀而脱落,导致翼片面积减小,气动性能降低。2 s时,翼片整体温度高于430 ℃,且温度超过630 ℃的区域进一步扩大。这表明,火箭弹在高马赫数下飞行时间越长,翼片烧蚀越严重。铝合金材料将由前缘翼尖向翼根和后缘方向逐步脱落,导致其功能性降低,从而引起弹的稳定性下降。图中弹身的升温明显低于弹翼,这是因为钢的热导率约为铝合金的十分之一,温度变化率更小。

图9为各工况下传热2 s后,翼片剖面的最高温度随来流的变化。由图可知,当火箭弹飞行速度越高,翼片上的最大温度也越高。当Ma≤2时,翼片最大温度受Ma变化的影响较小。随着速度增大,翼片最大温度的增幅变大,且差值也逐渐增大。本文研究的尾翼材料在无热防护处理的条件下,在550 ℃时弹性模量和强度基本丧失,在660 ℃时达到熔点。在最高温度曲线上分别对应Ma=3.4和Ma=3.7。因此,若火箭弹以Ma>3.4的速度飞行。则尾翼将会在短时间内出现严重变形进而导致气动性能下降;若以Ma>3.7的速度飞行,尾翼会在短时间内达到熔点。此时在气流作用下尾翼会出现材料脱落,当前缘翼尖脱落后,在脱落位置会形成新的前缘翼尖,使得脱落会从翼尖开始,沿后缘和翼根进行,从而形成较为严重的热烧蚀。

图9 传热2 s时翼片最高温度Fig.9 Maximum temperature of the rocket tail at 2 s

图10为某次飞行试验后翼片残骸的烧蚀情况[16]。模型与本文所用翼片模型基本相同,材料为无热防护处理的铝合金,最大飞行马赫数4.5。可以看到,翼片前缘出现了较为严重的烧蚀,其中前缘翼尖部分材料已脱落,烧蚀位置与本文仿真分析的结果较为吻合。一定程度上说明了本文仿真结果的正确性。实际中弹箭在高超声速飞行时,其飞行高度可能已经超过1 000 m,由于空气密度、压强、温度和粘度等随高度增加而下降,气流摩擦与近地面飞行相比更小,且尾翼会在结构或材料上做热防护处理,所以温度累积可能会低于本文的分析结果。

图10 某飞行试验后翼片烧蚀情况[16]Fig.10 Ablation of the rocket tail after flight test

3.3 固体域结果及分析

将流场计算结果中的壁面压力作为载荷导入固体域中。Ma=3工况下翼片上导入的结果如图11所示。由图可知,最大压力出现在翼片前缘,约为1.2 MPa,并由翼片前缘向后缘迅速减小。除前缘的局部区域,其他区域压力与远场压力基本相等。翼片前缘翼尖同时是温度最高和承受压力最大的位置,所以实际中该位置最容易被破坏。由于结构和来流的对称性,每个翼片的压力分布相同。

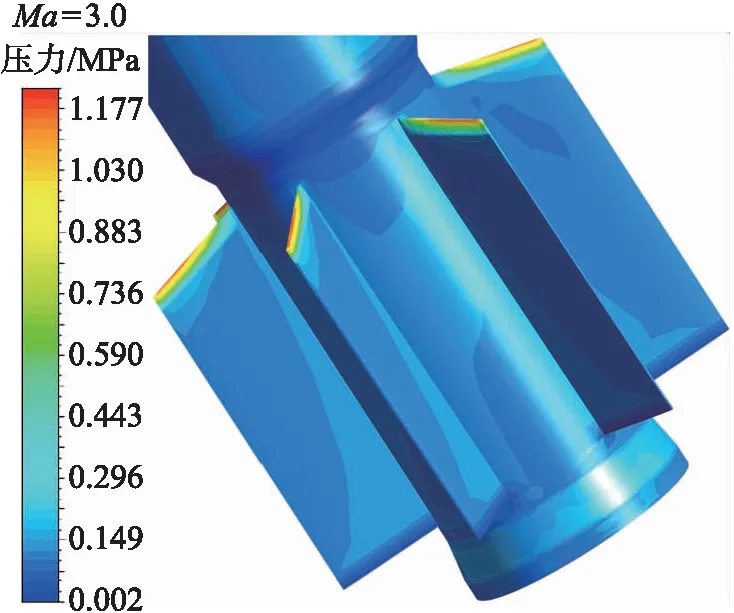
图11 翼片表面压力Fig.11 Surface pressure of the rocket tail

将弹身设为固定约束,求解该压力作用下翼片的变形和应力。Ma=3工况下翼片变形和应力分布如图12所示。因为翼根与弹身连接处为固定约束,所以翼根处变形量为0,在空气动力作用下,从翼根到翼梢,变形量逐渐增大,从翼片后缘到前缘,变形量也逐渐增大,翼片前缘翼尖处出现最大变形,为0.077 mm。等效应力则从翼根到翼梢逐渐减小,从翼片前缘到翼片后缘逐渐减小,最大应力位于翼根靠近前缘处,为7.76 MPa。

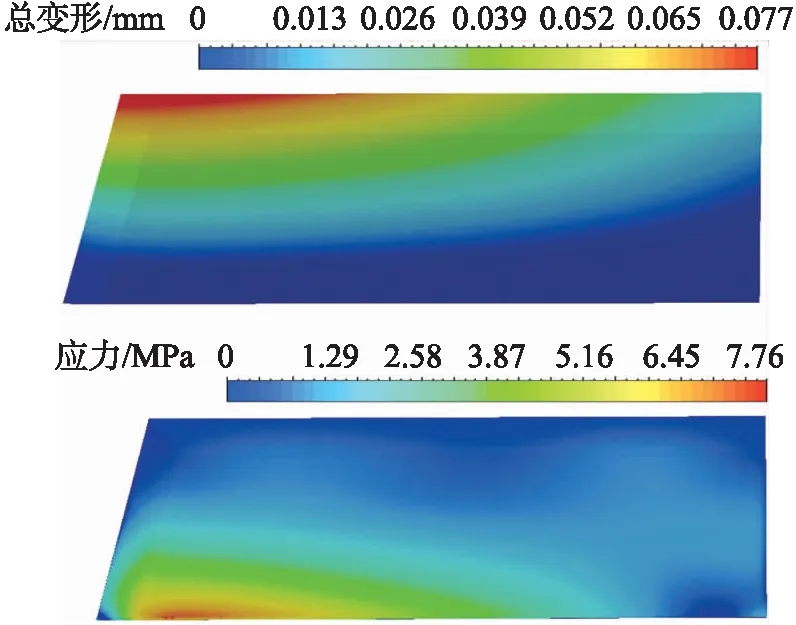
图12 翼片变形与应力云图Fig.12 Deformation and stress of the rocket tail

温度对翼片最大总变形量和最大等效应力的影响如图13和图14所示。由于Ma>3.5时,考虑温度影响,翼片材料的弹性模量和强度已基本丧失,所以没有计算此条件下的应力和变形。由图可知,尾翼受气动力作用产生的变形和应力随来流的增大而增大。当Ma<2时,温度对翼片的变形影响较小。而当Ma>2时,考虑温度影响计算出的变形量明显大于不考虑温度影响计算出的相应值。Ma=2.5时,考虑温度影响计算出的变形量是不考虑温度影响变形量的1.2倍,Ma=3时是其1.5倍。主要原因是弹的飞行速度增大到一定程度后,弹翼上温度较高,与常温条件相比,材料的弹性模量急剧下降,承载能力随之降低,在相同的气动压力下会出现严重变形。

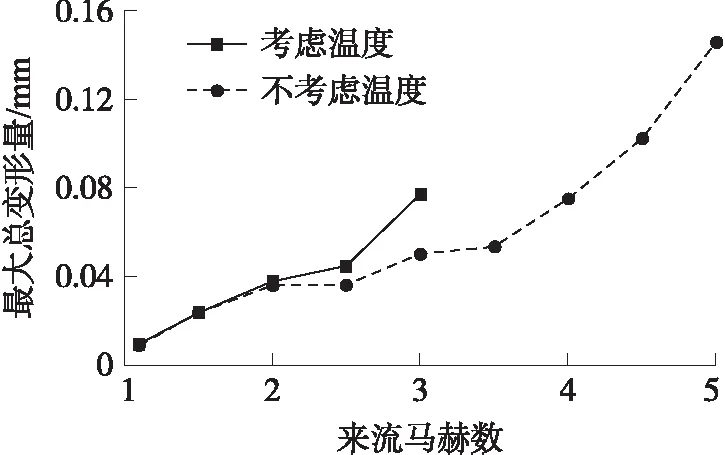
图13 最大总变形量随来流速度的变化Fig.13 Maximum total deformation-velocity curve of the rocket tail

图14 最大等效应力随来流速度的变化Fig.14 Maximum equivalent stress-velocity curve of the rocket tail

随着飞行速度的增加,考虑和不考虑温度影响计算出的应力值基本相等,表明温度对应力的影响较小。当3

4 结论

采用流-固-热耦合的方法对某火箭弹尾翼进行了强度和安全性分析。结果表明:

①当火箭弹在0°攻角下以一定速度持续飞行时,翼片上的温度将在短时间内迅速升高,且速度越大,升温越剧烈。前缘翼尖温度最先开始上升,热量由前缘、后缘和翼尖逐渐向内部传递,经较短的时间形成前缘部分区域内温度最高,靠近翼根的部分区域温度相对较低的现象。

②尾翼上的气动压力集中在翼片前缘部分区域,其他区域压力远低于前缘压力,使得前缘翼尖同时是受热和受力最大的位置,所以实际中前缘翼尖是最容易发生破坏或失效的位置。

③在温度和压力的作用下,翼片会发生变形且内部会产生应力,最大变形出现在前缘翼尖,向后缘和翼根方向逐渐减小;最大应力出现翼根靠近前缘的位置,向后缘和翼尖方向逐渐减小。温度对应力影响较小,对变形量的影响则随来流速度增大而增大,原因是温度升高导致了材料的力学性能下降。

④持续以高超声速飞行的弹箭,若无热防护处理,翼片温度会在短时间内剧烈增加,使材料丧失其弹性模量和强度甚至熔化,从而降低或丢失结构的气动性能,因此必须在材料或结构方面进行热防护处理。