基于优化变权组合模型的配电网中台区负荷波动范围预测研究
2023-01-11李鸿奎彭红霞李福建乔朋利
李鸿奎,彭红霞,踪 凯,李福建,乔朋利
(国网山东省电力公司 菏泽供电公司,山东 菏泽 274000)
负荷预测是配电网台区管理中的关键部分,由于干扰的随机性与时变性导致负荷产生大幅度波动[1-2],此波动人工无法控制。与此同时,电网的平稳运转取决于电力系统发电机组输出功率和电力负荷的持续性均衡[3]。电网台区网络架构相对薄弱,负荷波动会致使电网频率产生振荡,影响电力输出稳定性,损坏台区设备[4],精准预测台区负荷波动范围,是确保配电网正常运行的重要手段。
许言路等[5]引入全卷积网络结构和因果逻辑约束增强时间序列特征表达,通过多尺度卷积计算不同长度时域数据相互关系,设计残差网络结构增加网络深度,增强预测正确率。但方法对线性时域数据拟合程度很差,预测结果极易产生误差;李焱等[6]分析电力系统负荷周期性、天气相关性等特征,采用C均值模糊聚类算法聚类历史样本,将同类数据看作训练集样本,创建决策树,得到预测结果后运用粗糙集理论修正负荷预测结果。但该方法预测结果的偏差存在一定的偶然性,不同应用环境下的精准度水准有待提升。
总结以上负荷检测研究中出现的实际问题,本文提出一种基于优化变权组合模型的配电网中台区负荷波动范围预测方法。首先对采集到的负荷波动数据实施小波去噪,消除复杂的冗余数据,克服传统单项预测模型弊端,使用优化变权组合模型完成负载波动范围预测任务。在仿真实验中,充分证明了本文方法在计算精度、效率等方面的可靠性,可广泛应用于现实场景中。
1 负荷波动数据消冗
分析台区系统负荷特征时,电力负荷信号为处于变化电压上的时间序列,具有干扰性强、频谱范围广的特性[7]。本文引入小波去噪策略,有效剔除配电网台区负荷数据中干扰向量,为波动范围预测工作提供干净的数据,确保预测输出结果准确性。
1.1 变权组合模型
本文参考刘明等[7]设计的基于变权组合模型的中长期负荷概率密度预测方法,构建变权组合模型,平均赋权组合模型预测值的计算公式为:

(1)
假设对于同一预测问题有n种不同的单一模型,fi(xi)为第i种模型在t时刻的预测值;fi(xt)为组合模型在t时刻的预测值。
1.2 小波分析的变权组合模型优化
考虑负荷信号数据的横、纵向连续性数据特征[8],通过设定阈值来提升去噪效果。假如阈值过小,则会保存很多小波系数,但去噪效果并不理想;假如挑选的阈值很大,噪声就会变小,但会过滤掉数据内的高频信息[9]。这里使用固定阈值门限准则来明确阈值的门限值T。
以往的阈值函数被划分成硬阈值函数与软阈值函数[10],硬阈值的衡量标准是:保留不低于阈值的小波系数,将低于阈值的小波系数设置为零,其数学解析式为:
(2)
利用小波分析方法对变权组合模型进行优化,软阈值的衡量标准是:将小波系数内低于阈值的数值设定为零[11],把不低于阈值的与阈值相减,得到:

(3)


图1 软、硬阈值函数曲线示意Fig.1 Diagram of soft and hard threshold function curve
所以在此基础上,将小波分析去噪的具体过程分为如下步骤:①挑选待预测日前n天每天96点负荷波动数据与气象数据,将其看作数据样本,构成一个二维数据集,并采取归一化处理;②小波分解数据集,得到小波系数ωj,k,重构负荷信号;③对重构后的去噪信号采取反归一化计算,最终获得没有冗余信息的负荷波动数据。
2 台区负荷波动范围预测
优化变权组合模型是融合多种预测算法,最终构成的一种全新预测方法,和其他方法相比,优化变权组合模型能采集更全面的目标信息,克服了单项预测在计算精度方面的不足[13-15]。


(4)

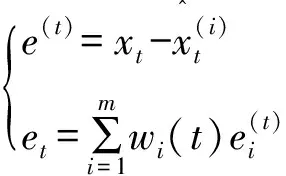
(5)
优化变权组合模型进行负荷波动范围预测最核心的问题就是变权重的挑选[16]。一般情况下,使用预测偏差平方和来定义预测准确性,但在计算中会出现以下问题:假如负荷波动数据内拥有异常值,那么异常点位置的数据会存在较大偏差[17-19],通过平方处理后,偏差值会随之增大,获得的权重遭受异常值影响的概率也会增多,在一定程度上会忽略其他的关键负荷信息,但消除异常点又有可能形成可靠数据的丢失。将组合预测偏差的最低绝对值作为计算原则,在符合权重系数自身需求前提下[20],得到最优权重公式:

(6)
式中,yt为预测偏差绝对值。
选择1个组合预测第t个时段预测偏差et的目标函数g,把台区负荷波动范围预测模型表示成:
(7)
3 算例分析
将某市的某台区2017年1月至2020年12月的历史负荷数据和气象台提供的气象数据当作实验数据,在Matlab软件中,使用本文方法、卷积神经网络法和随机森林法进行仿真实验。
将2017年1月至2019年12月数据看作训练集,训练集的数据特征包含月最高负荷值、月高温均值、月低温均值、年份与月份。预测2020年1—12月的台区负荷波动范围,将2020年1—12月的日期、气象信息、历史月度最高负荷作为输入值,输出数据是2020年每个月份的负荷波动范围预测值。设置数据的输入特征数据x1—x5依次表示年、月、月高温均值、月低温均值和历史月度最高负荷,数据的输出特征y表示当月最高负荷。
使用Spearman相关系数ρ剖析年、月、月高温均值、月低温均值、历史负荷值和台区负荷波动范围之间的关联性,计算公式为:
(8)

若|ρ|<0.4,表明为弱相关关系;0.4≤|ρ|<0.8,表明为中度相关关系;|ρ|≥0.8,呈现出强相关关系。
将平均误差百分比与决定系数R2作为方法预测性能的评估指标,平均误差百分比数值越低,表明预测结果精度越高,决定系数描述了真实值和预测值之间的关联水平,系数值越趋近于1,表明计算结果拟合精度越好。指标定义:

(9)

(1)获取目标年 2025 年的负荷密度分布情况。当同一用地类型负荷同时考虑分布式光伏出力、电动汽车充电以及传统用电负荷进行分析是需要同时考虑各场景的相互影响。利用负荷空间负荷预测方法对目标年进行预测,其目标年2025年的负荷密度分布如图2所示。
元胞区域过多无法枚举,随机选取M区的典型元胞R15 为例进行分析,在目标年用地类型所选元胞仅包含商业、居民、公共 3 类用地;仅包含 6 个配变台区。

图2 目标年 2025 年的传统负荷密度分布Fig.2 Traditional load density distribution in 2025
(2)确定台区负荷波动范围影响系数。利用公式推算台区月最高负荷波动和不同影响元素的Spearman相关系数,结果见表1。

表1 相关性计算结果Tab.1 Correlation calculation results
观察表1可知,年份、月高温均值、历史负荷值与台区负荷波动拥有很强的相关性,因此进行预测工作时,要详细收集以上3类气象数据,才能最大限度地保证台区负荷波动范围推导结果的可靠性。
(3)确定配变台区以及用地类型面积。结合表1 相关性计算结果与 2025 年用地性质规划,可得到的配变台区以及用地类型面积,见表2。

表2 配变台区以及用地类型面积Tab.2 Distribution substation area and land type and area
将所有元胞都以上述方式进行分析可以得到各月各场景的协调系数,且各元胞包含多个用地类型依据配变台区提取方法和预测方法对目标年2025年的传统负荷密度进行预测,并通过各月各场景的负荷协调系数得到各元胞多场景负荷密度,各元胞多场景负荷密度乘以各元胞对应的面积得到目标年总量负荷值。
(4)通过计算得到本文方法预测性能。为充分研究本文方法预测成效能否满足预期要求,运用平均误差与决定系数评估指标,计算本文方法的预测性能,仿真结果如图3、图4所示。
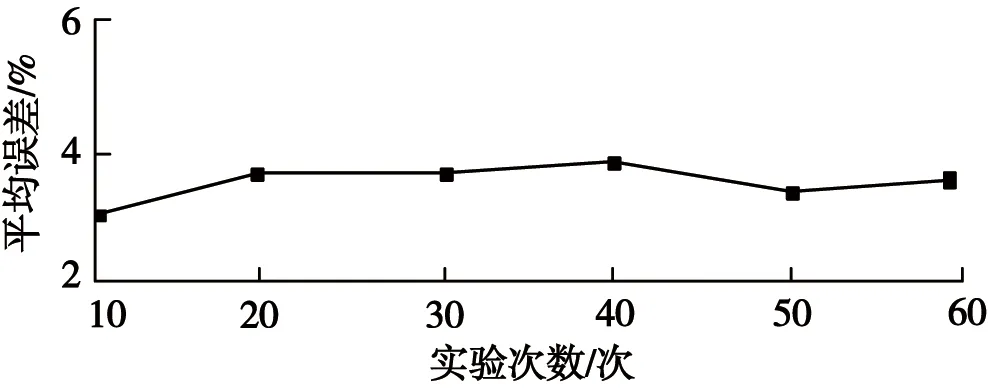
图3 本文方法平均误差Fig.3 Average error of this method

图4 本文方法决定系数值Fig.4 Determination coefficient value of this method
分析图3可知,实验次数为10次时,本文方法的平均误差为3%,实验次数为30次时,本文方法的平均误差为3.9%,实验次数为50次时,本文方法的平均误差为3.7%;本文方法的平均误差明显低于其他方法。分析图4可知,实验次数为10次时,本文方法的决定系数值为0.96,实验次数为15次时,本文方法的决定系数值为0.97,实验次数为25次时,本文方法的决定系数值为0.98。
综上可知,本文方法的预测误差较低,决定系数值最接近1,输出结果的准确性较高,具备更优的负荷波动范围预测能力。出现此种现象的原因在于,本文方法在剔除冗余负荷数值前提下,以预测偏差最低绝对值为推导原则,运用优化变权组合模型弥补单项预测的缺陷,获得高精度负荷波动结果,为配电网台区管理工作提供有效电力参考信息。
4 结论
配电网台区负荷波动范围预测对电力系统控制、运行安全及优化调度等方面都具有极其重要的现实意义,本文立足电力负荷波动规律,提出一种基于优化变权组合模型的配电网中台区负荷波动范围预测方法。所提方法简单易行、预测效率较快、预测精度也远优于传统单项模型预测方法,为台区潜在安全隐患检修提供借鉴与参考。未来在台区负荷波动范围预测问题中,会适当引用个体学习器集成方法,进一步优化预测结果真实性与可用性。
