基于多元散射校正的中药材种类鉴别

金莹，何蔚娟

（1.咸阳职业技术学院 机电学院，陕西西安，712000； 2.三原县农业科学技术中心，陕西三原，713800）

1 概述

在我国，传统中药针对材病理治疗的针对性上讲究地道药材。同一种药材在特定的自然条件和生态环境下会表现出不同的药理特性，其在针对患者的医疗效果上也会表现出不同的治疗效果。因此，对于同种药材的混合鉴别就成为我国研究者进行药材分类研究的热点。张鹏琴[1]提出一种基于监督局部线性嵌入和判别分析气味数据分析方法，该方法将不同种类的中药材及不同产地的何首乌进行分类鉴别。但该方法在使用没有全局考虑中药材的药理特性。郝丹丹[2]研究了一种实时快捷的药材鉴定方法，实现了短时间对同一地区不同植物的判别。而该方法对不同产地药物分类具有一定的局限性。因此，丁学利[3]研究运用标准差法分别提取特征波段，将中药材的中红外和近红外两种红外光谱的特征波段数据合并后，采用Fisher判别分析法，对组别进行合理的分类，正确率达到98.4%。由于在基于Fisher方法判别的过程中，要进行反复试错理论，增加了算法的复杂度。冯炜思[4]利用短的DNA序列，对某个或者某些相关的基因进行大范围的扫描，实现对中药材分类鉴别。王静[5]基于中红外光谱数据，采用导数光谱法、标准正态变量变换和多元散色校正等预处理方法并依据标准差法提取特征波段，通过线性判别分析、支持向量机、集成学习三种有监督分类模型与处理后的数据进行交叉组合鉴别，快速准确鉴别中药材产地。以上两种方法在理论研究及实际应用上具有一定的借鉴。

因此，为了快速实现不同产地不同药材的分类与鉴别，本文针对若干不同产地与种类中药材的红外光谱数据，基于多元散射校正（Multiplicative Scatter Correction, MSC）理论，以工程数据处理软件Matlab、Excel及Spss为分析工具，计算出不同产地药材的特征数据，并对其进行分类，以此确定出药材的不同产地。最后，并对分类结果进行了检验。

2 药材光谱数据分析

光谱[6]是指复色光在经过色散系统后，被色散后单色光按波长的大小而排列的图案。由于同一药材在不同的生长条件或者外部环境的影响下，对太阳光的吸光度表现出不同的特性。因此，可以利用近红外与中红外光谱的照射来鉴别药材的种类。而且对比问题中已知图1可知，药材A和药材B的波数趋势相差较大，药材A在波数1000的吸光度最高，达到了0.3（AU），而药材B在波数［1000，1500］区间的吸光度最高，只有0.16（AU）。其峰位相差较大，峰强趋势不一致，峰数出现次数也大不相同，对比可知不同种类的药材差异性较大。

利用数据分析软件Matlab对425组药材的红外光谱进行处理，结果如图1所示。

图1 425组 中药材数据曲线图

由图1可知，由于425组原数据未进行预处理，在[0，0.4]的数据存在大部分重叠，题中给出数据存在负值，且负值对其影响较小。图中横坐标表示光谱的波数，纵坐标表示吸收的中红外光，令起点区间［0.7，0.9］为第一组数据；起点区间［0.5，0.6］为第二组数据；起点区［0，0.4］为第三组数据。第一组数据的两条波数大体趋势较为相似，可判断其为同一种药材。同理可得，第二组数据为第二种药材，第三组数据为第三种药材。这三种波长的峰度和峰强有所不同，第一组数据的波数在［500，1000］之间峰位较高；第二组数据的波数在［1000，1500］之间峰位最高；第三组数据的波数在［500，1000］之间峰位最高，峰位越高，则峰强越强。

由于图1中数据众多，而且大部分数据曲线存在重叠与交叉现象，不利于数据的处理与分类。因此可以考虑将425组数据曲线进行分离，可以通过对数据曲线峰型进行对比，进而实现药材种类的鉴别与分类。425组中第221-330组数据曲线如图2所示。

图2 221-330组中药材数据曲线图

由图2可知，第（221、222、225、226、227...）组数据的波数在［0，1000］（cm-1)的峰位最高，峰数出现次数基本相同，且峰强大体趋势一致，可以判断其为同一种药材；第（234、258、279、297、309...）组数据的波数在［0，1000］（cm-1)的峰位最高，在［1000，4000］（cm-1)之间曲线峰数和峰强比例大体相同，则为另一种药材；第（223、230、233、236、239...）在［0，2000］（cm-1)之间的峰型走向以及峰位、峰强基本一致，且［2000，4000］（cm-1)之间图形基本吻合。但是，由于光谱图的相似度判定存在着一定的人为主观因素，对中药材的鉴别存在很大缺陷，且由于图1中下半区域出现严重重叠，导致无法研究药材的差异性和特征,因此基于现代的分析工具，寻求一种便捷快速的药材种类鉴别方法是现代中药材研究的必须。

多元散射校正[7]MSC是高光谱数据预处理常用的算法之一，它可以有效地消除由于散射水平不同带来的光谱差异，从而增强光谱与数据之间的相关性。因此，本文将基于MSC理论进行中药材鉴别模型的建立与求解，以达到中药材种类鉴别的目的。

3 基于MSC中药材鉴别模型建立

基于对上述中药材光谱数据的分析，首先通过下式来计算光谱数据中的平均光谱:

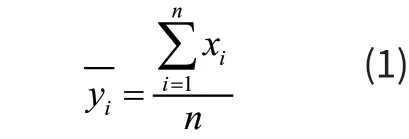
式中X表示n×p维（二维）定标光谱数据矩阵，n为定标样品数，Ai与平均光谱A进行一元线性回归后得到的相对偏移系数和平移量。一元线性回归式可以表示为：

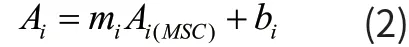
式中，矢量Ai是1×p维矩阵，表示单个样品光谱矢量，mi和bi分别表示各样品近红外光谱矢量。根据上式则多元散射校正可以表示为：

由于均值、中位数、众数、极差、标准差可以反映数据的特征、相似度及差异性。均值可描述每列数据取值的平均位置，如下式：

标准差是离均差平方的算术平均数的算术平方根，用σ表示：

极差是指其最大值与最小值之间的差距，xmax为最大值，xmin为最小值：

均方差表示，一个数据集的离散程度，记作s：

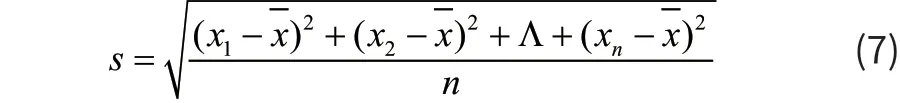
并对其进行求解，部分结果如表1所示。

表1 各个数据特征表

从表1中可以观察到，均值最高是0.843，最低为0.244，在［0.02，0.09］之间；中位数最高为0.0643，最低为0.0168，在［0.01，0.07］之间；众数最高为0.0216，最低为-0.0008，在［0.0001，0.03］；极差最高为0.3433，最低为0.0790，为［0.07，0.35］；标准差最高为0.822，最低为0.0195，在［0.01，0.9］，对此均值在0.04以下为一种药材，［0.04，0.07］为第二种药材，0.07以上为第三种药材。在上述确定药材种类中，选取数据较少，结果可能存在偶然性。多元散射校正可以放大数据的特征，因此经过对图1的MSC处理，得到研究性较高和观察性较明显的数据图3。

图3 多元散射校正后中药材数据曲线图

由图3可知，药材数据可以可分为三组，起点［0.3，0.7］中三条波数为第一组数据，即附件一中的数据64、136、201 ，起点［0.1，0.4］中的波数为第二组数据，起点［-0.1，0.05］中的波数为第三组数据。图中可以看出三组数据大致在［0，1500］之间的峰位较高。第一组数据在［0，1500］峰位较高，峰强趋势基本一致；第二组数据在［0，1000］的峰位较高，峰数与峰强基本相同；第三组数据在［400，1000］的峰位较高，且425组药材中红外光谱曲线峰型基本一致。

4 模型检验

为进一步验证上述模型的准确性，本次将利用数据挖掘[8]，及皮尔逊相关系数[9]来进行模型检验。在上文研究可得的三种药材的组数范围内分别挑选一组药材数据（64、139、202），第64组图4(a)数据中，区间[-2.06，1.73]在总体数据中占比最大；同理可得，第139组图4(b)数据在区间[-0.204，0.00203]占比重最大；第202组图4(c)数据在[-0.0108，0.099]占比最大。根据对图1中的425组数据分析可知，图1中红外光谱数据存在三种药材。

图4 三种药材任意一组数据贡献率图

表2(A)为NO与OP的皮尔逊相关系数表，(B)为NO与Classs的皮尔相关系数表。

表2 皮尔逊相关系数表

在正态分布显著标准图中，显著性数据小于等于0.001时为极性相关；在≥0.05，＜0.001为强性相关，显著数据≥0.1，＜ 0.05时为相关性，数据在＜ 0.1时可以确定两组数据为相关性数据。由表2(A)可知，显著性数据0.001及两组数据相同率为99.9%，由表2(B)可知，显著性数据为99.4%，由此可知，两组数据都在极性相关区间内，由此证明NO 、Class 、OP 产生于同一组数据。由此可以鉴定马氏分类法做出的药材产地与类别鉴定结果正确。

5 总结

本文基于多元散射校正理论对425种不同产地不同药材进行了鉴别与分类，并建立了多元散射校正模型和验证模型，利用大数据分析工具对药材光谱数据特征值进行分析，确定了药材的不同产地及种类。