喷嘴参数对风送式喷雾机雾滴射程的影响
2023-01-11龚曙光宋青卓刘黎明龚京忠贺运初
龚曙光, 宋青卓, 刘黎明, 龚京忠, 贺运初
(1.湘潭大学 机械工程学院,湖南 湘潭 411105; 2.湖南九九智能环保股份有限公司,湖南 长沙 410205)
风送式喷雾机通过风机产生的高速气流将大量雾滴抛射到作业区域完成作业,具有效率高、成本低、移动性强、覆盖范围广等优点,已被广泛应用于工业除尘、空气治理和农业喷洒等领域[1-2],同时风送式喷雾除尘技术也已成为露天矿山、火电厂和建筑工地等场所治理扬尘的重要措施之一[3-5]。
诸多学者及科研人员针对风送式喷雾机开展了相关研究,欧亚明等[6]利用农机试验对风送式喷雾机的雾滴射程进行了分析,研究结果表明轴流风机的性能对风送式喷雾机的雾滴射程影响较大,并指出雾滴被气流携带的最低风速为2 m/s,可作为喷雾机射程的判断指标;陈波等[7]基于多目标智能协同优化方法,探究了喷雾机关键结构参数对风机射程的影响规律,并得出最佳结构参数;张小涛[3]采用试验和数值模拟方法,研究了风量、喷雾压力与喷嘴角对雾滴扩散与沉降的分布规律的影响;宋淑然等[8-11]基于数值模拟方法和试验探究了喷雾机的喷雾特性、雾滴粒径变化规律,以及不同液体张力对喷雾机流场中雾滴的粒径、分布密度、速度和沉积分布情况的影响;李杰等[12]利用CFD法研究了喷雾机雾滴运动轨迹和沉降特性,所得结果与试验测试相吻合;刘秀娟等[13]采用Fluent软件分析了风机与射程范围内的气流信息及其轴向速度的衰减规律;EMMA等[14]建立了雾滴大小和雾滴速度的CFD模型,并对喷雾的分布规律和喷雾效果进行了评价;吕晓兰等[15]探讨了喷雾技术参数对雾滴沉积分布的影响;惠双琳[16]利用Fluent软件探讨了喷雾压力对降尘喷雾性的影响,指出喷雾压力越大、喷雾效果越好,雾滴的抗风能力越强。
已有文献对喷雾机射程的研究主要侧重于如何提升喷雾机的出口气流速度或重点针对雾滴的运动过程,而对雾滴的有效作用范围及喷嘴参数等对雾滴射程的影响还需进一步研究。因此,笔者基于雾滴运动、蒸发、碰撞和破碎方程,采用数值模拟和正交试验法,探讨喷嘴的结构与工艺参数对雾滴射程的影响,以期为风送式喷雾机的设计及工业应用提供参考。
1 控制方程及仿真模型
1.1 控制方程
1)湍流模型
连续相采用 Realizablek-ε湍流模型,该模型更适用于圆形射流[17],其动能方程如下:
(1)
扩散方程为:
(2)
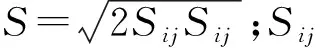
选取常数C1ε= 1.44,C2= 1.9,σk= 1.0,σε= 1.2。
2)雾滴运动方程
雾滴的运动轨迹可通过对拉格朗日坐标系下雾滴作用力的微分方程进行积分得出,雾滴作用力的平衡方程为:
(3)
式中:m为质量;τ为雾滴的弛豫时间;Fvm为雾滴所受的虚拟质量力;下标f为流体参数,未注下标的为雾滴参数。
3)雾滴碰撞方程
在雾滴的碰撞方程中,假定雾滴组之间的碰撞只存在于同一个流体网格内,此时可利用O′Rourke的随机方法来估计颗粒之间的碰撞频率,该计算方法在空间上具有二阶精度[18]。
2个雾滴组之间发生碰撞概率的数学期望为:
(4)
式中:r为雾滴组半径;vrel为2个雾滴组之间的相对速度;v为雾滴的总速度。
雾滴组实际碰撞次数的概率满足泊松分布,即:
(5)
如果雾滴之间为正面碰撞,则其结果倾向于雾滴合并;若为侧面碰撞,则其倾向于反弹。即雾滴之间碰撞会出现合并和反弹,判断其临界值为:
(6)
其中:
式中We为雾滴的韦伯数。
4)雾滴破碎模型
雾滴的破碎模型主要有TAB模型和WAVE模型,而后者的参数与工况环境相关[19]。为避免使用破碎模型带有的不确定性,本文采用TAB模型。
雾滴系统受迫有阻尼振动的控制方程为:
(7)
式中:F为雾滴的空气动力;d为阻尼力类比雾滴黏性力。
对于无阻尼雾滴,在其相对速度为0时,则有:
(8)
式中:ω为雾滴的振动频率;td为给定时间。
若y>1,则表示雾滴变形已增长到雾滴半径的临界值。雾滴破碎后,其尺寸分布的索太尔中径为:
(9)
式中:K为变形能量与一阶模态能量之比;σ为雾滴表面张力系数。
1.2 仿真模型
风送式喷雾机主要由风机、风筒、导叶、水泵、管路和喷嘴等组成,其中喷嘴在出口处均匀环绕,其分布如图1所示。
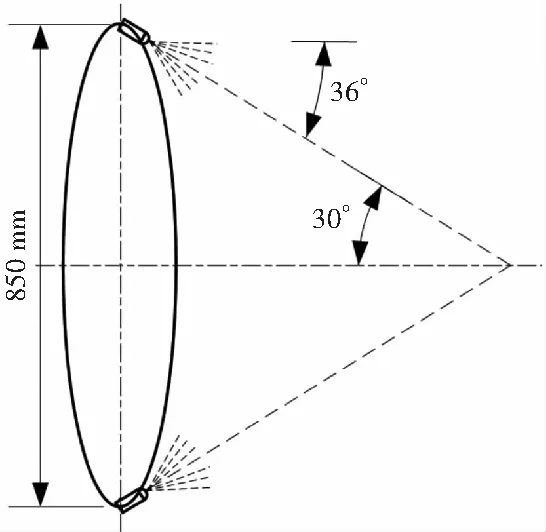
图1 喷嘴分布示意图
选取的喷雾机喷嘴直径为850 mm,喷嘴数量为80个,各喷嘴轴心与风筒轴心的夹角为30°;选定喷嘴类型为压力旋流型喷嘴,其孔径为0.75 mm;水泵压力为2.5 MPa,喷雾半锥角为36°。
根据风送式喷雾机风筒出口尺寸及额定射程距离,建立六面体流域,流域的结构尺寸参数如图2所示。
图2 风送式喷雾机流域示意图
风筒出口中心距离地面高度为1.5 m,风筒出口轴线与水平地面的夹角为20°。
由于流域较为规整,采用六面体结构网格对其进行网格划分,并对入口区域采用O型切割并进行加密处理。
1.3 边界条件及计算
边界条件:将喷雾机风筒出口设为速度边界,其值为36 m/s,温度293 K,相对湿度50%;地面采用无滑移壁面边界,近壁区为标准壁面函数,DPM边界采用TRAP;其他边界为压力边界,其值为标准大气压,DPM边界为Escape。
采用压力旋流雾化喷嘴注入雾滴,流量设为0.2 kg/s,并在仿真计算中开启TAB雾滴破碎模型。同时考虑重力的影响,重力加速度为9.8 m/s2。
计算状态设置为瞬态,取时间步长为0.01 s,每个时间步长最大迭代次数设为40次,计算时长设置为20 s。数值计算采用压力—速度耦合求解算法,压力方程采用二阶迎风格式求解,压力—速度耦合采用SIMPLEC算法。
1.4 网格无关性及验证
通过对所建网格进行细化,并取x=80 m的平均速度作为网格无关性验证的指标,所得到的计算结果见表1。
表1 网格无关性验证
由表1可知,当流域的网格数从212.5万增加到430.1万个时,平均风速逐步趋于稳定。为了减少计算量,最终选取流域的网格数359.2万个。
为了验证喷嘴雾化模型的可行性,在相同工况下,对喷嘴模型进行仿真分析,计算得到的雾滴粒径分布曲线与试验测试结果的对比如图3所示。
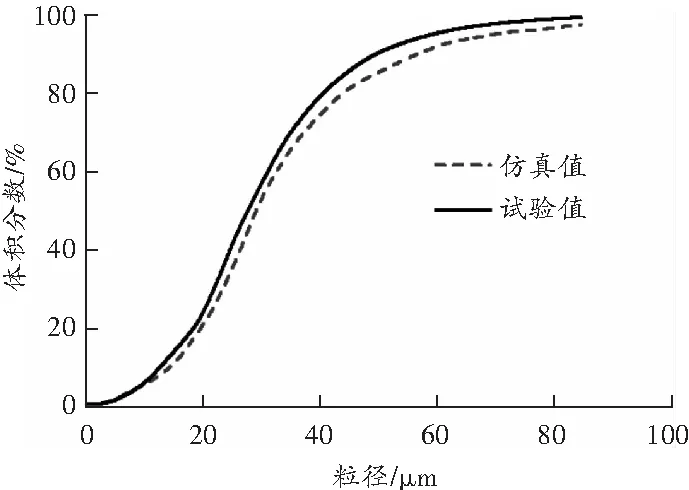
图3 喷嘴雾化的结果对比
由图3可知,喷嘴雾化模型所得到的雾滴粒径分布与试验测试值具有相同的变化规律,二者的数值也较为接近,说明所建立的喷嘴雾化模型是可行的。
2 结果分析与讨论
通过对所建的仿真模型进行计算,得到有雾滴与无雾滴时气体流场的速度云图,如图4所示。
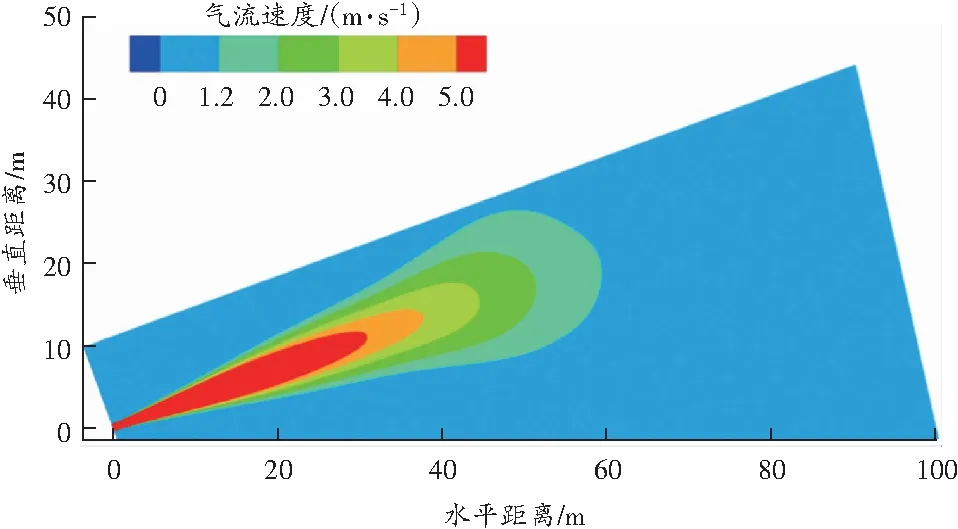
(a)无雾滴
从图4(a)可以看出,无雾滴时,气体流场的速度分布呈现锥形对称分布,且随着出口轴线距离的延长,气体的流速逐渐减小,这与气体自由喷射模型的流场特征相吻合。
从图4(b)可以看出,当气体中含有雾滴时,由于雾滴颗粒耦合诱导作用,使气体流场末端速度分布形态比无雾滴时要大,且向地面弯曲,这主要是因为随着气体流速的减小,雾滴在其重力作用下发生沉降,以及微小雾滴在气流作用下发生扩散漂移所引起,且雾滴沉降是主要的诱因。
雾滴颗粒粒径及其轨迹的分布如图5所示。
图5 雾滴颗粒粒径及其轨迹的分布
由图5可知,雾滴的分布形态呈现抛物状,在其前3/5的距离,由于受到高速气流的裹挟作用,雾滴分布相对集中即处于喷射阶段;随着气流速度的减小,粒径大的雾滴首先开始沉降,当气流速度减小到不足以支撑雾滴时,雾滴在惯性下呈现抛物沉降运动并靠近地面,此段位于3/5~4/5处;当雾滴靠近地面后,由于其沉降阻力增大,雾滴会沿着地面漂移。即雾滴经历喷射、沉降和漂移的距离之比接近3∶1∶1。
在雾滴沉降到地面后,每平方厘米内雾滴的个数即雾滴密度与距离之间的关系如图6所示。
图6 雾滴密度随距离的分布规律
从图6可以看出,落到地面上的雾滴密度随距离的增加呈现先增大后减小的趋势,其有效作用范围为60~78 m,即为最大射程的77%~100%。按照国家机械行业标准[20],将地面处每平方厘米内雾滴颗粒数达到10个的最大水平距离作为喷雾机的射程,分析图6得到所建模型的最大喷雾射程为78 m,雾滴密度的最大值出现在69 m处。
3 正交试验分析
根据风送式喷雾机的结构特点和工艺参数,取喷嘴的分布直径、喷嘴数量、喷嘴角度、工作压力及喷嘴孔径作为影响因素,其正交试验因素值如表2所示。
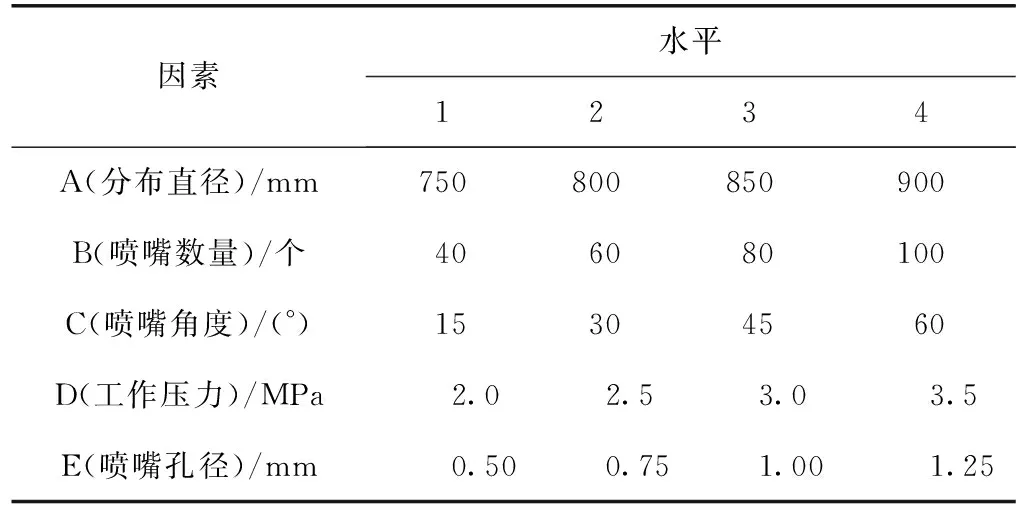
表2 因素水平
正交试验采用标准的L16(45)正交试验表,正交试验结果和极差分析如表3所示。
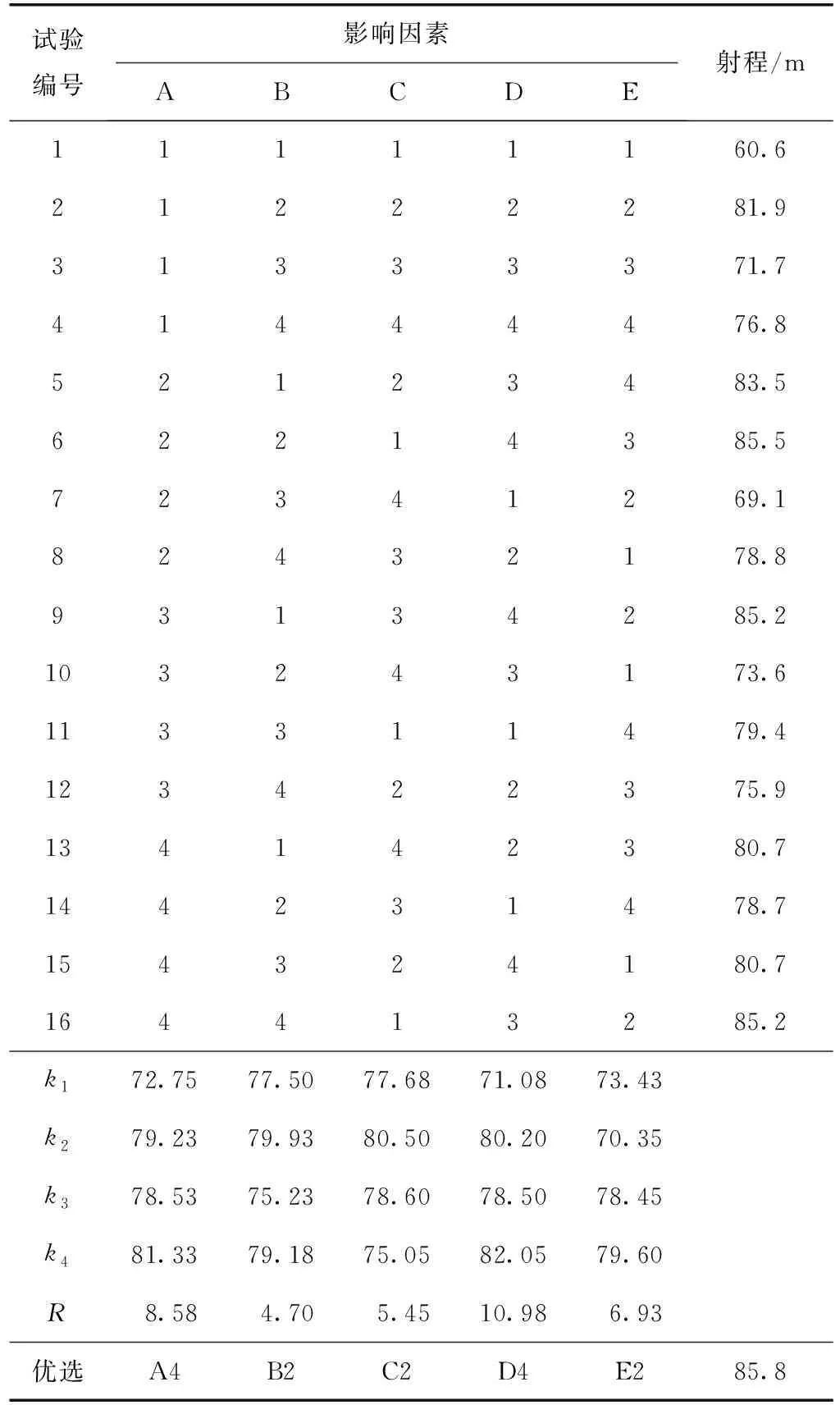
表3 正交试验结果和极差分析
由表3可知,获得雾滴最大射程的因素组合为D4A4E2C2B2,影响雾滴射程因素的主次关系为:工作压力、分布直径、喷嘴孔径、喷嘴角度、喷嘴数量。分析表明要增大喷雾机的射程,可适当增大喷嘴的工作压力和分布直径,减少喷嘴数量。
采用最佳组合方案后,沉降到地面上每平方厘米内的雾滴数量分布如图7所示。
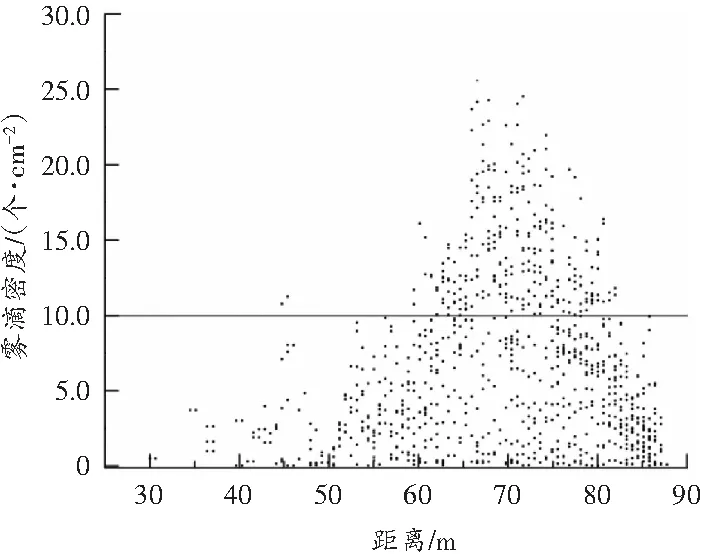
图7 最佳方案地面雾滴密度情况
从图7可以看出,喷雾机的有效作用范围为55.0~85.8 m,雾滴的最大射程为85.8 m。同时对比图6可知,有效作用范围增大了167%,最大射程提升了6.4%,落入地面的雾滴密度分布更加集中,这更有利于扬尘的治理。
4 结论
1) 喷雾机的雾滴运动经历了喷射、沉降和漂移3个阶段,且其距离之比接近3∶1∶1。喷射阶段决定了雾滴射程的大小,雾滴的有效作用范围为最大射程的77%~100%。
2) 影响雾滴射程因素的主次关系为:工作压力、分布直径、喷嘴孔径、喷嘴角度、喷嘴数量。
3) 采用最佳组合方案后,不仅增大了喷雾机有效工作范围,提升了最大射程,而且落入地面的雾滴密度分布更加集中,从而更有利于扬尘治理。
