地电阻率交流观测中的电感性耦合效应特征模拟和分析
2023-01-10马小溪王兰炜朱涛张宇张兴国
马小溪, 王兰炜, 朱涛, 张宇, 张兴国
1 中国地震局地球物理研究所, 北京 100081 2 吉林省地震局, 长春 130117 3 中国地震局地震预测研究所, 北京 100036
0 引言
地电阻率法是观测视电阻率随时间变化的一种地震预报手段.经过几十年的发展,其观测技术和预报方法日趋成熟和完善,在地震监测预报研究中发挥了重要作用.在台网监测范围内,多次记录到中强地震前的地电阻率趋势异常变化(赵玉林和钱复业,1978;金安忠,1982;钱复业和赵丰林,1982;钱复业等, 1990;赵和云和杨明芝,1984;赵家骝等,1996,2001;钱家栋和曹爱民,1998;钱家栋等,2013,2018;张学民等,2009;朱涛,2013;Lu et al.,2016;王立凤等,2017;叶青等,2017;王同利等,2020).尽管研究取得了很大的发展,但地震预报目前仍是尚未解决的世界性科学难题.地震预报研究需要根据长期实践积累的大量观测数据和震例资料,总结出经验性规律并推广应用于预测未来地震(张国民等,2001).因此,保证观测资料的质量和连续性是地震预报研究的重要基础.
目前我国地电阻率观测多采用单一极距的直流供电观测方法(钱家栋,2010).随着我国经济社会的高速发展,地电阻率观测越来越多地受到测区内杂散电流的干扰,特别是近直流频段的地铁、轻轨等城市轨道交通的干扰,其干扰范围可达数十千米(谢凡等,2011;张世中等,2013).城市轨道交通干扰信号的周期主要在120~180 s(马小溪等,2015;张宇等,2016).干扰造成地电阻率观测值呈现大幅度、高频次的突跳变化,测量方差明显变大,从而导致台站观测数据不符合地震监测预测研究的要求,一些台站甚至被迫搬迁,严重影响地震预报观测资料的积累.
为了解决地电阻率观测中的干扰问题,近年来,国内外专家主要从观测数据处理和观测方法改进两个方面开展了研究.汪凯翔等(2020)对长短时记忆神经网络进行训练,并应用于地电场数据处理研究中,Wu等(2021)将长短时记忆网络与自动编码器结合,开发了新型神经网络结构,以抑制瞬变电磁信号噪声,为地电阻率观测数据干扰处理提供了一定的参考.李伟等(2007)、李鸿宇等(2016)采用夜间数据均值(非地铁运营时段)代替日均值进行数据分析,运用均方差法选取合适的时段数据,能够获得观测精度较高的观测值.但是,该方法对观测数据使用率较低,多数台站每天仅有4~5 h数据可用.王燚坤等(2019)运用小波包阈值方法对合肥台原始观测数据进行分析和重构,认为该方法能够较好地滤除地铁干扰噪声,保留原始信号.但是在距离地铁较近的台站,该方法的去噪效果不理想.当干扰幅度过大,造成仪器超量程时,会造成错误的观测结果,数据处理的方法就无效了,因而需要寻求观测方法的改进.
新的观测方法是从根本上解决干扰问题的有效途径,地电阻率交流观测方法能够有效抑制杂散电流的干扰,特别是城市轨道交通(地铁、轻轨等)的干扰.在20世纪80年代,桂燮泰等(1988)、马希融(1989)曾在河北马家沟开展了为期4年的低频交流电法的观测试验.其观测结果表明,交、直流观测结果的变化趋势基本一致,交流观测能够更好地抑制工业游散电流的干扰.张宇等(2016)研发了专门用于地震电阻率观测的新型地电阻率交流观测系统,并在受地铁干扰严重的江宁台开展了观测试验.试验结果也表明交流供电的地电阻率观测方法能够很好地抑制城市地铁、轻轨等引起的干扰,但不同频率的交流观测值之间存在差异,且与直流观测结果存在差别(王兰炜等,2019).
造成地电阻率交流观测结果随供电频率变化的原因可能有以下三种:(1)交变电流场中的岩、矿石激电效应;(2)不同频率的交变电流的趋肤深度不同;(3)采用交流信号供电,供电线路中电流的变化在测量线路中产生的电感性耦合效应.
交变电流场中的岩、矿石激电效应主要表现为当用一对供电电极向岩、矿石供以固定大小的低频交变电流,并用另一对电极测量电位差时,测量到的电位差会随频率的增高而逐渐降低,而且电位差的相位相对于电流的相位有一定的滞后,同时,频率越低,电位差及交流地电阻率观测值越高(程志平,2007).地电阻率交流观测值的特征为随频率增大而增大,与激电效应的表现特征不一致,因此激电效应不是造成地电阻率交流观测结果随供电频率变化的原因.
低频交流电法的趋肤深度随供电信号频率的减小而增大.对于水平层状介质模型,地电阻率法观测的视电阻率值为探测范围内各层电阻率值的综合体现(钱家栋,2010).如果观测场地的电性结构为上层高阻、下层低阻,随供电信号频率的减小,探测深度逐渐增大,受下层低阻的影响,地电阻率交流观测值减小;反之,如果观测场地的电性结构为上层低阻、下层高阻,随供电信号频率的减小,地电阻率交流观测值增大.选择地下电性结构不同的三个台站进行地电阻率交流观测试验,嘉峪关台“KH”型(ρ1<ρ2>ρ3<ρ4)、四零四台“H”型(ρ1>ρ2<ρ3)、乌加河台“K”型(ρ1<ρ2>ρ3),试验结果显示地电阻率交流观测值均随供电信号频率增大而增大(详见第3节),由此可见,不同供电信号的趋肤深度对地电阻率交流观测结果的影响较小.
通过在实验室使用长导线(200 m)模拟平行布设的供电线与测量线进行电感性耦合效应模拟试验,用不同供电频率信号模拟地电阻率交流观测,实验结果与台站实际观测结果的变化规律一致,表现为随供电频率增大而增大,电压测量值的相位超前于电流测量值的相位,相位差为正值.证实电感性耦合效应在地电阻率交流观测过程中确实存在且影响较大.
综上所述,相比于岩、矿石的激电效应和不同供电频率的趋肤深度的影响,电感性耦合效应是影响地电阻率交流观测结果的主要因素.
对于地震监测来说,地电阻率方法更关注观测值随时间的长期相对变化,固定的装置系统和确定的供电频率所造成的电感性耦合影响是确定的,且不会影响地电阻率长期的趋势性变化.因此不同供电频率之间的地电阻率观测值的差异并不会影响到观测数据的使用,但是探究其产生的原因并将其消除,对于进一步推动该方法的发展具有积极的意义.
为此,本文建立了地电阻率交流观测的电感性耦合模型,通过正演模拟分析电感性耦合随供电信号频率、地电阻率值、以及供电线和测量线之间的距离、平行长度等参数的变化规律,总结地电阻率交流观测装置布设所需要考虑的影响因素;然后使用该模型对试验台站的观测值进行预测,通过对比分析相同试验参数下的模型预测值与台站实测值,验证模型的有效性,使电感性模型能够有效反映台站地电阻率交流观测的实际情况,为地电阻率交流观测方法的推广应用提供理论参考.
1 模型建立方法
1.1 地电阻率的计算
在地震电磁学中,地电阻率的测量方法源自于物探电法中的地电阻率测量方法,原则上可采用任意形式的电极排列,即在地表任意两点用供电电极A、B供电,而在另两点用测量电极M、N测定电位差.在我国地电阻率台站的观测中,大部分采用的是对称四极观测装置(图1),其两个供电极A、B和两个测量极M、N排列在同一条直线上(钱家栋,2010;中国地震局,2010).外线路采用架空或地埋方式,供电线与测量线平行布设.在测量时,通过供电电极向地下供入一定强度的电流IAB,当电流达到稳定值时,在测区介质中将建立一个稳定的附加人工电场,测量这个稳定电场在测量电极之间的电位差UMN(图2),便可根据公式(1)计算观测区域的地电阻率ρs.
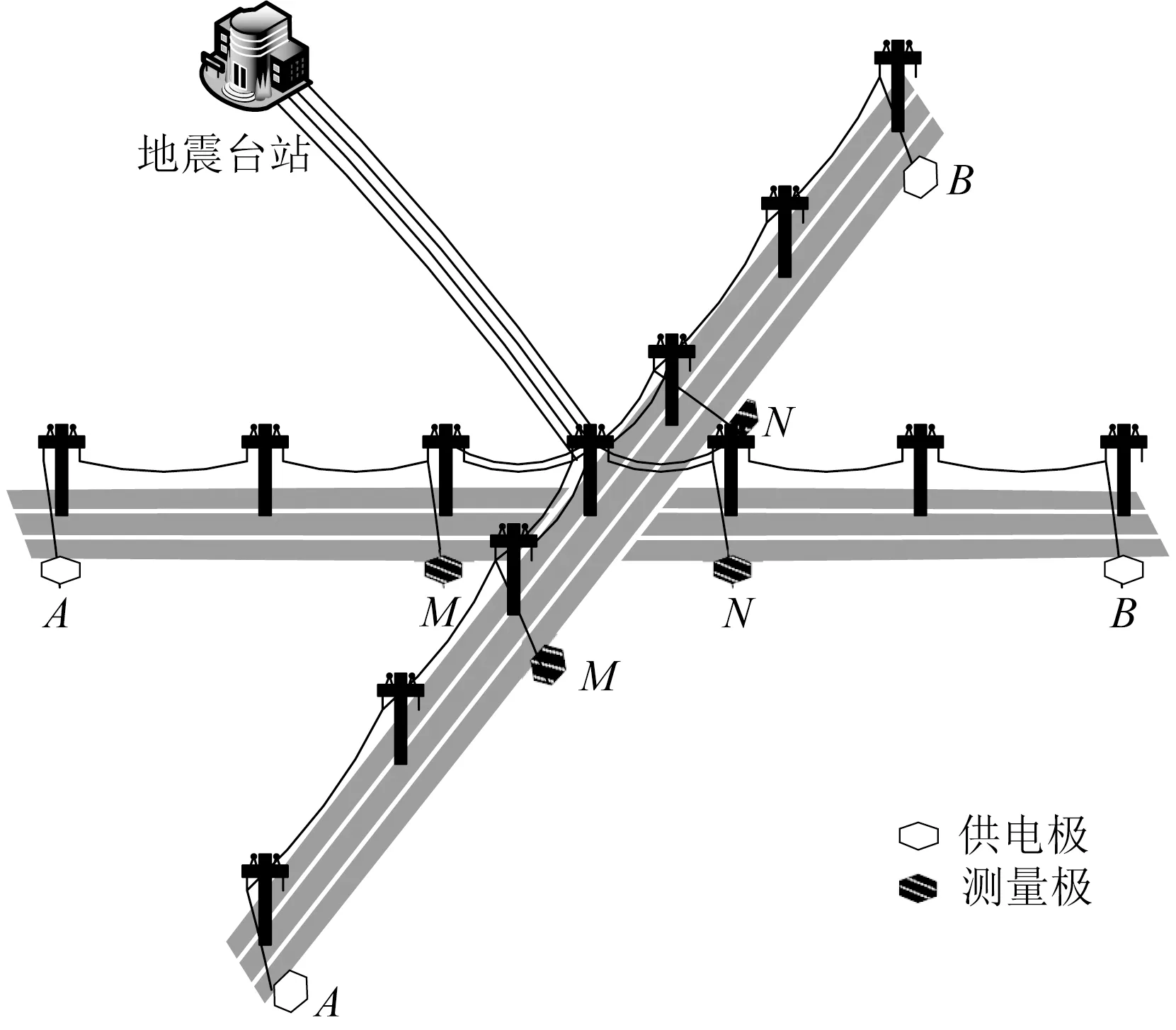
图1 地电阻率对称四极观测装置系统(架空)
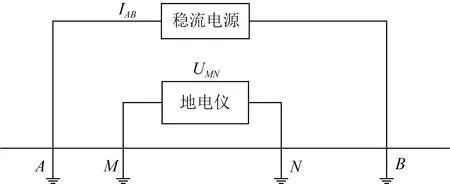
图2 地电阻率测量示意图
(1)
其中,K为装置系数.四极装置系统的装置系数由公式
(2)
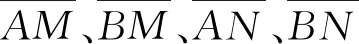
1.2 水平线间互感系数的计算
电感性耦合效应是由于两电路间的磁场相互作用所引起的.当一个电路中的电流I发生改变,其周围的磁场也会同时发生变化,从而产生电磁波,这些电磁波能够耦合到附近的电路中并且产生感应电动势(刘培国和侯冬云,2008;杨显清等,2016).在地电阻率交流观测中,供电线路中的交变电流信号除了在大地介质内部建立一个附加的似稳电场外,还在供电线周围产生电磁场,并通过电感性耦合效应在测量线路中产生感应电动势εEMI.使测量结果中既包含了测量电极M、N之间的人工电位差,又叠加了测量线路中的感应电动势,从而对观测结果造成影响.
因此,要计算受电感性耦合效应影响的交流地电阻率值(以下简称“耦合电阻率”),首先需要计算出感应电动势,而要计算感应电动势,则需首先计算线路的互感系数Mc(单位:H·m-1).依照国际电报电话咨询委员会(CCITT)导则第VII章附表中推荐的计算公式,当x<0.1时,平行接近段互感系数的计算公式如下(吕勤,1981;张文亮等,2013):
(3)
(4)
其中μ0=4π×107H·m-1,为真空磁导率;ω=2πf,为角频率;f为供电信号频率(单位:Hz);ρs为地电阻率(单位:Ωm);D为导线间距离(单位:m).
1.3 电感性耦合模型
受电感性耦合效应影响的地电阻率交流观测方法的等效电路模型如图3所示,地电仪测量的电位差ΔU由两部分组成,大地介质内部的稳定电场在测量极MN之间产生的电位差UMN以及由于供电线上交变电流变化在测量线上产生的感应电动势εEMI:
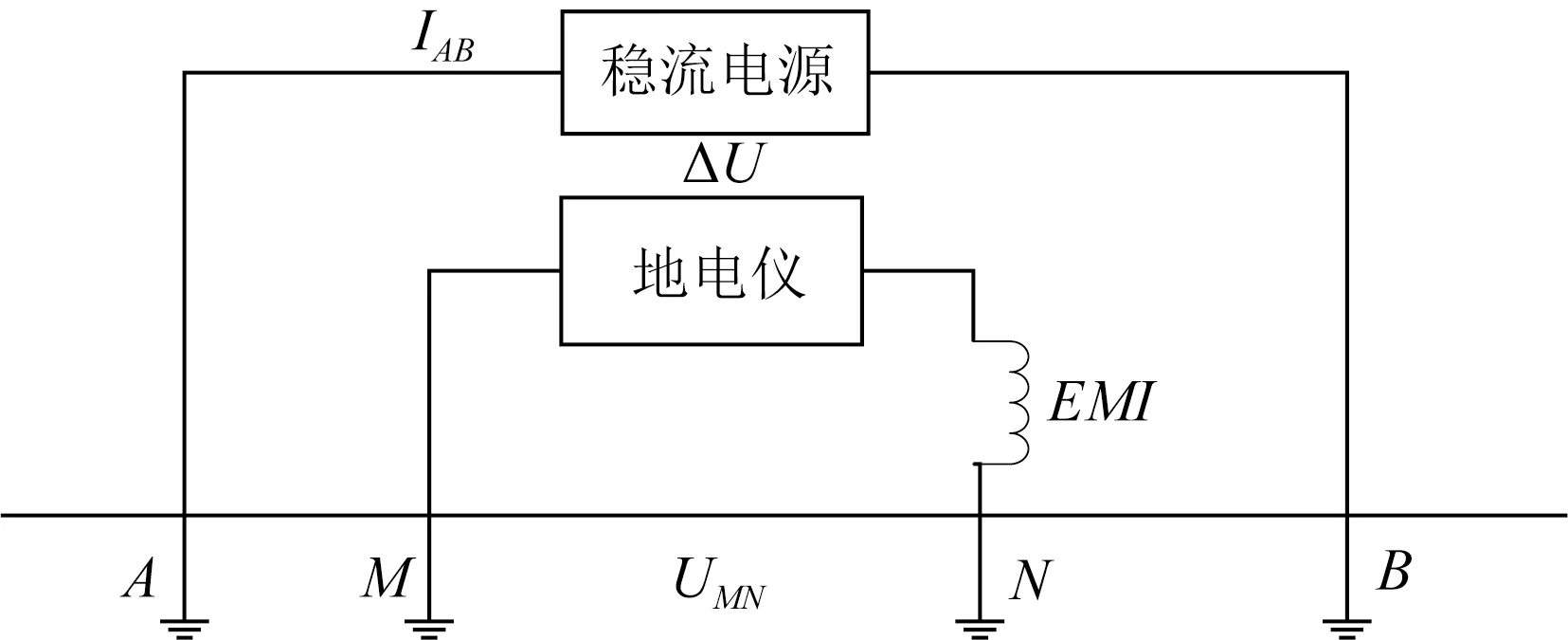
图3 电感性耦合效应等效电路模型
ΔU=UMN+εEMI,
(5)
由公式(1)可得,耦合电阻率的测量结果为
(6)
根据法拉第电磁感应定律,感应电动势εEMI=jωMcLIAB,代入公式(6)可得:
ρsEMI=ρs+jKωMcL,
(7)
其中L为供电线与测量线间平行长度(单位:m).
将公式(3)代入到公式(7)中,得到耦合电阻率的计算公式:
(8)
2 模型参数的正演模拟及分析
由公式(8)可知,耦合电阻率值与交流供电信号频率、地电阻率值、供电线与测量线间距离、供电线与测量线间平行长度、装置系数等参数相关.其中线间距离仅影响耦合电阻率的虚部,其他参数对耦合电阻率的实部和虚部均产生影响.此外,在四极观测装置中,平行长度即为测量极距,其与装置系数是相互影响的.考虑多数地电阻率观测台站的实际情况,正演模拟时假设装置系统为对称四极装置,供电极距1000 m,测量极距300 m,计算装置系数K=2381 m,线间平行长度L=300 m.设定交流供电信号频率为0.1~10 Hz,地电阻率值一般小于1000 Ωm,供电线与测量线间距离范围0.01~1 m.根据电感性耦合模型(公式8)计算耦合电阻率值,耦合电阻率与地电阻率的误差值(|ρsEMI|-ρs)能够反映电感性耦合效应的影响.下面分别讨论该误差值与供电信号频率、地电阻率值、以及供电线与测量线间距离三个参数的关系.
从图4可以看出,在设定的参数范围内,当供电频率和地电阻率值固定时,线间距离越大误差值越小,即电感性耦合效应的影响越小.例如在图4b中,供电频率为1 Hz,地电阻率为10 Ωm(黑色实线),当线间距离为0.01 m时,误差为5.34 Ωm;当线间距离为0.1 m时,误差为3.94 Ωm;当线间距离为1 m时,误差为2.71 Ωm.其整体的变化趋势近似于对数变化.
当测量区域地电阻率值不同时,线间距离的影响效果是不同的.例如在图4c中,供电频率为5 Hz,当地电阻率为10 Ωm时(黑色实线),线间距离从0.01 m增大到1 m所对应的误差值范围为43.11~23.53 Ωm;当地电阻率为50 Ωm时(红色实线),线间距离从0.01 m增大到1 m所对应的误差值范围为26.72~13.57 Ωm;当地电阻率为100 Ωm时(蓝色实线),线间距离从0.01 m增大到1 m所对应的误差值范围为17.95~9.56 Ωm;当地电阻率为250 Ωm时(绿色实线),线间距离从0.01 m增大到1 m所对应的误差值范围为10.20~6.34 Ωm.说明地电阻率值越大,线间距离的增大对应的地电阻率误差范围越小,此时单独增大线间距离将不能够明显改善电感性耦合效应的影响.此外,通过图4a—d的对比可以观察到,当地电阻率范围在10~250 Ωm、线间距离在0.01~1 m之间、供电频率分别为0.1 Hz、1 Hz、5 Hz和10 Hz时,对应的误差范围分别为0.07~0.14 Ωm、0.84~5.34 Ωm、6.34~43.11 Ωm和17.13~91.05 Ωm,误差范围随供电频率增大而增大,具体变化趋势如图5所示.
图5结果显示,在设定的参数范围内,当线间距离和地电阻率值固定时,耦合电阻率值与地电阻率的误差值随供电频率单调递增,供电频率越大,电感性耦合效应的影响越显著.例如在图5a中,当线间距离为0.1 m、地电阻率为10 Ωm时(红色实线),0.1 Hz频率的供电信号,误差为0.09 Ωm;1 Hz频率的供电信号,误差为2.04 Ωm;10 Hz频率的供电信号,误差为71.10 Ωm.同时,从图5a—d也可以看出,增加线间距离将减小误差值,这一结论与图4所示结果一致.
当单独考察地电阻率的影响时,误差值呈较明显的非线性变化特征.如图6所示,在设定的参数范围内,供电频率为0.1 Hz(黑色实线)和1 Hz(红色实线)时,受电感性耦合效应影响较小,地电阻率为10 Ωm,当线间距离为0.01 m时(图6a),0.1 Hz信号的误差为0.14 Ωm,1 Hz信号时的误差为5.34 Ωm;线间距离为0.1 m时(图6b),0.1 Hz信号的误差为0.12 Ωm,1 Hz信号的误差为3.94 Ωm;线间距离为0.5 m时(图6c),0.1 Hz信号的误差为0.11 Ωm,1 Hz信号的误差为3.06 Ωm;线间距离为1 m时(图6d),0.1 Hz信号的误差为0.10 Ωm,1 Hz信号的误差为2.71 Ωm.这进一步说明线间距离增大,地电阻率误差值减小,同时误差值范围相应缩小,这一结论与图4和图5数据一致.
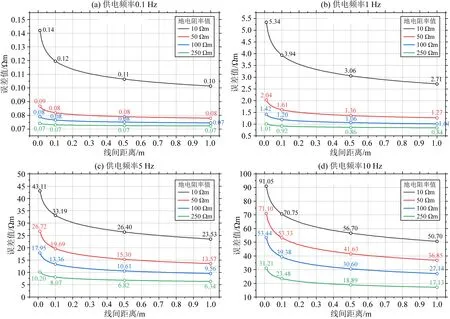
图4 电阻率误差值随线间距离的变化曲线
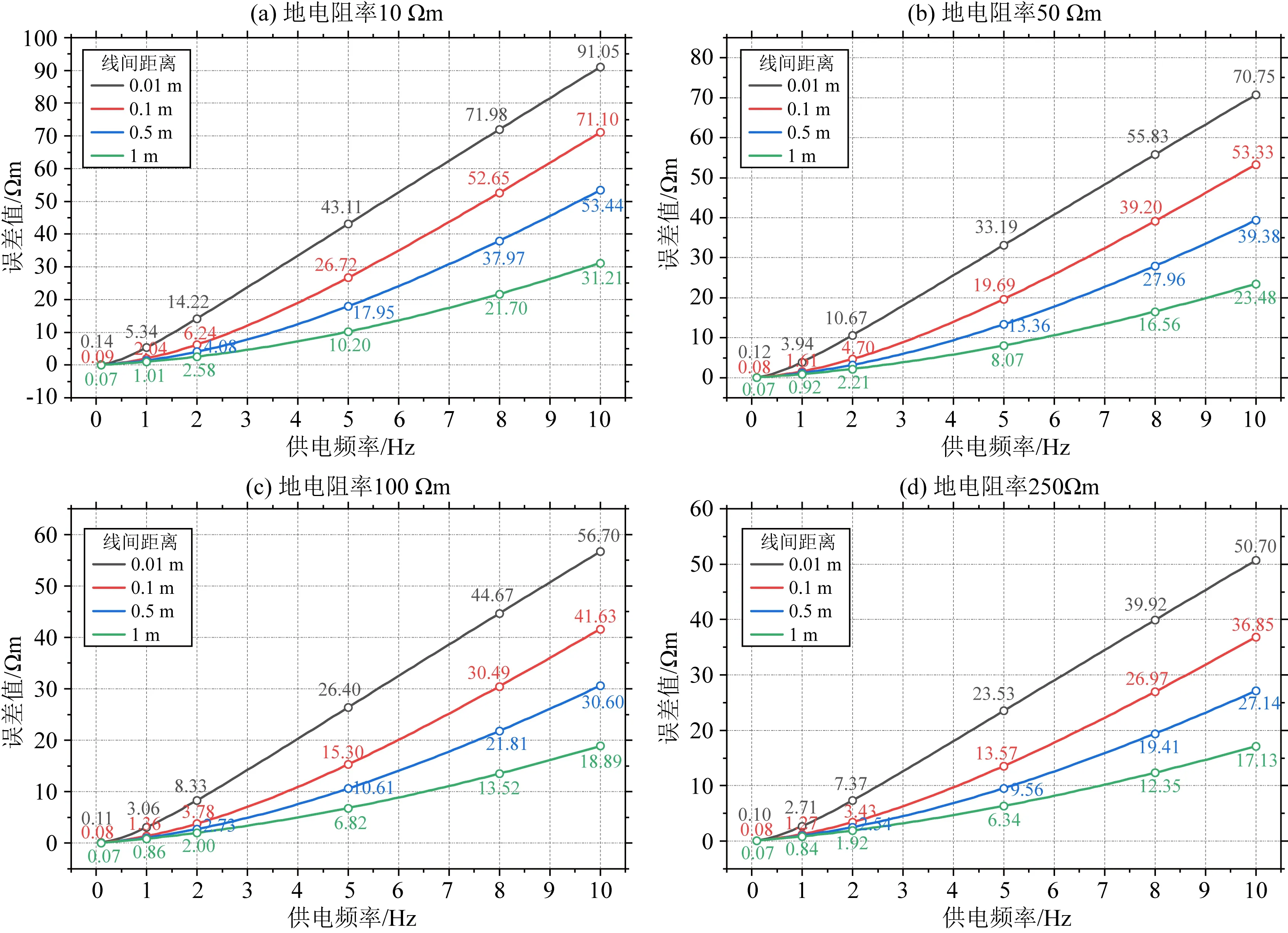
图5 电阻率误差值随供电频率的变化曲线
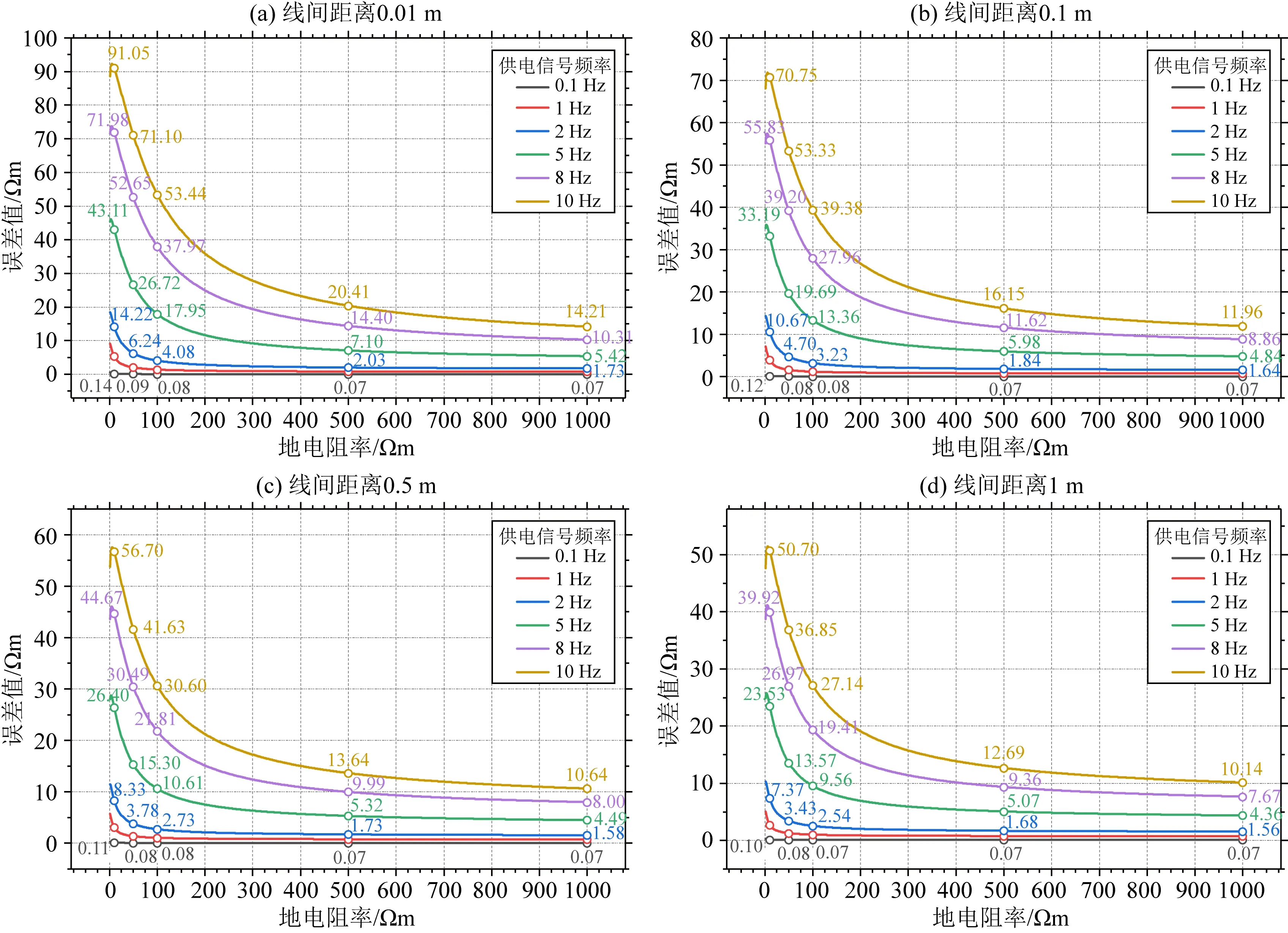
图6 电阻率误差值随地电阻率值的变化曲线
当供电频率在5~10 Hz范围内,在线间距离不变的前提下,随着地电阻率值的逐渐增大,耦合电阻率与地电阻率间的误差值先增大后减小,即电感性耦合效应的影响先变大再变小.对公式(8)中的ρs进行求导分析可得:
(9)
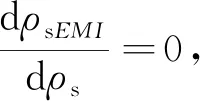
综上所述,想要减小电感性耦合效应的影响,需要综合考虑观测台站的地电阻率、电性结构、拟采用的供电信号频率和供电线测量线间的敷设距离等参数的影响.在实际台站装置条件的参数范围内,理论上应当适当增加线间距离,减小供电频率.需要注意的是,文中的数值模拟并没有考虑观测装置系统的不同对结果造成的影响,实际上,观测装置的线间平行长度(即测量极距)和装置系数也将对电感性耦合效应产生影响.根据公式(8),电感性耦合效应与装置系数和线间平行长度呈正比.但是根据公式(2),供电极距固定时,线间平行长度与装置系数呈反比.因此,如果考虑观测装置的线间平行长度和装置系数对电感性耦合效应的影响,那么产生影响的参数更多,数据的变化也更加复杂.
从正演分析结果可知,当地电阻率为10 Ωm,采用低于0.1 Hz频率信号供电时,耦合影响造成的观测误差小于0.14 Ωm,相对误差小于1.4%;当采用低于1 Hz频率信号供电时,当地电阻率大于100 Ωm,线间距离大于1 m时,耦合影响造成的观测误差小于1.01 Ωm,相对误差小于1.01%.这将为地电阻率交流观测装置系统的建设或改造提供基本的理论依据.
3 电感性耦合效应模型应用与分析
正演分析结果表明影响电感性耦合效应的参数包括交流供电信号频率、供电线与测量线间距离、供电线与测量线间平行长度和地电阻率值.为了验证电感性耦合模型的正确性,使用该模型对几个台站的地电阻率交流观测结果进行计算,模型参数选择地电阻率交流观测系统观测时的参数,计算得到模型预测结果,并与台站观测结果进行对比.试验台站的装置系统在观测过程中不会发生变化,因此供电线与测量线间距离、平行长度和地电阻率值是固定且已知的,通过调整供电信号频率,能够得到试验台站不同供电频率的模型预测结果ρpre,f和实际观测结果ρob,f,计算二者的误差值,
error(f)=|ρpre,f-ρob,f|,
(10)
通过对不同供电频率的误差值进行统计分析,可以验证电感性耦合模型的正确性和有效性,判断电感性耦合模型是否能够有效反映试验台站的实际观测环境.本文以嘉峪关地震台、四零四地震台、乌加河地震台、青光地震台等四个台站的8个测向的实际情况为例,采用电感性耦合效应模型计算台站耦合电阻率值,并与实际观测结果进行对比.其中地电阻率值由直流电阻率观测值确定,其他参数根据台站的实际情况设定(表1).通过电感应耦合模型计算不同供电频率时耦合电阻率值(图7—10星号),可以得到试验台站模型预测值与实际观测值的误差曲线(图7—10).图中横坐标为地电阻率交流观测系统在各试验台站测量的耦合电阻率值,纵坐标为电感性耦合模型的预测值,从左到右不同的星号对应的供电频率分别为0.1 Hz、0.5 Hz以及1~10 Hz,黑色虚线代表预测值与实测值相等的理想曲线,星号与黑色虚线的纵向距离即为预测值和实测值的误差值(公式10),误差值与实测值的比值为相对误差(公式11),各台站不同供电频率时的误差值的统计分析结果见表2.
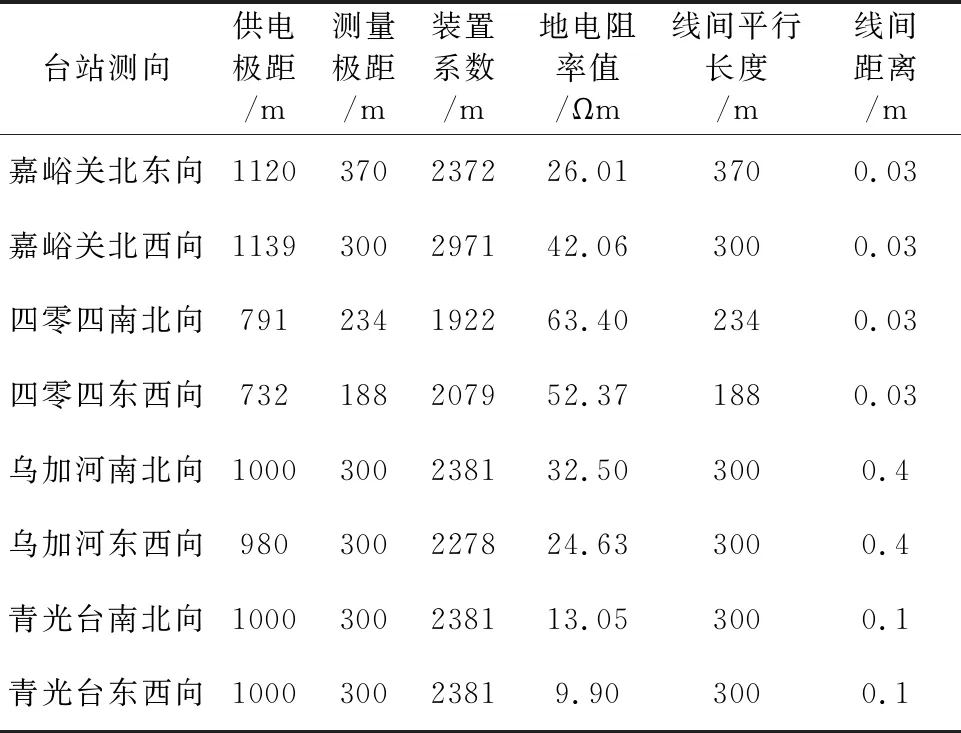
表1 试验台站装置系统参数
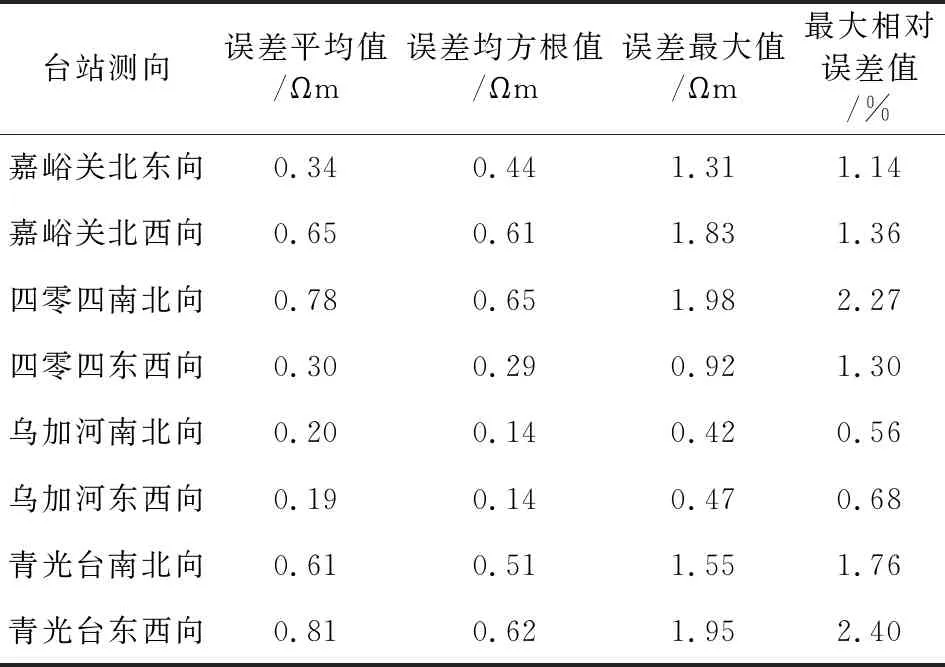
表2 地电阻率模型预测结果与交流实测结果的误差统计分析
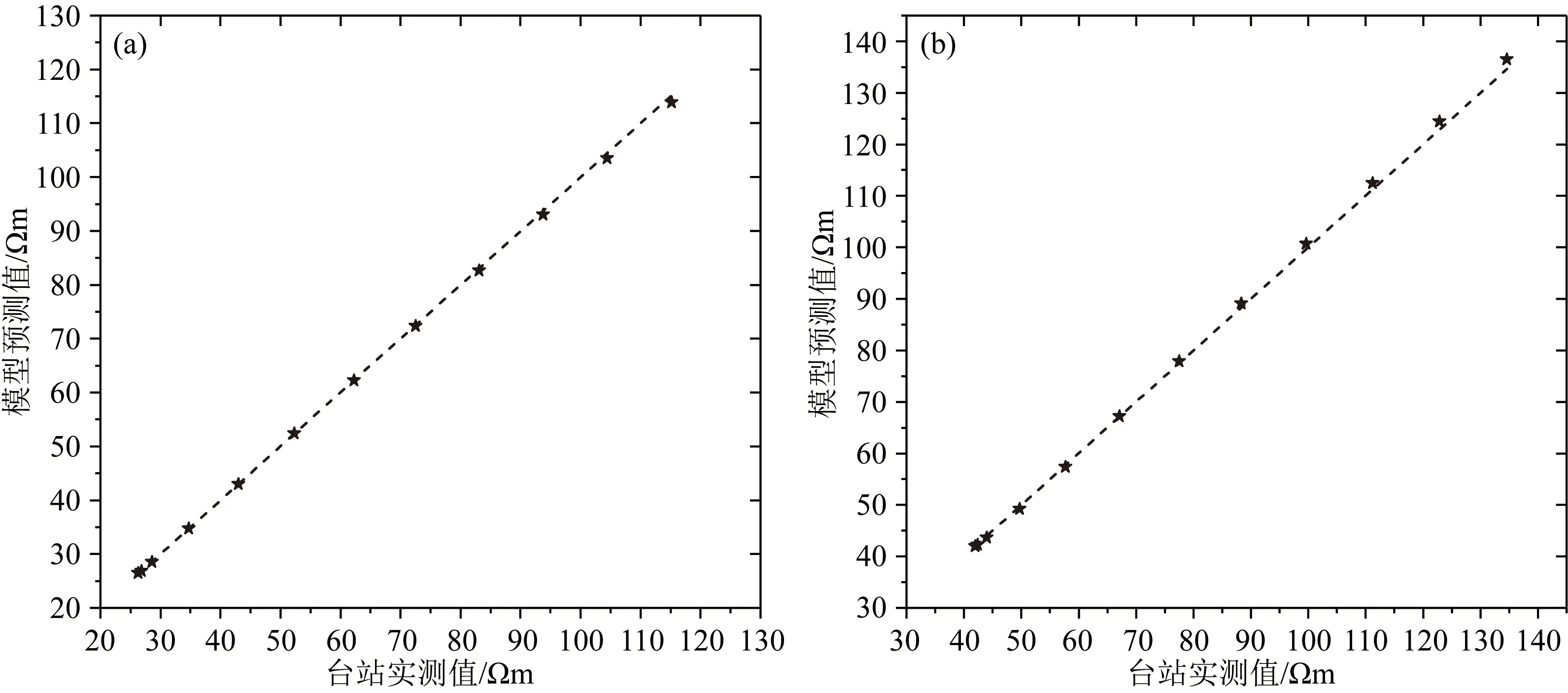
图7 嘉峪关地震台地电阻率模型预测值与台站实测值对比
(11)
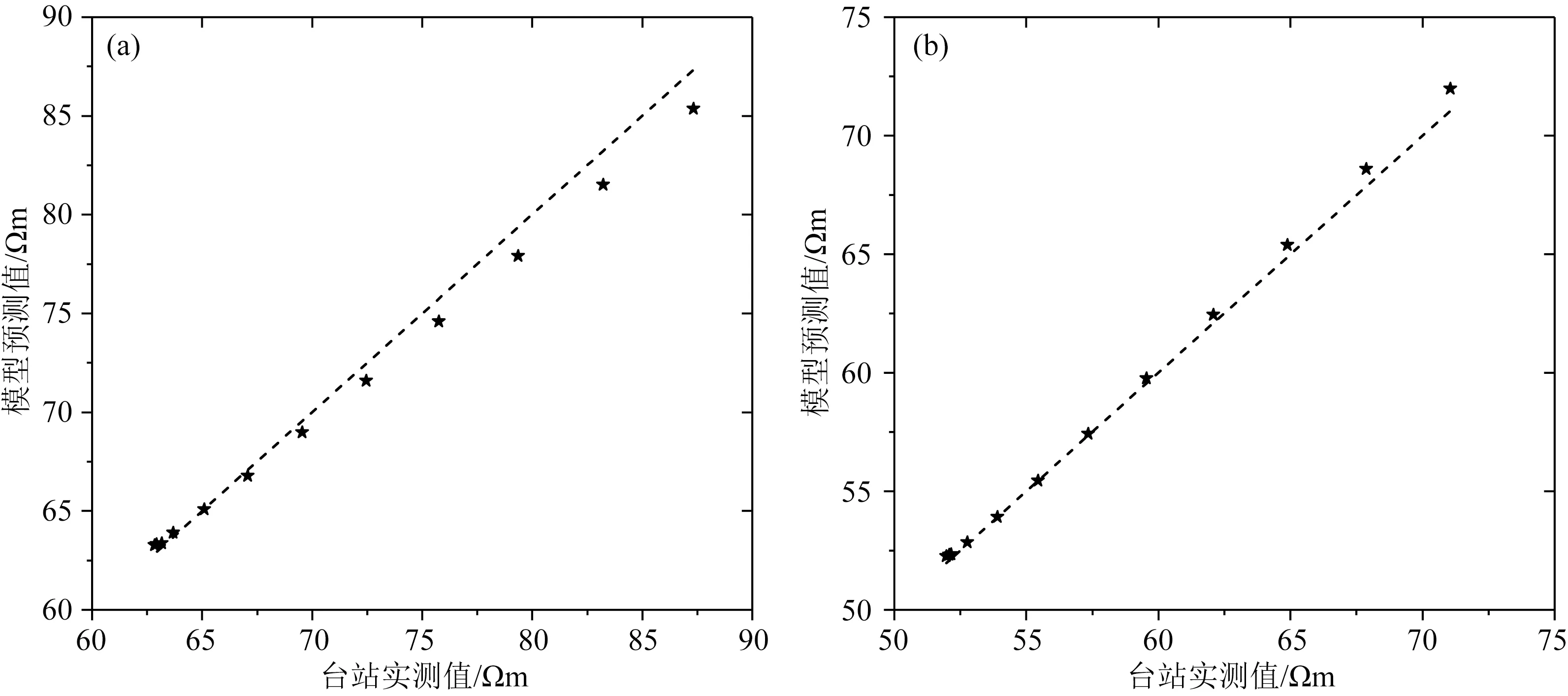
图8 四零四地震台地电阻率模型预测值与台站实测值对比
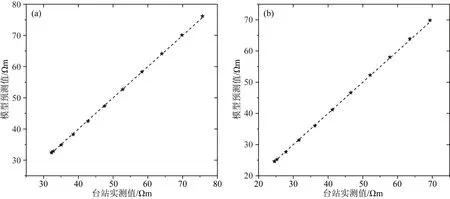
图9 乌加河地震台地电阻率模型预测值与台站实测值对比
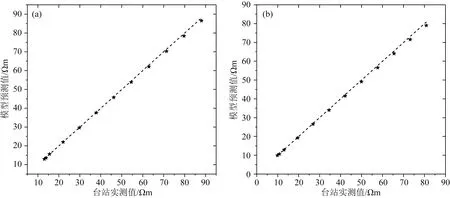
图10 青光地震台地电阻率模型预测值与台站实测值对比
结果显示,对于同一台站的同一测向,在供电线与测量线间距离、平行长度、地电阻率和装置系数等参数均已知的条件下建立的地电阻率交流观测的电感性耦合模型,供电频率范围0.1~10 Hz时,其模型预测值与采用地电阻率交流观测系统在试验台站的实际观测值间的误差不大于2 Ωm,且误差的平均值小于0.9 Ωm,误差的均方根小于0.7 Ωm,最大相对误差不大于2.4%.说明本文建立的地电阻率交流观测的电感性模型的预测结果较试验台站的实际观测结果的偏离程度较小,预测值和实测值吻合,可以认为该模型在不同的供电频率处均能够较好的反映台站的实际观测情况,证明了模型的有效性.
综上所述,本文建立的电感性耦合效应模型能够较好的反映台站实际受到的电感性耦合效应影响,在已知观测装置相关参数的基础上能够较好的预测出地电阻率交流观测结果.因此,可以将此电感性耦合模型应用于台站地电阻率交流观测试验,预测交流观测结果,验证试验结果的正确性;此模型也将进一步用于消除电感性耦合效应影响的数据处理方法的研究中.
4 讨论与结论
地电阻率交流观测方法能够有效抑制地铁、轻轨等城市轨道交通的干扰,然而不同频率的交流观测值与直流观测值存在细小差别,通过分析地电阻率交流观测值随供电信号频率变化的特征可知,随供电信号频率增大,地电阻率交流观测值逐渐增大,且电压测量值的相位超前于电流测量值的相位,相位差为正值.因此,电感性耦合效应为地电阻率交流观测过程中的主要影响因素.
本文通过建立地电阻率交流观测系统的电感性耦合模型,正演模拟分析了供电信号频率、地电阻率值、以及供电线与测量线间距离、平行长度等参数对地电阻率观测误差的影响,得到地电阻率交流观测中电感性耦合效应的特征:电感性耦合随供电信号频率的增大而增大,随供电线与测量线间距离增大而减小,随地电阻率值的增大先上升后下降,曲线中会出现峰值;同时,随着供电信号频率减小,或随着线间距离增大,电感性耦合影响造成的地电阻率观测误差范围也相应地减小,当误差范围减小到一定程度时,单独降低供电信号频率,或单独增大线间距离,都不能够明显改善电感性耦合效应对交流观测结果的影响.
当地电阻率大于10 Ωm,线间距离大于0.01 m时,采用低于0.1 Hz频率的供电信号,观测误差小于0.14 Ωm;当地电阻率大于100 Ωm,线间距离大于1 m时,采用低于1 Hz频率的供电信号,观测误差小于1.01 Ωm,此两种情况可以满足地电阻率观测所需的精度要求.目前我国使用的地电阻率观测台站,绝大多数地电阻率观测值在10 Ωm以上,因此,选择低于0.1 Hz的供电信号能够有效消除电感性耦合效应的影响,获得较高质量的观测数据.此外,对于在低频段受到干扰的部分台站,可以选择更高频段进行观测,如果地电阻率在100 Ωm以上,可选择0.1~1 Hz频段的供电信号,同时将供电线与测量线间距离增大至1 m以上,能够有效消除电感性耦合效应的影响.
通过将本文建立的地电阻率交流观测的电感性耦合效应模型应用于台站实际观测试验中,对比利用模型计算的地电阻率预测值和试验台站的实际观测值,二者在相同的参数条件下的计算误差均小于2 Ωm,误差的平均值小于0.9 Ωm,误差的均方根小于0.7 Ωm,最大相对误差不超过2.4%,证明该模型在观测系统的供电频率范围内均能够较好的模拟台站的实际观测,获得吻合性较好的模型预测结果.因此,可以将本文建立的电感性耦合模型应用于台站的地电阻率交流观测试验,预测交流观测结果,验证试验结果的正确性;对于不能够满足地电阻率值和供电频率要求的台站,可以根据本文建立的电感性耦合模型对观测值进行数据处理,从而消除电感性耦合效应的影响.
致谢本研究在试验过程中得到了中国地震局地震预测研究所赵家骝研究员的指导,得到了嘉峪关地震台、四零四地震台、乌加河地震台、青光地震台等多个台站工作人员的大力支持和协助,两位审稿专家对本文提出了建设性的修改意见和建议,作者在此一并表示感谢.
