“角的初步认识”教学与反思
2023-01-10江苏涟水县淮文外国语学校223400朱幼林
江苏涟水县淮文外国语学校(223400) 朱幼林
【教学内容】苏教版教材二年级下册第84~85页的例1、例2。
【教学目标】从数学的角度了解角的结构和名称,初步学会画角,自制度量工具比较角的大小,体验策略的丰富性;形成观察力和空间想象力,学会辨认实物和图形中的角,在合作探究中形成团队协作精神和沟通能力。
【教学过程】
一、激趣导入,出示课题
师(出示图1):哪个图形比较特殊?说一说它特殊在哪里。

图1
生1:长方体,它特殊在是三维结构。
生2:圆形,它全部由曲线围成,没有角,其余图形都有角。
(设计意图:课前展示各种图形,是对以往所学知识进行总结梳理,为学习新知提供丰富表象,从常见几何图形中寻找“角”的身影。)
二、引导探究,建立表象
师:今天,我们学习一种简单特殊的平面图形——角。
1.调研认知起点
师:你心目中的角是什么形态?能具体指认一下吗?
(设计意图:通过回顾基本几何图形形态的特征,摸清学生的功底,抓住学生对角的初步印象,借此开展教学,可以在第一时间让学生建立数学意义上的角,与生活中的角划清界限。)
2.逐步深化丰富认知
师:看来,大家对角还是有一些误解。数学中的角可能与你心目中的角有些不同。想一睹数学中角的真面目吗?请看大屏幕,不要眨眼噢!
师(电脑演示):看出什么端倪了吗?看完屏幕上的角后,再来指认三角板上的三个角。
(设计意图:借助学生的认知起点,一开始就进行专业辨识训练,学生意识到数学中所言的角很具体,除了通常意义上的两边和顶点,两边包夹的部分也属于角这个图形的结构。)
3.感知抽象
师:不仅是作图工具三角板上有角,生活物品上也能抽象出数学意义上的角。(出示图2)这些物品上都有角,你能准确定位并指出吗?
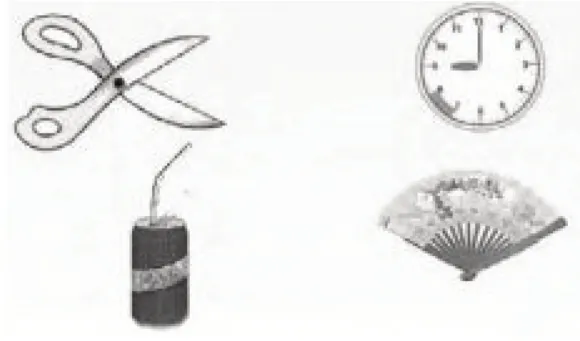
图2
师:观察图3,这是由图2简化而得的,有什么相似之处?(都有一个顶点、两条边)

图3
师(出示图4):判定下列图形属不属于角,并说出理由。
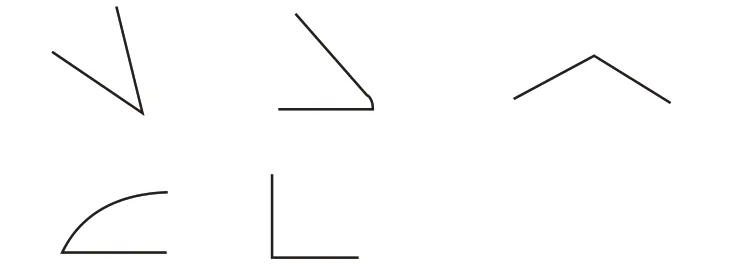
图4
角是一个简单的几何概念,说它简单,是因为其结构形式,但比起线段、射线、直线,它既具有一维空间的影子,又具有二维平面图形的形貌。直观教学是低年级教学的常用手段,形象思维是低龄儿童的主要思维方式。生活中的角与几何中的角有很大的差别,这个生活表征比“线”形象,但是比其他几何体模糊,这才是教学的难点。比如直线,生活中很难找到向两端无限延长的实物与之对应;对于三角形,生活中又很容易找到与之高度吻合的实物;而角的实物表征则处于一种虚实难辨的模糊状态。几何中的角是有固定大小的,如果将两块木片用一颗螺钉连起来,则可以随意开合,因此,角的教学既要以生活材料为表征,又要从生活表征中抽象出标准的几何角的形态,这个需要高超的课堂教学手段才能做到。
三、动手操作,丰富表象
1.找角
师:寻找身边存在的角,并说说它的顶点和边各在哪里。在平面图形和长方体上寻找,尤其是长方体。
(设计意图:从立体图形中找角,既能冲破实物的束缚,又能将角的概念严格限制在平面图形的范围内。)
2.做角
师:用材料(吸管、细线、圆形纸片、三根小棒)制作角,四人合作探究。
生1:用绳子拉出一个角。
师:为什么绳子要绷紧?绳子为什么要多出一个拐点?指出角的顶点和边,平常所言的角具体指哪个区域?
生2:用硬纸折角。
师:折法不同,折出的角就不同。
生3:用小棒摆角。
师:摆法不同,形成的角的数量就不同。
生4:用吸管做角。
师:怎样将角扩大?如何将其缩小?
师:两边开口越大,代表着角越大,两边开口越小,代表角越小。
师:制作好一个角后,随意改变其大小,最大是多大,最小又是多小?要改变角的大小,关键在于改变什么?
师:同桌合作,一人先做一个角,另一人做一个更大的,再做一个更小的,然后交换任务。
师:比角的大小时,主要是看什么指标?
生5:比两边开口的大小。
师:与同桌制作2个大小相等的角。
(设计意图:由于活动角的边长可以伸缩,学生可能朦朦胧胧觉察到边的长短与角的大小关联非常微弱,此环节就是为了再次加深学生的认识——二者毫不相干。尽管这节课不需要明言,但要想让学生对角建立正确、清晰的表象,就必须使学生对角的大小有一个准确的认识,因为角的抽象性主要体现在大小上,这其实是一个难点。因此,笔者设计这一活动的初衷,是让学生在做角的过程中一直关注和控制角的大小,这样自然会发现边的长短不影响大小设定。历经三次操作,虽未明言,但是学生早已心领神会,这就是用事实说话,事实胜于雄辩。)
角是一个特殊几何图形,特殊之处就在于其边长可以无限延长,其大小与两边长度无关,只与开口大小有关,但是,角又必须包含两边在内。学生理解的生活中的角其实就是那个“尖端”,但是这个“尖端”只是两条射线重合的端点而已,在生活实物中可以淡化两边的存在,但是放到几何中,两边是构成角的基本元素。这样,生活角与几何角的差异化就会干扰学生对几何中的角的正确理解。如果让学生抛开直观思维从抽象维度去理解几何角,无异于空中楼阁、水中捞月,当在生活中很难直接找到现成的表象材料时,亲自动手做角,则不失为一个万全之策,学生既可以从中提取必要的实物表征(做出心目中那个“尖角”),同时又能达到几何特征的渗透。
3.画角
师:独立画角,并说说你是如何画的?
师:谁的办法更好?说出你的理由。
师(画锐角、直角):我画出的两个角,哪个大一些?这个角(指直角)是不是似曾相识?
师:想一想,要画出一个与这两个角都不一样的角,怎么画?
做角可以让学生通过实践活动亲身体验到角的几何特性,但是学生依然摆脱不了实物表象的束缚和干扰。数学来源于生活又要脱离生活,几何来源于实物又要独立于实物之外。在做角的操作中,学生仍然需要借助实物塑造出与几何中的角相近的表象,其实就相当于在实物角和几何角之间制造一个“杂交模型”,而画角的操作可以彻底摆脱实物的羁绊,完全向着抽象思维演化——画角时,学生会将实物边(木条、吸管、毛线)抽象成几何射线,然后将实物边抽象成两条射线的端点重合,自然形成“夹角”。在画角的过程中,可以随意伸缩边长,也能让学生感知到角的大小与边线长短无关。
【教学反思】
通过多次摸索,笔者归纳出提高教学效率的三大因素:一是学习起点;二是教学目标;三是教学策略。
一、摸清学生的真实起点
在新授课之前,教师总会与学生交谈,这些交谈的素材都能为改进教学提供可靠数据。笔者对学生的学习起点做了细致分析。
1.从教材的编排看。“角的初步认识”是继承初步认识长方形、正方形、三角形的教学,开启后续深入学习角的序幕。对二年级的学生而言,角的图形很抽象,因此教材先呈现情境图,展示各种生活中的角,并抽象出几何形态上的锐角、钝角和直角;直接用图形揭示角的概念,并标出顶点和边,凸显角的结构特征;通过制角、折角等活动,再次展现角的形态特征,使学生直观地认识到角是有大小的。
2.从知识经验看。角与生活息息相关,二年级的学生已经7岁,具有一定的生活经验,也具备直观思维能力,能够找到生活中的角。因此教师要引导学生摆脱实物的桎梏,经历抽象的过程,感受数学的实用性,让他们学会用几何的视角审视角。另外,教师还可以通过让学生操作角,获得对数学角的直接经验。
二、教学目标恰当
一节课的成败与教学目标制定得是否恰当有关。教学目标的确定,需要综合考虑课程标准、教材和学情三大要件,做到“隐性目标”与“显性目标”兼顾、“近期目标”和“远期目标”结合,这样的教学目标才科学合理。
三、选定教学策略
教学策略就是为了达成教学目标。任何教学策略都有明确的指向性和适用范围,规范着教学行为。在本节课中,感知角的大小与边长无关是难点,为了顺利突破这个难点,学生花大力气开展操作活动:指角、做角、比角、画角、想角等,自始至终学生都在思考、想象、质疑。比如画角环节,除了操作技能的学习,还有对角的形态构想,根据教师画出的一个锐角和一个直角(没有指明),引导学生想象出钝角,打破了学生只会画钝角的思维定式,也打破了学生对角的认识只局限于直角和锐角的狭隘观点,发展学生的空间观念。在做活动角的环节中,做相等的角也好,比大小也好,就是为了全力揭示角的大小与边长无关的真相,尽管这个结论不必明说,但是这是建立角的正确表象的前提。
