基于QSTFT的同步压缩变换及在轴承故障诊断中的应用

叶杰凯，汤小明，林青云，梁登，吴华盛

(丽水市特种设备检测院，浙江 丽水 323000)

0 引言

信号处理是一种利用数学算子从信号中提取特征信息的反向处理方法。传统的傅里叶方法只能处理平稳信号，并且是基于全局的频谱分析，对于频率随时间变化的非平稳信号往往无能为力。而时频分析方法能够有效地揭示时变性特征，已被广泛应用于从非平稳信号中提取特征信息[1-2]。

传统的时频分析方法有连续小波变换(CWT)和短时傅里叶变换(STFT)，常被用来描述信号在时频平面上的特性[3]。然而，它们都有同样的局限性，就是所谓的“不确定性原理”，即不能在时间和频率上任意精确地定位一个信号，也就是常说的时频模糊问题。这种局限性导致后续的瞬时频率提取和信号重构等方面会存在不足，难以较为清晰地提取出故障信号及其分量。因此，针对时频平面去模糊化的研究一直都是一个热门方向，时频重排和同步压缩变换(synchrosqueezing transform, SST)就是其中一个较好的思路。

自从DAUBECGES I等[4]提出了同步压缩变换来揭示非平稳信号复杂的时频特性，在医学、地球物理学和音频等多个领域对其都有所应用。SST是一种特殊的重分配算法，它对应于一种提高时频分辨率的非线性算子。在SST中，时频系数仅在频率轴上重新分配，使其既能够简化分配过程又能与原始参量保持联系[5-6]。然而，SST只能使瞬时频率“慢变”信号的时频表示锐化，并且当处理强时变信号如非线性调频信号时，SST不能产生集中的时频表达。这是因为SST中的频率重分配算子不能为强时变情况提供准确的无偏估计。为此，PHAM D H等[7]提出了高阶同步压缩变换方法(high-order synchrosgueezing transform, HSST)。在高阶振幅和相位近似的基础上定义了新的同步压缩算子，并对快速变化的瞬时频率(IF)信号产生高度集中的时频表达。但是，HSST是以传统短时傅里叶变换STFT为基础，在时频变换窗宽上无法做到自适应选择。同时，BERRIAN A等[8]提出了基于缝式短时傅里叶变换(quilted STFT, QSTFT)的同步压缩变换方法，即SST-QSTFT。该方法对复杂多组分信号的瞬时频率无法做到准确估计，再加上对噪声极为敏感，因此在强背景噪声下，很难获得清晰的时频表示[9-10]。但是，QSTFT重新定义了一组随时频变化的自适应窗口函数集合，具有明显的自适应特性，其可以使用最合适的窗函数来适应不同的时变信号，自动匹配信号的局部变化，以此来提高STFT的时频分辨率。

综上，本文引入基于缝式短时傅里叶变换QSTFT的自适应窗口计算方法，并将该方法应用到HSST中，提出一种基于缝式短时傅里叶变换的自适应高阶同步压缩变换(adaptive high-order synchrosqueezing transform based on a quilted short-time fourier transform, AHSST-QSTFT)。

1 理论描述

1.1 基于QSTFT的同步压缩变换

定义一个调幅调频(AM-FM)信号，令其表达式为

s(t)=A(t)eiφ(t)

(1)

式中A(t)和φ(t)分别是其瞬时幅值和瞬时相位。

继而信号的STFT变换可以写成下面的形式：

(2)

式中：g(t)是窗函数；g*(t)是g(t)的复共轭。

那么，SST-STFT可以用下面的公式表示：

(3)

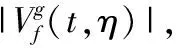
(4)

将时频面任意一个局部区域定义为Ω⊆R2,且该区域对应一个缝窗口函数集合hΩ。令ht,ω=hΩ，对其中每一个(t,ω)∈Ω。则函数集合h的表达式为

h(τ,t,ω)=ht,ω(τ)

(5)

式中t,τ∈R且ω∈R+。

对信号s(t)，本文研究的QSTFT的表达式为

(6)

因此，由式(3)和式(6)可得SST-QSTFT表达式为

(7)

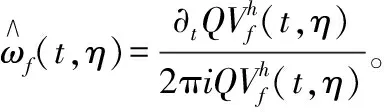
1.2 高阶同步压缩变换

SST采用零阶估计来对信号的频率进行估计，仅在处理慢时变的中频信号时效果较好。而高阶SST方法则是基于信号振幅和相位的高阶Taylor展开，对信号的IF进行更加精确的估计，以此来提高在特征频率上面的能量，达到去模糊化的目的。

AM-FM信号的Taylor展开式如下：

(8)

式中φ(k)(t)表示φ(t)的第k阶导数。

那么，式(2)可以改写成如下形式：

(9)

(10)

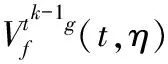
(11)

此时，HSST的表达式可以写成

(12)

1.3 基于QSTFT的自适应高阶同步压缩变换

(13)

最后，根据式(7)、式(11)和式(13)可知，AHSST-QSTFT的表达式为

(14)

因此，本文提出的基于QSTFT的自适应高阶同步压缩变换算法AHSST-QSTFT的具体实现步骤如下：

1)定义缝窗口函数，对STFT的窗函数进行改进，得到自适应窗函数集合；

3)按照式(14)的方法重置高阶瞬时频率估计，从而获得改进的自适应高阶时频表达QHTs(t,ω)，并画出时频图。

2 仿真分析

为了验证该方法的可行性，构造两个具有AM-FM性质的分量信号：

(15)

其中：信号的采样频率设为4 096 Hz；信号长度为4 096；信号的理想瞬时频率曲线如图1所示(本刊为黑白印刷，如有疑问请咨询作者)。为了更加贴近实际情况，使模拟信号更有代表性，将两个信号进行了叠加，并且添加了SNR=-2的高斯白噪声(信噪比公式SNR=10lg(Ps/Pn)，得到信号x(t)的时域波形如图2所示，频域波形如图3所示。由FFT计算的结果可以看出，在噪声干扰较大的情况下，无法从频谱图中区分和辨识时变的信号特征。

图1 信号x1(t)和x2(t)的频率曲线

图2 信号x1(t)、x2(t)和x(t)的时域波形图

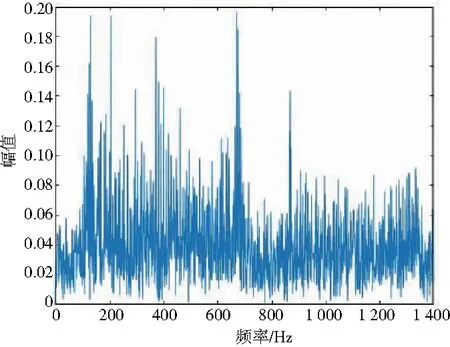
图3 信号x(t)的频域波形图

因此，为了说明本文所提出算法的优势，分别画出了仿真信号的4阶HSST和AHSST-QSTFT的时频图，并且采用相同的脊曲线提取算法对分量进行了提取，结果见图4。其中虚线为真实的瞬时频率，实线为提取的脊线。

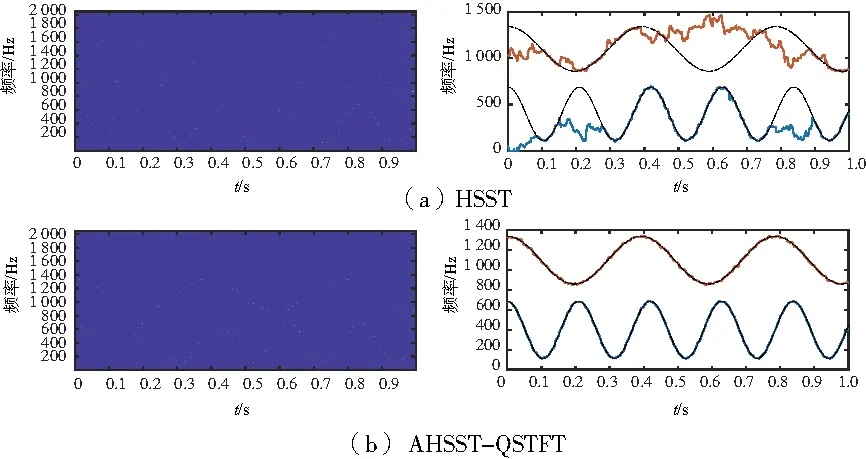
图4 时频表示及其脊线提取结果

通过两组时频图的对比，可以得出AHSST-QSTFT方法能够获得更好的时频表达效果，并且提取到的瞬时频率更加接近于真实情况。

3 实验分析

故障诊断对于机械设备的预知维修具有重要意义。根据RANDALL R B等提出的滚动轴承模型[11]，为了进一步验证基于AHSST-QSTFT方法在机械设备故障诊断中的有效性，本文设计了如下实验。

图5为试验装置的故障模拟器。设备由550 W的交流电机驱动。故障轴承安装在最右侧的皮带轮上，利用电火花加工在目标轴承加工4个点蚀坑，坑的深度为0.8 mm，并尽可能靠近支撑轴承的机壳上方垂直固定振动加速度传感器，用以进行数据采集，传感器位置如图中箭头所示。实验采用B&K3560C数据采集分析仪进行数据采集，采样频率为16 384 Hz，转速1 450 r/min；滚动体个数Z=9，试验中的滚动轴承型号为6207，压力角为α=0°，故障类型为轴承外圈故障，可以根据下面的计算得到故障频率：

图5 轴承故障模拟实验台

(16)

式中：fr为转频，Hz；fo为轴承外圈故障特征频率，Hz。

选择8 192个采样数据分析，实际测得的轴承振动信号如图6所示，在时域波形上能够明显看出瞬态冲击故障。图7是该信号的频谱分析，可以观察到峰值区域主要集中在1 000 Hz、4 000 Hz附近。这是因为轴承发生故障时，当转子经过缺陷位置时，相当于是在轴承上加上了一个冲击力所激发出来的信号，反映的是该系统的固有频率。

图6 实测信号的时域波形

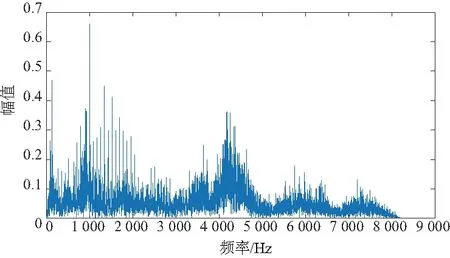
图7 实测信号的频谱图

考虑到实际信号的能量都集中在共振区间，不利于最终故障的识别。因此在本文中首先对实际信号进行希尔伯特变换，得到对应的包络信号，然后再采用AHSST-QSTFT方法对信号进行时频分析。

图8(a)和图8(b)分别是在相同的参数设置下采用HSST和AHSST-QSTFT方法得到的时频表示。考虑到轴承外圈的故障频率为87.01 Hz，一般地，如果能够找到故障特征频率对应的多个倍频就能够确定故障。图8(a)虽然能够较为模糊地看到某些对应的特征频率，但受到背景噪声的影响，它们在时频平面上表示得并不是很突出。图8(b)为采用提出的AHSST-QSTFT方法得到的时频表示，相比于图8(a)，在图中可以清晰地看到故障特征频率fo(87.01 Hz附近)及其2倍频(174 Hz附近)、3倍频(262 Hz附近)、4倍频(349 Hz附近)、5倍频(436 Hz附近)、6倍频(523 Hz附近)、7倍频(610 Hz附近)瞬时频率曲线，并且它们基本上凸显在时频平面上，因此，可以准确地判断故障类型为轴承外圈故障。

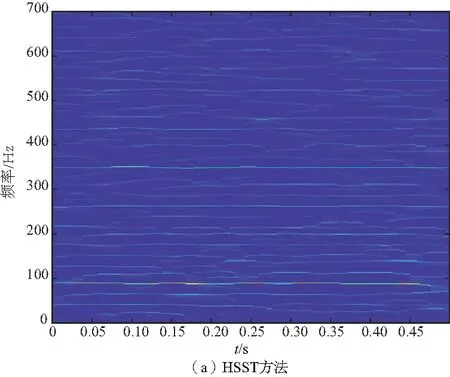
图8 不同方法得到的时频表示

实验结果表明，AHSST-QSTFT方法相较HSST具有更好的抗噪声干扰能力，其最大程度地凸显了故障特征信息，增强了时频平面故障特征的辨识度。

4 结语

本文提出了一种基于QSTFT的自适应高阶同步压缩变换算法，充分利用了QSTFT的窗口自适应性和HSST的时频压缩特性。该方法提高了经典STFT框架下振动信号的窗口选择适应性，使重排后频率估计最大程度地接近信号的真实瞬时频率，提高了时频平面的清晰度，进一步增强了HSST方法在处理时变信号时的分辨能力。同时，数值仿真和轴承外圈故障实验表明，本文提出的方法能够有效降低噪声的干扰，并且在提取更为准确的故障特征信息方面更具优势。