基于MSTMM的超精密飞切机床动态特性分析

2023-01-10何梓锋丁建国常宇

机械制造与自动化 2022年6期

何梓锋，丁建国，常宇

(南京理工大学理学院，江苏南京 210094)

0 引言

2021年我国“十四五”规划提出，要深入实施制造强国战略，加快推进制造业高质量发展。超精密加工技术是航空航天和国防科技等领域发展的基石，更是国家核心竞争力之所在。超精密机床是实现超精密加工的关键装备，其动态特性研究是机床结构、隔振系统设计及优化的基础。因此，寻求一种准确高效的动力学方法，求解其动态特性，全面提升加工精度及加工质量，具有重要的理论意义与工程应用价值。

目前，一些学者开展了超精密飞切机床动态特性方面的研究。邵传东等[1]基于分子动力学原理建立了机床空气静压主轴的分子动力学微观模型，研究了不同设计参数条件下空气静压主轴气膜刚度的变化规律。戴新泽等[2]利用能量法建立机床进给系统动力学模型，计算了其前6阶固有频率。CHANG Y等[3]提出一种改进的计算螺栓结合部接触刚度理论，将多体系统传递矩阵法(transfer matrix method for multibody systems, MSTMM)与分形接触模型结合，建立了考虑螺栓结合部接触特性的动力学模型，更精确地预测了机床的动态特性。LU H J等[4]将主轴考虑为柔性体，应用MSTMM对机床建模与仿真。商兴莲等[5]运用MSTMM求解机床的固有频率，结合模态试验数据采用多岛遗传算法实现了机床前6阶固有频率的识别。

对超精密飞切机床动态特性的研究主要可分为针对局部关键部件和针对整机系统的仿真分析。由于整机的建模较为复杂，采用有限元建模方法进行仿真分析存在计算效率低等问题。为此，有必要发展一种准确高效的动力学计算方法进行动力学分析。MSTMM具有计算量小、程式化程度高的特点，可作为快速计算超精密飞切机床动态特性的一种重要方法。本文采用MSTMM建立考虑立柱、横梁、主轴和刀盘变形的超精密飞切机床动力学模型，并推导总传递方程，使用自适应遗传算法识别系统前18阶固有频率，以期准确高效地求解系统动态特性。

1 超精密飞切机床动力学建模

针对复杂多体系统特征值问题快速计算实际工程急需、有限元法难以承受大系统巨大计算工作量和大刚度梯度引起的计算病态等问题，芮筱亭等[6]首次提出多体系统传递矩阵法并将其广泛用于大型机械系统的动力学分析与设计中，解决了复杂多体系统固有振动特性的计算病态,提高了计算效率。

1.1 模型建立

超精密飞切机床的实物如图1所示，包含床身、工作台、左立柱、右立柱、横梁、左导轨、右导轨、电机定子、电机转子、主轴、刀盘与刀架等主要部件。

图1 超精密飞切机床

该动力学模型含27个体(13个无质量梁、5个刚体和9个集中质量)与11个铰，如图2所示。其中x轴为工件装夹平面内进给运动垂直方向，y轴为进给方向，z轴为切深方向。模型中采用集中质量法描述关键部件的柔性变形，把无限自由度的连续构件处理为若干个有限自由度的离散集中质量与无质量梁。主轴视为1段无质量梁与1个集中质量；左、右立柱、横梁分别视为2段无质量梁与1个集中质量；刀盘视为6段无质量梁与5个集中质量，如图3所示。将导轨与直线电机合并入床身中视为1个整体，电机定子计入横梁中。

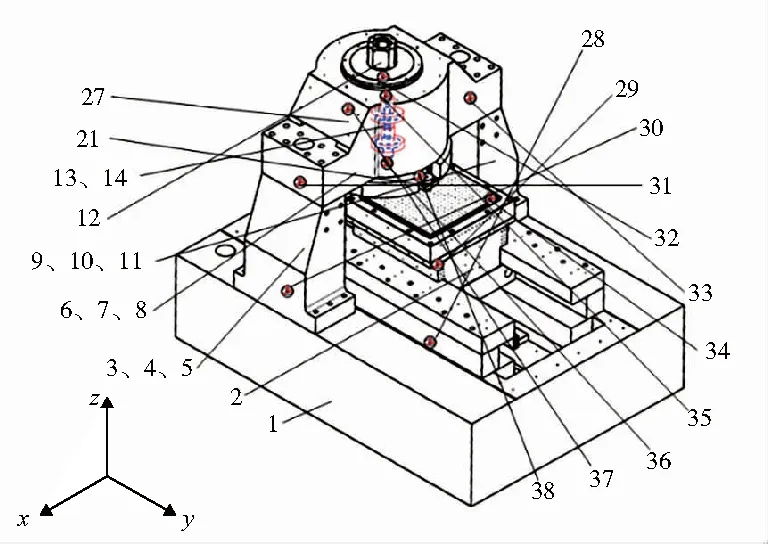
图2 超精密飞切机床动力学模型

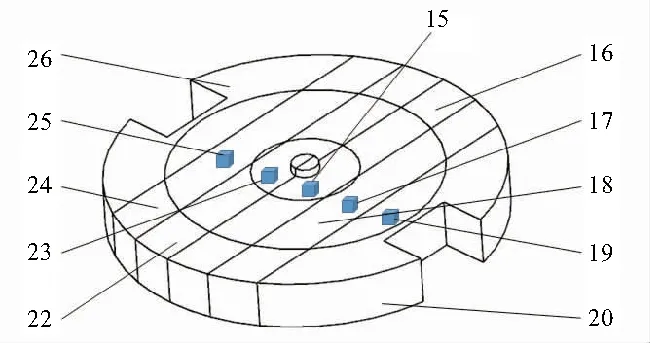
图3 刀盘模型

动力学模型中的元件序号及对应名称见表1。

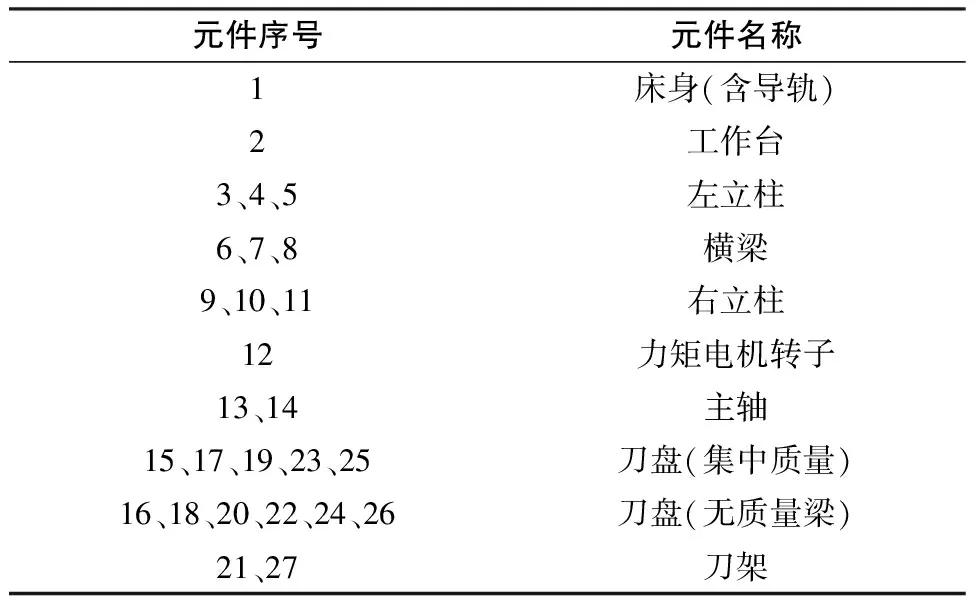
表1 元件序号及对应名称

根据机床系统动力学模型得到系统拓扑图，如图4所示(其中圆角矩形表示弹性梁，矩形表示刚体，圆圈表示集中质量，箭头表示弹性铰)。本模型为含有1个闭环的闭环多体系统，在铰34处切断，原系统变为含有6个树梢的树形多体系统，其树形拓扑图如图5所示。

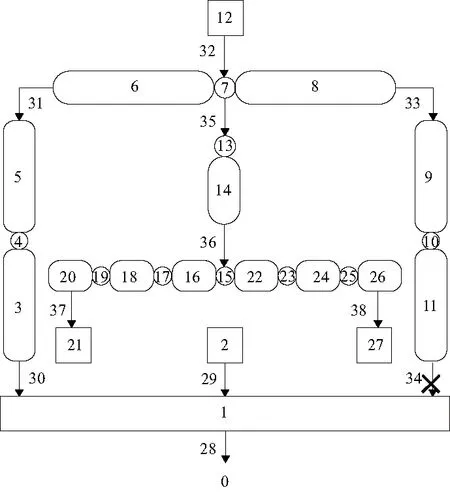
图4 超精密飞切机床动力学模型拓扑图

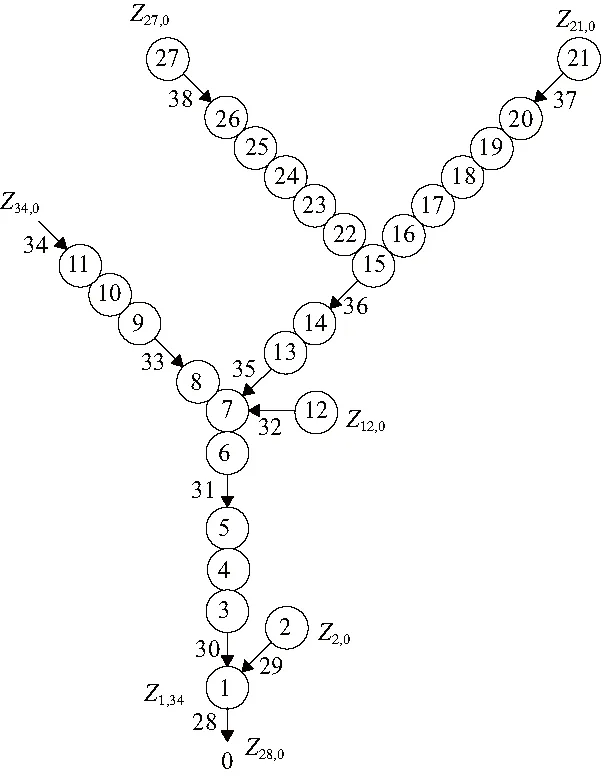
图5 超精密飞切机床动力学模型树形拓扑图

1.2 系统总传递方程

根据MSTMM，定义系统传递点与边界的状态矢量：

Zi,j=[X,Y,Z,Θx,Θy,Θz,Mx,My,Mz,Qx,Qy,Qz]T

(1)

式中：Zi,j表示模态坐标下第i号元件与第j号元件连接处状态矢量，边界处j=0;向量元素依次表示模态坐标下的空间线位移、角位移、内力矩和内力列阵。

由树形多体系统的总传递方程自动推导定理[7]，各个体均处理为单端输入单端输出或多端输入单端输出元件，边界处(利用几何关系合并闭环处)状态矢量为

(2)

地面处为固定端，工作台、电机定子和左右刀架处为自由端，34号铰为闭环切断处新产生的边界，边界条件为

(3)

式中j=2,12,21,27。

(4)

(5)

主传递方程为

-Z28,0+T2-28Z2,0+T12-28Z12,0+T21-28Z21,0+

T27-28Z27,0+(T34-28+T1-28,I1C)Z34,0=0

(6)

将式(6)改写成矩阵形式，即可得到总传递方程

Uall·Zall=0

(7)

式中总传递矩阵为

(8)

其中

(9)

沿传递路径依次连乘各传递矩阵，可得主传递方程中系数矩阵T；沿传递路径依次连乘各传递矩阵并左乘几何矩阵，可得几何方程中系数矩阵G。

各元件传递矩阵由参考文献[7]中的传递矩阵库改写而成。无质量梁均考虑剪切变形，立柱考虑轴向压力。式(7)中除全部11个铰的刚度未知外，全部参数均可由UG图样中物理参数计算得出，立柱、主轴与刀盘中无质量梁的长度由有限元软件Abaqus计算静力位移后等效得出。

由于Zall第1～6、19～24、31～36、43～48与55～60行为0，去掉Uall对应列，即可得42阶方阵U42×42。式(7)可简化为齐次非线性方程

U42×42·Z42×42=0

(10)

由线性代数易知，在U42×42的行列式等于0时，式(10)有无穷多个非零解ω。

|U42×42|=0

(11)

因弦截法具有无需求解导数、迭代次数较少的优点，本文采用弦截法结合逐步扫描法对式(11)进行求解，计算系统前18阶固有频率。

2 基于自适应遗传算法的参数识别

遗传算法是HOLLAND教授受生物学中自然遗传的基本原理启发提出的一项适于复杂系统优化的技术，之后用于函数优化与组合优化问题中[8]。为防止未成熟收敛，SRINVIVAS M等[9]提出一种自适应遗传算法，交叉概率Pc和变异概率Pm能随适应度自动改变。

本问题可描述为多目标优化问题，其数学模型为

(12)

式中：根据结构的对称性有19对相等的刚度，余下47个刚度即为待识别的参数；k为47×1刚度向量；fn(k)为第n阶频率计算值。

根据参考文献[10]中模态试验的数据。使用权重系数法设计适应度函数，完成多目标优化向单目标优化的转换。

(13)

式中：fn(k)为第n阶频率计算值；ωn为第n阶频率试验值。

使用自适应遗传算法识别各刚度参数，结合实际问题，过程中的控制参数设计如下。

个体数量设为40，每个个体包含47个决策变量；最大遗传代数设为1 000；采用实值编码，变量范围设为[105,1013]；采用随机遍历抽样的排挤选择算法，代沟设为0.8；采用离散重组，交叉率设为1；采用自适应变异算子，设置自适应变异概率Pm，其表达式为

(14)

式中：umax表示群体中最大的适应度值；uavg表示每代群体的平均适应度值；u表示要变异的个体适应度值；Pm1根据本次实际问题设为0.02。

结合多种群遗传算法，子种群数设为8，迁移概率设为0.2，每20代基于适应度向近邻结构移民。

超精密飞切机床参数识别过程如图6所示。

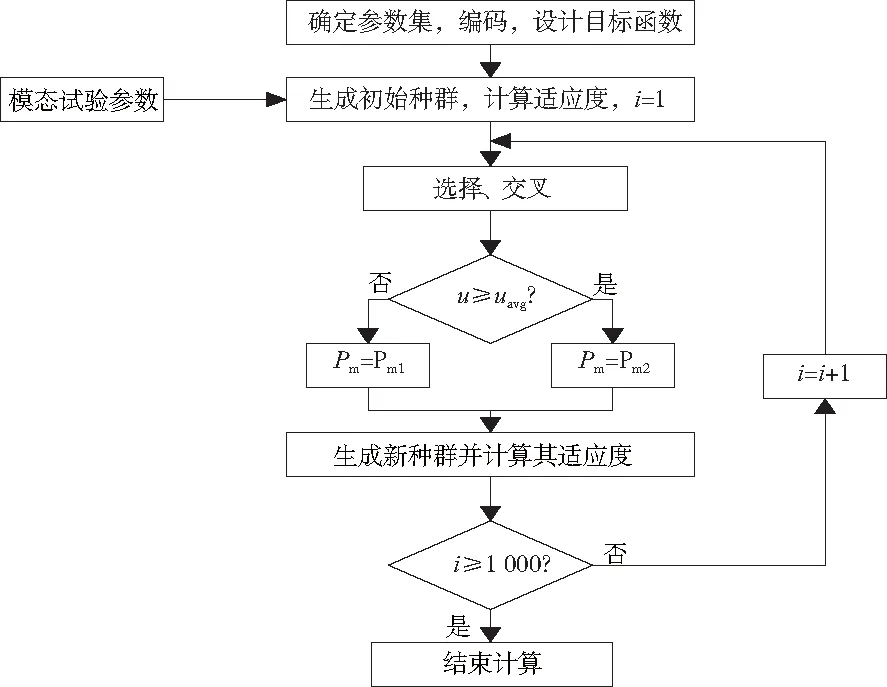
图6 自适应遗传算法参数识别过程

运行上述自适应遗传算法识别参数，每代目标函数均值变化和最优解变化如图7所示。运行变异概率0.02的简单遗传算法对照如图8所示。

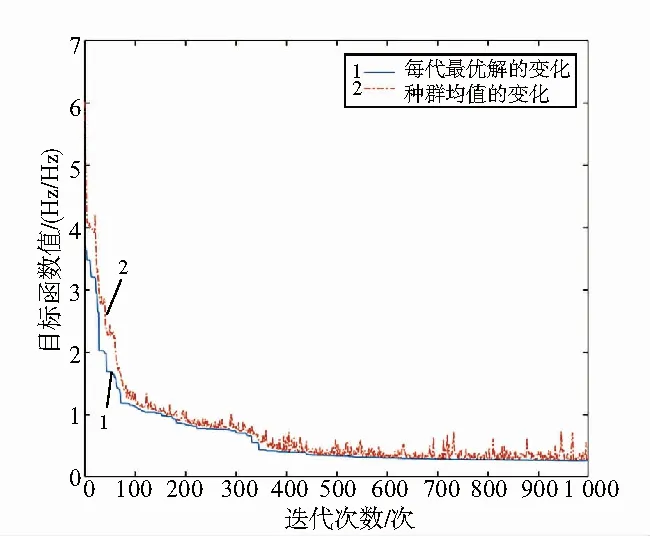
图7 自适应遗传算法每代种群最优解与目标函数均值

图8 简单遗传算法每代种群最优解与目标函数均值

对比图7与图8，采用实值变异的简单遗传算法在第220代左右趋于稳定，陷入局部最优。本文采用的算法在350代左右发生转折，说明搜索到了新的极小值。后续仍有较多新个体产生，最终收敛到了全局最优解。

识别出的刚度加上由于结构对称性无需识别的刚度，共计66个刚度，其具体参数如表2与表3所示。

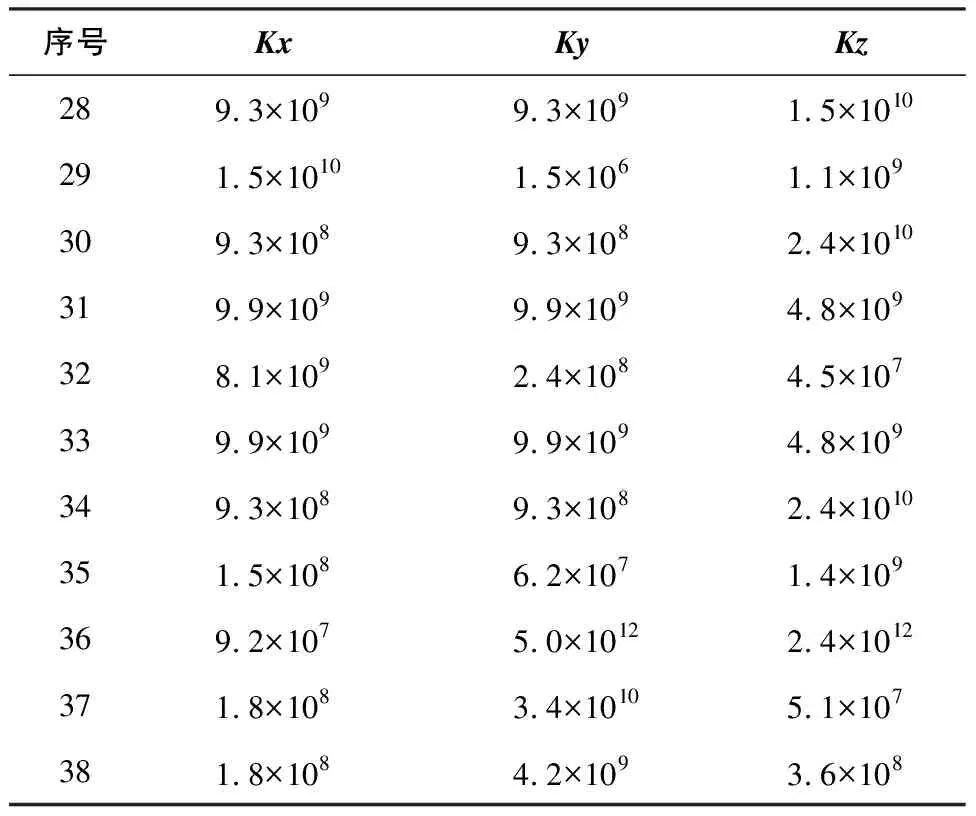
表2 11个铰的线刚度单位：N/m

表3 11个铰的角刚度单位：Nm/rad

3 超精密飞切机床动态特性分析

把铰的刚度代入总传递方程(7)可解出系统固有频率，计算过程如图9所示。

图9 超精密飞切机床固有频率计算过程

为与MSTMM法对比计算精度及效率，本文采用有限元软件Abaqus对超精密飞切机床进行建模与模态分析。部件采用实体四面体单元C3D4网格和实体六面体C3D8R网格，划分后整机共206 887个网格单元，如图10所示。采用Lanczos法进行模态分析。

图10 超精密飞切机床有限元模型

分别使用有限元与MSTMM求解超精密飞切机床固有频率，有限元计算值及相对误差、MSTMM计算值及相对误差如表4所示。

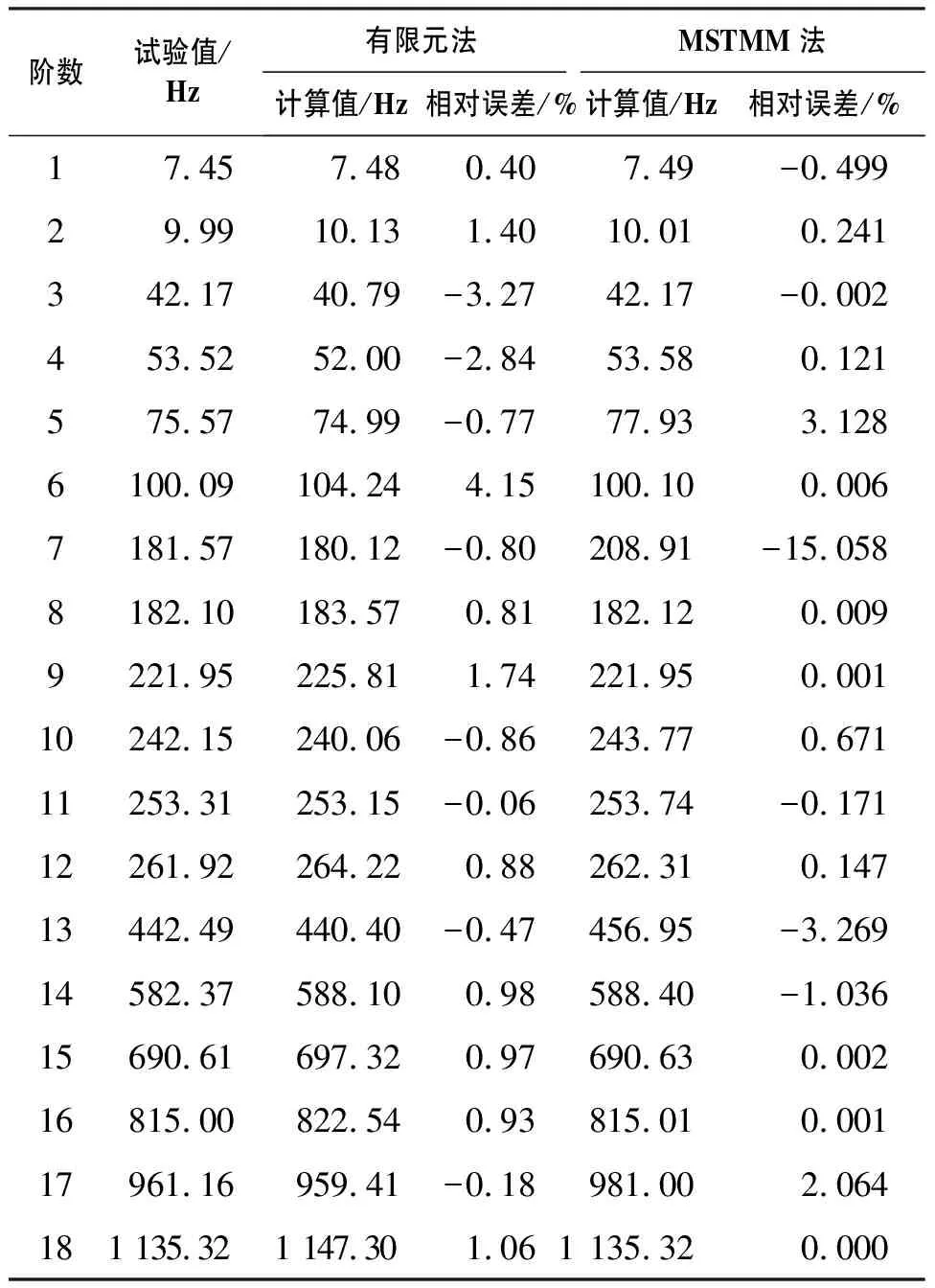
表4 频率试验值、计算值与相对误差

两种方法各运行10次取平均值，有限元平均计算时间为310 s，MSTMM平均计算时间为4.5 s，计算效率提升了近70倍。

计算结果表明，MSTMM计算值除第7阶频率误差略大外，其余各阶频率误差均在5%以内，识别结果与试验值较为一致，证实了计算模型准确可靠。在高阶频率中，反映刀尖局部振型的第12、14阶频率也较为吻合。分析误差原因为第7阶频率与第8阶过于接近，是结构对称引起的重根模态，由于算法的原因只能搜索到异号的单根。