基于深度学习的区域供热逐时负荷预测研究

尚海军 白新奎 乔磊 邓秦生 白旭 李恭斌 孙玉成 尹军波 刘圣冠 耿如意

1 西安西热节能技术有限公司

2 华能甘肃能源开发有限公司

3 华能兰州新区热电有限公司

0 引言

区域供热作为北方地区建筑空间采暖的主要方式，目前仍以煤燃烧作为热量的主要来源[1]，已对实现双碳战略目标构成严峻挑战。为降低区域供热系统的运行时能耗，供热负荷的精确预测已成为实现适量供热的关键[2]。已有大量研究人员采用人工神经网络（Artificial Neural Network,ANN）对供热日负荷进行预测[3-5]，但区域供热系统在实际运行时需以小时为单位对供热量进行调节，且ANN 作为一种浅层的神经网络模型在处理大规模具有不确定性的数据时，预测精度往往偏低[6-7]。针对上述问题，本文提出一种基于深度学习的供热逐时负荷预测方法，可为实现区域供热高效运行控制提供新的思路。

1 深度置信网络结构及原理

深度置信网络（Deep belief Network,DBN）作为一种深度学习方法由人工神经网络发展而来，其本质为将输入变量特征转化为概率形式进行输入，并采用逐层贪婪算法逐层进行训练，有效克服了深层神经网络训练难的问题[6-7]，特别适用于高维具有不确定性数据的分类，现已在电力负荷预测中得到广泛的关注[8-10]。

DBN 由若干个受限玻尔兹曼机（Restricted Boltzmann machines,RBM）和BP 神经网络组成，RBM作为DBN 的关键组成元件，其具体结构如下图1 所示。RBM 由可见层和隐含层组成，各层神经元之间相互连接，层内无连接，隐含层取值通常符合伯努利分布形式，即0 或1，分别代表神经元“未激活”和“激活”。在DBN 中，第一个RBM 隐含层为第二个RBM的可见层，依次类推，即RBM 的个数等于DBN 隐含层个数，而最后一个RBM 隐含层则作为BP 神经网络的输入层。DBN 学习阶段分为“预训”和“微调”两个阶段，其中“预训”阶段为无监督学习即通过堆叠RBM对数据的特征进行准确抽象地提取，而“微调”阶段为有监督学习即通过误差反向传播算法BP 神经网络对整个网络进行调优。

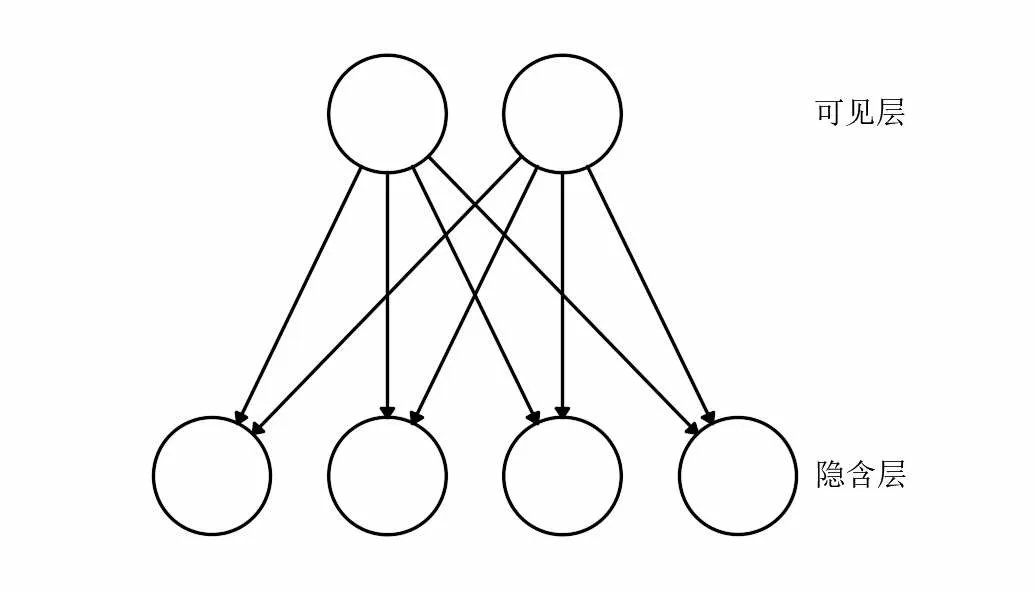
图1 RBM 结构示意图

RBM 采用能量函数描述整个系统的状态[11]，对于伯努利分布的可见层和隐含层，能量函数如下式（1）：

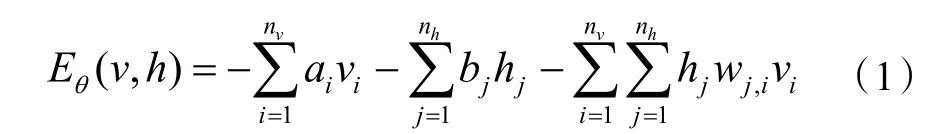
式中：vi为可见层第i 个神经元取值；hj为隐含层第j个神经元取值；ai为可见层第i 个偏置取值；bj为隐含层第j 个偏置取值；wj,i为可见层第i 神经元与隐含层第j 个神经元的权值；nv为可见层神经元个数；nh为隐含层神经元个数。

可见层与隐含层的联合分布概率如下式（2）：

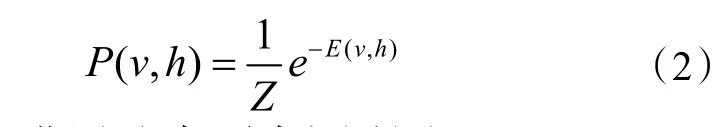
式中：Zθ为归一化因子，如下式（3）所示：

可见层边缘分布计算如下（4）：

隐含层边缘分布计算如下（5）：

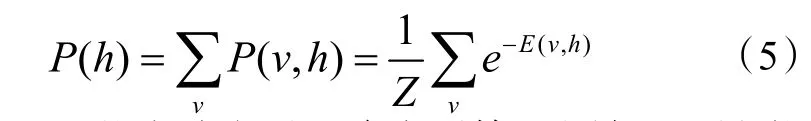
当可见层状态确定时，隐含层第j 个神经元被激活的概率计算如下式（6）：

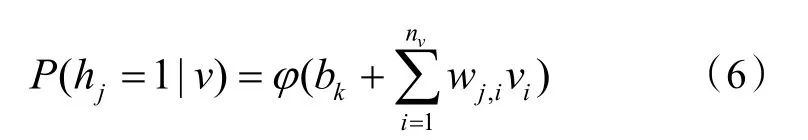
式中：φ 为激活函数，通常取为Log-sigmoid 函数形式。

当隐含层状态确定时，可见层第i 个神经元被激活的概率计算如下式（7）：

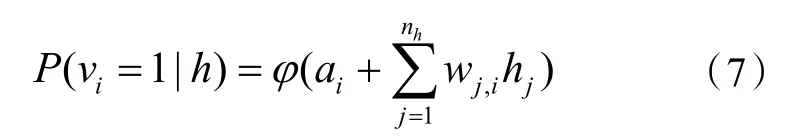
由于篇幅有限，RBM 的训练过程此处不再赘述。

2 数据来源及深度置信网络模型的建立

2.1 数据来源及输入参数的确定

以兰州新区某区域供热换热站为例对所提出方法的有效性进行验证，该换热站承担建筑采暖面积为164257.87 m2，采暖热指标为77 W/m2。由于供水温度，回水温度，循环流量和室外温度已被多个研究证明具有强相关性[3-4]，此外，在空调负荷预测中为考虑到建筑物的热惰性，常取预测时刻前2 小时的数据作为输入参数[12]，本研究分别将预测t 时刻前1 h，1～2 h 和1～3 h 的供水温度，回水温度，循环流量和室外温度及预测t 时刻的室外温度作为输入参数。输出层选取预测t时刻的供热负荷作为输出参数。选取2019 年1 月2 日到1 月15 日换热站逐时运行数据共336 组样本作为数据集，其中前192 组作为“预训”训练集，中间72 组作为“微调”训练集，后72 组作为测试数据集。

2.2 深度置信网络各参数的选取

本文通过堆叠三个RBM 和BP 神经网络来实现DBN 的网络结构。当各输入参数时间序列为预测t 时刻前1 h，1～2 h 和1～3 h 时，计算得到输入层神经元个分别为5，9 和13。当误差反向传播时，输入层-隐含层、隐含层-隐含层和隐含层-输出层的传递函数选取Log-Sigmold 函数，即f(x)=1/(1+e-x) 。经过大量试算，确定隐含层神经元个数取为6，预训学习率为0.8，微调学习率为0.001，预训最大迭代数为300，微调最大迭代数为2000。

3 分析及讨论

如图2～4 分别为输入参数时间序列为预测时刻前1 h，1～2 h 和1～3 h 时得到的供热负荷预测值及相对误差。各时间序列下供热负荷相对误差分别在-8.06%～9.08%，-7.57%～12.15%和-7.12%～15.22%之间变化。即输入参数时间序列为预测时刻前1 h 时，供热负荷时相比其他两种情况的相对误差变化幅度较小，预测得到的结果更加稳定。

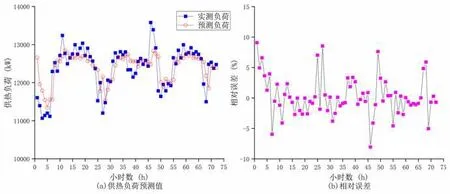
图2 输入参数时间序列为预测时刻前1 h 时供热负荷预测值及相对误差

为对供热负荷的预测精确性进行评价，本文引入平均绝对误差和平均相对误差作为评价模型，计算得到的输入参数时间序列为前1 h，1～2 h 及1～3 h 时各类误差值如表1 所示。当输入参数时间序列取为预测前1 h 时平均绝对误差和平均相对误差分别约277.98 kW 和2.28%，相比输入参数时间序列取为1～2 h 和1～3 h 具有更高的预测精确度。

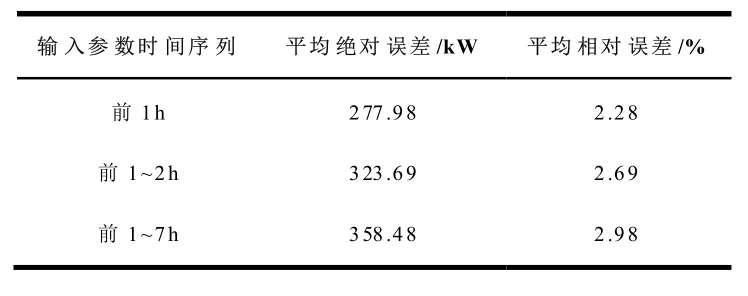
表1 输入参数时间序列为前1 h，1～2 h及1～3 h 时各类误差计算值

图3 输入参数时间序列为预测时刻前1～2 h 时供热负荷预测值及相对误差

为分析DBN 在供热负荷预测领域的优势，采用现阶段常用的预测模型ANN 作为对比对象，如图5为时间序列为预测时刻前1 h 时，各预测模型得到的预测负荷值和相对误差，通过计算得到ANN 的平均相对误差和平均绝对误差分别约为295.54 kW 和2.43%，各误差相比DBN 分别提高约17.56 kW 和0.15%。

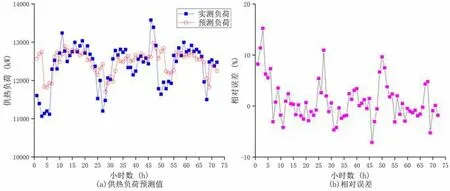
图4 输入参数时间序列为预测时刻前1～3 h 时供热负荷预测值及相对误差

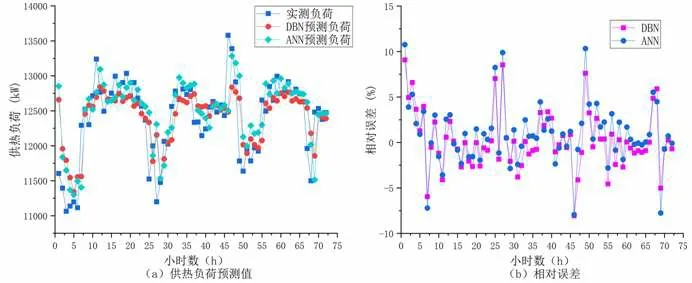
图5 输入参数时间序列为预测时刻前1 h 时DBN 和ANN 供热负荷预测值及相对误差

4 结论

本文采用深度置信网络对区域供热逐时负荷进行预测，并将预测时刻1 h，1～2 h 及1～3 h 作为输入参数的时间序列对预测精度进行分析。结果显示，当输入参数时间序列取为1 h 时，平均相对误差和平均绝对误差分别为277.98 kW 和2.28%。同时，当输入参数时间序列取为1 h 时，DBN 的预测精确度显著优于目前常用的ANN 预测模型。由此可见，深度置信网络在供热负荷预测领域极具应用潜力，未来可对深度置信网络的结构参数取值等方面进行深入研究，以提高其预测精度。