高速土工离心机温升的数值模拟

邵文博，任晓栋，胡博

重大工程装备

高速土工离心机温升的数值模拟

邵文博1，任晓栋2，胡博2

（1.清华大学无锡应用技术研究院，江苏 无锡 214000；2.清华大学 能源与动力工程系 热科学与动力工程教育部重点实验室，北京 100000）

目的数值计算高速土工离心机机室温度分布，研究不同真空度和侧壁温度对机室温升的影响，并为高速土工离心机提出温控方案。方法针对一款在建的高速土工离心机，采用SRF方法和RNG-湍流模型对其进行数值计算，对比不同转速下离心机的温升。针对加速度为1 500的运行工况，对比不同机室压力和侧壁温度对机室温升的影响。结果高速土工离心机以1 500加速度运行时，机室最高温度可达83 ℃。运行压力从100 kPa降至3 kPa，机室最高温度下降约15 ℃，侧壁温度每降低10 ℃，机室最高温度降低约5 ℃。另外，真空度配合侧壁冷却无法满足散热要求时，可考虑在机室顶部靠侧壁布置面积不小于顶部面积1/4的冷却环。结论利用CFD数值计算方法，定量得到了高速土工离心机机室温度随转速、真空度和侧壁温度的变化，为其冷却方案的设计提供了参考。

CFD；SRF；高速土工离心机；风阻功率；温升

土工离心机是土动力学研究的重要物理模型模拟手段，该设备通过转臂高速旋转形成超重力环境，可以准确还原出岩土自重应力条件，用以研究岩土的变形机制和破坏特征，被称为岩土地震工程和土动力学最有效、最先进的科学试验平台[1-4]。由于其在岩土工程和土动力学模拟试验中的优越性，土工离心机受到了各国的重视和发展，近年来都朝着高转速和大容量发展。我国虽然在土工离心机的研制上起步较晚，但随着科技水平和综合国力的提升，我国已建成和正在建设的大型土工离心机达20～30台，主要分布在南京水科院、清华大学、同济大学、中国水科院、成都理工、香港科技大学和浙江大学等单位[5-7]。其中，中国水科院正在建的离心加速度能达到1 000的土工离心机，浙江大学正在建的加速度能达到1 500的高速土工离心机[8]（简称高速机），都将达到世界先进水平。

土工离心机在运行过程中，空气阻力做功会导致机室内温度升高，而过高的机室温度会严重影响机载设备的正常工作，必须配套相应的散热系统，以保证土工离心机始终运行在正常的温度区间[9-10]。若能准确预估土工离心机的产热量，便能设计出相应的散热系统。因此，风阻功率作为土工离心机主要的产热源，近年来得到不少学者的关注。杜延龄等[11]对国外土工离心机风阻功率的估算方式进行了总结，提出了一种风阻功率的计算公式。孙述祖等[12]对比了几种风阻功率公式计算值和实验值的误差，研究了机室空气的温度、湿度对风阻功率的影响，得出了风阻功率与温度的关系。尹益辉等[13-14]研究了通风和密闭环境下转臂对空气的做功方式，总结了通风和密闭条件下，土工离心机风阻功率的计算公式。郝雨等[15]利用CFD数值计算的方法模拟了一款中低速土工离心机的风阻功率，对比试验结果验证了采用CFD方法预测土工离心机风阻功率的可行性。当离心机加速度达到1 000以上时，由于产热量急剧增加，系统对散热的要求更加严苛，只通过预估风阻功率，采用风冷或液冷的方法很难能达到散热的要求，需利用主要影响因素参量法来解决土工离心机产热和散热问题[8,16-17]，即研究土工离心机产热和散热机理，从根源解决系统散热问题。林伟岸等[8]针对加速度为1 500高速机，通过缩比模型试验研究了影响离心机主机室温度的主要因素，提出了侧壁冷却和真空度联合调控的温控方案。郑传祥等[18]通过试验和理论相结合的方法，研究了低真空度下高速机的产热机理，提出了高速机产热的第一热源和第二热源。郭毅楠等[19]利用CFD方法模拟了ZJU400中高速大型土工离心机的运行情况，得到了主机室的温度分布，为数值研究中高速土工离心机的产热和散热提供了思路。

虽然上述学者针对高速土工离心机的产热和散热机理进行了一些研究，并提出了相应的温控方案，但是研究主要在缩比模型上进行，与实际模型存在一定差距。另外，有关高速机机室压力和侧壁温度对温升影响的研究也较少。本文针对一款在建的高速机，利用CFD数值计算方法，首先计算了不同加速度时土工离心机的温升，研究了各加速度下该机型机室能达到的最高度，然后对比计算了加速度为1 500时，不同机室压力和侧壁温度对机室温升的影响，并针对真空度配合侧壁冷却无法满足散热要求的问题提出了相应的温控方案。

1 数学模型

对于满足连续性假设的流体介质，使用纳维–斯托克斯方程（Navier Stokes Equation，N-S 方程）来描述。

连续性方程：

动量方程：

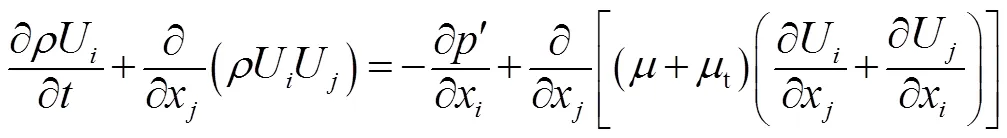
能量方程：

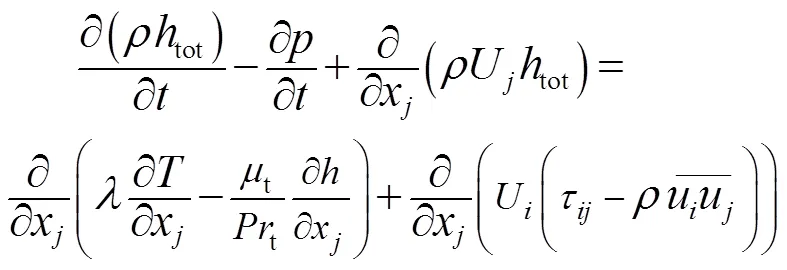
式中：为密度；为热力学压强；U为速度矢量在方向上的分量；动量方程中的为动力黏度；t为涡黏系数（湍流黏度），表示雷诺应力与时均速度梯度的比值；能量方程中tot为平均总焓；为静温；为流体黏性产生的黏性应力张量的分量；t为湍流普朗特数。

湍流模型选用RNG-，湍动能和湍流耗散的运输方程为[20]：

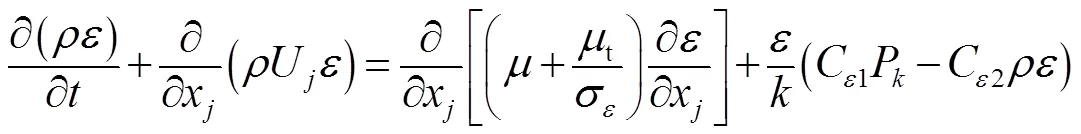
式中：P为黏性引起的湍流产生项；C2=1.68；C=0.085；σ=σ=0.717 9；C1为的函数，见式（6）、（7）[21]。

2 几何模型

2.1 高速机几何模型

为了减少计算量，基于旋转周期假设，本文将高速机物理计算域沿转臂对称面剖分，建立1/2模型，如图1所示。高速机旋转部件由转臂、舱室和转轴组成，舱室位于转臂末端上下两侧。模型保证了高速机主机室的容积、转臂高宽和舱室迎风面积与实际模型一致。各部位尺寸见表1。

图1 高速机计算模型

表1 高速机主要几何尺寸

Tab.1 Main geometric dimensions of high-speed machine m

2.2 网格划分及边界条件设置

网格采用NUMECA Hexpress划分为以六面体为主的非结构混合网格，考虑计算模型为封闭腔体中的换热问题，壁面网格进行加密，并设置10层边界层网格，第1层网格厚度根据经验设置为1×10–5m。整体网格划分如图2所示。网格总数为320万，很多计算表明，该网格尺度满足计算要求。经初步计算，壁面处最大的+值为2.27。

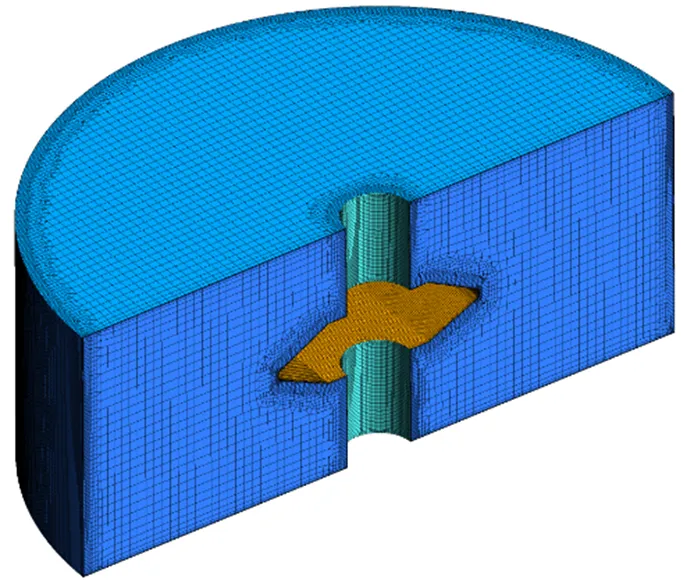
图2 计算域网格划分

数值计算利用CFX 19.0软件，采用单移动参考系（Single Moving Reference Frames，SRF）方法，传热模型选取总能量模型，湍流模型选用RNG-，打开黏性热选项，选择高速壁面传热模型，壁面函数选择Scalable Wall Function。机室侧壁和底部设为等温无滑移壁面，底面温度为298.15 K，侧壁温度按计算工况给定。由于土工离心机产热主要由转臂与空气摩擦和空气与侧壁摩擦2部分组成[18]，转轴和机壁摩擦产热较前2部分产热甚小，在计算中可忽略该部分产热，而且在实际设计中，转轴部分产热会通过冷却系统带走，保证转轴部分不会超温，因此设置转臂和转轴为绝热无滑移壁面。另外，为研究极端情况下离心机的温升，上壁设为绝热无滑移壁面。上下壁面和侧壁面粗糙度均设为0.05 mm，与实际情况保持一致。机室初始温度设为298.15 K，模拟类型设置为稳态，残差标准设定为10–5（RMS）。对流项和湍流项均采用高分辨率差分格式。考虑转臂高转速旋转时空气压缩，打开高速壁面传热模型[High Speed (compressible) Wall Heat Transfer Model]，并选择考虑传热的湍流闭合（Turbulent Flux Closure for Heat Transfer），涡扩散系数设置为0.9。另外，由于低气压环境时，空气物性对计算结果的影响较小，故本文低气压工况均采用常压物性设置，定压比热容、黏性系数和热导率均设置为常数。

3 模型验证

为验证本文数值模型的可靠性，参照尹益辉等[13]对密闭机室型土工离心机风阻功率的研究，建立与文献中一致的离心机模型。离心机机室半径和高度分别为2.6、2.8 m，单侧悬臂最大半径为2.2 m，离心机运转时工作吊斗中心半径和迎风面积分别为2.0 m、0.665 7 m2，单侧阶梯型工作转臂的总长度为1.3 m，宽度为1.2 m，从主轴至吊斗方向，转臂各段尺寸见表2。利用上述方法划分网格，考虑到转臂各段存在一定的厚度变化，除各壁面外，对转臂各段网格再进行局部加密。计算域网格总数为364万，旋转部件和计算域网格如图3所示。

表2 转臂各段尺寸

Tab.2 Dimensions of each segment of the boom m

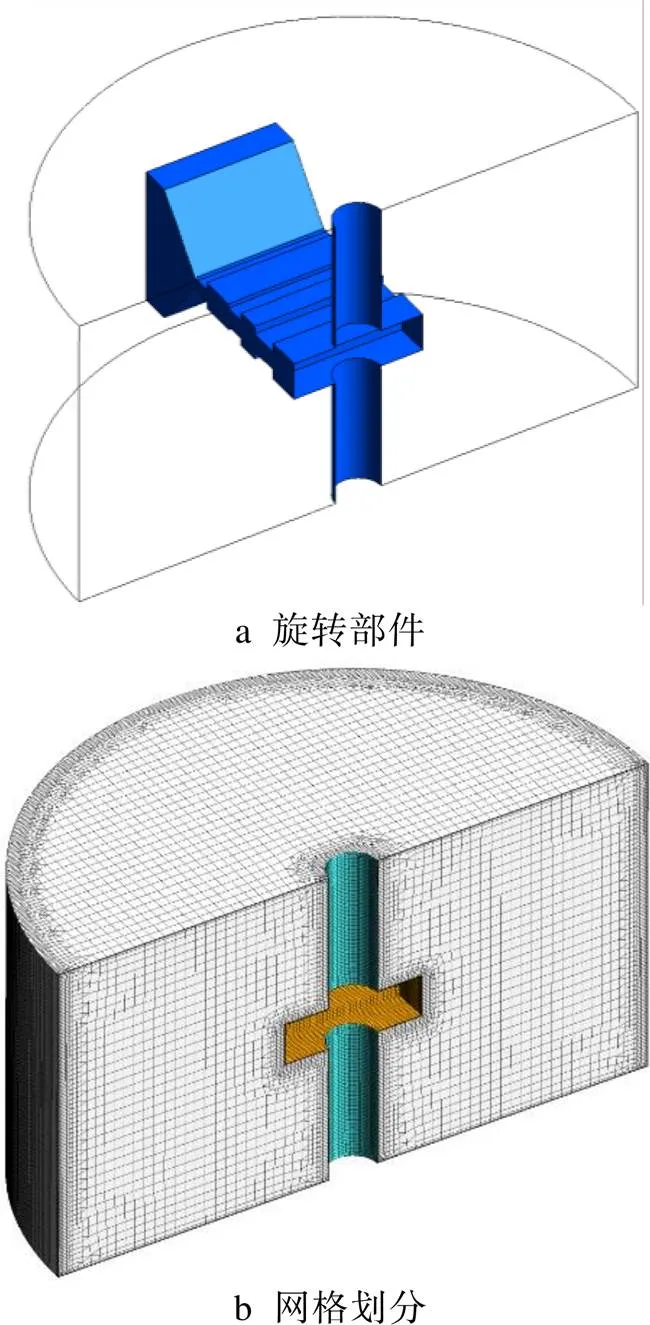
图3 验证模型及其网格划分

4种转速工况下计算所得风阻力矩和试验结果对比如图4所示。离心机以较低转速运行时，转臂和支座间摩擦阻力做功的占比较大[13]。由于计算时并未考虑这部分做功，因此低转速工况下CFD预测值略小于试验值。另外，考虑到建立的简化模型和实际模型存在一定偏差，10%以内的误差可以说明CFD计算的可靠性。综合对比各转速下的误差结果，除转速为15.7 rad/s时的误差为12.5%外，其他转速下的误差均在10%以内，说明常压下建立的数值模型可以较好地预测土工离心机的风阻功率。低压工况运行时，由于空气物性对计算结果的影响较小，故采用常压时的设置，具体见2.2边界条件设置。

图4 不同转速下风阻力矩对比

4 计算结果

4.1 转速对机室温升的影响

土工离心机转速提高，空气阻力做功增大，导致机室内空气温度迅速升高。根据现有的土工离心机风阻功率估算公式，风阻功率和转速的3次方成正比。为进一步研究不同转速下离心机机室温升和产热的原因，本文以建立的高速机模型为研究对象，分别计算加速度为300、600、900、1 200和1 500等5种加速度下高速机的风阻功率和机室温升，分析机室内流场和温度场分布及转速对机室温升的影响。

高速机加速度为1 500、运行压力为100 kPa、侧壁温度为25 ℃时，机室中心水平截面的温度分布如图5所示。转臂逆时针高速旋转带动室内空气一起旋转，旋转空气和侧壁摩擦做功，导致侧壁附近温度较高。在转臂前缘背风面侧，空气流过前缘最高点（图5中a点）后，会出现较大的流动分离。受压力分布的影响，分离区存在一股靠近转臂前缘的回流，部分气流运动至图5中b点后，混入流经间隙的主流，部分在分离区做旋转运动。受回流和旋流的影响，分离区温度较高。

图5 机室中心水平截面温度分布

转臂纵向截面的温度分布如图6所示。由于本文设置上壁为绝热壁面，产生的热量无法从上壁传出，因此机室上半部分靠近转轴区域的温度较高。另外，由于间隙内空气阻力做功较大，间隙内空气温度也较高。其他转速下，机室内空气的温度分布与该工况下基本一致。

图6 转臂纵向截面温度分布

转臂及舱室表面的温度分布如图7所示。由于转臂前缘和侧壁的间隙较小，间隙内流体性能变化剧烈，转臂受到的压差阻力和摩擦阻力较大，阻力做功加剧了机室内转臂旋转耗功，提升了外界能量输入，最终转化为热能，导致转臂温度升高。由于转臂线速度随旋转半径的增大而增大，使得表面温度呈现由内向外逐渐升高的分布。

图7 转臂及舱室表面温度分布

为分析机室中心水平截面的温度分布，本文提取了该截面垂直转臂的一条半径上（即图5中线-）的空气温度，如图8所示。空气温度沿半径方向逐渐升高，由于靠近机室侧壁附近的空气和侧壁存在对流换热，因此靠近侧壁处，空气温度有明显回落。相比机室中心，越靠近侧壁，转速引起的温升效应越明显，侧壁处的温降也越明显。对机室内空气温度求平均值可知，加速度为300、600、900、1 200和1 500时，温升分别为1.4、5.7、13.3、24.6、39.5 ℃。

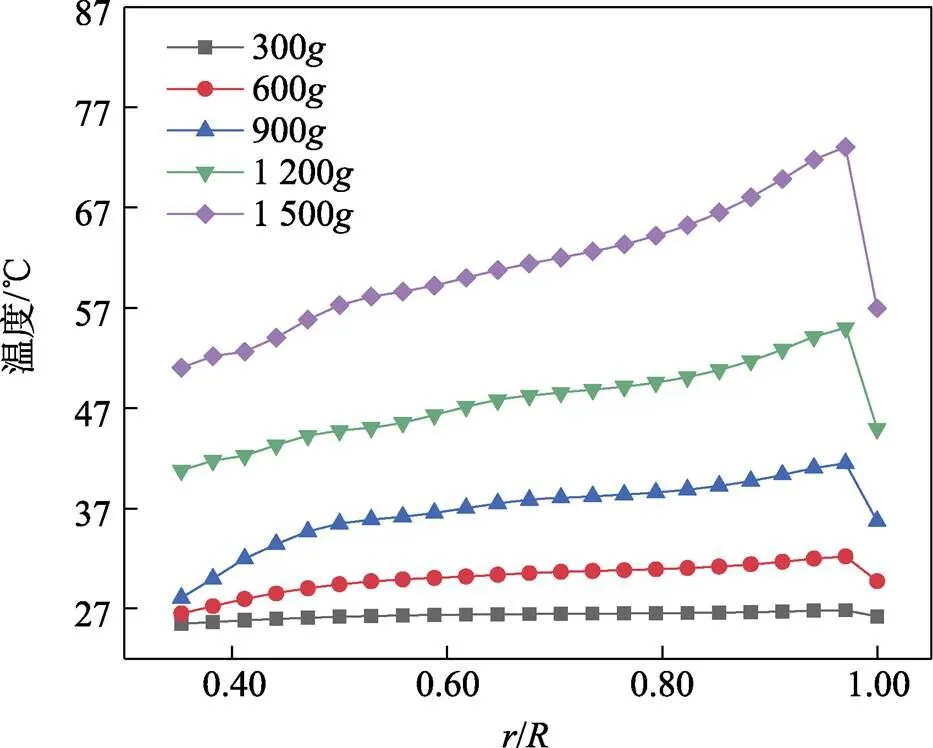
图8 不同转速下线c-c上的温度分布

不同转速下，高速机风阻功率和转臂、舱室表面的最高温度如图9所示。由于机室最高温度和转臂最高温度基本一致，故机室最高温度不再给出，以下所有分析中机室最高温度可参考转臂最高温度。计算所得不同转速下风阻功率和转速的3次方成正比，与现有计算公式中风阻功率和转速的关系一致。转臂表面最高温度基本也和转速的3次方成正比，随转速增大，转臂和舱室最高温度的差值逐渐增大。加速度为1 500时，转臂和舱室的最高温度分别可达83、75 ℃。

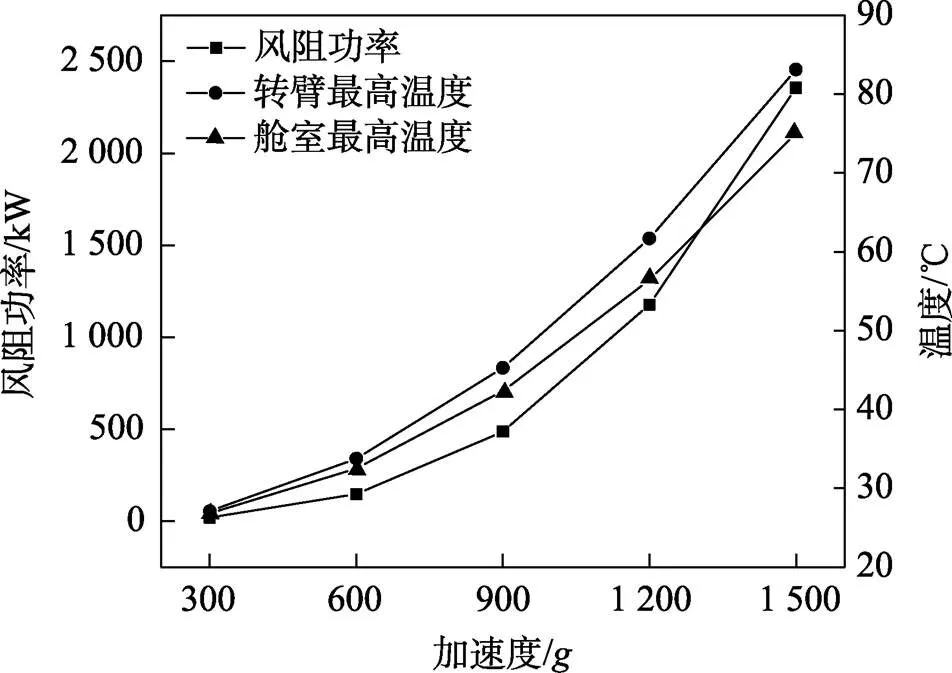
图9 风阻功率和转臂、舱室最高温度随转速的变化

4.2 高速机机室压力对温升的影响

提高主机室真空度是土工离心机用于控制机室温升最有效的方式。高真空度下，空气分子间的距离增大，分子间相互作用减弱，可以有效地从源头上减小产热。随着真空度增加，空气的散热能力也会下降，散热能力随运行气压的非线性变化可能导致机室温度超标[8]。为研究不同真空度下高速机的温升，本文选取加速度为1 500，侧壁温度为25 ℃，分别对绝对压力为100、50、10、5、3 kPa的运行工况进行计算。

不同真空度时，机室中心水平截面半径方向上空气的温度分布如图10所示。由图10可知，降低机室运行气压可有效降低机室内空气温度。当运行气压从1个大气压降至3 kPa时，机室平均气温降低约13 ℃。

图10 不同运行压力下线c-c上的温度分布

风阻功率和转臂、舱室的最高温度随机室压力的变化如图11所示。风阻功率随机室压力下降呈线性下降趋势，绝对压力下降可以有效地降低风阻功率，从而减小产热。不同于风阻功率，转臂表面的最高温度不随机室压力的下降而线性下降。运行气压大于10 kPa时，转臂及舱室最高温度的下降幅度小于风阻功率的下降幅度；运行气压小于10 kPa时，转臂及舱室最高温度的下降幅度大于风阻功率的下降幅度。当运行气压从100 kPa降至3 kPa时，转臂表面的最高温度降低约15 ℃。

图11 风阻功率和转臂、舱室最高温度随机室压力的变化

4.3 高速机侧壁温度对温升的影响

旋转空气摩擦机室侧壁是引起机室温升的主要热源，通过对主机室侧壁降温，可以快速地将热量传递出来，是另一种有效的温控策略[18]。根据上述计算可知，高速机以加速度1 500运行时，降低运行气压至3 kPa，无法将机室温度控制在40 ℃以内，必须采用侧壁冷却配合真空度的温控方式增强散热。

在上述计算的基础上，分别计算了侧壁温度为25、10、0、–10、–20 ℃时高速机的温升，研究高真空度下，侧壁冷却对高速机温升的影响。侧壁温度不同时，线-上的温度分布如图12所示。可以看出，机室温度随侧壁温度的下降逐步降低。侧壁温度越低，侧壁处温度梯度越大，机室的散热能力越强，侧壁附近空气温度的下降越明显。当侧壁温度降低至–20 ℃时，机室平均温度降低约22 ℃。

图12 不同侧壁温度时线c-c上的温度分布

风阻功率和转臂、舱室的最高温度随侧壁温度的变化如图13所示。降低侧壁温度，侧壁附近空气的黏性增强，阻力做功变大，导致高速机风阻功率有微小增加。转臂和舱室表面的最高温度随侧壁温度的降低基本呈现线性下降，侧壁温度降至–20 ℃时，转臂最高温度下降约24.5 ℃。

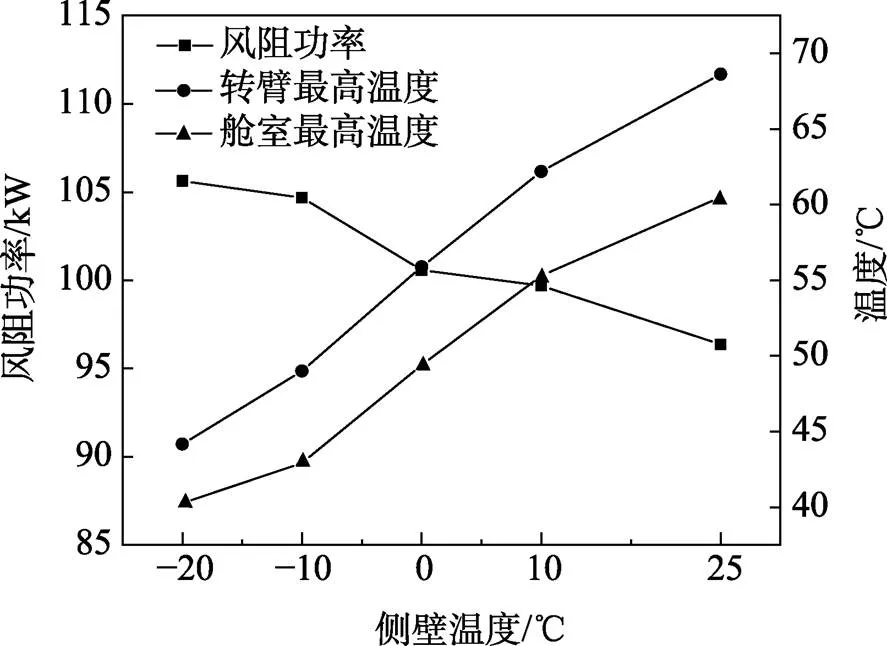
图13 风阻功率和转臂、舱室最高温度随侧壁温度的变化

4.4 上壁冷却环布置方案

根据上述计算可知，高速机在加速度1 500运行时，采用高真空度（3 kPa）联合侧壁冷却（侧壁温度–20 ℃）的温控策略依然无法满足机室温度小于40 ℃的要求。考虑机室侧壁的承压能力和实际制冷情况，进一步降低机室压力和侧壁温度的可行性不高，需在上壁面增加制冷环来增强系统的散热能力。

冷却环布置的4种方案如图14所示，方案1冷却环布置在靠转轴一侧，方案2和方案3冷却环布置在靠侧壁一侧。3种方案中，方案1和方案3冷却环的面积相同，为上壁面积的1/3，方案2冷却环面积为上壁面积的1/4，冷却环温度均设置为–20 ℃。

图14 上壁冷却环布置方案

3种冷却环布置方案下转臂及舱室表面的温度分布如图15所示。相比方案2和方案3，采用方案1布置冷却环时，转臂整体温度较高，转臂前缘高温区增大，进一步说明侧壁附近为主要产热区。冷却环面积从上壁面积的1/4增大至1/3时，除整体温度降低外，上半机室温度的下降也更加明显。

图15 不同方案下转臂及舱室表面的温度分布

3种冷却环布置方案中，线-上空气温度分布如图16所示。采用方案1时，线-上空气温度的分布趋势和不进行上壁冷却时基本一致，都是从机室中心向侧壁，温度逐渐升高。由于冷却环在转轴附近，方案1转轴附近的空气温度为3种方案中最低。方案2在较大半径范围内空气温度基本相同，没有明显的升高趋势，只有在侧壁附近较小区域内有沿半径方向的温度增高变化，说明在靠近侧壁处布置冷却环可以加快机室内热循环，在相同条件下散出更多热量。方案3机室的空气温度分布和方案2相同，由于冷却环面积更大，整个机室温度更低。对比方案1和方案3可以说明，冷却面积相同时，在侧壁附近布置冷却环能更有效地将机室热量传递出来。

图16 不同布置方案下线c-c上的温度分布

3种方案所得转臂、舱室的最高温度和机室平均温度见表3。从表3可以看出，3种方案中，舱室温度均未超出40 ℃，但方案1转臂最高温度为42.1 ℃，说明这样布置冷却环存在机室温度超标的风险。方案2和方案3均能满足高速机运行气温要求，考虑到实际模型的上壁有一定传热能力，出于经济性原则，冷却环面积为上壁面积的1/4即可满足散热需求。

表3 转臂、舱室最高温度和机室平均温度

Tab.3 The maximum temperature of the boom, the cabin and the average temperature of the machine room ℃

5 结论

本文利用建立的数值模型，研究了不同转速下实际高速机模型的风阻功率和机室温升，分析了加速度为1 500时，机室压力和侧壁温度对机室温升的影响，并在真空度配合侧壁冷却无法满足运行温度要求时，对比了3种冷却环布置方案对散热的影响，得出如下结论：

1）高速机在常压不进行侧壁冷却的工况下运行时，加速度达到900，转臂及舱室的最高温度会超出极限运行温度40 ℃。当加速度达到1 500时，转臂的最高温度可达83 ℃。

2）降低机室压力可有效减小风阻做功，减小产热，但室温下降和风阻功率下降是非线性的。运行压力从1个大气压降至3 kPa，转臂及舱室的最高温度下降约15 ℃。

3）高真空度运行时，降低侧壁温度，高速机风阻功率有微小增加，但机室温度随侧壁温度下降基本呈现线性下降，侧壁温度每降低10 ℃，转臂及舱室最高温度降低约5 ℃。

4）当真空度配合侧壁冷却的散热方式无法将机室最高温度控制在要求以内时，上壁冷却环布置在靠侧壁附近具有更好的散热效果，且不小于1/4上壁面积的冷却环面积可基本保证机室最高温度不超出40 ℃。

[1] 白冰, 周健. 土工离心模型试验技术的一些进展[J]. 大坝观测与土工测试, 2001(1): 36-39.

BAI Bing, ZHOU Jian. Some Advances in Geotechnical Centrifuge Model Test Technology[J]. Dam Observation and Geotechnical Tests, 2001(1): 36-39.

[2] 包承纲. 土力学的发展和土工离心模拟试验的现状[J]. 岩土力学, 1988, 9(4): 23-30.

BAO Cheng-gang. Development of Soil Mechanics and Present Situation of Centrifugal Modeling Test[J]. Rock and Soil Mechanics, 1988, 9(4): 23-30.

[3] 王永志. 大型动力离心机设计理论与关键技术研究[J]. 国际地震动态, 2014, 44(5): 44-45.

WANG Yong-zhi. Research on Design Theory and Key Technology of Large-Scale Dynamic Centrifuge[J]. Recent Developments in World Seismology, 2014, 44(5): 44-45.

[4] 陈建阳. 大型土工离心机温升控制试验研究[D]. 杭州: 浙江大学, 2020.

CHEN Jian-yang. Experimental Research on Temperature Rise Control of Large Geotechnical Centrifuge[D]. Hangzhou: Zhejiang University, 2020.

[5] 程永辉, 李青云, 饶锡保, 等. 长江科学院土工离心机的应用与发展[J]. 长江科学院院报, 2011, 28(10): 141-147.

CHENG Yong-hui, LI Qing-yun, RAO Xi-bao, et al. Application and Development of Geotechnical Centrifuge in Yangtze River Scientific Research Institute[J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(10): 141-147.

[6] 张俊, 杨志银. 土工离心模型试验的发展与应用[J]. 岩土工程界, 2005(6): 29-30.

ZHANG Jun, YANG Zhi-yin. Development and Application of Geotechnical Centrifugal Model Test[J]. Geological Exploration for Non-Ferrous Metals, 2005(6): 29-30.

[7] 周健, 刘宁. 离心模型试验技术应用的新进展[J]. 上海地质, 2002, 23(1): 52-56.

ZHOU Jian, LIU Ning. The Latest Application of Centrifuge Model Test[J]. Shanghai Geology, 2002, 23(1): 52-56.

[8] 林伟岸, 郑传祥, 蒋建群, 等. 大容量超重力离心机温控缩比模型试验[J]. 浙江大学学报(工学版), 2020, 54(8): 1587-1592.

LIN Wei-an, ZHENG Chuan-xiang, JIANG Jian-qun, et al. Temperature Control Test of Scaled Model of High Capacity Hypergravity Centrifuge[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(8): 1587-1592.

[9] 林伟岸, 陈云敏, 杜尧舜, 等. 高校建设国家重大科技基础设施机制的探索与实践[J]. 实验技术与管理, 2019, 36(4): 250-252.

LIN Wei-an, CHEN Yun-min, DU Yao-shun, et al. Exploration and Practice on Mechanism of Constructing National Major Science and Technology Infrastructure in Colleges and Universities[J]. Experimental Technology and Management, 2019, 36(4): 250-252.

[10] LI Xin-yao, LUO Zhao-yu, LIN Ming, et al. Design and Research of Condition Monitoring and Fault Diagnosis System of Geotechnical Centrifuge[J]. Applied Mechanics and Materials, 2012, 224: 460-465.

[11] 杜延龄. 土工离心模型试验基本原理及其若干基本模拟技术研究[J]. 水利学报, 1993, 24(8): 19-28.

DU Yan-ling. Fundamental Principle and some Modeling Techniques of Geotechnical Centrifugal Model Test[J]. Journal of Hydraulic Engineering, 1993, 24(8): 19-28.

[12] 孙述祖. 土工离心机设计综述(二)[J]. 水利水运科学研究, 1991(2): 219-226.

SUN Shu-zu. Review of Design for Geotechnical Centrifuge(Ⅱ)[J]. Hydro-Science and Engineering, 1991(2): 219-226.

[13] 尹益辉, 余绍蓉, 冯晓军, 等. 密闭机室型土工离心机的风阻功率[J]. 绵阳师范学院学报, 2010, 29(2): 1-5.

YIN Yi-hui, YU Shao-rong, FENG Xiao-jun, et al. Aerodynamic Power of Geotechnical Centrifuges with Closed Chamber[J]. Journal of Mianyang Normal University, 2010, 29(2): 1-5.

[14] 尹益辉, 余绍蓉, 冯晓军, 等. 机室开有通风口的土工离心机的风阻功率[J]. 绵阳师范学院学报, 2010, 29(5): 1-5.

YIN Yi-hui, YU Shao-rong, FENG Xiao-jun, et al. Aerodynamic Power of Geotechnical Centrifuges with Holed Chamber[J]. Journal of Mianyang Normal University, 2010, 29(5): 1-5.

[15] 郝雨, 尹益辉, 万强, 等. 基于CFD的土工离心机风阻及流场特性分析[J]. 装备环境工程, 2018, 15(2): 52-56.

HAO Yu, YIN Yi-hui, WAN Qiang, et al. Wind Resistance and Flow Field Characteristic Analysis of Geotechnical Centrifuges Based on CFD[J]. Equipment Environmental Engineering, 2018, 15(2): 52-56.

[16] SAWADA M, NISHIMOTO S, OKADA T. New Rapid Evaluation for Long-Term Behavior in Deep Geological Repository by Geotechnical Centrifuge—Part 2: Numerical Simulation of Model Tests in Isothermal Condition[J]. Rock Mechanics and Rock Engineering, 2017, 50(1): 159-169.

[17] MITCHELL D, KRISHNAIAH S, SINGH D N. Determination of Thermal Properties of Soils in a Geotechnical Centrifuge[J]. Journal of Testing and Evaluation, 2006, 34(4): 12009.

[18] 郑传祥, 陈建阳, 蒋建群, 等. 低真空度下土工离心机产热机理试验研究[J]. 装备环境工程, 2020, 17(3): 84-88.

ZHENG Chuan-xiang, CHEN Jian-yang, JIANG Jian-qun, et al. Experiment of Heat Generation Mechanism of Geotechnical Centrifuge under Low Vacuum Degrees[J]. Equipment Environmental Engineering, 2020, 17(3): 84-88.

[19] 郭轶楠, 杨毅, 王亚林, 等. 基于ZJU400土工离心机的CFD模拟方法[J]. 装备环境工程, 2020, 17(11): 85-89.

GUO Yi-nan, YANG Yi, WANG Ya-lin, et al. CFD Simulation Method Based on ZJU400 Geotechnical Centrifuge[J]. Equipment Environmental Engineering, 2020, 17(11): 85-89.

[20] LAUNDER B, SPALDING D. Lectures in Mathematical Models of Turbulence[M]. New York : Academic Press, 1972.

[21] ORSZAGS A, Yakhot V, FLANNERYW S, et al. Renormalization Group Modeling and Turbulence Simulations[M]. London: Academic Press, 1993.

Numerical Simulation on Temperature Rise of High-speed Geotechnical Centrifuge

SHAO Wen-bo1, REN Xiao-dong2, HU Bo2

(1. Wuxi Institute of Applied Technology, Tsinghua University, Jiangsu Wuxi 214000, China; 2. Key Laboratory of Thermal Science and Power Engineering, Ministry of Education, Department of Energy and Power Engineering, Tsinghua University, Beijing 100000, China)

The work aims to conduct numerical calculation of the temperature distribution in the machine room of high-speed geotechnical centrifuges, study the effects of different vacuum degree and side wall temperature on the temperature rise of the machine room, and propose a temperature control scheme for high-speed geotechnical centrifuges. In this work, the SRF method and the RNG-turbulence model were adopted to conduct numerical calculation and compare the temperature rise of the centrifuge at different speed. Under the working condition with an acceleration of 1 500, the effects of different machine room temperature and side wall temperature on the temperature rise of the machine room were compared. The results revealed that the maximum temperature in the machine room could reach 83 ℃ when the high-speed geotechnical centrifuge ran at an acceleration of 1 500. The maximum temperature in the machine room dropped by about 15 ℃ when the operating pressure was reduced from 100 kPa to 3 kPa, and every time the temperature of the side wall decreased by 10 ℃, the maximum temperature of the machine room decreased by about 5 ℃. In addition, a cooling ring with an area not less than 1/4 of the top area could be arranged on the top of the machine room against the side wall when the vacuum degree and side wall cooling cannot met the requirements of heat dissipation. Based on CFD numerical calculation method, the changes of machine room temperature of high-speed geotechnical centrifuge with speed, vacuum degree and side wall temperature are quantitatively obtained, providing a reference for design of cooling schemes.

CFD; SRF; high-speed geotechnical centrifuge; wind resistance power; temperature rise

TU415

A

1672-9242(2022)12-0095-09

10.7643/ issn.1672-9242.2022.12.014

2021–08–09；

2021–09–24

2021-08-09；

2021-09-24

国家自然科学基金项目（51806118）

The National Natural Science Foundation of China (51806118)

邵文博（1993—），男，硕士，主要研究方向为旋转机械数值计算与气动热分析。

SHAO Wen-bo (1993-), Male, Master, Research focus: numerical calculation and aero-thermal analysis of rotating machinery.

任晓栋（1985—），男，博士，副教授，主要研究方向为压气机气动热力学和高精度算法。

REN Xiao-dong (1985-), Male, Doctor, Associate professor, Research focus: compressor aerodynamics and thermodynamic research, high-precision algorithm research.

邵文博, 任晓栋, 胡博. 高速土工离心机温升的数值模拟[J]. 装备环境工程, 2022, 19(12): 095-103.

SHAO Wen-bo, REN Xiao-dong, HU Bo. Numerical Simulation on Temperature Rise of High-speed Geotechnical Centrifuge[J]. Equipment Environmental Engineering, 2022, 19(12): 095-103.

责任编辑：刘世忠