基于TSDPSO-SVM的水稻稻瘟病图像识别
2023-01-10杨化龙杜娇娇
路 阳, 杨化龙,4, 陈 宇, 杜娇娇, 管 闯
(1.黑龙江八一农垦大学信息与电气工程学院,黑龙江大庆 163319;2.东北石油大学黑龙江省网络化与智能控制重点实验室,黑龙江大庆 163318;3.南京优玛软件科技有限公司,江苏南京 210000; 4.黑龙江省鸡西市公安局,黑龙江鸡西 158100)
稻瘟病是一种主要危害叶片、茎秆、穗部的水稻全球性重要疾病[1]。稻瘟病会在水稻整个生育周期内造成极大的危害,与纹枯病、白叶枯病并列为世界水稻三大病害[2]。由于近几年持续性的高温、强降雨导致水稻产区暴发局部大面积的稻瘟病时常出现[3]。目前稻瘟病检测的方法相对落后,主要通过植保专家根据当地预报及时到田间检查症状[4-5]。然而我国水稻种植面积大,采用传统的检测方法不仅工作量十分巨大,且需要投入大量的人力物力,费时费力[6-7]。在这种情况下,研发一种高效快速检测水稻稻瘟病的方法,对水稻稻瘟病的防治有着重要意义。支持向量机因其优异的性能和较低的计算成本,在解决数据分类和回归问题方面获得广泛的应用[8-9]。许良凤等针对玉米叶部病害图像的复杂性,提出将自适应加权的多分类器融合支持向量机应用于玉米叶部病害识别[10]。胡玉霞等应用模拟退火算法优化支持向量机参数C和g并应用于粮虫图像识别中,识别速度和识别率提高了3%以上[11]。但是由于支持向量机的分类性能依赖随机选择的初始参数条件[12],因此需要一种更强大的优化算法提升支持向量机的分类性能。粒子群优化算法经过几十年的研究发展,已经成功应用于神经网络训练[13]、函数优化[14]等各种场合。粒子群优化算法是一种基于种群的随机优化算法,它模仿了鸟群和鱼群等生物的觅食行为。本研究提出一种改进的粒子群优化算法——牵引切换延迟粒子群算法(traction switching delayed particle swarm optimization,TSDPSO),该算法使用进化因子和马尔可夫链自适应地调整速度更新模型。利用粒子迭代搜索局部最优和全局最优的延迟信息,根据迭代状态更新当前迭代中粒子的速度来解决粒子群算法局部寻优和收敛过早的问题。首先对原始采集的水稻病害图像进行病斑分割,提取颜色和形状特征主分量,构建病害图像特征数据集,再利用TSDPSO算法获取支持向量机的最优惩罚因子和核函数,最后利用TSDPSO-SVM模型对水稻稻瘟病进行识别诊断。试验结果表明,牵引切换延迟粒子群算法在水稻稻瘟病识别精度和召回时间上优于传统的机器学习方法。
1 支持向量机及粒子群优化算法
1.1 支持向量机
支持向量机(support vector machine,SVM)是一个二元线性分类器,分类问题本质上是找到决策边界,即求解学习样本最大边距超平面[15]。超平面方程为
f(x)=ωTx+b。
(1)
其中:ω表示超平面的法向量;b表示超平面的偏移量。通过引入拉格朗日系数,将目标函数转化为对偶优化问题,即
(2)
拉格朗日系数c是一个惩罚因子,惩罚因子c影响目标函数的损失值,c越大,误差越大。当误差较大时,支持向量机容易出现过拟合。当c过小时,SVM又可能存在欠拟合问题。在线性SVM中转化为最优化问题时求解的公式计算都是以内积形式出现,因为内积的算法复杂度非常大,所以利用核函数取代内积[16]。本研究选用高斯径向基核函数作为核函数,即
(3)
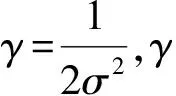
1.2 标准粒子群优化算法
粒子群算法(particle swarm optimization,PSO)是由Kennedy和Eberhart根据鸟群捕食行为提出的一种群体智能优化算法。粒子群算法是由S个粒子组成的群体在D维搜索空间中以一定的速度移动,其中第i个粒子在第k次迭代中产生2个向量,即
vi(k)=[vi1(k),vi2(k),…,viD(k)]和xi1(k)=[xi1(k),xi2(k),…,xiD(k)]。分别为“飞行”速度和矢量位置向量。在迭代过程中,每个粒子的位置会自动向全局最优方向调整,每个粒子自身建立的最佳位置(pbest),用pi=(pi1,pi2,…,piD)表示,整个群体(gbest)中的最佳位置用pg=(pg1,pg2,…,pgD)表示。在找到2个最佳位置后,粒子会再根据公式(4)、公式(5)更新自己的速度和位置。
vi(k+1)=wvi(k)+c1r1{pi(k)-xi(k)+c2r2[pg(k)-xi(k)]};
(4)
xi(k+1)=xi(k)+vi(k+1)。
(5)
其中:w表示惯性权重;c1、c2表示加速度系数;2个随机数r1和r2均匀分布在[0,1]区间。
2 改进粒子群算法
2.1 牵引切换延迟粒子群优化算法
粒子群算法在求解优化函数时有较好的寻优能力,通过迭代,能够迅速找到最优近似解,但容易陷入局部最优,引起较大的误差[17-19]。本研究在借鉴文献[20-21]交换粒子群算法的基础上提出一种新的牵引切换延迟粒子群算法(traction switching delayed particle swarm optimization,TSDPSO),切换延迟的主要思想是根据进化因子和马尔可夫链自适应地调整速度更新模型。利用粒子本身最优位置和粒子种群最优位置的延迟信息,根据迭代状态更新当前迭代中粒子的速度来解决粒子群算法局部寻优和收敛过早的问题。切换延迟粒子群算法的速度和位置更新方程见公式(6)、公式(7)。
vij(k+1)=ω(k)vij(k)+c1[ξ(k)]r1{pij[k-τ(ξ(k))]}-xij+c2[ξ(k)]r2{pgj[k-τ2(ξ(k))]-xij(k)};
(6)
xij(k+1)=xij(k)+vij(k+1)。
(7)
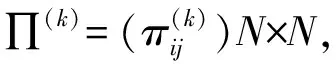
在TSDPSO算法中,通过进化因子对矩阵∏(k)进行自适应调整。根据搜索过程的特点,可以根据进化因子来定义4种状态:收敛、探索、开发、跳出,这4种状态在马尔可夫链中分别用ξ(k)=1、ξ(k)=2、ξ(k)=3、ξ(k)=4表示。群中每个粒子和其他粒子之间的平均距离用di表示。
(8)
式中:S、D分别表示粒子群的大小和尺寸。进化因子Ef定义见公式(9)。
(9)
式中:dg表示平均距离di中的全局最佳粒子;dmax、dmin分别表示di中的最大和最小距离。根据Ef的值,马尔可夫链的状态通过公式(10)确定。
(10)
其中概率转移矩阵见公式(11)。
(11)
因此,下一次迭代时的马尔可夫过程可以基于概率分布矩阵来切换其状态。在迭代过程中,惯性权重w与进化因子Ef具有相同的趋势。较大的w会倾向于在全局搜索中跳出和探索的状态。较小的w则有利于局部搜索。假定将w的初始值设为0.9,描述惯性权重w和Ef的函数见公式(12)。
w(Ef)=0.5Ef+0.4。
(12)
加速度系数c1和c2的初始值设为2,它们都可以根据表1中给出的进化状态自动调整其值。

表1 TSDPSO算法参数设置
2.2 延迟信息的选择策略
TSDPSO利用pbest和gbest的延迟信息,根据进化状态对速度方程进行更新。选择延迟信息的策略:即在跳出状态下,当前全局最优粒子愿意飞到一个更好的解,从而逃离局部最优解。pbest和gbest的延迟信息在搜索空间分布更广。pi{k-τ2[ξ(k)]}和pg{k-τ2[ξ(k)]}是上一次迭代中遇到的粒子和群的最佳位置,它们都包含了粒子和群的信息。因此,选取它们来更新速度方程,有助于跳出局部最优。
在探索状态下,当前迭代中选择pbest和gbest的延迟值可以使粒子单独探索,也可以引导粒子飞到历史上的全局最佳位置。在开发状态下,每个粒子都利用其在当前迭代中的历史最佳位置pi{k-τ2[ξ(k)]}和gbest,以加强对局部的搜索和开发。在收敛状态下,所有粒子都愿意在找到的全局最优区域内尽快收敛到最优解。因此,粒子应该在当前迭代中遵循pbest和gbest,以在该状态下实现目标。
2.3 牵引操作
牵引操作(traction operation,PO)是当粒子陷入适应度值较差的搜索区域时,为了加快粒子群算法的收敛速度,对被困粒子最近10次运动中的最优位置方向执行粒子牵引操作。该操作让粒子能快速离开全局较差区域,让粒子往全局最优解的区域中搜索,以提高粒子搜索速度和算法收敛速度。牵引操作见公式(13)。
PO=c3rand(){pg[k-τ2(ξ(k))]}-pi{k-[ξ(k)]}。
(13)
式中:c3表示自适应牵引因子,定义见公式(14)。
(14)
式中:fi表示粒子i的适应度值;fmin表示种群中适应度最小值;favg表示种群的平均适应度值。自适应牵引因子c3对处于较差搜索区域的粒子影响较大,采用公式(15)进行速度更新。
vi(k+1)=wvi(k)+c1r1[pi(k)-xi(k)]+c2r2{pg(k)-c2r2[pg(k)-xi(k)]}。
(15)
牵引切换延迟粒子群算法优化SVM的流程见图1。

3 TSDPSO-SVM优化算法仿真分析
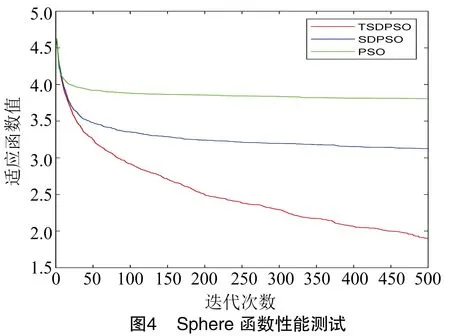
为了验证TSDPSO的性能,选择3种常见的最优化算法性能测试函数Ackley函数、Rosenbrock函数、Sphere函数来评估算法性能。Ackley函数是指数函数叠加余弦函数,寻优过程极易陷入局部极小值;Rosenbrock函数是一个多峰优化函数,在狭窄的波形谷中很难得到最优值;Sphere函数则是典型的单峰优化函数,对优化算法的收敛速度有较好的反映。3种函数表达式分别见公式(16)、(17)、(18)。
(16)
(17)
(18)
本研究同时选取SDPSO和PSO等2种优化算法来测试TSDPSO算法性能,通过对比3个测试函数结果来验证TSDPSO算法优越性。参数设置为:群体样本数S=20,群体维数D=20,最大迭代次数N=500。
3种优化算法对3个测试函数的适应度值分别见图2、图3、图4。其中横坐标表示迭代次数,纵坐标表示适应度值。通过3种测试函数对比,发现TSDPSO算法的鲁棒性最佳,收敛速度最快,寻优能力优于SDPSO和PSO算法。
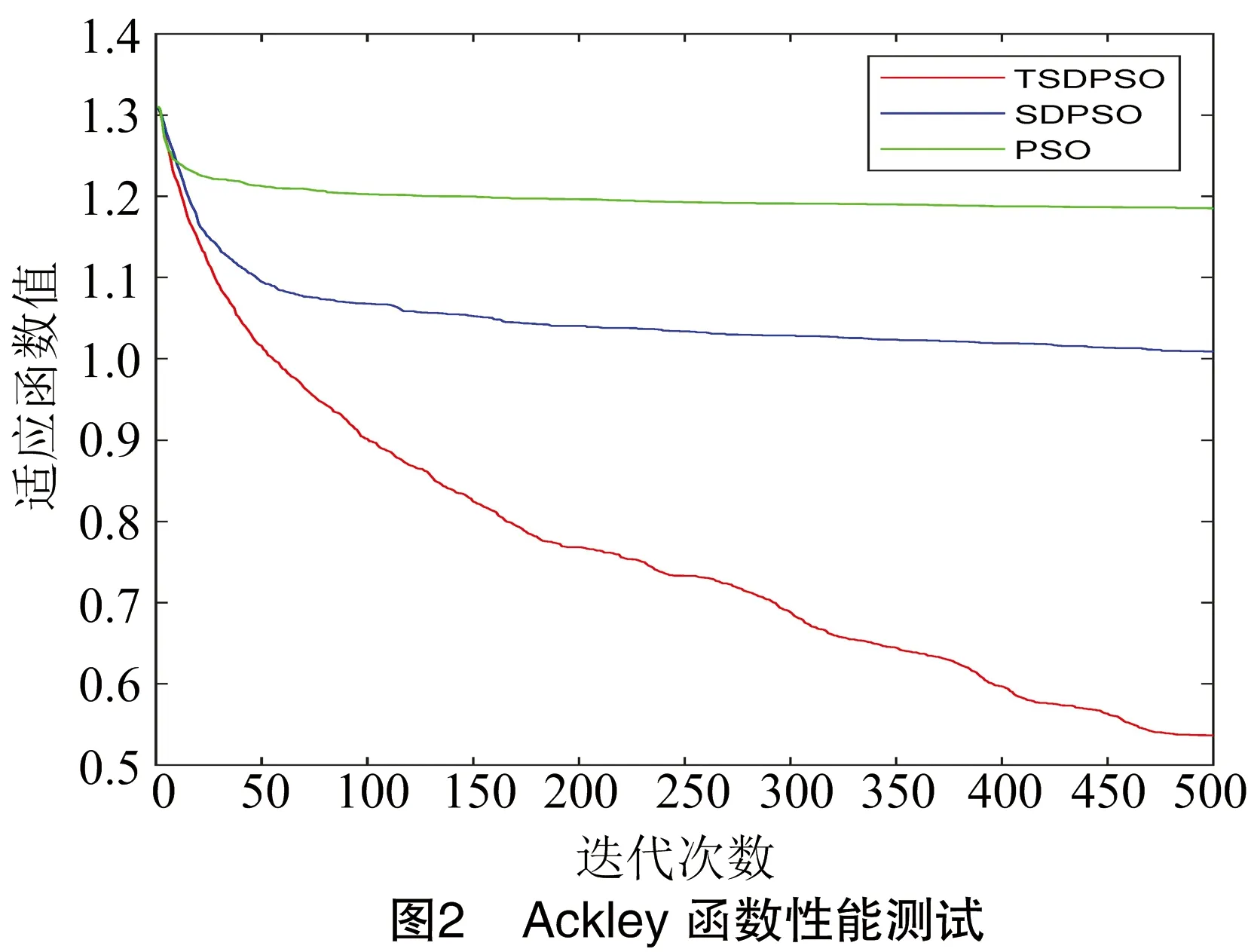
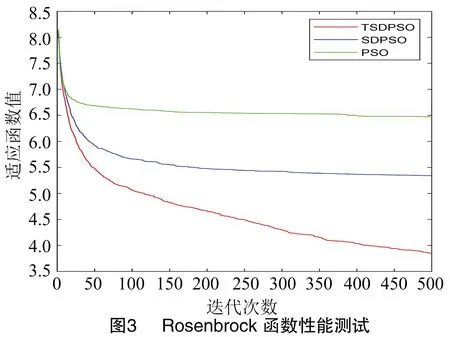
4 基于TSDPSO-SVM的水稻稻瘟病诊断
4.1 水稻稻瘟病图像获取
本研究所用水稻稻瘟病图像于2021年8月从黑龙江八一农垦大学水稻试验田中采集。所有图像均在光线充足的情况下, 使用苹果手机iPhone X(1 200万+1 200万像素双摄像头)对水稻叶部拍摄,拍照时尽量保持图像清晰对焦准确。图像以JPG格式存储,像素为1 312×1 104。由于在拍摄时受各种因素影响,对部分模糊图像采用图像增强等方式处理。健康图像和稻瘟病图像各选取100幅作为数据集,并统一裁剪为28×21大小(图5)。

4.2 水稻稻瘟病图像预处理
由于水稻病斑颜色与背景绿色反差很大,本研究选用基于超绿特征(super green feature)的最大类间方差法(Otsu)对水稻稻瘟病病斑进行分割。通过对超绿图像进行分割,增加绿色通道的权重值,突出绿色分量与病斑颜色分量的对比度。具体操作方法如下:第一,提取水稻稻瘟病R、G、B三色单通道图像,超绿图像见公式(19)。
Y=2G-R-B。
(19)
第二,灰度化处理,任取1个灰度值t1,把该灰度图像分割为主体和其余2个部分。主体的灰度值记为MQ,像素点所占总像素点的比例记为PQ,其余的灰度值记为MS,像素点所占总像素点的比例记为PS。水稻稻瘟病病害图像的平均灰度值记为M。
第三,遍历256个图像灰度级,使用公式(20)计算主体和其余部分的类间方差大小
σ2(t)=PQ(MQ-M)+PS(MS-M)。
(20)
第四,最终输出量为最大方差。最佳阈值为该方差所对应的灰度阈值t。基于超绿特征分割的水稻稻瘟病图像见图6。

4.3 水稻稻瘟病病斑特征提取
4.3.1 颜色特征提取 首先把水稻稻瘟病图像RGB颜色空间转换为HIS和YcbCr颜色空间,再根据归一化直方图计算R、G、B、H、I、S、Y、Cb和Cr的均值、方差、偏度、能量、熵等5个统计特征[22-23]。
4.3.2 形状特征提取 提取水稻稻瘟病病斑的面积、周长、周长直径比、周长长宽比和圆形度5个形状特征。
(1)水稻稻瘟病病斑面积为
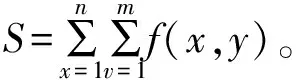
(21)
式中:f(x,y)表示二值图像函数。
(2)病斑周长指病斑区域轮廓长度,用病斑区域中相邻边界点之间的距离和表示。
(3)周长直径比为
(22)
式中:Pc表示病斑周长;De表示病斑的外接圆直径。
(4)周长长宽比为
(23)
式中:Dmax表示病斑最小包围的长;Dmin表示病斑最小包围的宽。最小包围指能够包围图像的最小矩形。
(5)圆形度为
(24)
式中:C取值范围为0~1,C越接近1表示病斑越接近圆形。
通过上述方法提取每幅水稻病害图像的45个颜色特征和5个形状特征,组成一个50维的特征向量。整个数据集共200张图像,总特征数为10 000,计算量大,为了降低维数,快速提取对分类结果影响大、独立、不相关的特征,本研究选取主成分分析法(principal component analysis,PCA)对特征进行降维[24-26]。主成分分析的主要过程如下:第一,采用标准差标准化方法使得所有样本数据分布在[0,1]区间,以消除量纲和数量级的影响。标准差标准化方法见公式(25)。
(25)
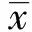
第二,计算协方差。根据协方差定义,标准化特征矩阵x1协方差矩阵Cx的数学描述见公式26。
(26)
式中:n表示向量x1的维数。
第三,计算特征值及对应的特征向量并按特征值降序排列。
第四,计算主成分贡献率及累积贡献率。贡献率ηk和前p个主成分累积贡献率ηp的计算方法见公式(27)。
(27)
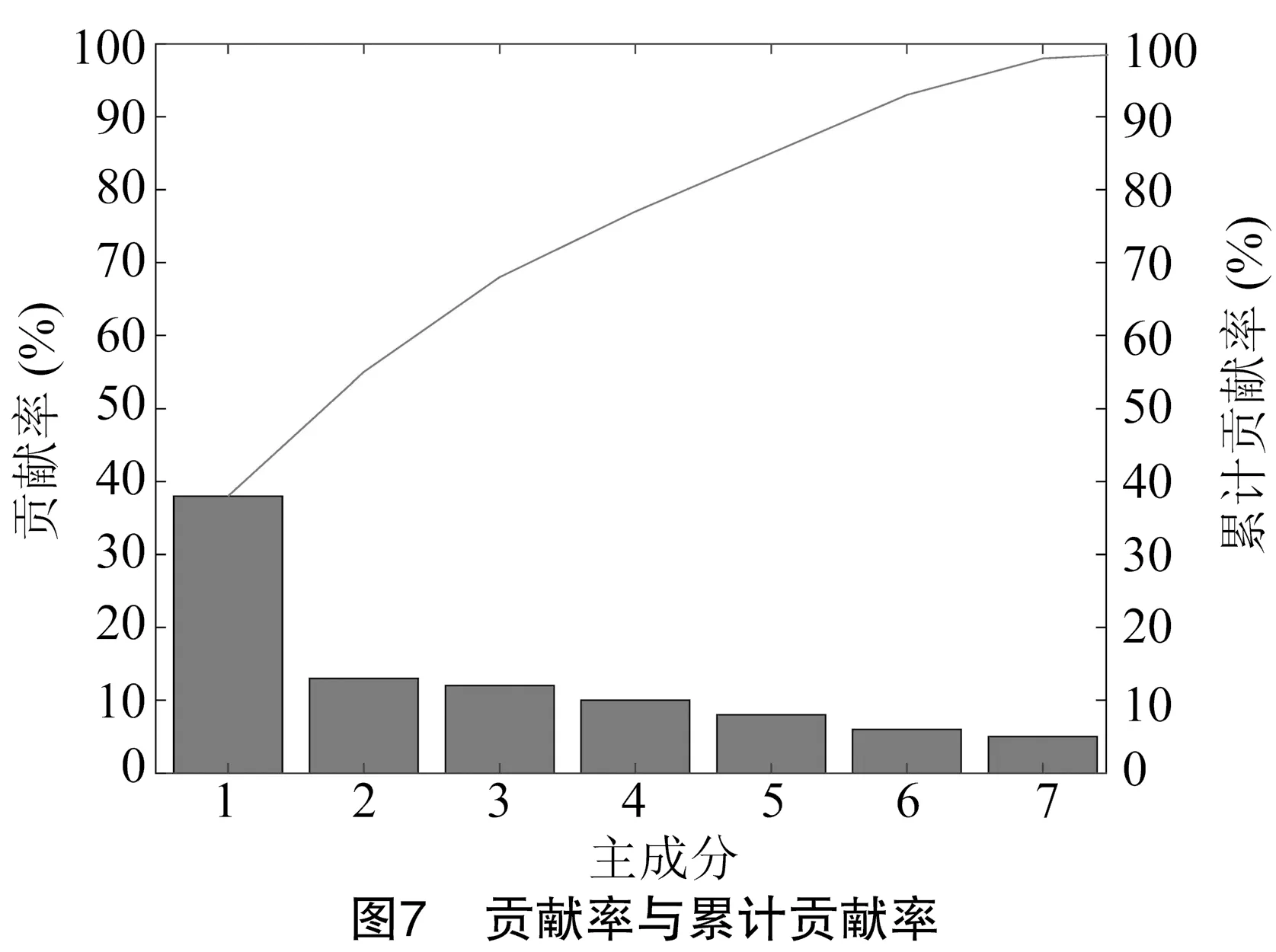
第五,提取主成分。通常选取累计贡献率大于85%的前P个特征值λP对应的特征向量VP组成的P×N的变换矩阵A。根据公式(28)计算得到互不相关的特征向量Y。
(28)
通过对水稻稻瘟病特征矩阵进行主成分分析,主成分的贡献率见图7。
5 试验结果与分析
为了验证所提出方法的有效性,健康叶片和病害图像分别选取70幅作为训练样本,其余30幅作为测试集。对所有水稻稻瘟病图像进行预处理和病斑分割,通过提取病斑图像50个特征值,组成特征向量;训练集组成一个70 50的特征矩阵A,利用PCA过程“分析→降维→因子分析”[27],计算训练集特征矩阵的协方差矩阵,取前M个特征值所对应的特征向量,构成1个50M的映射矩阵B,A×B得到1个70M的低维矩阵C,作为支持向量机训练集数据。本试验使用Matlab2018a软件进行仿真,采用十重交叉验证方法对SDPSO-SVM模型在分类任务中的性能进行评估。为了说明算法的有效性,TSDPSO-SVM分别与SVM、PSO-SVM、SDPSO-SVM3种模型进行准确率(accuracy),精确率(precision)和召回率(recall)对比,3种评价指标分别见公式(29)(30)(31)。
(29)
(30)
(31)
式中:TP表示预测为正的正样本;FP表示预测为正的负样本;TN表示预测为负的负样本;FN表示预测为负的正样本。
由表2可知,本研究提出的方法在水稻稻瘟病识别试验识别准确率指标上达到96.0%,精确率指标达到94%,远高于其他3种模型。召回率指标达到97.5%,虽然与SDPSO-SVM模型持平,但训练时间少了近35 s。综合来看,本研究提出的方法均好于其他研究方法。
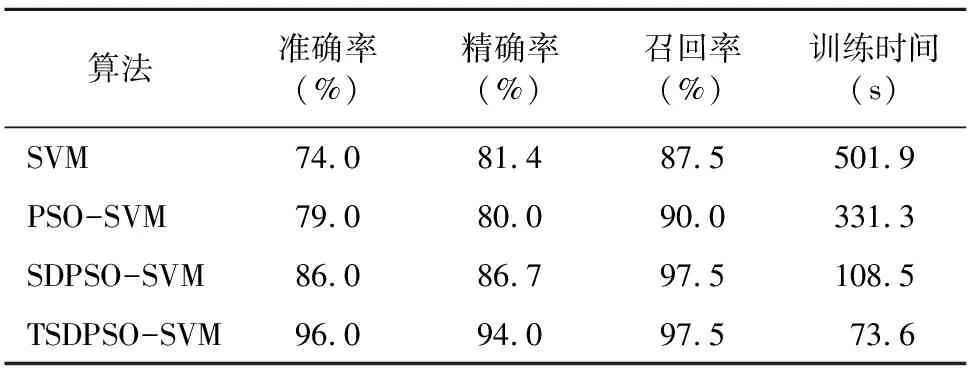
表2 水稻病害识别结果
6 结束语
本研究根据进化因子和马尔可夫链自适应地调整粒子群速度更新模型,提出基于牵引切换延迟粒子群优化算法。选用3种复杂测试函数验证提出的算法全局寻优和全局收敛性能。采用基于超绿特征的最大类间方差法对水稻稻瘟病病斑进行分割,再提取病斑的颜色和形状特征,利用PCA快速得到主分量,构建病害数据库。通过试验验证,发现平均识别率达到96.0%,说明应用TSDPSO优化后的支持向量机对水稻稻瘟病识别取得了较好的效果。与传统的机器学习算法对比,本研究采用的方法在水稻病害识别方面训练速度更快,泛化能力更强,且所需的训练样本数量远远小于深度学习方法,为水稻稻瘟病识别诊断提供了新的思路。
