网格化规划系统中电气计算核心算法的实现

2023-01-10迟福建孙阔张章张媛吴倩

发电技术 2022年6期

迟福建，孙阔，张章，张媛，吴倩*

（1.国网天津市电力公司，天津市河北区 300010；2.天地电研(北京)科技有限公司，北京市昌平区 102206）

0 引言

配电网规划、网损计算、经济调度等都离不开现状电网和规划电网的各种电气计算，包括潮流计算、短路计算、可靠性及N-1校验等[1]。负荷预测是各类电气计算的基础；现状电网的可靠性评估与规划电网的可靠性预测是电气计算的目的，也是实现配电网规划精准投资、精益化管理的要求，需要给出定量的计算结果。

负荷预测方法很多，目前常用的方法大致分为2类[2]：第1类是根据历史用电负荷进行预测；第2类是根据空间负荷密度法直接预测[3]。但目前这2类方法属于空间负荷预测，其结果不能直接用于配电网潮流计算，这是因为配电网潮流和短路计算仅能对有明确数值的电网进行计算，对于负荷集中在地块上的规划电网，算法往往对输入参数要求过高(数量多或者精度高)[4]。目前，能直接用于规划电网电气计算、以馈线为颗粒度的电气负荷预测方法鲜见报道。

关于配电网的N-1校验，目前主流算法是采用深度优先和广度优先的局部拓扑穷举法。这种算法需多次计算，应用起来不够方便。可靠性计算对于现状电网有体系化的成熟公式，但使用时需要较多的输入参数，且数据的获取往往需要估算，不便于工程应用。

针对上述问题，本文提出了网格化规划系统中电气计算的核心算法，并结合德州晶华网格规划项目，将核心算法运用在配电网规划软件中，其计算结果与电力系统潮流计算软件BPA计算结果的误差在8%以内，证明核心算法有效、准确。

1 负荷预测及负荷分配

1.1 负荷预测

1.1.1 近中期负荷预测

近中期负荷预测方法将负荷划分为自然负荷和大用户负荷，全口径最大负荷为自然负荷与大用户负荷之和。

大用户所组成的点负荷是构成电力负荷的重要组成部分，适用于S型曲线。本文对近中期负荷预测进行如下改进：若某些配变的负荷未知，只有容量已知，则配变的负荷大小由式(1)进行估算。

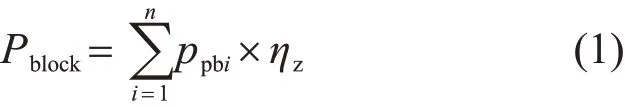
式中：Pblock代表地块负荷；ppbi代表该地块上未知负荷的第i台配变容量；ηz代表该配变所在线路的综合负载率。

各地块的自然增长率按其所属网格最近3年用电的平均增长率来估算今后用电的年增长率，以此来推算规划期的用电负荷。若缺失相关数据，则用户可自行设定缺省值。

1.1.2 远景年负荷预测

采用空间负荷密度法[4]进行远景年负荷预测。对预测区域在空间上进行分区，分为网格、单元、地块3个层级[5]。分区划分存在着包含关系，即供电网格包含供电单元，供电单元包含地块。

应用空间负荷预测法进行预测时，首先结合市政资料确定规划区内每一地块的用地性质及占地面积，再根据确定的各项用地性质负荷指标，计算每一地块饱和负荷[6]。各地块饱和负荷考虑同时率，逐步得到单元、网格总负荷。

当市政资料只有总体性规划时，负荷=地块占地面积×占地面积负荷密度指标；当市政资料有控制性详细规划时，负荷=地块建筑面积×建筑面积负荷密度指标×需用系数。

各类负荷指标的选取应参考各网省公司给出的配电网网格化规划中负荷密度指标的选取原则，并结合实际数据进行类比选取。

1.2 负荷分配

本文所提出的空间负荷分配方法将未来新增地块的负荷转变成线路或变压器的电气负荷。为了体现经济性，避免因解决重载而增加投资成本，本文基于配电变压器经济运行[7]，提出以均衡负荷为目标的配电网规划负荷分配算法，包含地块原有负荷的分配和尚未明确的未来负荷的分配2种情况。均衡负荷是指经优化分配后，各主变、线路负载率相差不多，不会出现明显轻载和重载的情况。

1.2.1 地块原有负荷的分配方法

地块负荷的空间分配如图1所示。地块1的原有负荷1、2、3经开关站KG由馈线1供电，规划年新增负荷1、2计划由馈线1经开关站KG供电，但地块1上未来负荷1、2、3的供电方式未确定。

图1 地块负荷的空间分配Fig.1 Spatial distribution of land load

对于原负荷1、2、3，按照给定的自然增长率(如3%)预测规划年的负荷。对于新增的配电设施——接入新负荷1、2的2台配电变压器，新负荷1、2的负荷取为其所接入配电变压器的容量与配变最优平均负载率(一般取40%~50%)[8]的乘积。

某条馈线规划年已分配负荷计算公式为

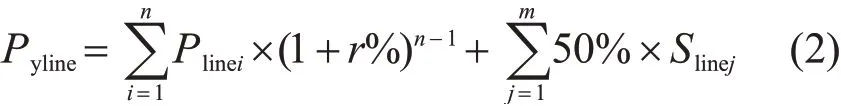
式中：Plinei为该馈线的第i个原有负荷；r%为负荷年自然增长率；Slinej为新增配变j的容量。

1.2.2 地块未来负荷的分配方法

结合图1，假定地块1、2上分别有n条馈线经过，因此这2个地块上的未来负荷可以平均分配在这n条馈线上。实现步骤如下：

1）统计伸入某个地块所有馈线的已分配负荷。对于伸入此地块的每条线段，利用拓扑关系计算其下游接入的所有配变，根据配变经济负载率将配变容量转化为配变负荷，作为该线路的已分配负荷，这样就可以得到每条馈线的已分配负荷，如式(2)所示。

2）计算某地块所有已分配负荷。所有伸入某地块线路的已分配负荷之和记为该地块的已分配负荷，表示为

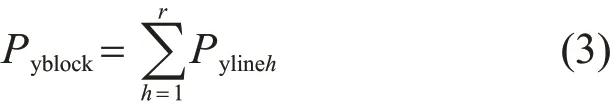
式中：Pyblock为该地块的已分配负荷；Pylineh为馈线h的已分配负荷；r为线路的总条数。

3）计算某地块的未分配负荷。某地块的未分配负荷计算公式为

4）为伸入某地块的每条馈线分配地块的未分配负荷。将地块的未分配负荷分配到伸入该地块的各条线路中，得到每条馈线的未分配负荷，计算公式为

式中：Pulineh为馈线h的未分配负荷；η为所有已分配负荷线路的负载率之和。

现以图1所示地块1中未来负荷1的分配为例对式(5)进行说明。假设一共有r条馈线伸入地块1中，馈线1至馈线m的已分配负荷分别为l1,l2,…,lm，其余r−m条馈线的已分配负荷均为零(为新建馈线)，地块1的总负荷为l0，则地块1的全部已分配负荷为l1+l2+…+lm，则地块1的未分配负荷在馈线1中的分配为

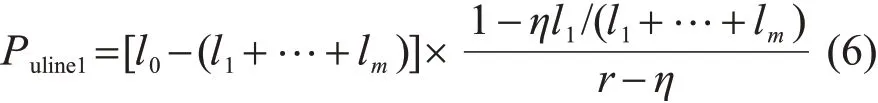
同理，地块1的未分配负荷在馈线m中的分配为

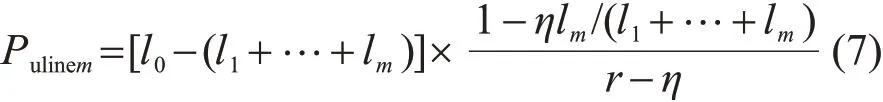
地块1的未分配负荷在新建馈线m+1到r中的分配为

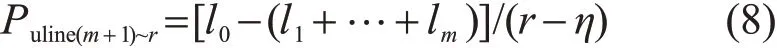
也就是说，将地块1的未分配负荷平均分配到每条新建馈线上；而已分配负荷的馈线则在每条新建馈线分配负荷的基础上，再在各条已分配负荷的线路之间按照自身剩余容量的比例再次进行分配。

这种分配方式考虑了各条馈线之间负荷的均衡性，但也可能会对已有线路造成过载，后续可通过潮流计算、可靠性校验对过载线路进行负荷的二次调整。对线路负荷进行二次调整，就是将重过载线路的某些分支负荷改切到与其相连的联络线路上。假定线路i重过载，线路j,k,…,n与线路i通过联络开关形成联络，线路i有m个分支，即i1,i2,…,im，最优负荷转移步骤如下：

1）首先判断线路j,k,…,n的负载率，按照负载率从小到大的顺序排序，选取负载率最小的线路j为转供线路，将线路i的分支i1,i2,…,im改切至线路j，且保证改切后线路i和线路j均不过载。

2）若线路i的分支i1,i2,…,im改切至线路j后造成线路j重过载，则选取负载率最小的联络线路j和次小的联络线路k共同作为转供线路，按照负荷均衡的原则将线路i的分支i1,i2,…,im均衡改切至线路j和线路k，且保证改切后线路i,j,k均不过载，以此类推。

3）若线路i存在一条超级大分支i1，将i1改切至任意一联络线路上均会导致该联络线重过载，这种情况下可以将超级大分支i1分散为二级分支i11,i12,…,i1p，以二级分支为单位对超级大分支i1进行改切和转供。

4）若线路i经合理转供后线路本身的负载率在合理范围内，但局部分支仍存在重过载时，则考虑线路i是否存在“卡脖子”现象。若有，则将截面小的分支替换为大截面分支；若无，则判定该分支为超级大分支，需要按照步骤3）进一步进行负荷改切，这时可以考虑将该超级大分支的二级分支改切至本线路上，也可改切至其他满足条件的联络线路上。

2 电气一体化算法

2.1 潮流短路合并算法

配电网系统可以用拓扑和潮流完整地表示。拓扑图是对配电网中各条馈线及其电路元件、设备连接关系的数字化描述；潮流是配网中各元件和设备对系统的响应。正常情况下的潮流情况(潮流计算)和故障情况下的潮流情况(短路计算)除需要使用拓扑图外，还需要系统数据、负荷数据以及对各类设备参数的描述数据[9]。因此，需要数据库提供细节支撑数据，如系统电压、有功功率、功率因数，各类设备(架空线、电缆、变压器、电容器)的基本参数，以及各类设备对系统电压、电流、功率的响应方式(对电压、电流、功率因数、负荷、时间或其他因数的响应函数)。

配电网由馈线组成，每条馈线呈树状，馈线间除在根节点处通过高压输电网相连以外，没有其他电气联系，根节点处的电压主要由输电网决定。每条馈线的潮流分布由其本身的负荷及根节点处的电压决定，与其他馈线无关。因此，配电网潮流、短路电流计算可以馈线为单位，多条馈线并行计算。本文采用前推回代法进行潮流和短路电流计算。

为了配合短路电流计算和避免复杂的网络编号，依据网络拓扑结构建立了数据结构，以便利用节点之间的关系快速进行电气计算。节点表包括本节点ID、本节点有功、本节点无功、前一节点ID和后一节点ID。线路表包括本线段ID、本线段首端节点号、本线段末端节点号、本线段电阻和本线段电抗。以图2所示的8节点模型为例进行配电网潮流计算的说明。

图2 潮流计算的8节点算例Fig.2 Power flow calculation example of 8-node

潮流短路合并计算的具体实现过程如下：

1）在馈线表中设置潮流拓扑和可靠性拓扑2个字段，从潮流拓扑字段中读取拓扑信息，生成临时节点表和临时边表，分别如表1、2所示；再通过合并线段对照表和合并配电设施对照表，提取潮流计算所需参数。

表1 潮流临时节点Tab.1 Power flow temporary nodes

2）对节点电压赋初值，Ui(0)=1，其中i=1,2,…,8。需要注意的是，表1的拓扑结构是经过了一次深度优先搜索，形成的层次关系确定了前推后代潮流算法的节点计算顺序。

3）从最末一级负荷节点j(在图2中，j为节点6、7、8)开始，根据节点j有功功率Pj和无功功率Qj，计算流入该节点的支路电流：

式中：Sj为节点j负荷的视在功率；U*j(0)为节点j初始电压的共轭。

4）逐层计算非末梢节点(如节点4、5)的注入电流，根据基尔霍夫电流定律，应等于式(9)中计算的电流与流出的电流之和：

式中：q为非末梢节点号；m为节点i的子节点个数，如对于节点3，父节点i=2，子节点数m=2，子节点g为5,6。

根据式(9)、(10)对网络进行前向遍历，从末节点出发，利用已知的负荷功率逐一计算，即可求得根节点处的电流。

步骤3）、4）在具体实施时，通过降序排序表1，从表尾到表头查询某节点的所有连接边以及对侧节点，累加对侧节点的电流有功分量和电流无功分量作为该节点的电流，同时将所有连接边的下游电流设置为对侧节点的视在电流，进行前推计算。

5）由步骤2）、3）可求出所有支路的电流，利用已知的根节点电压，从根节点向后可顺次求得各个负荷节点的电压：

式中：Zip为父节点i、子节点p所组成支路的阻抗；Ui(1)为第1次迭代计算的i节点电压值；Iip(0)为父节点i、子节点p之间的支路电流初始值。

6）计算各个负荷节点的电压幅值修正量：

7）计算节点电压幅值修正量的最大值，即max[ΔUp(t)]，其中t为迭代次数。

8）判别收敛条件：

若最大电压幅值修正量小于阈值ε，则跳出循环，输出电压计算结果；否则，重复步骤2）—8），直到满足式(13)的条件为止。

9）在得到各个节点的电压、电流后，就可以计算线路潮流和网损，分别表示为：

式中：Uj为节点j的电压；Iij为支路i-j的电流；Zij为支路i-j的阻抗。

10）将表2中计算得到的电压降、损耗汇总，可得到本条馈线的总电压降、总损耗。计算过程中，需将表1中计算得到的电压值、最大电压降、短路电阻和电抗等写入相应表格的对应字段中。

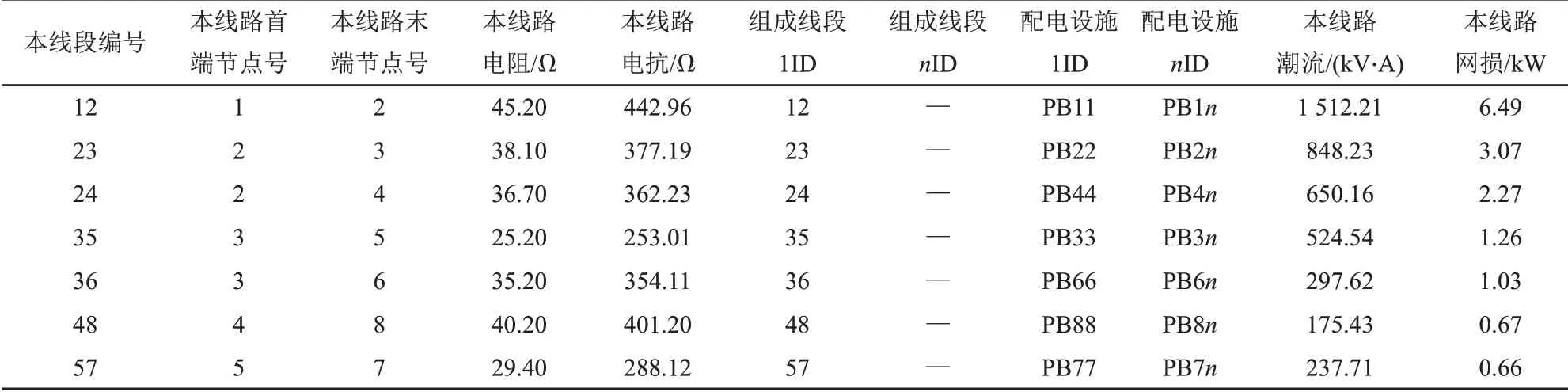
表2 潮流临时边Tab.2 Power flow temporary edges

综上，式(9)、(10)是从末节点出发进行前向遍历，计算各分支电流，式(11)—(15)是从根节点出发进行后向遍历，计算各节点电压，这样就完成一次前推后代的计算。配电网规划中，只需一次前推和后代过程，结果即可满足规划精度要求。

步骤4）—8）在具体实施时，将电源点的短路电阻和短路电抗设置为变电站的短路电抗，将电源点的电压设置为馈线的额定电压。通过升序排序表1，从表头到表尾查询某节点的所有连接边以及对侧节点，将对侧节点电压设置为该节点的电压减去其所连接边的电压降。

同时，为了计算短路电流，将对侧节点短路电阻、电抗设置为该节点的短路电阻、电抗及其所连接边的电阻、电抗之和。需要注意的是，将光伏发电等新能源电源看作是负荷为负值的节点[10-11]。通过后代计算即可得到表2中的电压降，最后在步骤9）计算线路潮流和网损。

2.2 可靠性计算

配电网可靠性最常用的参数是预安排停电时间和故障停电持续时间，其计算过程与潮流计算过程类似，所不同的是，潮流分析中计算的参数是系统各节点的电压和电流。

可靠性评估可以利用潮流计算模型，基于配网系统的拓扑结构，将实际配电网络转化成一个基于设备串并联的可靠性计算网络。串联设备故障率是各设备故障率的累加，任何一台设备故障都会导致整个链条停运；并联设备则存在冗余(根据容量确定)，可以应对其他并联路径的停运。一般而言，并联设备是线路中设置的联络开关。

本文提出的可靠性计算利用潮流计算的表1、2，通过累加线路故障平均停电时间、线路预安排平均停电时间而得到，计算简便，在应用时，只需将式(10)中的电流换成平均停电时间即可，不再赘述。

2.3 N-1校验

N-1校验基于潮流计算结果，用以判断某条馈线或某些配变故障时能否实现负荷的转供[12-15]。根据馈线第1段的下游转供模式能否实现，来判断馈线是否满足N-1校验。具体来说，假定馈线出口的第1段发生故障，则后续所有负荷都需要转供；找出所有联络开关，形成转供后的网络拓扑；通过对转供后网络进行潮流计算，得到该馈线出口第1段的电流。判断该电流值是否超过馈线的额定电流，若超过，则判断不满足N-1校验；否则判断为满足校验。最后，把N-1校验结果写入馈线表对应字段中。

各种电气计算结束后，将各类计算的结果用Excel表格的形式输出。计算结果可分供电单元、供电网格小计，也可全网合计，还可标注重过载线路和低电压线路。

2.4 中压馈线可靠性计算

2.4.1 现状电网中压馈线可靠性估算

本文采用的可靠性指标是年平均故障停电时间和年平均预安排停电时间。假定每户用电平均负荷为1 kW，且忽略双电源的因素，考虑配电自动化安装情况，配电自动化排查故障时间为零，则可得到每条馈线年平均故障停电时间：

式中：Lal为馈线总长度，km；flf为每年每百千米馈线内所有开关、配变等设备的综合故障次数；kp%为配变自动化安装率；1-kp%定义为故障排查系数；tc为故障人工平均排查时间，h；tR为故障平均修复时间，h；Alf定义为故障修复系数，计算公式为

式中：Pi,j为第i条馈线第j段故障情况下本段及下游不可转供负荷之和；Pi为馈线i的总负荷；fi,j为第i条馈线第j段的故障率。

该馈线i的年平均预安排停电时间表示为

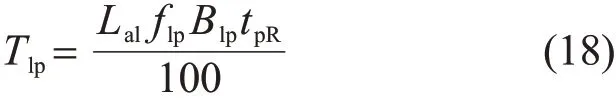
式中：flp为该馈线的故障率；Blp为该馈线的年平均预安排停电转供系数，不考虑开关操作是自动操作还是人工操作时，Blp应与Alf在数值上相等；tpR为预安排故障修复时间。

现状电网的Alf和Blp主要与网架结构有关，可以通过可靠性拓扑计算得到。

2.4.2 规划电网中压馈线可靠性预测可靠性预测具体流程如下：

1）根据现状电网的可靠性网络拓扑结构，求得现状电网的故障修复系数Alf或预安排停电转供系数Blp。

2）将现状电网馈线的实际年平均预安排停电时间Tlp0(下标0代表现状年，下同)、实际馈线平均长度Lal0、实际馈线平均故障率flf0和Blp0代入式(18)，可计算得到现状年预安排停电修复时间tpR0。由于各年预安排停电修复时间变化不大，可将tpR0作为未来规划电网的年预安排停电修复时间tpR。

3）根据规划年电网的可靠性网络拓扑结构，计算得到规划年电网的预安排停电转供系数Blp，代入式(18)，可计算出规划年预安排平均停电时间Tlp。

4）根据现状电网的可靠性网络拓扑结构，求得现状年故障平均停电转供系数Alf0；假定故障修复时间tR与预安排故障修复时间tpR相等，将现状电网的实际年平均故障停电时间Tlf0、实际馈线平均长度Lal0、实际馈线平均故障率flf0、第(2)步中求得的年平均故障修复时间tR、配电自动化安装率kp%代入式(16)，可计算得到现状年故障排查实际时间tc0。由于各年平均故障排查时间变化不大，可将现状年平均故障排查时间tc0作为未来规划年平均故障排查时间tc。

5）根据tR、tc，按照式(16)和(18)计算规划年各年单条线路的年平均故障停电时间和年平均预安排停电时间，即可得到中压配电系统可靠性指标。

综上，可靠性指标的计算只需要已知架空线路和电缆线路的预安排停电次数(概率)、故障停电次数(概率)，再结合网架结构就可以进行可靠性评估与预测。需要注意的是，开关和配变的预安排停电概率和故障停电概率已经折算到其所在的线路上。

架空和电缆线路故障停电次数(概率)的确定原则如下：对于网架结构提升类项目，其可靠性的提升体现在网架结构的改善上，意味着可靠性拓扑计算中Alf值的降低，可根据规划电网可靠性拓扑图求得；对于设备改造类项目，其可靠性的提升体现在设备故障率的降低上，意味着可靠性拓扑计算中flf值的降低。高故障率设备的改造项目在计算改造后的可靠性指标时，应适当调低设备的故障概率。

架空和电缆线路预安排停电次数(概率)的确定原则如下：预安排停电概率的预测应该根据综合停电管理、不停电作业计划和规程进行综合确定。

3 算例分析

以德州晶华网格为例，选取2020年网格内所有10 kV中压线路进行潮流、可靠性计算，并进行N-1校验，计算结果如图3所示。各条线路的计算结果如表3所示。

表3 线路计算结果Tab.3 Line calculation results

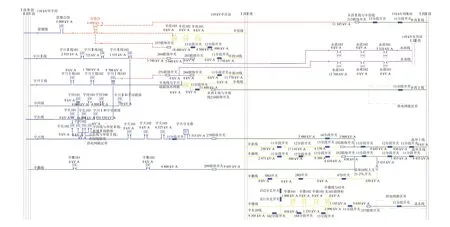
图3 晶华网格10 kV馈线电气一体化计算结果Fig.3 Electrical integration calculation results of 10 kV lines of JingHua network

对国网德州供电公司城市电网规划河东区晶华网格2020年10 kV规划电网进行电气计算，整个网格包含23条馈线(其中3条为区外线路)，计算用时仅1.8 s。将本文的电气计算结果与电力系统潮流计算软件BPA计算结果进行对比，二者误差在8%以内，符合工程要求，这表明本文提出的算法具有准确性、快速性和合理性。