均匀设计法在淤泥刚度参数确定中的应用
2023-01-09张智恒庞小朝
张智恒 庞小朝
铁科院(深圳)研究设计院有限公司,广东 深圳 518060
城市发展过程中,基坑工程不断增多,对基坑安全性提出了更高要求。基坑安全涉及基坑在开挖过程中支护结构横向变形的发展,而横向变形与土层信息及土体的主要刚度参数(参考割线模量Eref50、参考切线模量Erefoed、参考卸载再加载模量Erefur)有关。根据相关理论基础和工程经验,硬化土本构(Hardening Soil,HS)模型是反映基坑支护结构横向变形的常用土体本构模型,把加载变形和卸载变形有所区分,体现了土体的应力-应变关系和土体的剪胀性。在HS模型基础上通过有限元数值仿真、室内土工试验或合理参数反演手段得到土体的主要刚度参数。均匀设计法是一种参数反演分析方法,其本质是通过数论中一致分布理论对区间范围内参数进行均匀筛选,取方差最小的参数或参数组合为待反演的参数或参数组合。杨兰强等[1]通过室内土工试验得到土体应力-应变关系,根据模拟曲线确定了宁波地区典型土层的HS模型参数及其关系,验证了HS模型及试验获取HS参数在基坑开挖数值计算中的适用性。刘书斌等[2]在对硬化土模型及模型参数进行理论分析的基础上,基于室内不同应力路径试验,确定了无锡地区典型土层HS参数,通过Z_Soil有限元数值模拟对比了基坑围护结构水平位移的计算值和实际测量值,表明土体的最大水平位移出现的区域相近,且计算值与实际测量值误差较小,符合反演要求。王卫东等[3]通过大量室内三轴试验确定了土体各土层的本构模型参数,并确定了3个主要刚度参数与压缩模量之间的比例关系,分析结果在上海软土地区基坑工程应用中具有可靠性。刘畅[4]用HS模型进行有限元数值仿真,把土体的3个主要刚度参数与压缩模量的关系进行了对比和拟合分析,反演得到的参数取值对于天津软土地区HS模型的主要参数选取具有参考借鉴意义。刘关虎[5]结合珠海地区淤泥土层基坑工程,采用均匀设计法与Plaxis2D有限元软件计算结合的方法,对淤泥土层的3个未知刚度参数进行反演分析,验证了拟合参数的合理性。
深圳地区存在较多的淤泥土层,本文结合深圳地铁12号线和平站基坑工程,土体本构模型选用HS模型,采用Plaxis2D有限元软件建立仿真模型并结合均匀设计法对淤泥的未知参数进行反演分析。
1 HS模型
HS模型(图1)相比其他模型,在有限元数值模拟中得到的围护结构土体位移较为合理,其弹性部分合理地实现了加载和卸载模量的分别定义,塑性部分则采用了各向同性硬化准则和非相关联流动法则,并在此基础上满足摩尔-库伦破坏准则,在黏土和软土地区有较大的发挥空间。

图1 主应力空间中的HS模型屈服面
HS模型中刚度参数源于标准三轴排水试验的双曲线应力-应变关系(图2)。HS模型共有11个参数,根据Plaxis2D可按以下标准取值:对于砂土,剪胀角ψ可取为φ-30°,对于黏土一般取0°,本次参数反演分析中淤泥土层也取0°;刚度应力水平相关幂指数m对于不同的土体稍有区分,本次分析m值取1;模量参考应力pref则按照理论定义取100 kPa;卸载再加载泊松比vur在Plaxis2D软件中一般取0.2;静止侧压力系数K0根据公式K0=1-sinφ'确定,φ'为土的参考内摩擦角;在Plaxis2D软件中Rf一般默认为0.9。模型3个刚度模量参数通过本次参数反演分析方法结合现场实测值反演确定。

图2 三轴固结排水试验中双曲线应力-应变关系
HS模型中土的极限应力状态是由土的黏聚力c、内摩擦角φ及剪胀角ψ来简化描述。不同的是,HS模型采用三个不同的输入刚度可将土体刚度和土体变形描述得更为精确,从而使基坑开挖工程中的安全性更有保障。
2 均匀设计法
均匀设计法来源于数论中的一致分布理论,即所要反演的因素有若干个,有x个水平的试验可供每个因素挑取。反演过程中,其选取的试验点仅有x个,再通过x个试验点和已知条件对比分析选取最符合反演结果的一组数据。均匀设计法在试验次数相同或相近的情况下,将原来的试验次数从x2次减少到x次,大幅优化了参数筛选程序;由于所选的点在对应的参数区间里呈均匀分散分布,极大限度保证所选的点具有代表性和科学性。
均匀设计有特定的评价指标,一般通过查均匀设计表获得均匀设计方法。每个均匀设计表是通过Un(nm)来体现,其中U表示均匀设计;n为试验次数;m为最大因素数量,即要反演的因素数量。如U7(74)代表4因素7水平的均匀设计表,即有4个参数要反演,一共经历7次试验。本次均匀设计法进行位移反演分析的本质是寻找一组待反演的参数,通过将所得参数代入到有限元软件进行数值仿真,使计算结果的位移值与实测位移逼近即可。目标函数F()
X为

式中:X为待反演的岩体参数;fi(X)为土体在第i个量测点对应的围护结构土体位移计算值;ui为相应的位移量的实测值;k为测点总数。
3 参数反演分析
3.1 工程概况
深圳地铁12号线和平站基坑工程(图3)位于松福大道与桥和路交叉路口,和平站沿桥和路下方呈东西向敷设,途经建筑密集,与正在施工的穗莞深城际铁路(高架)换乘,下穿穗莞深段净高为14.1~14.6 m。车站为地下两层12 m岛式车站,全长230.5 m,标准段宽度为21.1 m,基坑深度16.8~18.7 m,下穿穗莞深城际铁路段用1道混凝土支撑+4道伺服钢支撑。
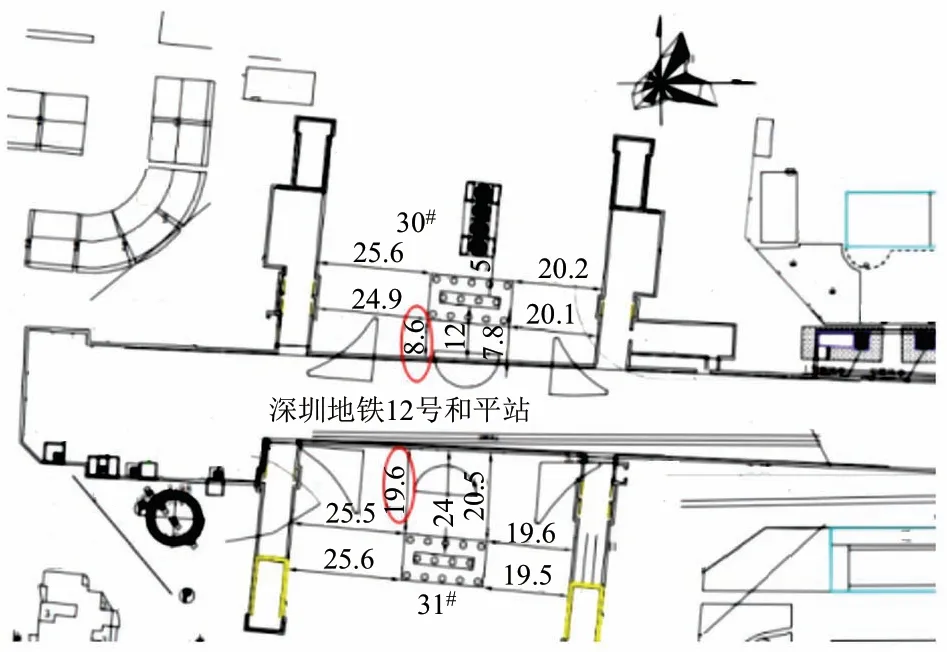
图3 和平站平面示意
本工程中淤泥一般为灰黑、深灰等色,饱和,流塑。淤泥土层较厚,平均层厚9.1 m,而基坑深度在16.8~18.7 m,淤泥占比50%,远超其他土层的层厚占比,因此通过本次有限元数值模拟与均匀设计法相结合反演的基坑工程土体刚度参数近似等于该地区淤泥土层的刚度参数。
3.2 Plaxis2D建模
模型(图4)边界长76 m、宽36 m,模型取车站区间含有伺服钢支撑的基坑部分,基坑侧壁有1道混凝土支撑和4道伺服钢支撑。地连墙厚度1.2 m,抗拉刚度为3.6×107N,抗弯刚度为4.32×106Pa,抗扭截面系数为8 mm3,泊松比为0.15。混凝土支撑深度为0.5 m,第1道伺服钢支撑在基坑中的深度为4.5 m,每道伺服钢支撑间距为3.0 m。混凝土支撑在模型中用锚杆模拟,伺服钢支撑的轴力在模型中用点荷载来模拟,轴力伺服系统的实现是依靠有限元模型中随着土层的开挖地连墙上点荷载逐渐变化来实现的。案例分析中基坑土体为层状分布,淤泥土层分布在上层,层厚9.1 m,深度为4.0~13.1 m,淤泥土体采用HS模型,其黏聚力为10 kPa,内摩擦角为3°。其他土体除素填土采用摩尔-库伦模型之外,均采用HS模型。其他土层参数的取值根据铁科院(深圳)研究设计院多年对于深圳地区土层的参数反演经验取值得到,土层参考应力100 kPa,泊松比为0.2,见表1。

图4 基坑建模Plaxis2D模型(单位:m)

表1 土体HS模型未参与反演的参数取值
3.3 刚度参数均匀设计及有限元计算
采用均匀设计法(UD)与Plaxis2D软件计算相结合方法对基坑淤泥土层硬化土模型主要刚度参数进行参数反演分析。根据相关工程经验及地质勘察资料可确定3个未知刚度参数的取值范围为:。为使参数反演数据更加均匀合理,取均匀设计表U37(3712)来确定具体试验设计方案,然后根据其对应的使用表来安排有限元计算,并输入本构参数进行计算。根据均匀设计表原理,选择U37中列号为1、5、8的列为3个未知刚度参数的均匀设计方案,均匀度偏差最小,具有代表性和合理性,见表2和表3。
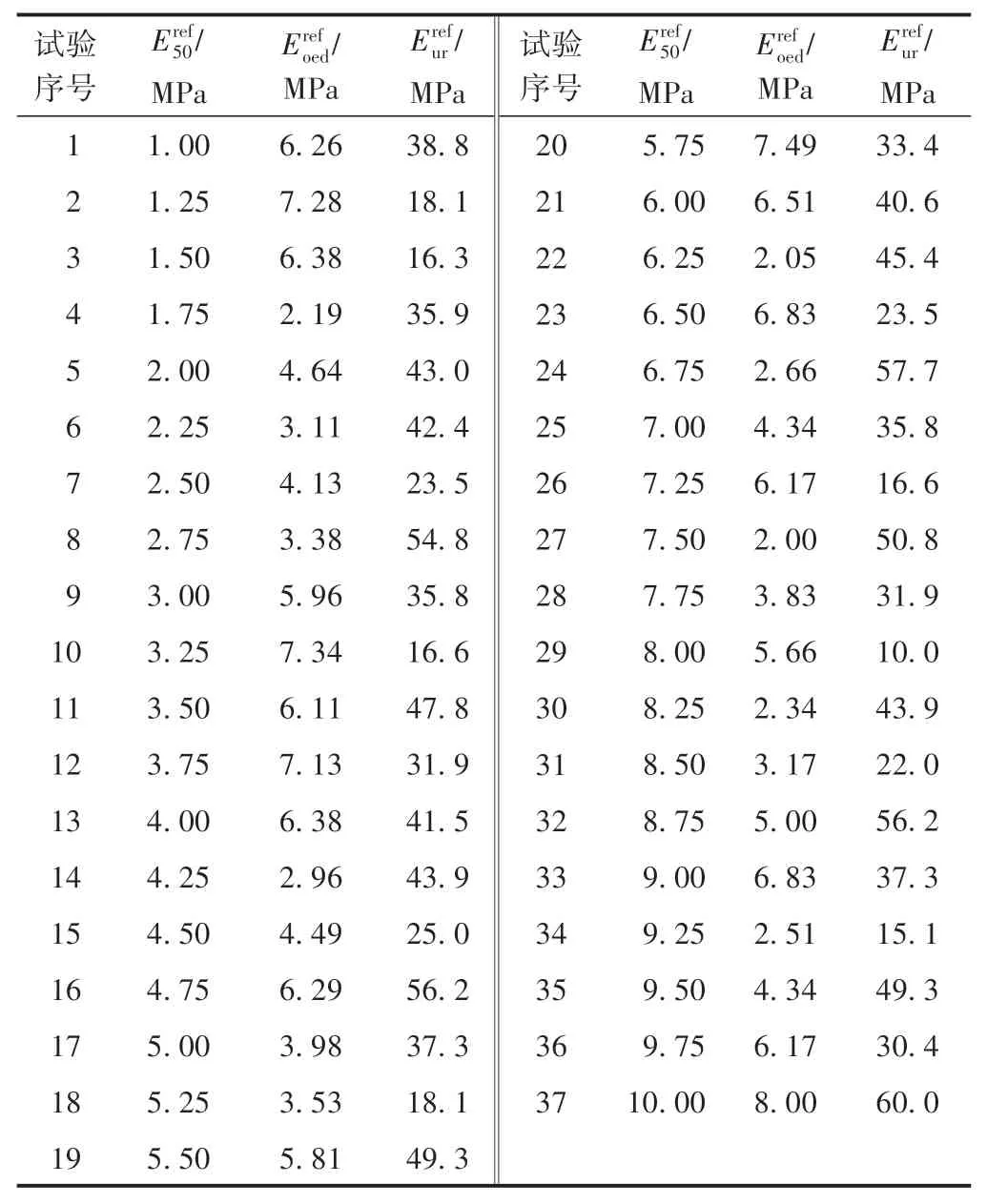
表2 3个未知刚度参数的均匀设计方案

表3 均匀设计表U37(3712)的均匀度偏差D
将表2中可能成立的组合数据代入Plaxis2D有限元软件中进行计算,对比分析基坑地连墙水平位移的计算值与工程现场实测值,观察模型结构深度为4.0~13.1 m淤泥土层区间的地连墙水平位移,计算值与实测值最相近的一组参数组合视为反演出的主要刚度参数。经计算,取=40.6 MPa时,位移最大值与现场实测位移最大值相差最小,见图5及表4。

图5 不同测点的位移
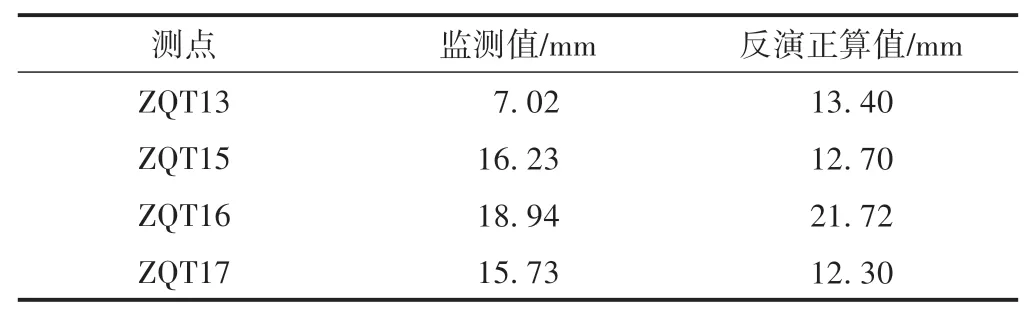
表4 测点位移监测值与反演正算值对比
由表4可知,位移监测值与反演正算值在测点ZQT15—ZQT17差距不大,均小于3.6 mm,且这三处测点的淤泥土层厚度均超过5 m,淤泥土层对地连墙水平位移的影响最大。测点ZQT13的位移监测值与正算值差距达到6 mm,基于该测点淤泥土层厚度仅为3 m,因此实际反演影响不大,反演出的淤泥土层的3个未知刚度参数具有有效性。将计算值与实测值对比曲线中数据代入式(1)计算得到F(X)=72.66 mm2,整体差距较小,计算结果比较吻合。
Atkinson[6]通过测量剪切波速度得到土体在小应变下的刚度参数,并给出了土体刚度参数与土体强度指标的试验规律。根据和平站淤泥土层十字板剪切试验结果和反演得到的淤泥土层三个刚度参数(表5)对比可知,随着深度的增加,原状土和重塑土的抗剪强度逐渐增加;MLZ3-SHP-15试验点埋深4.5~7.5 m为淤泥土层,且其顶层为土体抗剪强度的最小值,底层为土体抗剪强度的最大值。由此可推导与抗剪强度cu之间的大致关系为

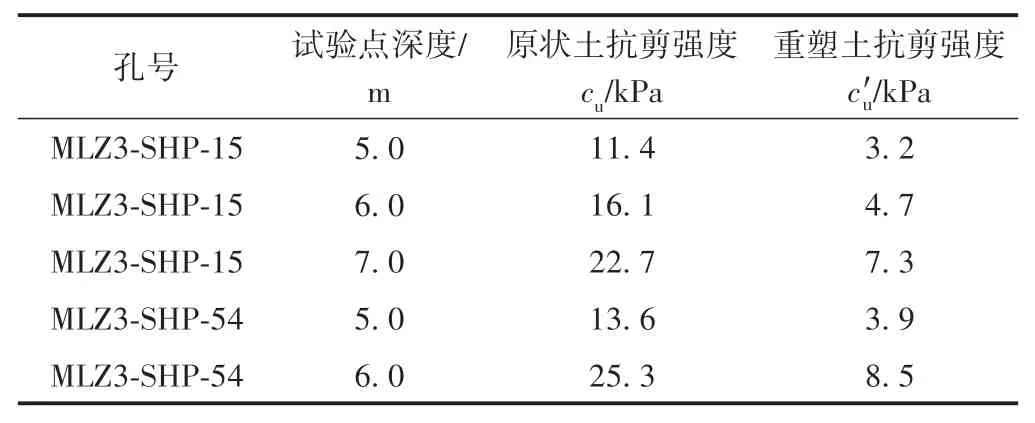
表5 十字板剪切试验结果
根据和平站标准贯入试验成果表可以得到淤泥土层标准贯入击数N最大值为2.0、最小值为1.0、平均值为1.1;不同测点对应的淤泥标贯击数随着淤泥层深度的变化基本保持稳定。由此可以推导与标准贯入击数N之间的一般关系公式为

4 结论
1)Plaxis2D有限元软件计算值与实测值能够很好地吻合,淤泥土层虽离散性较大,用HS模型也能得到预期的效果。HS模型除可以模拟硬土之外,对于模拟软土也具有有效性。
2)采用均匀设计表法有效减少了参数反演分析中刚度参数取值次数和数值模拟分析次数,计算结果表明将均匀设计法和有限元数值模拟计算相结合的参数反演分析方法在岩土工程领域具有合理性。
